一种基于GNSS的站内列车精确定位方法

马梓尧,王海峰,2,齐志华,张启鹤,范 宇

(1.北京交通大学电子信息工程学院,北京 100044； 2.北京交通大学轨道交通运行控制系统国家工程研究中心,北京 100044； 3.中国铁道科学研究院集团有限公司通信信号研究所,北京 100081)

引言

列车定位是列车运行控制系统的关键技术，高精度的列车位置信息和准确的轨道占用信息对列车在区间内安全运行和车站内进行越行、交会或调车作业至关重要。目前广泛采用应答器方式对列车进行定位，采用轨道电路的方式进行列车轨道占用检查，而这两种方式需要的大量地面设备带来了建设成本高、维护困难等问题[1-2]。

近年来发展迅速的卫星定位技术因其实时、高精度、全天候等特性开始得到各行业的关注与应用[3]。将卫星定位技术应用于列车定位领域，可以减少轨旁设备，降低列车安全运行的成本[4]。美国GE公司开发的ITCS增强型列车运行控制系统于2006年正式应用于我国青藏铁路。该系统主要以全球导航定位系统(Global Navigation Satellite System， GNSS)为主，轨道电子地图为辅，通过无线网络实现车地通信技术，依据虚拟闭塞控制方式实现列车定位[5]。

在基于GNSS定位的技术方法方面，文献[6]将列车高速行驶时卫星信号所产生的多普勒频移引入GNSS接收机提高信号捕获搜索效率，同时应用GNSS/惯导/航位推算系统的组合定位的方式来处理卫星信号中断的情况；文献[7-8]分别应用BDS/里程计和BDS/GSM-R组合定位的方式，对各传感器观测信息融合解算来降低传感器误差结果的影响。基于GNSS的列车定位方法中，确定列车所占用的轨道区段是关键环节，文献[9，10]在列车车头和车尾分别安装卫星定位接收机，通过分析卫星定位解算过程，利用列车车头与车尾的最不利位置来确定列车在区间的轨道占用；文献[11]利用贝叶斯估计法，给出了平行股道场景下的列车占用股道的决策方法，降低了传统的方法容易受到粗大误差的影响；文献[12]将列车的位置估计建模为一个完整的二维姿态估计过程，而文献[13-14]利用轨道区段的拓扑结构,将列车位置估计简化为一个一维纵向列车位置估计和一个轨道区段占用识别的结合。上述研究聚焦于列车在区间的轨道占用识别或者列车位于平行股道单一场景下的占用识别，没有考虑列车在站内咽喉区复杂场景下的位置决策问题。同时由于铁路车站线路、环境复杂，GNSS卫星信号的质量在传输过程中会受到天气的变化、建筑物和移动体遮挡的影响[15-16]，给基于GNSS列车站内定位带来了更大的困难。

为解决上述问题，本文提出了一种定位方法，首先使用直线轨段而不是传统的轨道区段来对车站铁路线路进行划分，并利用直线轨段的拓扑关系和一维信息构建电子地图；其次用随机模型描述列车的位置信息，通过贝叶斯推断计算GNSS测量值下列车位于不同直线轨段的后验概率，来确定列车所占用的直线轨段，并构建卡尔曼滤波器将速度测量值和位置测量值结合，以此来提高定位的精确性和稳定性。

1 基于GNSS的站内列车定位分析

1.1 站内列车定位的特殊性

车站是办理铁路客运、货运业务以及运输组织作业的主要场所，在铁路运输中承担了除列车在区间运行以外的各项转运作业。铁路车站在咽喉区都会布置较多的道岔，且在站内设计到发线、调车线、牵出线和货物线等多种线路来满足种类复杂的作业需求。基于GNSS的站内列车定位具有以下特殊性。

(1)列车通过道岔后将改变运行线路，如果采用传统的轨道区段来划分车站轨道网络，当列车占用道岔轨道区段时，将无法区分列车走行的是直股或是弯股。

(2)车站内轨道密集，间距较近，由于GNSS接收机的精度限制，如果只通过将距GNSS测量值最近的点确定为列车位置估计点，会出现列车估计位置在不同轨道区段间变化的情况。

(3)车站自身及周围的建筑物会对GNSS的卫星信号造成不良影响，将会降低列车定位的精度。

1.2 站内列车定位方案

根据基于GNSS的站内列车定位特点，提出的站内列车定位示意如图1所示。

图1 基于GNSS的站内列车定位示意

基于GNSS的站内列车定位的流程如图2所示。

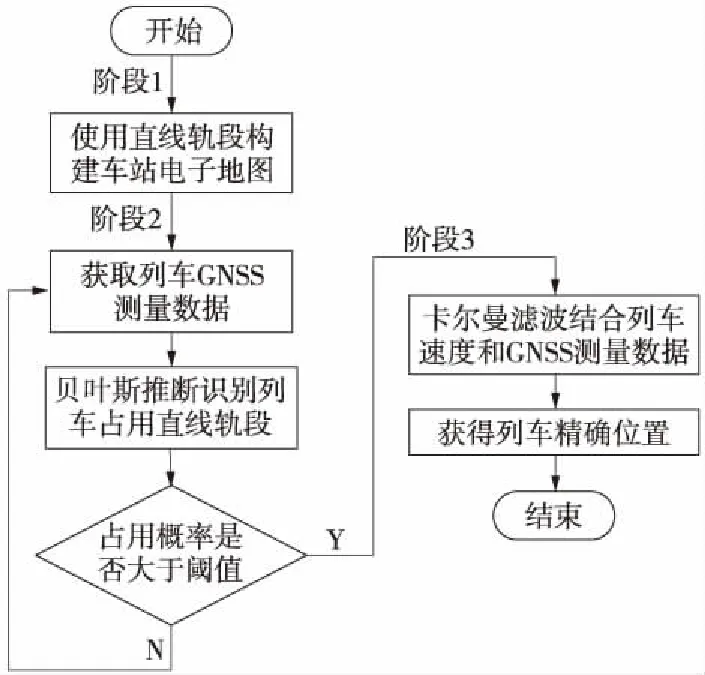
图2 基于GNSS的站内列车定位流程

在图2的阶段1中，由于传统道岔区段无法区分列车通过道岔后的走行方向，以直线轨段为基本要素,来更进一步地刻画站场不同形式轨道区段和道岔区段的轨道网络拓扑结构。如图1中以直线轨段T1，T2和T3对道岔轨道区段进行进一步的划分。在图2的阶段2中，因为站内咽喉区道岔和直线轨段数量多，GNSS定位数据存在误差，直接将距GNSS定位数据最近的直线轨段确定为列车占用的轨段准确率较低。因此，使用贝叶斯推断对列车短时间内多个GNSS定位数据进行迭代计算，来确定列车所占用的直线轨段。在图2的阶段3中，由于GNSS信号会受车站自身及周围建筑物的影响，利用卡尔曼滤波器结合速度传感器和GNSS接收机的测量值，提高GNSS接收机的信号受扰时的列车定位精度。

2 基于直线轨段的车站线路电子地图设计

在基于GNSS的列车定位中，电子地图是实现定位的基础，利用直线轨段的地理信息及它们之间的拓扑关系来构建电子地图。

使用包含轨道结点和连接结点的图来模拟车站轨道网络的拓扑关系。一个图G=(V，E)由结点集V和边集E组成，每条边是一个有序或无序对(v，w)，其中v，w∈V。G中每个结点都有自己的度数，结点的度指的是该结点上边的数目[17-18]。

直线轨段表示一段直线轨道或者一段曲率半径很大的曲线轨道，并且任意直线轨段都不包含道岔，轨道结点是直线轨段的模型。

与轨道结点相连的是连接结点，利用结点的度数来区分3种不同的连接结点。

(1)一度连接结点：与轨道结点之间只有一条边相连，作为轨道末端或地图边界端点的模型。

(2)二度连接结点：与不同的两个轨道结点之间各有一条边相连，作为两个相邻轨道结点之间的连接点的模型。对于一段较长的，曲率半径较小的无岔轨道区段，可以用多个二度连接结点划分多个直线轨段。

(3)三度连接结点：与不同的3个轨道结点之间各有一条边相连，作为道岔的模型。

每个轨道结点都有两个端点，每一个连接结点有一个端点。若轨道结点和连接结点存在相同的端点ID，则代表这两个结点之间有一条边相连，以此来表示站场轨道网络的拓扑关系。从车站站场图到轨道电子地图拓扑关系的转换如图3示意。

图3 站场图与电子地图转换

GNSS接收器以WGS-84坐标提供大地位置[19]，采用这种坐标来描述车站电子地图中轨道的特征点。如图4所示。

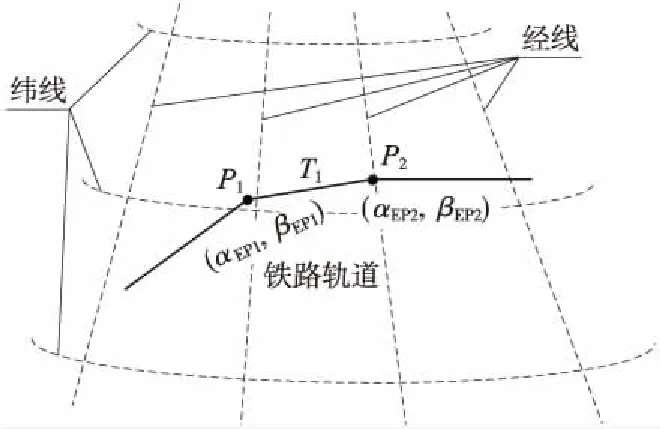
图4 在WGS-84坐标下的轨道

图中，αEP1和αEP2分别代表直线轨段端点P1和端点P2的经度，βEP1和βEP2分别代表直线轨段端点P1和端点P2的纬度。

此外，通过“直线轨段+偏移量”的方式来描述直线轨段上任意一点的位置。如图5所示，端点P1设为始端端点，将直线轨段上任意一点D1到始端端点的距离称为偏移量l。

图5 直线轨段上的偏移量

3 基于贝叶斯推断的列车位置识别

3.1 直线轨段占用识别方法

列车位置和运动的描述需要知道列车当前所在的直线轨段、沿着直线轨段的位置和列车速度。对于站内轨道线路，尤其是咽喉区，由于道岔和直线轨段的数量多，GNSS定位数据存在误差，不易快速、准确地选出占用的直线轨段，列车的运动状态存在很大的不确定性。由此推导出一种随机模型来描述列车的运动状态。

随机变量T、L和V分别代表列车所处的直线轨段tk、列车车头在直线轨段上的偏移量l和列车的速度v。其中速度v是一个有符号标量，v为正(负)号表示列车是向前(或向后)行驶的。假设随机变量T满足分类分布，并且在确定列车占用的直线轨段为tk的条件下，车头的偏移量与速度满足二元高斯分布。可以用一组假设来描述当前列车的位置，如式(1)所示。

P(T，L，V)=P(L，V|T)·P(T)

(1)

式中，P为某事件发生的概率；T为列车占用的直线轨段；L为列车车头在直线轨段上的偏移量；V为列车的速度。

基于列车状态的随机模型，可以使用贝叶斯推断来估计列车直线轨段的占用情况。在车载GNSS接收机尚未开始输出定位信息时，假定列车在每个直线轨段上的概率都是相等的，也就是说若站内有n个直线轨段，则列车占用直线轨段tk的概率值都为1/n，称此概率值P(tk)为先验概率。在获得GNSS接收机的位置测量数据gm后，可通过后验概率P(tk|gm)来估计列车所占用直线轨段tk的不确定性。通过贝叶斯公式融合每一次接收机的测量数据，来把先验概率转化为后验概率。

使用贝叶斯公式可以将P(tk|gm)转化为式(2)。

(2)

式中，

gm=(α，β)

(3)

其中，α为GNSS接收机的经度测量值，β为GNSS接收机的纬度测量值。考虑到在tk上的任意位置的偏移量l，有

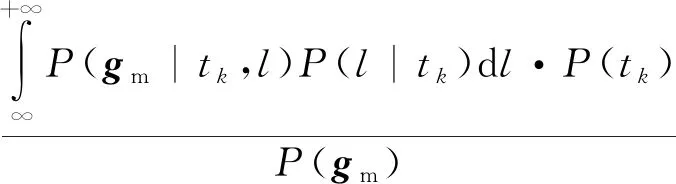
(4)

式中，∝为正比符号，说明了后验概率正比于一个积分项乘以先验概率P(tk)。

在式(5)中，首先考虑先验概率P(tk)这一项。以1%为阈值，在每次GNSS测量后，删除后验概率小于此阈值的直线轨段占用假设。

直线轨段上的任意位置都应该有相对应的坐标gt。将坐标周围局部的地球表面用过点的切平面来近似，则可以得到直线轨段上偏移量为l处的坐标，见公式(6)。

(6)

式中，(αEP1，βEP1)，(αEP2，βEP2)为直线轨段的两个端点的坐标；lEP1和lEP2为两端点的偏移量。

假设GNSS的测量值服从二元高斯分布，协方差矩阵记为∑g。因为接收机提供无偏的、随机独立的测量值，若列车车头位于直线轨段tk，偏移量为l，则此时车头位置的GNSS测量值均值应为

μgm=gt

(7)

式(7)表明列车GNSS测量值的均值都位于tk上，积分项可以写成

(8)

式中，μl和σl分别是列车占用tk条件下，车头偏移量l分布的均值与方差。

用式(5)中积分项与先验概率的乘积结果来表示后验概率的大小，其中积分项可以看作关于参数tk的函数，但并不是tk的概率分布，也就是说在所有不同tk条件下，各个积分项求和的值并不等于1。在计算完所有直线轨段的后验概率值后，要对这些值进行归一化处理，最终将概率值低于1%的直线轨段占用假设删除。每得到一个GNSS测量就进行一次计算，直到最后只剩一个直线轨段占用假设，则就认为此直线轨段即为列车占用的直线轨段。

3.2 直线轨段占用更新方法

在确认了列车占用的直线轨段后，还需要确认列车在直线轨段所处的位置。利用GNSS测量值gm到列车占用的直线轨段tk的垂直投影点gp来估计列车的位置。

垂直投影点gp与GNSS测量值点gm的关系如式(9)所示。

gp=kd+(αEP1，βEP2)

(9)

式中，

d=(αEP2-αEP1，βEP2-βEP1)

(10)

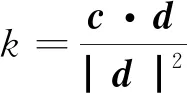
(11)

c=gm-(αEP1，βEP1)

(12)

式中，(αEP1，βEP1)，(αEP2，βEP2)为直线轨段的两个端点的坐标； 由式(6)和式(9)可得GNSS测量值点gm与列车车头在轨道段上的偏移量l的关系如式(13)所示。

l=k(lEP2-lEP1)+lEP1

(13)

式中，lEP1和lEP2为直线轨段两端点的偏移量。

列车在实际的站场内运行时，一旦列车车头的偏移量l超过直线轨道区范围，就必须进行列车从一个直线轨段到另一个直线轨段的占用更新。如图6所示，设列车车头初始位于直线轨段T1上的D1处。如果列车车头下一时刻运行到D1处，列车车头在T1上的偏移量l′超出了T1的范围，那么必须更新占用的直线轨段。

图6 列车直线轨段占用更新

3.3 通过道岔的处理方法

于列车自身无法确定道岔处于定位或反位，在通过道岔时会重新遇到确定直线轨段占用的问题。

列车通过一个单开道岔时有对向和顺向两种情况。列车对向通过道岔时，根据道岔开通的方向，列车有可能驶入直股或弯股。但列车顺向通过道岔时，列车只有一个行驶方向。

在第一种情况下，由于列车无法确定自身将驶入的是哪个直线轨段，将再次使用贝叶斯推断来进行直线轨段占用识别。而在第二种情况下，就不需要再次进行列车直线轨段占用的识别，以此来提高系统的实时性。

通过对电子地图中的轨道结点增加标记的方法来区分这两种情况。将与三度连接结点相连，表示直股和弯股的直线轨段的两个轨道结点标记为0，另一个轨道结点标记为1。由此，便可用两相邻的直线轨段标记之和是否>0来区分列车通过道岔的情况。

如图7(a)是交叉渡线道岔的平面布置图。在图7(b)电子地图中4组道岔都表示为三度连接结点，T2、T5、T7和T8对于4组道岔来说都是表示直股或弯股的直线轨段，均标记为0。列车通过交叉渡线任意一组道岔的处理方法均与列车通过一个单开道岔相同。例如列车从T3对向通过道岔C2驶向T2或T7，将产生这两个直线轨段的占用假设。

图7 交叉渡线

复式交分道岔可以用来缩短车站咽喉长度、减少车道用地、提高调车作业效率。复式交分道岔的平面布置如图8(a)所示。

图8 复式交分道岔

复式交分道岔平面布置图中1/3和5/7是双动道岔，其中1和7是可动辙叉。按照图8(b)的方式来构建轨道电子地图。用单开道岔C1来表示5/7，用C2来表示1/3，同时添加直线轨段T2。在图8(a)中列车由A驶向B相当于图8(b)中列车由T1驶向T3。由于在实际定位过程中并没有直线轨段T2，因此令T2的长度L2为0。若列车于T1经过道岔C1驶向T3或T6，如果没有添加T2，则会面临列车此时占用的直线轨段T1和T3、T6的标记都为0，造成无法产生新的占用假设的情况。在添加了T2后，列车顺向通过C1后，直线轨段占用变为T2。又由于T2的长度L2是0，则占用随之变为与之相连的C2的T3或T6。

站场内还有一些轨道连接会导致某一直线轨段的标记既可以是1又可以是0。如图9(b)，对于C1来说T2的标记应该为0，而对C2来说T2的标记应该为1。

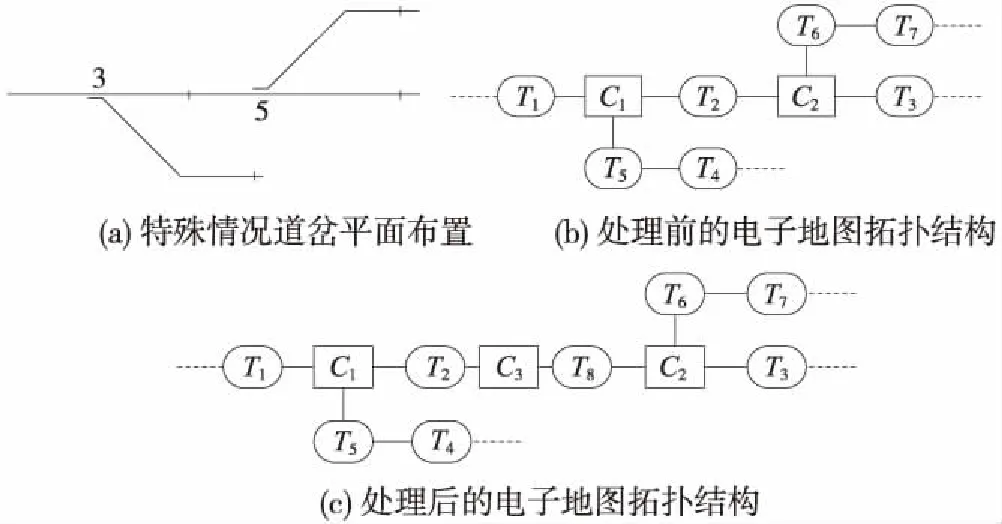
图9 特殊道岔处理情况

通过添加一个二度连接结点来避免这种情况。结果如图9(c)所示，此时T2的标记为0，Tg的标记为1。

4 基于卡尔曼滤波的列车位置误差校正

在传统列车定位方法中，一般使用GNSS测量值对列车占用的直线轨段的投影点作为列车的位置估计。但GNSS信号不良会导致对列车的位置估计误差增大。用列车所占用的直线轨段，列车车头在所占用直线轨段上的偏移量l和列车速度v这3个变量来表示列车的状态，并推导出一个交替执行预测和更新步骤的卡尔曼滤波器来估计列车状态，以此来校正GNSS信号较差的情况下带来的位置误差。

假设列车所占用的直线轨段的长度L1接近无限长，列车以恒定的速度v行驶。在这个假设中，列车的状态随时间的变化可以用式(14)和式(15)表示。

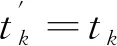
(14)

(15)

由于式(15)具有线性特征，可以用卡尔曼滤波预测步骤来预测状态[20-21]，记为式(16)的形式

P′=APAT

(16)

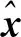
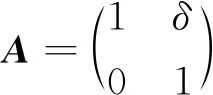
(17)

使用GNSS接收机的位置测量值和速度传感器的速度测量值来修正预测值。GNSS接收机提供列车车头的坐标测量值gm，速度传感器提供列车的速度测量值vm。

由式(6)知，GNSS测量值在直线轨段上的投影gP与速度传感器测量值vm同列车的状态变量l和v之间的关系可以用式(18)来表示。

(18)

式中，ε为GNSS接收机和速度传感器的测量误差，服从高斯分布；(αEP1，βEP1)，(αEP2，βEP2)为直线轨段的两个端点的坐标；lEP1和lEP2为两端点的偏移量。e如式(19)所示。

(19)

根据式(18)可以使用一个标准的卡尔曼滤波器更新步骤来将测量值结合到位置估计中，以此来得到列车车头在所占用直线轨段上的偏移量l的最优估计。

使用卡尔曼滤波器估计列车车头位置，每次新的位置估计值都是基于上一次的位置估计值。因此需要对一周期只考虑一次位置估计值的直线轨段占用更新方法进行相应修改。

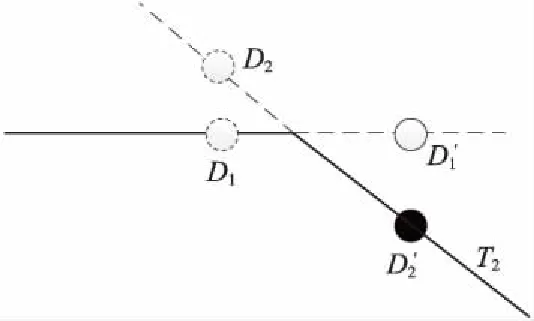
图10 修改后的直线轨段占用更新

5 实验分析

5.1 测试参数及环境

在某车站完成了数据采集，利用MATLAB对采集到的数据进行了仿真分析。车站共有39组道岔，并设有牵出线、货物线和安全线等线路。

位置数据采集使用的GNSS接收机为LAND-PAK系列GPS单点定位接收机，定位精度2.0 m(CEP)；速度数据采集使用的是DSH 16涡流速度传感器，脉冲计数误差为±1。速度传感器的测速精度与计数脉冲频率，也就是与列车速度有关，为了便于计算，速度测量值的标准差σvm的值统一定为0.05。

假设接收机的测量误差服从高斯分布，且测量数据是无偏的，同时认为测量值gm的经度和纬度测量值是独立的。CEP的定义为式(20)所示。

CEP=0.59(σα+σβ)

(20)

式中，σα为接收机经度测量值的标准差；σβ为接收机经度测量值的标准差。

根据接收机的参数，同时由于接收机测量值gm的经度和纬度测量值是独立的，可以假设σα的值与σβ相同。由式(20)可计算得接收机经、纬度测量值的标准差如式(21)。

σα=σβ=1.69

(21)

5.2 直线轨段占用识别结果分析

列车以20，40，60，80 km/h和100 km/h 的速度分别对向通过站内不同的39组道岔，接收机通过10Hz的频率进行GPS数据采集。实验结果表明：在5种速度下通过不同的39组道岔都正确地识别出了列车占用的直线轨段，同时还记录了驶过每组道岔到正确识别直线轨段占用列车所行驶的距离，结果如图11所示。

图11 列车速度对直线轨段占用识别的影响

由图11可知，列车在不同速度下通过39组道岔，随着列车速度的增加，完成直线轨段占用判断时列车所行驶的距离也在增加。但是所有的实验都在列车行驶55 m以内完成了直线轨段占用判断，并且绝大部分实验在列车行驶35 m以内就完成了直线轨段占用判断。

文献[22]利用基于多假设的垂直投影地图匹配方法进行列车的轨道占用识别。与本文方法类似的是，基于多假设的垂直投影法同样需要对列车短时间内多个GNSS测量点进行迭代计算来确认列车占用的轨道。为进一步验证本文提出方法的先进性，将列车以上述5种不同速度通过39组道岔的GPS数据使用垂直投影法进行直线轨段占用识别。用列车驶过每组道岔到正确识别直线轨段占用所行驶距离的长短来表示两种方法的实时性。垂直投影法与本文方法的比较结果如图12所示。

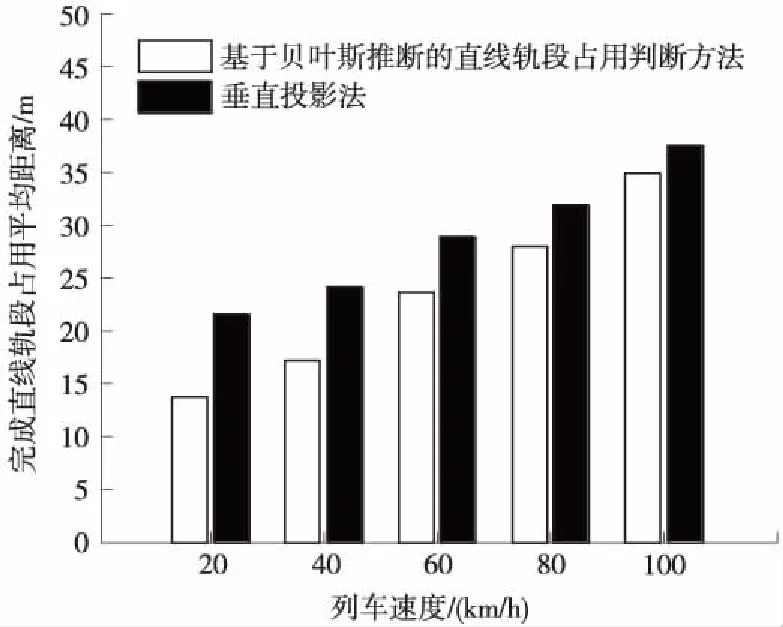
图12 本文方法与垂直投影法对直线轨段占用识别实时性对比

图12表示了两种不同方法在不同速度下完成直线轨段占用列车行驶距离的情况。垂直投影法在不同速度下行驶的平均距离为28.4 m，而基于贝叶斯推断的直线轨段占用识别方法在不同速度下行驶的平均距离为23.4 m，也就是说，本文方法较垂直投影法的实时性提升了17.6%。

5.3 列车位置误差校正结果分析

列车在长度为850 m的直线轨段上以30 km/h的速度匀速行驶，接收机通过1Hz的频率进行GPS定位数据采集。通过式(17)和式(18)分别确定卡尔曼滤波的状态转移矩阵和观测矩阵，并根据接收机和速度传感器测量值的标准差确定测量协方差矩阵。图13显示了卡尔曼滤波前后列车车头偏移量误差的对比。

图13 卡尔曼滤波前后列车车头偏移量误差对比

图13(a)结果显示了列车车头偏移量的估计值与实际值始终存在一个5 m内的偏差。图13(b)显示了在使用了卡尔曼滤波后，列车车头偏移量估计值与实际值偏差逐步缩小到1 m以内。

6 结论

本文引入贝叶斯推断和卡尔曼滤波理论，提出了一种基于GNSS的站内列车定位方法。给出了一种以直线轨段为基本要素精确刻画复杂铁路站场不同形式轨道区段拓扑结构的方法。基于拓扑描述，贝叶斯推断方法，进一步给出了站内直线轨段占用识别方法，结合卡尔曼滤波解决了传统方法轨道区段占用识别实时性较低和列车位置估计容易受到GNSS信号波动影响的问题。同时，针对列车站内运行的特点，推导了铁路车站咽喉区列车运行轨段动态更新方法。

利用实际车站列车行车的GNSS采集数据进行仿真实验，结果表明，所提出的基于贝叶斯推断的直线轨段占用识别方法的实时性较现阶段被广泛使用的垂直投影方法提升了17.6%，通过引入卡尔曼滤波将列车的GNSS信息和速度信息进行融合，将一般性能的GNSS接收机2～3 m的位置估计误差降低至1 m以内。本文提出的方法可效降低GNSS信号不稳定情况下的定位误差，提升列车定位的稳定性和精确性，可为行车指挥及列车运行智能化管理提供可信的定位支撑。