高速铁路无砟轨道扣件弹条疲劳损伤统计分析

刘玉涛,段玉振,王 豪,亓 伟

(1.中铁第四勘察设计院集团有限公司,武汉 430063； 2.铁路轨道安全服役湖北省重点实验室,武汉 430063；3.西南交通大学,成都 610031； 4.北京城建设计发展集团股份有限公司,北京 100037； 5.济南轨道交通集团有限公司,济南 250101； 6.成都工业职业技术学院现代轨道交通应用技术研究中心,成都 610218)

扣件作为钢轨与轨下结构连接的纽带，其作用十分重要。高速铁路无砟轨道扣件多依靠弹条将钢轨扣压于轨道板或道床板。线路运营过程中，列车通过会对扣件弹条造成疲劳损伤，损伤积累到一定程度则会引起扣件弹条折断。弹条疲劳损伤的大小受列车轴重、行车速度、轨道不平顺、扣件预压力和弹条材料强度等因素影响[1]，而且这些影响因素都具有较强的随机性，这使得扣件弹条的疲劳损伤也具有较强的随机性。对弹条疲劳损伤的随机性展开研究有助于工务部门制定扣件系统养护维修计划，其意义十分重大。

针对扣件弹条折断问题，国内外学者主要从材料及加工工艺和动、静态受力两方面进行了研究。扣件弹条的材料和加工工艺方面，郭和平[2]等对60Si2MnA材料弹条进行断口微观观察、金相组织检测和材料成分检测等，认为弹条折断主要由原材料的碳含量偏低导致热处理后材料硬度偏低引起。李天夫[3]采用相同的方法，认为弹条的原材料盘条在热轧过程中发生折叠，折叠处引起应力集中，导致弹条发生早期疲劳断裂。张彦文[4]等研究发现扣件扭力矩超标、使用环境含有腐蚀性介质会加剧弹条的疲劳折断。弹条动、静态受力方面，肖俊恒[5]等研究了高速铁路钢轨波磨和车轮多边形磨耗引起的轮轨高频振动，认为轮轨高频激励与扣件弹条固有频率接近时弹条产生共振，从而造成弹条疲劳断裂。陈宪麦[6]、肖宏[7]、高晓刚[8-9]等对地铁DTⅥ2型弹条、e型弹条、PR单趾弹条和高速铁路ω型弹条的模态特征、频响特性进行分析，认为轮轨激振频率与弹条的固有频率一致引发共振，是导致弹条疲劳断裂的主要原因。向俊[10]等对扣件安装、车轮多边形磨耗及曲线线型等条件下的扣件弹条力学特征进行分析，研究了不同条件下弹条断裂原因。余自若[11]等建立了扣件系统精细化有限元模型，将竖向位移施加于绝缘垫块，研究了不同扣压力和载荷频率下弹条的疲劳损伤。凌亮[12]、尚红霞[13]等研究了钢轨波磨下弹条的动力响应，分析了弹条断裂的原因并提出减小弹条振动和疲劳断裂的建议。刘小军[14]对焊缝不平顺激励下弹条动应力及其疲劳寿命进行了研究。亓伟[15]等对客货混运线路扣件弹条疲劳特性进行了准静态分析。侯尧花[16]等采用基于声振互易的试验方法对铁路扣件弹条模态进行了研究。崔树坤[17]、刘晓丹[18]等对高速铁路用WJ-8型扣件弹条和Ⅱ型弹条的模态特征进行了试验研究。徐启喆[19]等对扣件系统组合失效对钢轨参数的影响进行了研究。邓士豪[20]等提出基于边界约束刚度参数优化的轨道扣件弹条防断裂设计方法。

综上所述，当前的研究主要集中在特殊地段扣件弹条断裂的原因分析方面，如钢轨波磨地段、焊缝附近及潮湿隧道内，针对扣件弹条疲劳损伤随机性的研究较少，本文考虑不平顺、扣件螺栓预压力以及弹条材料强度随机性的影响，以单元双块式无砟轨道WJ-8型扣件弹条为例，采用数值仿真和概率统计的方法对其展开研究。

1 扣件弹条疲劳损伤计算方法

为了对高速铁路无砟轨道扣件弹条疲劳损伤进行计算和统计分析，采用如图1所示的分析方法。首先，建立车辆-轨道耦合系统动力学模型，用于计算轨道高低随机不平顺激励下钢轨与道床板间的相对位移；其次，结合扣件弹条危险区域应力大小与上述相对位移之间的关系，得出扣件弹条的应力变化时程曲线；最后，采用雨流计数法，得出弹条应力循环幅值与均值，并进行疲劳损伤计算与统计分析。

图1 分析流程

WJ-8型扣件弹条由60Si2MnA材质的弹簧钢制作而成，该材料的σ-N曲线如公式(1)所示。

lgN=39.595 3-11.843 6lgSa

(1)

式中，Sa为应力循环幅值，MPa；N为试件破坏时的应力循环次数。

由于扣件弹条是在螺栓预压力下工作的，其内部存在较大的初始应力。为了得到扣件弹条在螺栓预压力下的初始应力，建立WJ-8型扣件系统精细化模型，如图2所示。约束铁垫板支座与绝缘垫块底部节点自由度，并在螺栓垫片顶部节点施加垂直向下的压力以模拟扣件安装时螺栓预压力，得到螺栓预压力下扣件弹条的应力云图如图3所示。由图3可知，弹条中肢与弹条旁肢体圆弧连接处应力较大，该位置弹条处于弯矩、扭矩和剪力作用下的复杂受力状态，弹条断裂也多发生在此处，该位置为扣件弹条的危险区域，该处弹条最大Von-Mises应力为1 580 MPa。

图2 扣件系统有限元模型

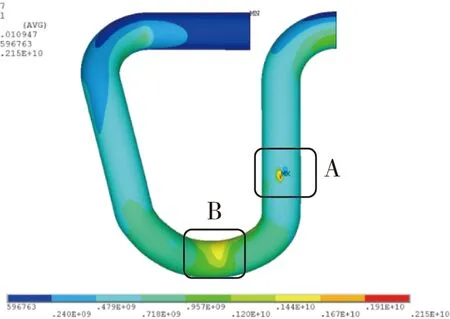
图3 弹条Von-Mises应力云图

完成扣件安装过程的计算后，固定螺栓垫片顶部节点所有自由度，释放绝缘垫块底部节点垂向自由度，并竖直向下移动绝缘垫块，以模拟列车经过时钢轨向下移动的过程，得到弹条危险区域Von-Mises应力与钢轨与道床板间相对位移的关系式如式(2)所示。由式(2)可知，弹条危险区域Von-Mises应力与钢轨与道床板间相对位移存在162.8 MPa/mm的线性关系。

y=1 580+162.8x

(2)

式中，y为弹条危险区域Von-Mises应力最大值，MPa；x为钢轨相对道床板位移，mm。

为考虑螺栓预压力随机性的影响，假设弹条危险区域初始应力服从正态分布，正态分布的均值为1 580 MPa，标准差为15.8 MPa。采用Goodman公式消除初始应力的影响，如式(3)所示。

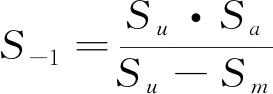
(3)

式中，Sa为循环应力幅值；Sm为应力循环均值；S-1为相同寿命下平均应力为零时的应力幅值；Su为材料的极限强度，考虑不同扣件弹条材料极限强度的随机性，假设弹条极限强度服从正态分布，正态分布均值为1 700 MPa，标准差为8.5 MPa。

将Goodman公式修正后的应力循环幅值S-1，代入式(1)中计算循环次数N。定义构件在应力水平Si作用下经受ni次循环的疲劳损伤为D=ni/Ni。在k个应力水平Si作用下，各经受了ni次循环，则可定义其总损伤为

(4)

2 计算模型及相关参数

建立如图4所示的车辆-轨道垂向耦合系统动力学模型，模型主要由车辆系统、轮轨接触和轨道系统组成。为了考虑相邻车辆依次通过对弹条疲劳损伤的影响，车辆系统采用4车编组的多刚体模型，轮对、车体和构架都简化为刚体，轮对保留沉浮、侧滚自由度，车体和构架保留沉浮、点头和侧滚自由度；一系悬挂和二系悬挂都简化为垂向的刚度与阻尼。轮轨接触刚度采用线性赫兹接触刚度。

图4 列车-轨道垂向耦合系统动力学模型

采用单元双块式无砟轨道，模型相关参数见表1。

表1 轨道相关参数

模型中钢轨采Euler梁模拟，道床板和支承层采用弹性薄板单元模拟。扣件与路基简化为垂向的刚度与阻尼。约束钢轨的纵横向位移，只保留垂向位移及相应转动自由度，约束轨道板的纵横向位移，保留垂向位移及相应转动自由度。轨道高低不平顺采用由我国高速铁路无砟轨道不平顺谱反演得到的不平顺时域样本，如图5所示。

图5 轨道高低不平顺谱

3 扣件弹条疲劳损伤统计分析

对于单元双块式无砟轨道，道床板在伸缩缝处断开，使得道床刚度在板端与板中有所不同。为了考虑道床刚度差异性对扣件弹条疲劳损伤的影响，按照车辆运行方向将扣件分为板端扣件、板中扣件和板尾扣件，如图4所示。提取轨道不平顺区段内100块道床板上板端、板中和板尾扣件各100组弹条的疲劳损伤结果如图6所示。

图6 板端、板中与板尾扣件弹条疲劳损伤

从图6中可以看出，在轨道随机不平顺激励下扣件弹条疲劳损伤具有较强的随机性，一节车厢造成的扣件弹条疲劳损伤主要集中在1.0×10-6以下，最大为2.5×10-6。为了研究扣件弹条疲劳损伤的概率分布特性，首先需要确定其服从的概率分布。为此，作扣件弹条疲劳损伤数据经验分布函数与指定分布函数之间的关系曲线图，即P-P图，以检验疲劳损伤数据是否服从指定的分布。图7～图9分别是板端、板中和板尾扣件弹条疲劳损伤数据的经验分布函数与对数正态分布的分布函数图。从图中可以看出，除了个别点外，疲劳损伤数据都在一条直线附近，因此扣件弹条疲劳损伤近似服从对数正态分布。另外，采用单样本Kolmogorov-Smirnov法进行概率分布检验，结果表明疲劳损伤在显著水平0.05下服从对数正态分布，该分布的概率密度函数和数学期望、方差分别如式(5)～式(7)所示。

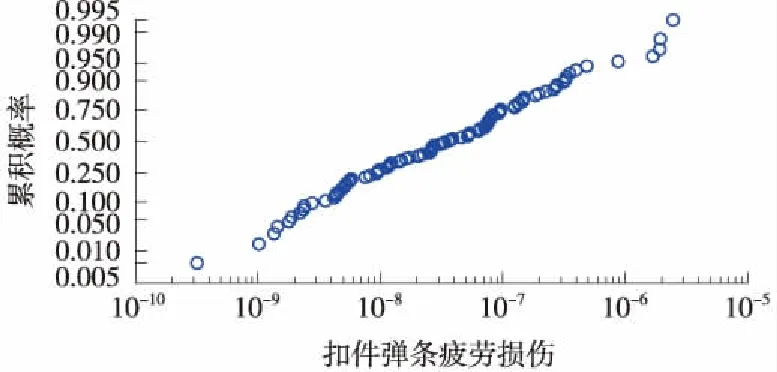
图7 板端扣件弹条疲劳损伤对数正态概率

图8 板中扣件弹条疲劳损伤对数正态概率

图9 板尾扣件弹条疲劳损伤对数正态概率

概率密度函数

(5)

数学期望

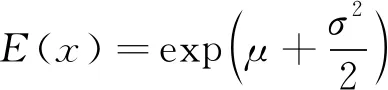
(6)

方差

D(x)=exp(2μ+σ2)(exp(σ2)-1)

(7)

为了获取概率分布的统计特征，采用对数正态分布概率密度函数对扣件弹条疲劳损伤数据进行拟合，得到弹条疲劳损伤的频率直方图与对数正态分布概率密度曲线如图10所示，数学期望、方差及其置信区间见表2。

由图10可知，采用对数正态分布概率密度函数对弹条疲劳损伤数据进行拟合，取得了较好的拟合效果。对比道床板不同位置扣件弹条疲劳损伤的统计特征可以看出，板端与板尾扣件弹条疲劳损伤的数学期望分别是1.73×10-7和1.99×10-7，方差分别是7.75×10-13和1.44×10-12，两者的数学期望与方差都相差不大；板中扣件的数学期望和方差较板端与板尾扣件大，数学期望为板端与板尾扣件的2.1～2.4倍，方差为板端与板尾扣件的7.7～14.2倍。因此，道床板不同位置的扣件弹条疲劳损伤相比，板端与板尾扣件弹条的疲劳损伤相差不大，板中扣件较板端与板尾扣件大，并且离散性也相对较大。

对所有疲劳损伤数据进行拟合，结果表明：4车编组通过造成的扣件弹条疲劳损伤服从数学期望为2.44×10-7，方差为2.39×10-12的对数正态分布，数学期望95%的置信区间为[1.50×10-7，4.26×10-7]，方差95%的置信区间为[5.24×10-13，1.45×10-11]。

图10 频率直方图和理论对数正态概率密度函数

表2 道床板不同位置处扣件弹条疲劳损伤统计特征

4 不同通过轴重下弹条折断概率分析

上述计算中列车轴重为17 t，4车编组的通过轴重为272 t，假定前后经过的列车造成的扣件弹条损伤互不影响，根据中心极限定理，大量列车经过造成疲劳损伤的标准化变量近似服从标准正态分布。由此得到不同通过轴重下弹条的折断概率如图11所示。

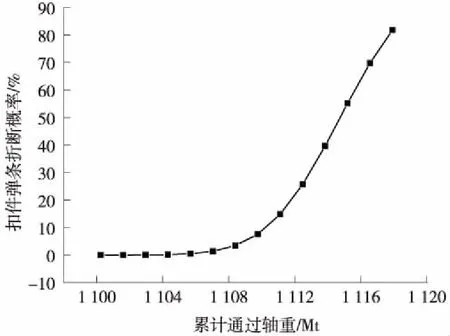
图11 不同通过轴重下扣件弹条折断概率

由图11可以看出，累计通过轴重1 100 Mt以下，扣件弹条折断概率很小，当累计通过轴重大于1 106 Mt时，随着通过轴重的增加，扣件弹条的折断概率大幅增加。因此，高速铁路WJ-8型扣件弹条在累计通过轴重1 100 Mt以下具有极高的可靠性，建议累计通过1 100 Mt前将扣件弹条全部更换。

5 结论

为了研究高速铁路无砟轨道扣件弹条疲劳损伤的统计特性，考虑不平顺、扣件预压力及弹条材料强度的随机性的影响，建立了车辆-轨道耦合系统动力学模型，计算了单元式道床板不同位置处扣件弹条的疲劳伤损并对其进行统计分析，得到如下结论。

(1)单元式道床板不同位置处扣件弹条疲劳损伤都服从对数正态分布，板端与板尾扣件弹条疲劳损伤的数学期望和方差都相差不大，板中扣件的数学期望约为板端与板尾扣件的2.1～2.4倍，方差为板端与板尾扣件的7.7～14.2倍。

(2)总体而言，4车编组通过造成的扣件损伤服从期望为2.44×10-7，方差为2.39×10-12的对数正态分布，数学期望95%的置信区间为[1.50×10-7，4.26×10-7]，方差95%的置信区间为[5.24×10-13，1.45×10-11]。

(3)高速铁路WJ-8型扣件弹条在累计通过轴重1 100 Mt以下具有极高的可靠性，建议在累计通过1 100 Mt前将扣件弹条全部更换。

本文只对长度约为600 m的轨道不平顺区域内板端、板中和板尾扣件弹条的疲劳损伤进行了计算与统计分析，下一步应延长不平顺区域长度，以消除轨道不平顺非平稳性的影响。另外，本文中只考虑了扣件螺栓预压力和弹条材料强度的随机性，还需考虑列车轴重、行车速度等随机性的影响。