风-光-抽水蓄能联合发电系统的优化运行

杨森,张青，高立艾

(河北农业大学 机电工程学院,河北 保定 071001)

当今社会,科学技术、工业水平和生活质量得到了飞速的发展,不免过度依赖于一次能源.能源的不合理使用导致环境污染和能源匮乏问题日益凸显.可再生能源如风能、太阳能、水能等二次能源,得到了世界各国的广泛关注[1-3].风力发电、光伏发电和储能装置联合运行的并网技术日渐成熟,优化其运行成了不可避免且至关重要的课题.因为风力资源和光资源在自然界中具有不确定性,所以如果运用不当,就会出现严重的弃风弃光现象.在风电和光伏发电系统中,将抽水蓄能系统作为一种特殊的储能装置,可以与其合理配合,在系统调峰过程中缓解电网压力,提高风电、光伏的消纳水平[4-6].

文献[7]建立了抽水蓄能-风力和光伏电站联合发电的数学模型,对联合发电系统进行了出力特性分析和功率预测,采用多变异自适应遗传算法优化抽水蓄能电站的出力值,但是计算过程中稳定性有所欠缺.文献[8]提出了同时动态调整学习因子和惯性权重的粒子群算法,对风-光-抽水蓄能联合发电模型进行求解,但在采用惩罚函数来处理约束条件时,对惩罚因子的选取有些困难.文献[9]通过风-光-抽水蓄能的联合运行,使系统的综合出力更好地适应负荷特性,提高风电、光伏消纳能力,并建立了联合优化模型,但是只介绍了系统出力跟随负载曲线,没有考虑到联合发电系统的经济效益.文献[10]构建了风-光-抽水蓄能联合发电系统模型,提出了一种基于电力市场环境下的联合运行方法,但是采用的改进遗传算法精度较低,联合发电系统的出力优化不够精确,寻优能力较弱.文献[11]提出基于改进万有引力搜索算法,解决微网中多约束优化问题,但是算法的运行时间比较长,需要的参数较多.

本文通过改进粒子群万有引力算法,引入混沌算法与惯性权重，并改进步长因子,在风-光-抽水蓄能联合发电系统的基础上,以经济效益最大化为目标建立数学模型,优化联合发电系统出力,得出联合发电系统最佳出力值.

1 联合发电系统

1.1 联合发电系统结构

图1 联合发电系统Fig.1 structure of co-generation system

风力发电和光伏发电因受风能和光能资源的影响,具有很强的波动性和季节性.在风、光资源充足时,如果不合理调配,不仅很容易导致资源的浪费,还会因为波动性对电网造成损失.在用电低峰期时,光伏和风力发电系统发出的电能一部分用于并网和负载使用,另一部分带动主厂房的水泵将下水库的水抽到上水库,将多余电能转化为势能储存起来;在用电高峰期时,光伏和风力发电系统发出的电不够负载使用,蓄能电站将上水库的水引向下水库,将势能转化为电能.联合发电系统结构如图1所示.抽水蓄能电站作为储能系统,就是实现在势能和电能之间转化,间接将风光发电系统的剩余电量储存起来,实现能源利用率最大化.

1.2 联合发电系统数学模型

1.2.1目标函数

以联合发电系统的经济效益最大化为目标,建立目标函数.目标函数为

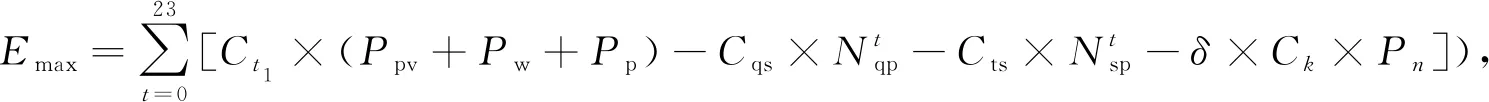
(1)

上述目标函数中,在最高效利用资源的同时,寻求风-光-抽水蓄能的最佳出力情况,使得联合发电系统的收益最大化.

1.2.2约束条件

出力偏差约束为

(1-α)Pplan≤Ppv+Pw+Pp≤(1+α)Pplan，

(2)

式中,α为系统运行过程中,相对于Pplan允许的最大偏差.

上、下水库水量平衡约束[12]为

(3)

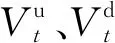
(4)

式中，Qt为t时刻水站流量;ηtc为t时刻抽水效率.

fd(Pp,Hst)表示抽水蓄能发电功率Pp和水头Hst,该时刻下因发电流到下水库的水量，关系式为

(5)

式中，Qt为t时刻水站流量;ηtf为t时刻的发电效率.

水库库容约束

(6)

一天循环首末时刻水量差约束

φmin≤V24-V0≤φmax.

(7)

输出功率平衡约束

(8)

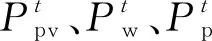
风电场、光伏电站输出功率约束

(9)

抽水蓄能机组功率约束

(10)

2 算法介绍

2.1 粒子群万有引力混合算法(PSOGSA)

万有引力搜索算法(gravitational search algorithm,GSA)[13]是2009年第1次由Esmat等提出.传统GSA算法运行过程中缺乏一定的记忆性和群体交流，在位置更新时,当前粒子仅对目前迭代中的位置起作用,对其他的粒子没有信息共享的能力,进而就会出现算法早熟、容易陷入局部最优的现象.为了防止万有引力搜索算法的弊端出现,引入粒子群算法.

粒子群算法中,对于个体而言,不仅每个个体都具有记忆性,而且每个个体都保存了自己搜索到的最优信息;对于整个群体而言,群体则会保留目前迭代状态下群体最优信息.将粒子群算法的优点与万有引力搜索算法相结合,可以充分克服GSA算法早熟、容易陷入局部最优的不足.

粒子群万有引力算法(particle swarm optimization and gravitational search algorithm,PSOGSA)[14]中个体的速度和位置更新公式为

(11)

(12)

2.2 改进粒子群万有引力混合算法(IPSOGSA)

2.2.1更新初始位置

算法初期,所有粒子的初始位置是随机的,有可能出现粒子分布稠密不均而导致算法收敛速度变慢,进而陷入局部最优.为解决此问题,引入混沌理论算法来进行初始化,混沌理论算法

y(n+1)=4y3(n)-3y(n)，

(13)

式中,y(n)∈(-1,1),且y(n)≠0.

初始化的方法:在H维空间里的Z个粒子个体,先随机产生第1个H维向量y1的个体,再利用式(13)对y1进行Z-1次迭代,产生Z-1个个体,取值为[-1,1]，

(14)

式中,xij为目标种群里粒子i在j维度上的值；xfmax、xfmin分别表示为个体取值的上、下限；yij表示混沌算法下粒子i在j维度上的值.

2.2.2引入惯性权重

在原始PSOGAS算法里,位置更新时,局部与全局之间作用没有明显的界限;迭代后期,随着个体间的距离变小,引力也随之增大,就会在局部或者全局极值附近出现振荡现象,导致无法稳定在最优值位置.引入惯性权重ω′,可以很好地平衡全局探索能力和局部开发能力，即

(15)

式中,fi为第i个粒子的适应度值；fmax、fmin分别为最优个体和最差个体适应度值.故改进后位置更新公式为

图2 算法流程Fig.2 Flow chart of algorithm

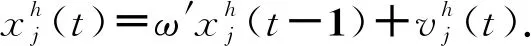
(16)

2.2.3改进步长因子

由文献[15]可知,gbest加入到速度矢量中会削弱寻优能力.文献[15]对c1、c2处理时,前期的自适应程度较低,所以对c1、c2进行以下修正：

(17)

式中,a是迭代数,A是最大迭代数.

2.2.4算法步骤

1)初始化混合算法参数.初始化算法种群数量、迭代数等参数,用混沌理论初始化粒子的位置;

2)计算初始适应度值.根据式(1)计算初始位置下各粒子的适应度值;

3)更新步长因子和速度.根据当前迭代数,采用式(17)更新c1、c2,并代入式(11)计算当前各粒子速度;

4)更新粒子位置.找出最优个体和最差个体适应度值,进而以式(15)和(16)更新种群中每个粒子的位置;

5)更新适应度值.将更新位置的粒子以式(1)为适应度函数,计算当前迭代数下各粒子新的适应度值;

6)检验是否达到最优条件.判断算法迭代数是否达到最大,或者连续若干次最优值是否保持不变,若满足,则停止搜索,否则转向3).

算法流程如图2所示.

3 算例分析与实验结果

图3 分时上网电价Fig.3 Time-of-use feed-in tariff

联合发电系统及算法初始化数据设置如下:最大迭代T=1000次，维数n=3，种群规模Z=600;风电场、光伏电站的装机容量分别为3000、1000MW,抽水蓄能机组为4×300MW;设置出力偏差在Pplan的5%;发电效率0.8;抽水效率0.938;抽水蓄能单机启、停成本2000元/次;惩罚系数δ=1.5;抽水蓄能的水头/扬程为311m;抽水蓄能上、下库总库容分别为4.38×107m3、3.764×107m3;上、下水库调节库容为2.7755×107m3;一天0:00上水库蓄水为2.0×107m3,首末时刻库容差5×106m3.根据电力市场分时上网电价设定参考电价,如图3所示.

采用IPSOGSA算法优化风-光-抽水蓄能联合发电系统,计算得出联合系统各系统出力值、抽水蓄能启停台数和算法迭代数,结果见表1.计算得出总经济效益,并分别与PSO、GSA、PSOGSA算法比较分析.

在实际工程算例当中,人为设定19:00至次日7:00没有光照,光伏出力为0.

表1 IPSOGSA优化后联合发电系统出力结果

抽水蓄能出力的数值为负值,表示抽水蓄能输出功率,蓄能电站处于发电状态,工作方式为上水库的水流向下水库,将势能转化为电能,风、光联合出力高于电网计划出力;数值为正值时,状态与负值相反.

一天当中,20:00时,风电场出力达到峰值2 773 MW,同时抽水蓄能出力相对较高,达到902 MW,这是因为一天当中达到了风力最大值,抽水蓄能电站由上水库向下水库放水量加大,说明此时进入了用电高峰期,负载达到了峰值,风-光-抽水蓄能共同向大电网输电,风光联合发电系统低于电网计划出力;0:00时，抽水蓄能出力达到负峰值910 MW,此时用电负荷较少,此时主要依靠大电网供电,但是因天气原因,风电场出力较多时,多余电量在蓄能电站转化为势能,使得抽水蓄能电站出力较大.

在4种算法情况下,联合系统出力与计划出力对比如图4所示.由图4可知,联合系统在IPSOGSA算法下,更接近出力计划,精度最大,波动性最小,偏差也最小.

图4 4种算法下联合系统出力与计划出力对比Fig. 4 Comparison of joint system output and planned output under four algorithms

优化后,根据式(1)得出：风-光-抽水蓄能联合发电系统在一天的总收益为1 079.4万元,PSO、GSA、PSOGSA分别得到的总收益为891.3、949.7、991.9万元;IPSOGSA算法迭代在500～605次,PSO、GSA、PSOGSA迭代数分别为900～975、775～850、650～750.由于篇幅限制,本文以11:00时为例,分别对比4种算法下的迭代数和收益即适应度值,对比结果如图5所示.

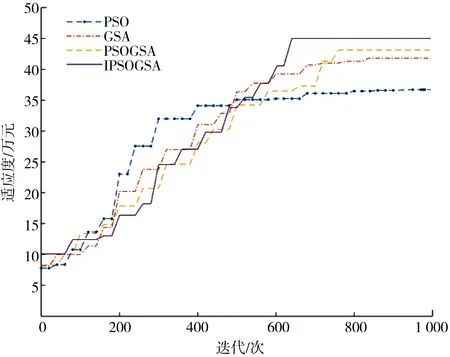
图5 11：00时不同算法适应度对比Fig.5 Fitness comparison of different algorithms at 11:00

由此可以得出,利润方面本文算法IPSOGSA能够更高于PSO、GSA、PSOGSA算法,是由于迭代过程中,粒子位置更新时改进了步长因子,令步长因子采用自适应值,使得算法在探索与开发2个阶段逐步过渡,粒子向最优解加速,在计算精度方面更具有优势.在算法初期引入混沌算法初始化粒子位置,使初始粒子分布均匀,便于算法在寻优过程中更好地把握初始粒子位置,加快了收敛速度,使得迭代数更少,可以充分满足工程需要.此外,加入惯性权重,各部分出力优化过程中避免出现“出力振荡”的现象.

综上所述,通过改进的粒子群万有引力算法(IPSOGSA)迭代次少、寻优能力和稳定性强,应用此算法优化后的联合发电系统经济效益最大.

4 结 论

本文在粒子群万有引力混合算法基础上,引入混沌算法，加入惯性权重并改变步长因子,提高了算法的寻优能力,通过算例验证了其优越性;将改进的算法应用于优化对风-光-抽水蓄能联合发电系统的出力,通过对比计划出力曲线与4种算法下的出力曲线、在同一时刻条件下不同算法的迭代数与经济效益,IPSOGSA算法更接近计划出力曲线,达到的利润高于其他算法所计算出的利润,并且迭代数更少.