管壳式换热器优化的遗传算法及变量分析

何 璟，张永恒，王良璧

(1. 兰州交通大学 化学与生物工程学院，兰州 730070；2. 兰州交通大学 新能源与动力工程学院，兰州 730070； 3. 兰州交通大学 铁道车辆热工教育部重点实验室，兰州 730070；4. 兰州交通大学 机电工程学院，兰州 730070)

管壳式换热器具有结构简单、造价低廉、适应高温、高压能力强，是最常用的一类换热器[1]，广泛应用于石油、化工、核电、制药、食品等工业领域，其作用是将热流体的部分热量传递给冷流体[2].

传统换热器设计一般没有将换热器的运行费用作为考量参数，无法达到一次性投入与经济收益的最优化.考虑运行费用和投资费用的优化主要有细菌觅食算法(BFA)、遗传基因算法[4](GA)、帝国主义竞争算法(ICA)、基于生物地理学的优化(BBO)、粒子群算法(PSO)，人工蜂群算法(ABC)、布谷鸟搜索算法(CSA)、引力搜索算法(GSA)、萤火虫算法(FFA)等[3-7].这些研究方法的优化目标是使换热器的总费用最低[8-10]，总费用包含了换热器初始投资费用和运行过程中需要克服流体阻力而消耗的动力费用.

本文通过遗传基因算法对管壳式换热器以总费用最低作为目标函数进行了优化.并分析了管束排布方式、管径、管心距、管长、管数、折流板切割率、折流板间距等设计变量对换热器传热有效度、总费用的影响.

1 管壳式换热器热力计算方法

管壳式换热器壳程传热和阻力计算模型有贝尔-台华(Bell Delaware)法、克恩(Kern)法等[11].管程是直管管束，传热系数和压降的计算采用管内强制对流[12]的计算公式，壳程用Bell-Delaware法计算传热系数及压降[12].弓形折流板几何参数计算见[13-14]，壳体直径计算见[15]：

1.1 管程测传热系数和压降的计算

管程传热系数ht采用Dittus-Boelter公式：

(1)

式中：λt为管程流体导热系数，W/(m·K)；di为管内径，m；Pr为管程流体普朗特数；Ret为管程流体雷诺数；mt为管程流体质量流量，kg/s；μtw为管内壁温对应的管程流体动力粘度，Pa·s.

管程压降的计算采用McAdams公式：

(2)

式中:L为换热长度，m；ρt为管程流体密度，kg/m3；ut为管程流体流速，m/s；摩擦系数f为：f=0.004 6

(Ret)-0.2.

1.2 壳程传热与压降修正

壳程传热系数hs：

hs=hidJcJIJbJsJr.

(3)

式中：折流板切口和跨距校正因子Jc；壳体对折流板的泄漏、管程对折流板的泄漏的影响校正因子Jl；管束流路和流路旁路的影响Jb；进出口折流板不等间距的影响Js；层流时负传热温差校正因子Jr.

理想管束纯横流下壳程传热膜系数hid:

(4)

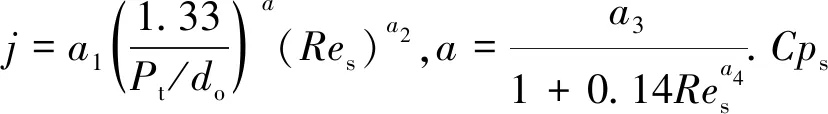
壳程总压降ΔPs由折流板缺口区总压降ΔPwi、中间段横流总压降ΔPcr和进出口受旁路影响的压降ΔPio组成：

ΔPs=ΔPwi+ΔPcr+ΔPio,

(5)

ΔPwi=

(6)

ΔPcr=(Nb-1)ΔPbidζbζl,

(7)

(8)

2 换热器优化设计数学模型

2.1 目标函数

以换热器系统的总成本最小作为优化设计目标.总成本TC包括换热器投资费用IC、管内、管外流体的阻力损失成本OC.目标函数模型：

TC=IC-OC.

(9)

在管壳式换热器设计中,为使设计的换热器在经济上最优，考虑以下费用：

1) 设备投资费用：

管程、壳程流体材料假设为不锈钢，设备投资费用采用[16]中公式计算.

IC=8 500+409A0.85.

(10)

式中：A为传热面积，m2.

2) 操作费用：

泵的运行操作费用OC是由于克服管内和管外流体的阻力损失而产生的动力消耗[7].

(11)

Co=P·op·ec,

(12)

(13)

式中：mtΔPt/ρt、msΔPs/ρs分别为管程、壳程功率损失，Pa；ΔPt、ΔPs分别为管程、壳程阻力损失，Pa；mt、ms分别为管程、壳程介质流量，kg/s；ρt、ρs分别为管程、壳程介质密度，kg/m3；设备寿命ny取10年；年折现率i为10%；年操作小时op取7 500小时/年；电费ec为0.15美元/千瓦时；泵效率η为0.6.

2.2 传热有效度和传热单元数

在进行换热器设计时，为了取得最经济的制造成本又满足传热的工艺要求，需要对传热流体的流向安排、传热面积、和传热系数对设计的影响定性分析.常常采用传热有效度和传热单元数的方法.传热有效度ε等于实际可传递的热量与理论上可能传递的热量之比，对于1-2n型换热器[12]：

(14)

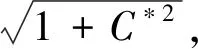
mh、mc分别为热、冷流体的质量流速，kg/s；Cph、Cpc分别为热、冷流体的定压比热容，J/(kg·℃).K为传热系数，W/(m2·℃).

3 计算实例及分析

3.1 遗传基因算法

遗传算法(Genetic Algorithm，简称GA)是一种将生物进化引入到数学模型中来的随机搜索算法，在复杂系统的优化方面有着广泛的应用.遗传算法首先从随机产生的一组初始种群开始，通过个体竞争，自然选择，杂交等方式进行的“适者生存”的进化过程生成子代种群，子代个体经过变异“优胜劣汰”，使个体的适应性能力不但增强，通过不断的进化，直至最后搜索到满意解为止.选择、交叉和变异是遗传算法的三种主要操作，分别模拟了自然界的生物的繁衍、交配和基因突变.

根据管壳式换热器主要优化参数的分析，将管径、管间距、管束排布方式、管长、管数、折流板间距、折流板缺口7种参数作为遗传算法中的个体.在选择操作中，某一个体能够继续存在于下一代的概率与其适应度有关.在每一代中，适应度较低的一部分个体被选择操作去除，同时生成相等数量的新个体，以保持群体规模不变.本文选取进化代数是500代，种群规模为100.

交叉操作是在随机选取的两个染色体之间通过交换其相同基因位完成的.这一操作是否进行由交叉概率决定.本文在计算中交叉概率选为0.75.

变异操作是对待优参数进行精细修正的一种技术.它由变异概率控制，本文中采用标准变异操作(每一个基因都进行相同的变化)和小的变异概率0.005.

3.2 设计变量的选取

管径、管间距、管束排布方式、管长、管数、折流板间距、折流板缺口等7种参数作为管壳式换热器遗传算法中的个体，构成设计变量，它们的取值及范围为：

换热管径do：根据换热管标准，选取二十种不同规格的管径，如表1所列.

换热管中心距Pt：通常用换热管外径来表示，选择有1.25do，1.50do两种；

管束排布方式β：换热管的布置由管束间的夹角确定，如图1.按标准有30°，45°，90°三种；

换热管管长L：选取3～6m.

换热管管数Nt：选取100～600根.

折流板间距Lbc：折流板间距取值范围较大，最佳值为20～140%壳体内径；

折流板切割率Bc：选择范围为10～45%壳体内径进行计算.

3.3 计算实例

算例来源于Shah[12]的文献，表2是原始数据和操作条件.

表1 换热管规格(do,di) (单位：Inch)

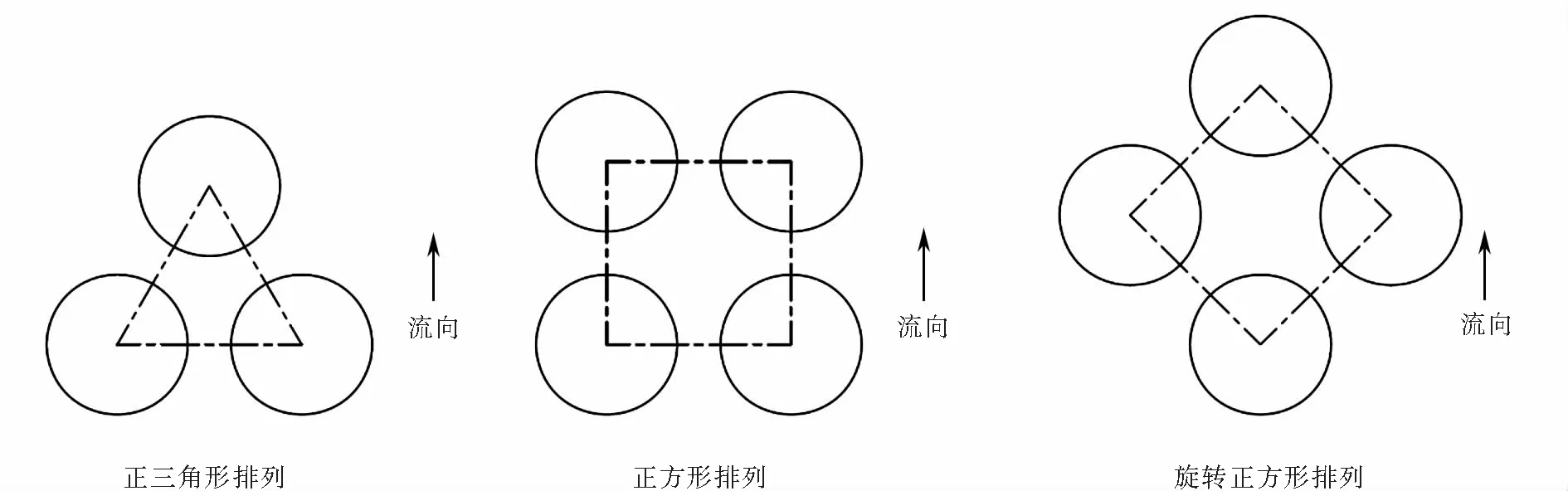
图1 管束排布方式Fig.1 Layout of the tube bundle

表2 算例原始数据和操作条件

3.4 计算结果

表3是算例的文献计算结果与本文优化结果对比.由表3可以看出，未优化前的换热器总费用73 893.25$，优化后明显降低.但也发现，优化后的传热有效度由0.155 5降低到0.093 5，降低了40%.

由图2(a)可以看出，投资费用与排布方式无关，这是由于投资费用只与换热器面积有关.30°排布时的运行费用最高，90°排布时的运行费用最低，因此30°排布时对的总费用最高，90°排布时对的总费用最低.由图2(b)可以看出，30°排布时传热有效度最高，90°排布时传热有效度次之，45°排布时传热有效度最低.

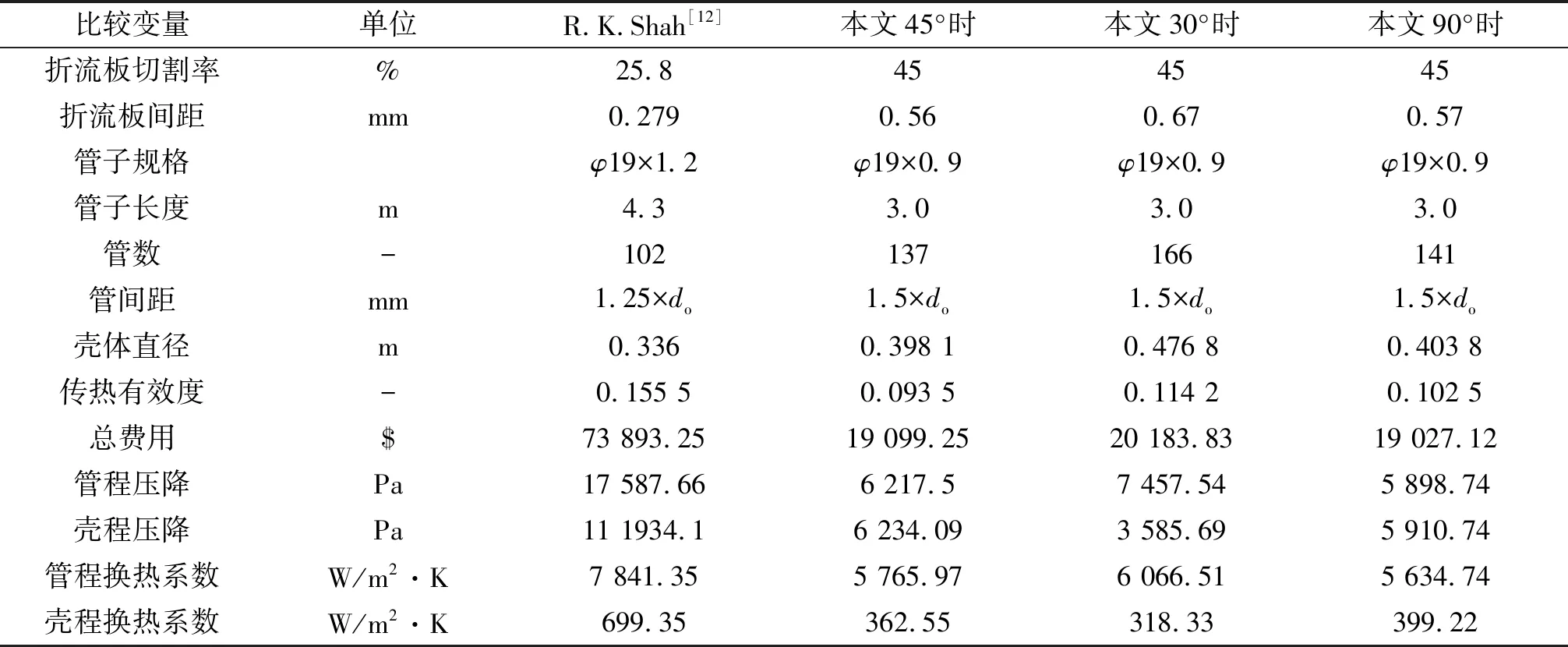
表3 本文与文献结果对比

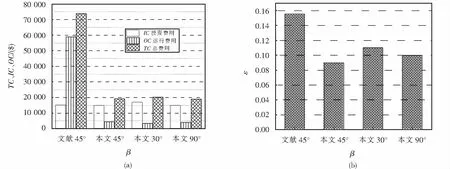
图2 不同排布角时费用(a)和有效度(b)对比Fig.2 Comparison of the cost and effectiveness under different tube bundle layout

3.5 结果分析

为了分析管束排布方式、换热管直径、管心距、管长、管数、折流板切割率、折流板间距等设计变量对传热有效度、总费用的影响，以下计算以90°排布时的数据为设计变量的初值.

3.5.1 管径对传热有效度和总费用的影响

由图3可以看出，其他设计变量不变时，排布角相同时，随着管径的增加，传热有效度增加，总费用降低.排布角不同时，30°排布时传热有效度最高，总费用也最高；90°排布的传热有效度次之，所需总费用最低，45°排布传热有效度最低，但总费用低于30°排布，高于90°排布.

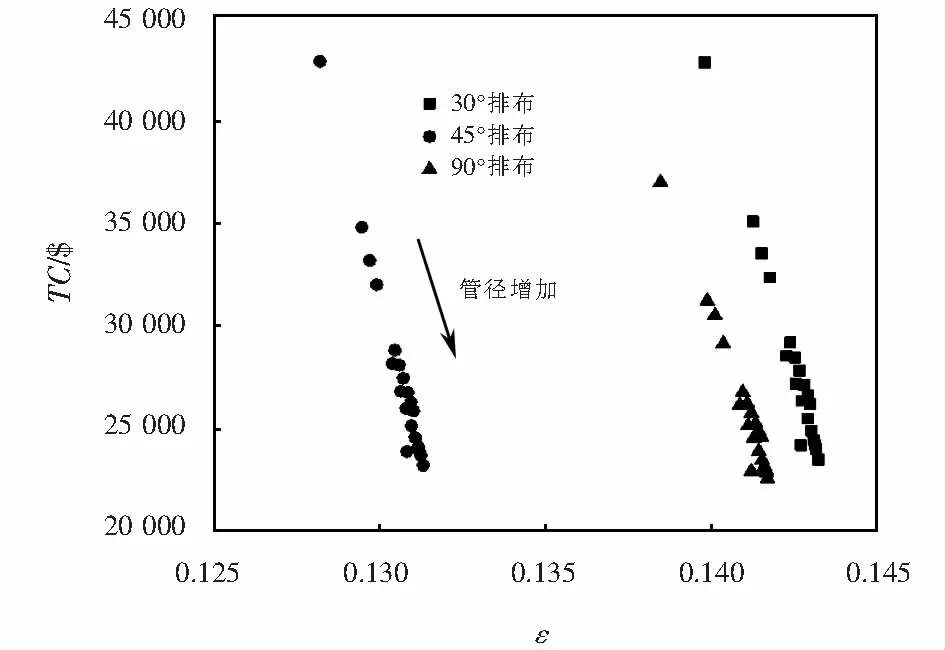
图3 管径对费用和有效度对比Fig.3 Comparison of the tube diameter to cost and effectiveness

3.5.2 管心距对传热有效度和总费用的影响

由图4可以看出，其他设计变量不变时，排布角相同时，随着管心距的增加，传热有效度先增大后减小，管心距在1.2～1.3do传热有效度最好.随着管心距的增加，换热器总费用降低.排布角不同时，管心距在1.0～1.2do时，30°排布时传热有效度最高，总费用也最高，90°排布的传热有效度次之，总费用最低，45°排布的传热有效度最低，但总费用低于30°排布，高于45°排布.管心距在大于1.3do后，管束排布方式对传热有效度和压降的影响差别不大.

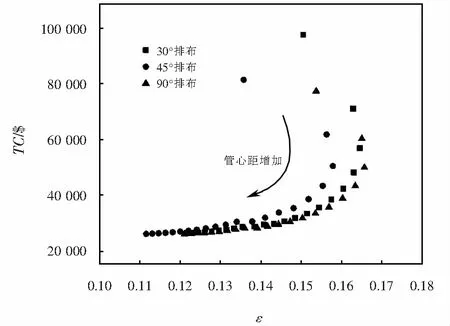
图4 管心距对费用和有效度对比Fig.4 Comparison of the tube pitch to cost and effectiveness

3.5.3 管长对传热有效度和总费用的影响

由图5可以看出，其他设计变量不变时，排布角相同时，随着管长的增加，传热有效度增加，总费用增加.排布角不同时，30°排布时传热有效度最高，总费用也最高；90°排布的传热有效度次之，所需总费用最低，45°排布传热有效度最低，但总费用低于30°排布，高于90°排布.图中曲线出现不连续阶梯的原因，是由于在计算跨折流板缺口区的有效管排数、相邻2块折流板顶端间的管排数、折流板等参数时圆整.

3.5.4 管数对传热有效度和总费用的影响

由图6可以看出，其他设计变量不变时，排布角相同时，随着管数的增加，传热有效度增加，总费用先减小后增加，存在最小值.排布角不同时，30°排布时传热有效度最高，总费用也最高；90°排布的传热有效度次之，所需总费用最低，45°排布传热有效度最低，但总费用低于30°排布，高于90°排布.

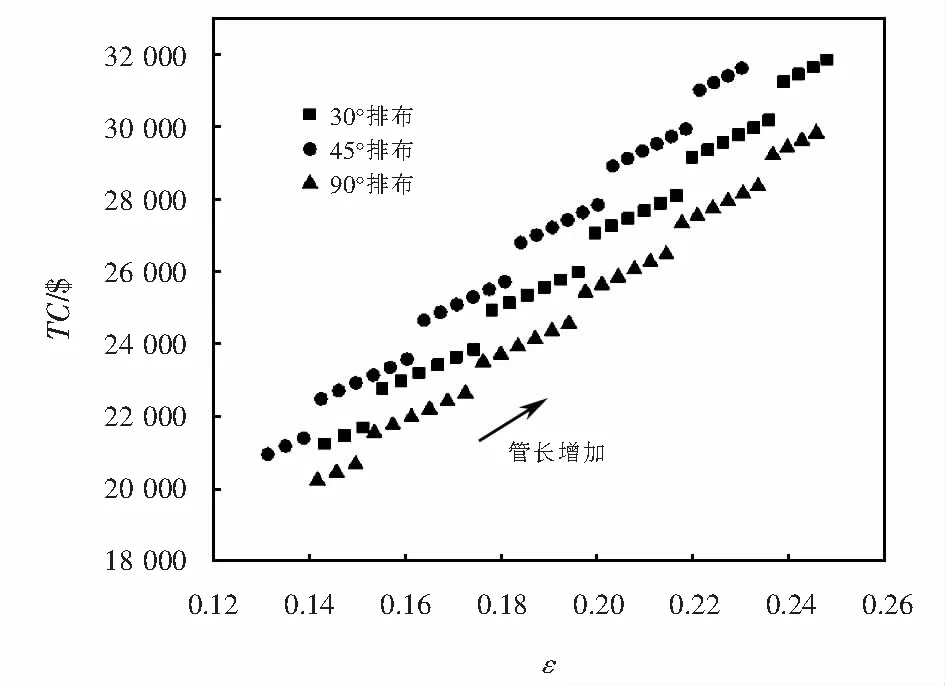
图5 管长对费用和有效度对比Fig.5 Comparison of the tube length to cost and effectiveness

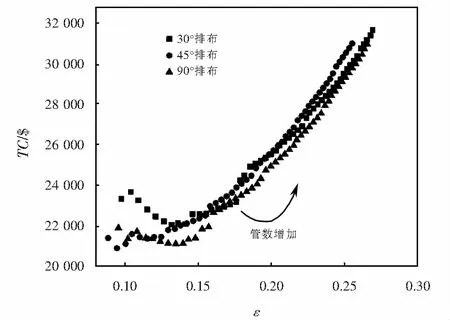
图6 管数对费用和有效度对比Fig.6 Comparison of the tube number to cost and effectiveness

3.5.5 折流板切割率对传热有效度和总费用的影响

由图7可以看出，其他设计变量不变时，排布角相同时，随着折流板切割率的增加，传热有效度降低，总费用总体降低.排布角不同时，30°排布时传热有效度最高，总费用也最高；90°排布的传热有效度次之，所需总费用最低，45°排布传热有效度最低，但总费用低于30°排布，高于90°排布.图中曲线出现局部阶梯型升高的原因，是由于在计算跨折流板缺口区的有效管排数、相邻2块折流板顶端间的管排数、折流板等参数时圆整.

3.5.6 折流板间距对传热有效度和总费用的影响

由图8可以看出，其他设计变量不变时，排布角相同时，随着折流板间距的增加，传热有效度降低，总费用总体降低.排布角不同时，30°排布时传热有效度最高，总费用也最高；90°排布的传热有效度次之，所需总费用最低，45°排布传热有效度最低，但总费用低于30°排布，高于90°排布.由图8还可以看出，在折流板间距较小时，传热有效度最高，相应的总费用也最高，在折流板间距较大时，不同管束排布方式对传热有效度、总费用的影响不大.

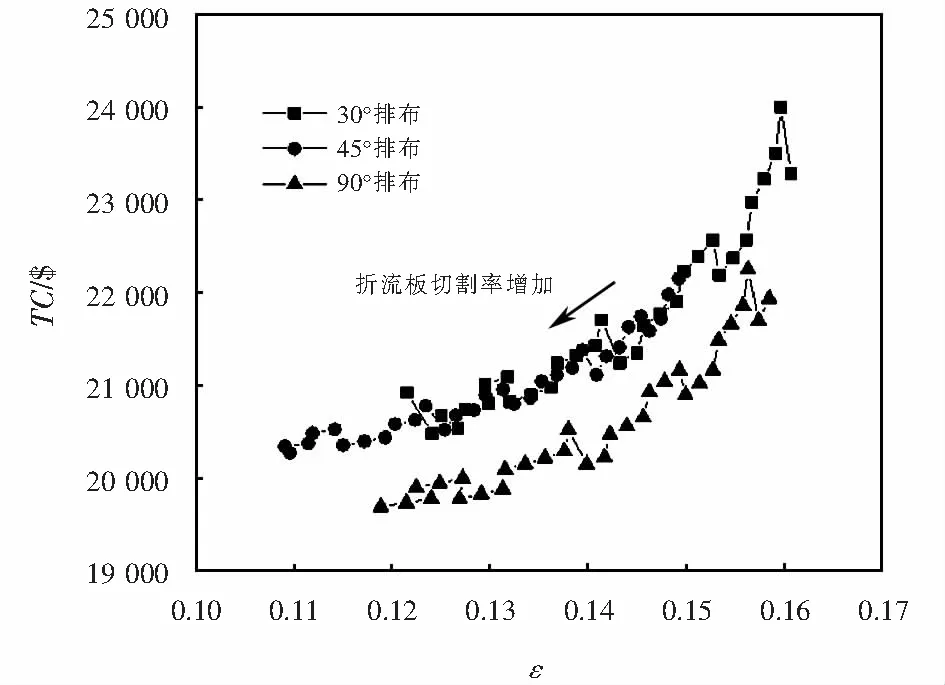
图7 折流板切割率对费用和有效度对比Fig.7 Comparison of the baffle cutting ratio to cost and effectiveness

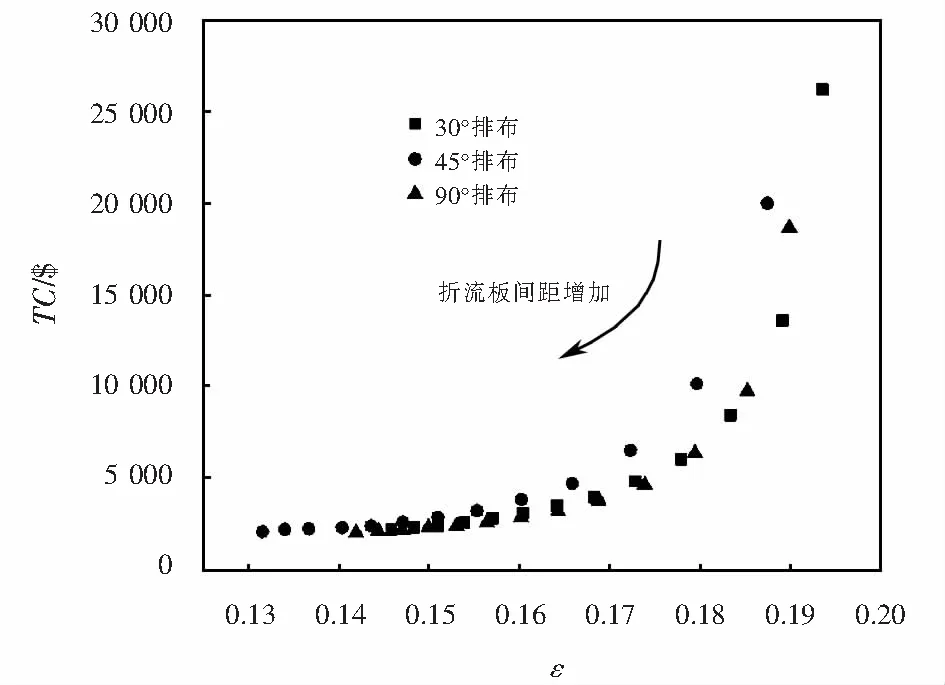
图8 折流板间距对费用和有效度对比Fig.8 Comparison of the baffle spacing to cost and effectiveness

4 结论

本文应用遗传基因算法对管壳式换热器进行优化的基础上，分析了管束排布方式、管径、管心距、管长、管数、折流板切割率、折流板间距等设计变量对换热器传热有效度、总费用的影响，结论如下：

1) 管束30°排布时传热有效度最高，总费用也最高；90°排布时的传热有效度次之，总费用最低，45°排布传热有效度最低，总费用介于30°排布，和90°排布之间.

2) 增加管径使传热有效度增加，总费用降低；增加管心距使传热有效度先增大后减小，总费用降低；增加管长使传热有效度增加，总费用增加；增加管数使传热有效度增加，总费用先降低后增大；增加折流板切割率、折流板间距使传热有效度降低，总费用降低.

3) 随着折流板间距的增加，传热有效度减小，总费用也降低.当折流板间距较大时，不同管束排布方式对传热有效度、总费用的影响不大.