一种非仿射高超声速飞行器姿态系统控制方法

路 遥，刘晓东，路坤锋

(1. 宇航智能控制技术国家级重点实验室，北京 100854；2. 北京航天自动控制研究所，北京 100854)

0 引 言

高超声速飞行器(Hypersonic flight vehicle, HFV)是指飞行马赫数大于5的飞行器，是航空工程与航天工程紧密结合的产物，具有巨大的军事和民用前景，受到世界各主要强国的关注[1]。飞行控制是HFV实现工程应用的核心问题之一。HFV具有飞行环境复杂、模型非线性程度高、强耦合以及参数不确定等特点，这使得其飞行控制器设计工作非常具有挑战性[2]。

目前HFV的常见气动布局有锥形体、升力体、翼身融合体和乘波体等。其中锥形体布局HFV于20世纪90年代被提出，具有头部尖、长细比大、弹性后掠角大、展弦比小等外形特点，较适合于用作高超声速导弹，迄今仍具有一定的研究价值[3-8]。为降低设计难度，在研究初期，很多学者通过气动分析和设定合理的假设，将HFV的数学模型描述为一类仿射型非线性系统，在此基础上基于反步法设计飞行控制器，取得了很好的控制效果。然而，HFV受到的气动力实际上与攻角、控制舵摆角等因素呈现的是非仿射关系，将其描述为仿射模型会造成一定的控制精度损失，甚至在某些情况下不能正确描述飞行器的气动特性。因此，目前对HFV非仿射模型的研究逐渐受到更多关注。文献[9]建立了HFV的速度子系统非仿射模型，并基于反步法设计了预设性能控制器。文献[10]将HFV纵向运动模型分解为非仿射形式的速度和高度两个子系统,并基于反步法分别设计了预设性能控制器；该方法不需要反复求取虚拟控制律的导数,能够有效避免反步法应用中常见的“微分膨胀问题”。文献[11]利用低通滤波器和神经网络处理和估计模型中存在的未知非仿射动态，在此基础上设计了反演控制器，提高了系统的可靠性和工程适用性。文献[12]通过分析，将HFV纵向通道模型建立为半分解非仿射模型形式，在考虑执行机构死区的情况下设计了预设性能控制器。文献[13]基于反馈线性化方法设计了HFV的鲁棒自适应模糊控制器，对于气动阻力表达式中存在的非仿射形式项，通过中值定理将其转化为仿射形式，使得飞行器模型可以描述为一种仿射形式模型。

文献[9-13]的研究中，控制输入的非线性项均存在于气动阻力表达式中，影响飞行器的速度动态而不直接影响飞行器姿态回路动态。实际上，对于某些锥形体构型HFV[14]，其控制输入的非线性项会直接影响到俯仰角速度动态，从而直接影响到飞行器的姿态稳定性。针对该类飞行器的姿态控制问题，目前的研究成果较少。文献[15]针对该类飞行器的非仿射纵向短周期姿态模型，研究了其控制输入非线性对姿态回路产生的影响，并设计了自适应滑模模糊控制器，取得了较好的控制效果。另外一些学者希望将已有的对非仿射系统的控制方法[16-19]应用于HFV，如文献[20]同样针对锥形体构型HFV的非仿射纵向短周期姿态控制问题，应用文献[18]中提出的方法进行解决，实现了对姿态回路的稳定控制。然而，文献[15]和[20]中的研究为降低设计难度，要求飞行器需处于定速定高的飞行模式，因此其控制方案的适用性受到很大限制。

本文针对HFV姿态回路非仿射模型设计一种全飞行模式适用的反演控制方法。采用干扰观测器估计攻角动态中的扰动项，得到俯仰角速度虚拟控制指令。通过扩张状态观测器估计参数未知的俯仰角速度动态函数，在此基础上基于动态逆方法设计升降襟副翼的控制律，实现对飞行器姿态的稳定控制。基于Lyapunov方法分析了闭环系统的稳定性，并通过仿真实验对其控制效果进行了验证。

1 问题描述

本文以文献[14]中给出的一类高超声速飞行器为研究对象，研究其纵向非线性模型的姿态控制问题。其模型可描述为：

(1)

式中:α,Q为分别表示攻角和俯仰角速度；γ表示航迹倾角；ΔQ表示因模型参数不确定、外部环境干扰等因素造成的干扰量；mA,mT分别表示由气动力和发动机推力产生的俯仰力矩，它们可表示为

(2)

表1 HFV的基本参数Table 1 Basic parameters of the HFV

气动系数CM,CD,CL的表达式可参见文献[15]中的附录部分。令u=δa=δe，文献[15]附录部分中的气动系数表达式在表2所示飞行状态范围内适用[14]：

表2 文献[15]中气动系数表达式成立的飞行状态范围Table 2 Ranges of the flight states within which the expressions of the aerodynamic coefficients in [15] are tenable

为方便表述，定义集合Θ表示表2所示的飞行状态范围。

本文的控制目标为：在考虑控制量可能出现饱和的情况下，设计u的控制律，使得攻角α能够准确跟踪给定的一阶导数有界的参考指令αc。为实现此目标，本文以反步法为基础，首先以俯仰角速度作为虚拟控制量，设计虚拟控制律保证攻角的跟踪性能；然后，采用动态逆的方法设计u的控制律，使得俯仰角速度能够较好地跟踪俯仰角速度虚拟控制指令。

2 控制器设计

2.1 俯仰角速度虚拟控制律设计

首先定义误差变量x1=α-αc，根据式(1)可得：

(3)

(4)

(5)

(6)

对于式(5)，以Q作为虚拟控制量，设计Q的虚拟控制律为

(7)

(8)

(9)

对于反步法应用过程中常见的虚拟控制量求导的“复杂性爆炸”问题，采用图1和式(10)所示指令滤波器解决：

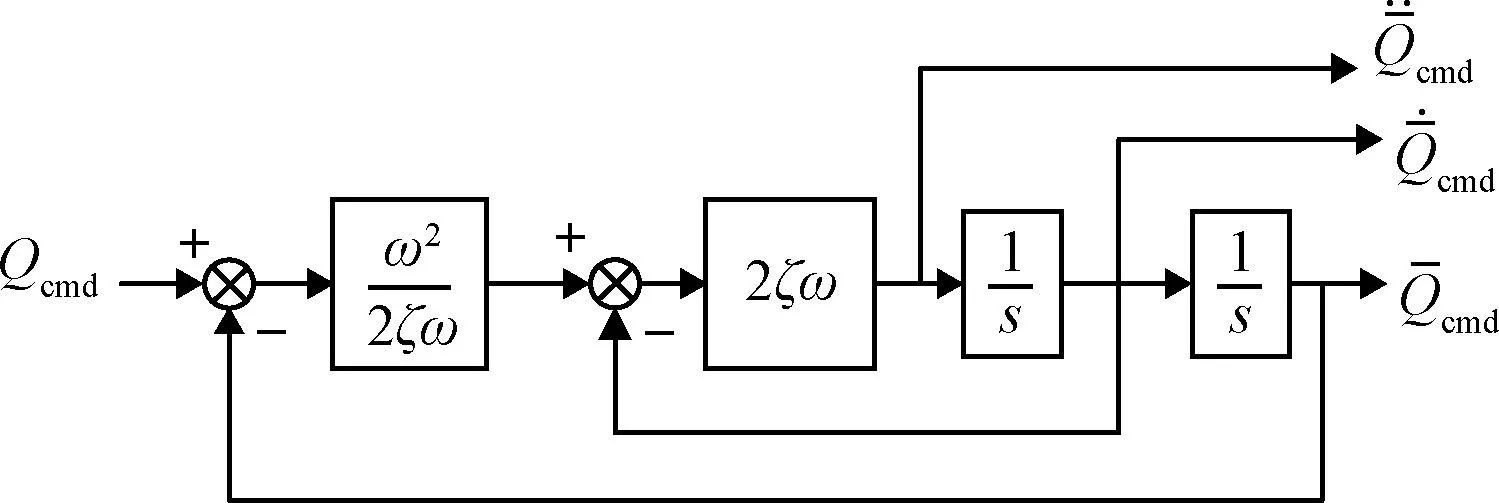
图1 指令滤波器结构图Fig.1 Structure chart of command filter

(10)

(11)

2.2 升降襟副翼控制律设计

(12)

对于误差量x2的动态，注意根据式(2)，CD的表达式中包含控制量u的二次项。文献[15]中研究了这些分量对攻角和俯仰角速度动态的影响，分析结果表明这些分量会对攻角和俯仰角速度动态产生一定的影响，且随着马赫数的增大影响越来越显著，不能简单忽略。基于此，可将x2的动态描述为：

(13)

式中:f(εi,u,ΔQ)为由式(1)和(2)确定的连续可导函数，εi为时变变量，包括：ε1=V，ε2=Ma，ε3=H，ε4=T，ε5=α，ε6=Q。ΔQ为由于气动系数不准确和外部干扰导致的扰动项。对于干扰项ΔQ和函数f(εi,u,ΔQ)，有以下假设：

假设2.[20]存在有界函数w(εj,u,ΔQ)，对于所有(α,Ma,u,H,Q)∈Θ，有：

(14)

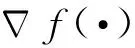
假设3.[20]当(α,Ma,u,H,Q)∈Θ时，有|∂f/∂u|>0。

注2.假设1为对于HFV俯仰角速度动态干扰项模型的常见假设，已有多个文献分析表明该假设符合HFV实际物理系统和外部飞行环境。对于假设2，本文仅考虑HFV的姿态控制问题，认为弹道飞行状态ε1,ε2,ε3是稳定的；同时考虑到HFV的发动机产生的推力大小是连续可导且有上限的，因此假设2是合理的。根据文献[20]中的相关分析可知，假设3也是符合本文选取研究对象的物理意义的。

由于f(εi,u,ΔQ)的形式比较复杂，难以直接设计u的控制律，因此首先设计如下系统的控制律：

(15)

式中:x=[x1,x2]T，u0为控制量，可设计为：

(16)

(17)

接下来，考虑设计u的控制律使得f(εi,u,ΔQ)尽可能与u0相等。由于f(εi,u,ΔQ)中存在未知量，不能直接计算，因此首先采用如下状态观测器[21]对其进行估计：

(18)

(19)

在控制律(16)、状态观测器(18)、假设3和指令滤波器输出的基础上，设计u的控制律为：

(20)

式中:k3>0为控制增益。

3 稳定性分析

(21)

对W2求导，由式(12)、(13)、(16)可得

(22)

由假设1、假设2、式(9)、(11)、(19)进一步可得：

(23)

(24)

式中:N2=N1+k3η2。根据式(21)和(24)可得：

(25)

(26)

4 仿真校验

为验证本文设计的控制方案的控制效果，分别采用本文设计的控制方案和文献[20]中提出的控制方案进行仿真对比分析。考虑到控制器参数选择差异会对控制性能造成影响，首先进行定速定高飞行模式下的对比仿真试验(对比试验1)，目的在于寻找合适的控制器参数，使得本文方法与对比方法取得相近的控制效果，从而尽可能地避免控制器参数选择差异对控制性能带来的影响。仿真过程中飞行器速度设置为V=3429 m/s，飞行高度设置为H=20000 m，马赫数设置为M=10，大气密度设置为ρ=8.80×10-2kg/m3，发动机推力设置为T=1468000 N。飞行状态初始条件设置为α=0.83°,Q=0(°)/s,u=0°。攻角参考轨迹设置为：

(27)

控制器参数和初值设置如表3所示。

表3 控制器参数设置Table 3 Parameters settings of the controllers

图2 对比试验1中的攻角跟踪曲线Fig.2 Tracking curves of the angle of attack in comparative experiment 1

由图2、3可以看出，对于定速定高飞行模式，在表3所示控制器参数设置下，采用本文方法与对比方法均能得到较好的攻角跟踪控制效果。本文方法得到的跟踪误差更小，这是由于本文方法利用了气动系数的额定值，这是符合工程实际的。同时，可以看到采用本文方法时初始阶段攻角变化方向与参考轨迹的变化方向相反，这是由于指令滤波器的滤波信号在初始阶段存在偏差所致；同样可以看到在20 s附近攻角参考轨迹变小时，实际攻角并未向相反方向变化，这是因为此时指令滤波器滤波信号已收敛。

接下来，仍采用表3所示控制器参数设置，进行变速变高飞行模式下的仿真对比试验(对比试验2)。试验中飞行速度、高度和发动机推力变化设置为：

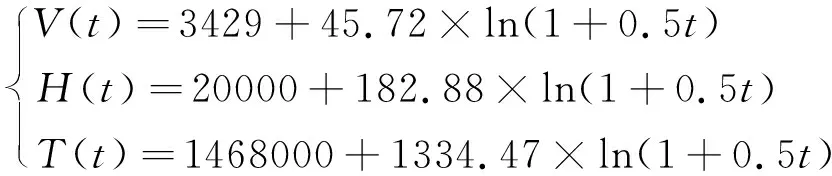
(28)

(29)

z0(0)=V(0),z2(0)=H(0),z1(0)=z3(0)=z4(0)=0然后基于式(4)可得ψ的计算公式为：

(30)

仿真过程中马赫数通过公式M(t)=V(t)/Vs计算，其中Vs表示声速。考虑到高度变化量较小，为简化数学模型的复杂度，声速取恒定值Vs=342.9 m/s，大气密度取恒定值ρ=8.80×10-2kg/m3。式(8)所示干扰观测器参数设置为l1=10,μ(α)=10α，干扰观测器初值设置为：

仿真过程中考虑模型参数不确定性的影响，设定式(2)中的气动参数存在-35%的偏差。仿真结果如图5～10所示：

图5和图6给出了两种方案下攻角的跟踪情况。可以看出，对比方法在变速变高飞行模式下控制效果较差，结合图4和图6可知，航迹倾角变化率越大时，对比方法的跟踪精度越差。而本文设计的方法取得了较好的控制效果，当攻角参考信号稳定时跟踪误差能够收敛至0附近。结合图3和图6可以看出本文算法的控制效果与航迹倾角及其变化率的大小无关。由对比试验1的结果可知两个方法取得的控制效果之间的差异并不是由于控制器参数设置造成的。以上结果表明本文方法能够适用于变速变高的飞行模式。

图3 对比试验1中的攻角跟踪误差Fig.3 Tracking errors of the angle of attack in comparative experiment 1

图4 对比试验2中航迹倾角及其导数的曲线Fig.4 Curves of the flight path angle and its derivative in comparative experiment 2

图5 对比试验2中的攻角跟踪曲线Fig.5 Tracking curves of the angle of attack in comparative experiment 2

图6 对比试验2中的攻角跟踪误差Fig.6 Tracking errors of the angle of attack in comparative experiment 2

图7给出了采用本文方法时式(8)所示干扰观测器对干扰量Δα的估计效果。可以看出，干扰观测器能够在较短时间内实现对干扰量的准确估计。

图7 对比试验2中的干扰量ΔαFig.7 Disturbance Δα in comparative experiment 2

图8 对比试验2中的俯仰角速度动态Fig.8 Dynamics of pitch rate in comparative experiment 2

图9给出了本文方法的俯仰角速度和控制量曲线。可以看出，俯仰角速度在飞行过程中保持稳定；控制量大小在表2规定的限制范围内。

图9 对比试验2中的俯仰角速度和升降襟副翼偏转角Fig.9 Pitch rate and deflections of elevons in comparative experiment 2

5 结 论

本文针对高超声速飞行器非仿射模型姿态控制问题提出了一种基于反步法的非线性控制方法。设计扩张状态观测器解决模型中的非仿射项，采用动态逆的方法设计了升降襟副翼的控制律。所提方法既能够适用于定速定高的飞行工况，又能够适用于变速变高的飞行工况。仿真结果表明，对于变速变高飞行模式，本文所设计方法在气动参数存在较大误差情况下仍能取得较高的控制精度；干扰观测器和扩张状态观测器能够较快地实现对干扰量和扩张状态进行有效估计。