考虑禁飞区规避的空天飞行器分段预测校正再入制导方法

章吉力,刘 凯,樊雅卓,佘智勇

(1.大连理工大学航空航天学院，大连 116024；2.北京空天技术研究所，北京 100074)

0 引 言

随着高超声速技术的发展，可重复使用空天飞行器为空间往返提供了新的方案。与传统运载方式相比，空天飞行器具有廉价、快速、可靠、便捷等优势[1-3]，具有重要的军事和民用价值。

对于采用升力式构型的空天飞行器，其再入制导问题[4-9]是实现自由出入空间的关键难点之一。空天飞行器再入返回过程中，不仅需要考虑力热载荷要求带来的动压、过载和热流等约束，还应充分考虑返场需求对应的终端速度、高度及航程约束，同时覆盖姿态控制幅值和响应速度约束的要求；此外，空天飞行器离轨过程中飞行速度大，施加脉冲制动存在的微小误差将被放大，进而导致再入初始状态偏差较大，表现为再入点初始位置和能量散布大；再入过程中历经真空、临近空间及稠密大气层，复杂气动环境带来较大不确定性。综合来看，在初始散布误差和模型不确定性较大的情况下，狭窄飞行走廊中实现高精度再入制导面临挑战。

为了解决再入制导问题，文献[10]提出了基于阻力加速度设计再入轨迹的方法，这种方法在航天飞机上得到了应用。也有学者尝试使用推导解析解的方式设计指导律，在此基础上发展出解析预测制导，这类方法[11-12]往往依赖于一些特定的假设，在早期飞行器搭载计算机计算能力不足的情况下也进行了一些应用。随着计算机技术的发展和计算能力的提升，基于数值积分的预测—校正方法成为了国内外学者研究的重点。数值预测—校正算法通过对动力学方程进行积分来预测终端状态，文献[13]详细介绍了一种横向制导策略，定义待飞航程为当前位置到航向校准圆柱的地表距离，通过待飞航程和航向角定义了横程。文献[14]应用了这种横向制导策略，同时提出了一种纵向制导策略，定义终端到航向校准圆柱的地表距离为剩余航程，通过数值积分预测终端经纬度，进而得到剩余航程，进行倾侧角迭代。文献[15]以低升力结构的飞行器为背景应用了预测—校正制导，并取得了很高的精度。

还有许多学者针对更加具体的任务形式对预测—校正制导做出了一些改进。文献[16]在火星大气进入的背景下考虑到倾侧角多次反号会产生燃料消耗过多的问题，把预测环节引入了侧向制导中，给出了只经过一次反转就使末端横程为零的侧向制导律。文献[17]应用准平衡滑翔条件(QEGC)来进行攻角设计，进而得到再入轨迹。考虑到对于高升阻比RLV的QEGC约束过于苛刻，文献[18]将地球自转的哥氏加速度引入QEGC，得到改进的准平衡滑翔条件，在合理的前提下放宽了倾侧角幅值约束。

针对禁飞区规避问题，文献[19]和文献[20]在过程约束中添加了禁飞区的约束，当飞行器靠近禁飞区时，采用一种独立的更高优先级的侧向制导逻辑，通过变更飞行器的航向来规避禁飞区。文献[21]通过建立精确再入模型，采用SNOPT求解避开禁飞区的轨迹，并进行跟踪。文献[22]根据再入不同时刻的特点在指令点处通过预测生成触角，验证了规避多种不同形状的禁飞区的可行性。

文中提出一种基于分段目标函数的预测校正再入制导方法，在再入段前期仍然采用剩余航程作为指标进行倾侧角指令迭代计算，在再入段后期引入预测落点偏差作为目标函数进行制导指令求解，兼顾了计算效率与终端制导精度。在此基础上，针对规避禁飞区采用幅值修正策略实现侧向制导，可适用于无法单独通过倾侧角反号策略规避禁飞区的情况。

1 空天飞行器再入问题建模

1.1 再入问题的动力学方程

空天飞行器再入动力学模型在弹道坐标系中建立，采用倾斜转弯模式(Bank to turn, BTT),整个再入过程均为无动力状态，在考虑球形大地和地球自转的基础上，式(1)给出三维质点动力学模型：

(1)

式中：V是速度，γ是弹道倾角，ψ是弹道偏角，r是地心距，表示飞行器到地心的距离，λ是飞行器在地表投影点的经度，φ是飞行器在地表投影点的纬度；g是重力加速度,其中g0=9.8067 m/s2，m是飞行器的质量，ωe是地球自转的角速度。σ是倾侧角，D是阻力，L是升力，L和D的计算方法由式(2)给出：

(2)

式中：ρ表示大气密度，可以视为高度的函数，A为参考面积，CL和CD分别表示升力和阻力系数，可以视为是攻角和马赫数的函数。再入过程的控制变量一般只有攻角α和倾侧角σ，在设计再入弹道的过程中，攻角α的值由事先设定好的α-V剖面给出。预测校正制导算法能够通过给定的倾侧角对动力学模型进行积分，进而预测剩余航程和落点，并基于此进行迭代，得到满足航程要求的倾侧角。

1.2 再入问题的过程约束和终端约束

典型的再入过程约束由下式给出：

(3)

(4)

(5)

典型的再入过程终端约束包括，终端的高度，速度以及剩余航程约束。高度和速度又可以用归一化的能量e来进行统一表示：

(6)

所以终端状态约束可以表示为：

(7)

式中:ef表示终端能量，S是剩余航程，Sf是剩余航程的边界值。

2 分段预测校正制导算法

预测—校正制导方法是以消除实际飞行轨迹的预测落点和期望落点之间的偏差为目的的制导方法。这里重点讨论数值预测校正制导方法，对现有预测算法的目标函数提出分段策略，具体来说，在速度大于某一阈值时，使用剩余航程作为目标函数进行迭代，当速度低于该阈值后，改用落点偏差作为目标函数进行迭代，基于落点偏差的目标函数在再入后期兼具纵向和横侧向制导功能，不需要额外设计横侧向制导逻辑。对再入制导过程中的禁飞区约束，首先通过计算飞行器同禁飞区中心的距离来判断飞行器是否需要适用禁飞区规避逻辑，若飞行器与禁飞区的距离达到阈值，则通过更高优先级的禁飞区制导逻辑给出规避策略，覆盖原有制导指令。算法整体逻辑由图1给出。

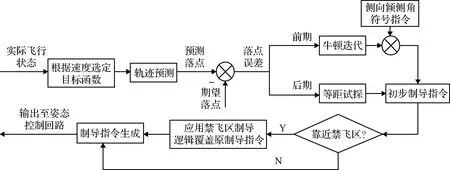
图1 分段预测校正制导算法流程Fig.1 Piecewise predictor-corrector algorithm

2.1 约束转化与再入走廊

在再入过程中，飞行器始终要遵守约束条件。但是，在全程计算和判断所有的约束是否都能满足是难以实现的，这会极大地加大运算量。事实上，由于各个约束中均含有倾侧角，可以把飞行过程中的热流约束、动压约束和过载约束全都转化为倾侧角的约束。

如图2所示，在H—V剖面上,高度的下界由动压、过载、热流约束的最大值决定，即：

图2 过程约束下的再入走廊Fig.2 Reentry corridor under constraints

Hmin=max(Hq,Hn,HQ)

(8)

若已知r和V，就可以求出对应的σ值。根据已经得到的Hmin，可以求得对应的地心距rmin，对应的倾侧角边界由下式给出：

|σ|max(V)=|σ|(rmin(V),V)

(9)

所以，控制指令σ需要满足：

|σ(V)|=

(10)

式中:σi是由预测环节的迭代算法给出的倾侧角幅值，|σ|决定了飞行器在再入过程中的改变航向能力。

2.2 纵向制导逻辑

如前文所述，数值预测校正制导算法的最终目的是生成倾侧角指令,而纵向制导部分的任务是确定倾侧角的幅值。

2.2.1航程预测环节

现有的预测校正制导方法大多使用积分方式获取预测环节的剩余航程，并以此来迭代制导指令。然而，在再入过程接近终端时，首先剩余航程的值很小，这很可能会造成目标函数没有零解，迭代发散，使算法无法获得正确的倾侧角指令；其次，预测环节是需要在反复迭代中进行的环节，是算法计算量的最主要部分，对剩余航程的导数进行积分来计算剩余航程的过程会带来巨大的计算量；最后，面对有禁飞区规避需求的再入问题，飞行器实际飞行的航程会远大于预设标称轨迹的航程，通过积分计算得到的预测航程实质上不再具备校正能力。为了解决这些问题，采用基于预测落点计算航程的方法来代替积分计算剩余航程。提出了一种不进行积分计算航程新方法。

通过对动力学模型式的积分，可以得到空天飞行器在每个时刻的位置和速度信息。再入航程定义在飞行过程的纵平面内。Ω是与再入航程相对应的地心角。因此，通过给定一个初始的倾侧角，算法的预测环节就可以预测飞行器的最终落点的经纬度，该倾侧角对应的再入航程可以用式(11)来计算:

(11)

2.2.2基于分段目标函数的指令校正环节

指令校正环节通过迭代来实现倾侧角值的求解，现有的校正方法大多使用基于积分剩余航程的单一目标函数来进行求零迭代，前面已经提到，对于有禁飞区规避需求的再入问题，该目标函数已经不具备好的校正能力；另一方面，在接近终端时，纵向制导与横侧向制导的耦合影响将会更加显著，大幅值倾侧角的存在和航向走廊的收紧会产生频繁的航向切换，导致控制指令的震荡和制导精度的下降。为了获取相对稳定的控制指令，提升再入制导的精度，这里提出分段目标函数的方法，取迭代的目标函数为：

(12)

与传统目标函数相比，式(12)引入预测落点同目标落点的距离作为后期目标函数，这一距离实质上也就是落点误差的表征。

式中:Vs是切换目标函数时的速度，Sp是预测得到的当前点的剩余航程，其计算方法已由式(11)给出。S是当前点到目标点的实际地面航程，S的计算方法为：

(13)

式中:λ，φ是当前点的经纬度，λf，φf是目标点的经纬度，Ω是S对应的地心角。

(14)

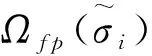
在航程预测环节获得了在给定倾侧角下的航程之后，对于V>Vs的情况，通过牛顿迭代来求解符合要求的倾侧角指令，如式(15)所示：

(15)

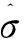
分段目标函数最大的优势在于，Sfp是落点误差的直接表征，以Sfp为目标函数进行迭代能够显著减小落点误差。

2.3 侧向制导逻辑

在现有的研究中，侧向制导就是要通过合理的定义倾侧角反转逻辑来实现，反转逻辑的设计一般通过定义横程和横程边界来实现，横程有多种定义方法，对于不同定义的横程，就要设计不同的横程边界。横程边界多被设计为漏斗形，由于漏斗嘴部边界收紧，会造成临近终端的侧倾反转过于频繁，若设置比较宽泛的横程边界，则落点精度约束难以满足。而分段目标函数的引入，可以直接通过设置制导指令的更新时间来控制倾侧角的反转次数，避免了终端边界设计的困难。

在V>Vs时，定义横程表示沿当前状态飞行至终端后的落点误差大小，其的定义如下：

Z=arcsin(sinΩsinΔψ)

(16)

式中：Ω由式(13)定义给出，Δψ=ψs-ψ是航向偏差，为速度和待飞位移的夹角，这种定义方法在倾侧角变号时，横程可以很快响应，有较好的控制效果，由于航向偏差是以目标落点为基准，这可以保证轨迹会逐渐趋向于目标落点。

横程的上下边界设计为：

(17)

式中:k1，k2为可调参数。至此，倾侧角符号翻转逻辑为：

(18)

因此当前使用倾侧角指令变为

(19)

在V≤Vs时，由于纵向制导采用等距试探法，其自身实质上兼具了求解倾侧角幅值和符号的能力，不需要额外设计侧向制导策略，也就无需为反转设计边界。

2.4 禁飞区规避制导逻辑

考虑将禁飞区分为两个大类，第I类禁飞区是可以通过倾侧角反号规避的禁飞区，第II类禁飞区是不可以通过倾侧角反号规避的禁飞区，并以圆柱形禁飞区为例讨论这两种禁飞区的规避策略。

当飞行器靠近禁飞区时，开始弃用原有侧向控制逻辑转入禁飞区规避侧向控制逻辑，确认飞离禁飞区周边到达安全区域后，重新转为使用原有侧向控制逻辑。针对规避问题，启用禁飞区规避侧向控制逻辑的条件由式(20)给出：

Sn≤n0Rn，λ≤λn

(20)

式中:Sn是飞行器到禁飞区中心的地表距离，Rn是禁飞区的半径，λn是禁飞区中心的经度,n0是一设定常数。

首先求解飞行器到禁飞区中心的距离Sn，求解方法与航程求解方法相似：

(21)

式中：λn，φn是禁飞区中心的经纬度，Ωn是Sn对应的地心角。

定义对禁飞区的中心视线角为：

ψn=arcsin[sin(λn-λ)cosφ/sinΔn]

(22)

为了确定从禁飞区的上方还是下方来进行规避，要将ψn同当前弹道偏角作比较，若ψ≤ψn，则从禁飞区上方规避；若ψ>ψn，则从禁飞区下方规避，之后，求解自禁飞区上方飞过能够使用的最大视线角ψmax和自禁飞区下方飞过能够使用的最小视线角ψmin：

(23)

图3是禁飞区相关的角度示意图，值得注意的是，当取正北方向为参考时，各视线角的幅值满足|ψmax|<|ψn|<|ψmin|。

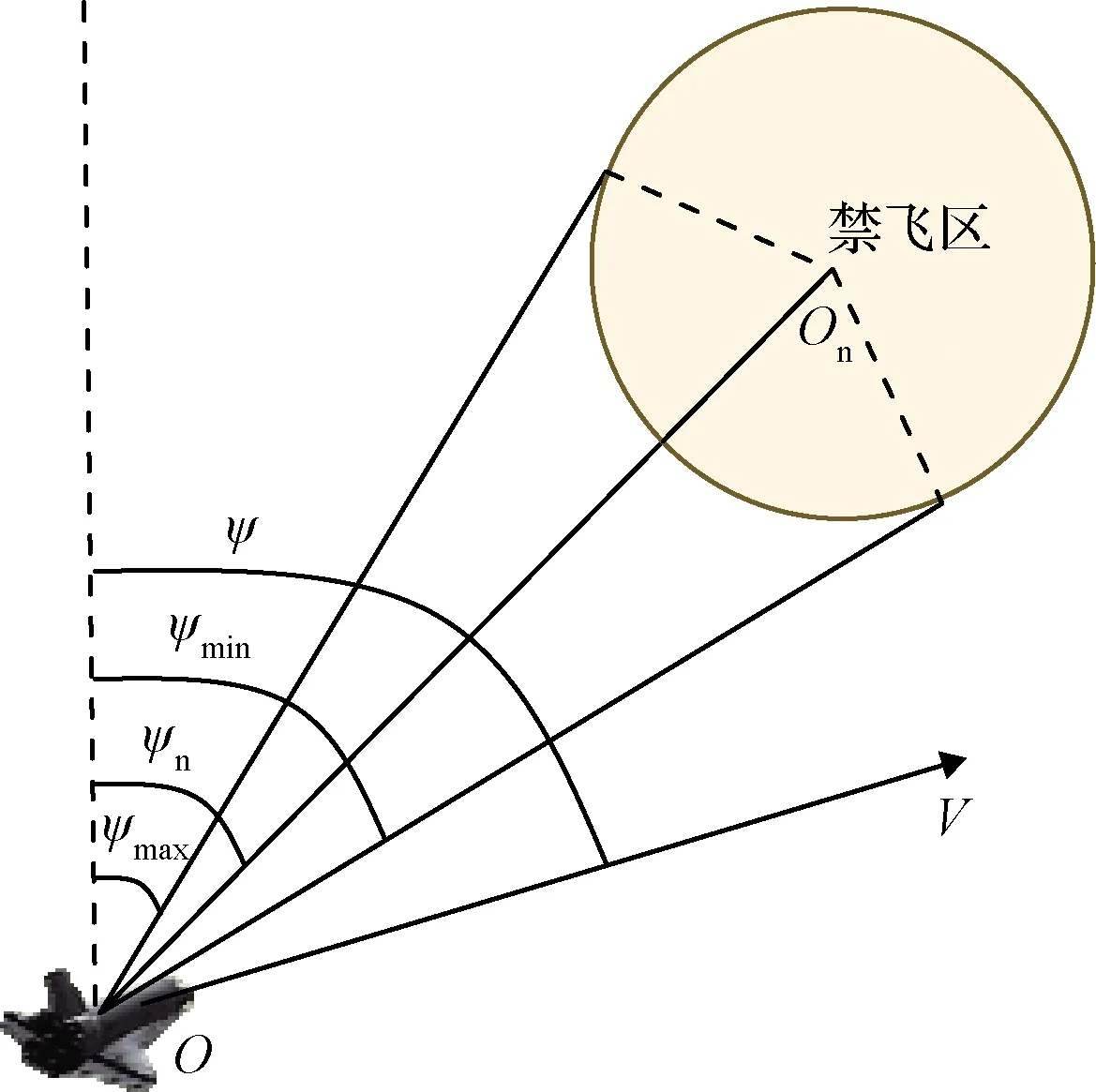
图3 禁飞区相关角度示意图Fig.3 Angles about the no-fly zone

图4为某空天飞行器再入轨迹地面投影图，倾侧角的符号能够改变地面轨迹的凹凸性。A和B是两个圆柱形禁飞区，轨迹1是不采取禁飞区规避逻辑得到的轨迹，容易发现，轨迹1穿过了禁飞区A，通过倾侧角反号使轨迹向上偏离即可实现对禁飞区A的规避，故禁飞区A属于可以通过倾侧角反号规避的禁飞区，也就是第I类禁飞区。应用规避算法绕开禁飞区A后，飞行器沿着轨迹2飞行，会穿过禁飞区B，此时即便倾侧角反号使轨迹向上偏离，飞行器仍然会穿过禁飞区B，因此故禁飞区B属于不可以通过倾侧角反号规避的禁飞区，也就是第II类禁飞区。

图4 某空天飞行器再入轨迹地面投影Fig.4 Subsatellite track of the reentry trajectory of an aerospace vehicle

对于第I类禁飞区，采用倾侧角反转逻辑规避，当式(20)和规避条件同时满足时，倾侧角反号。禁飞区的规避条件由式(24)给出：

(24)

对于第II类禁飞区，采用倾侧角幅值增大来规避，当式(20)和式(24)同时满足时，增大倾侧角的幅值：

(25)

式中：σn为一大于零的定值。

3 仿真分析与制导性能评估

以空天飞行器的再入阶段为例进行仿真分析，仿真对象为某具有升力结构的空天飞行器，再入点的初始状态如表1所示：

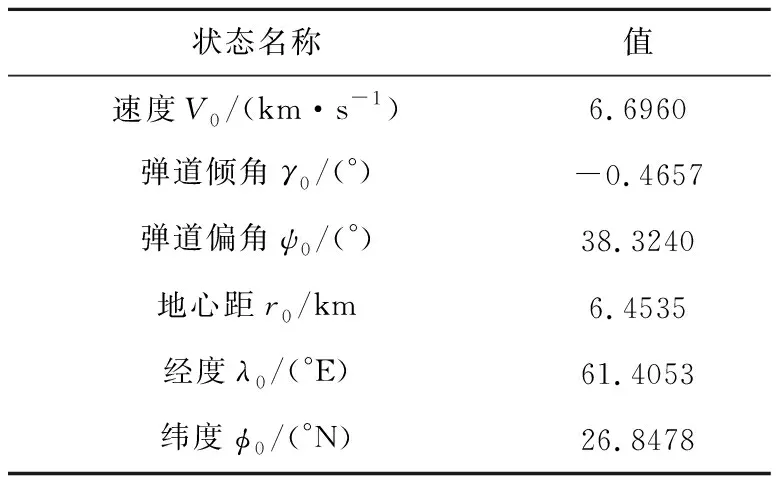
表1 再入点初始条件Table 1 The initial conditions of the re-entry point

表2给出了目标落点的相关信息：

表2 目标落点相关信息Table 2 The conditions of the drop point

表3给出了再入问题的过程约束值：

表3 再入过程约束Table 3 Constraints of the re-entry process

考虑到空天飞行器为面对称结构，各个方向的过载及承受过载的大小和能力均有所区别，因此过载约束沿体轴系三个方向分解后给出，三向过载需同时满足约束。

3.1 标称制导仿真

利用提出的分段预测校正制导方法，在给定的名义初始条件下进入再入制导仿真，仿真结果如图5所示。

如图5-图7所示：制导算法能够满足速度、高度等终端约束。从图8可以看出，倾侧角在A、B两点分别作出反转和增大幅值的指令，以此来规避禁飞区A和禁飞区B，临近终端时，由于侧向机动仍然存在，为了对准目标，需要进行多次倾侧角的反转，为了避免倾侧角反转过于频繁，设置制导更新间隔为10 s，这就保证了倾侧角符号反转的频次间隔在10 s以上。此外，从图10中可以发现，不加入规避策略的仿真飞行轨迹将穿越禁飞区。标称情况下，再入制导落点误差为809 m。各项过程指标也在约束范围之内。

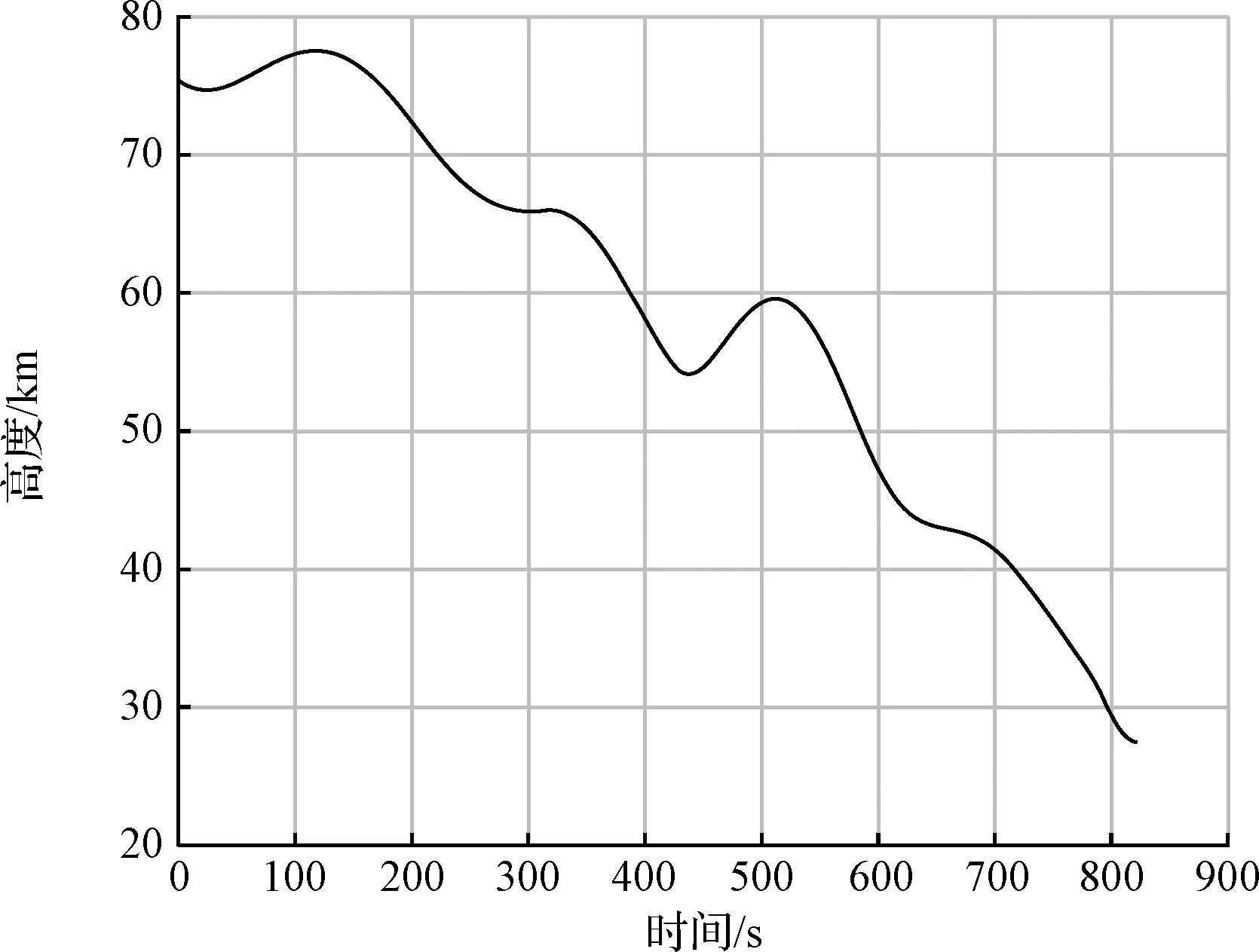
图5 高度—时间Fig.5 Altitude-time

图6 速度—时间Fig.6 Velocity-time

图7 归一化能量—时间Fig.7 Normalized Energy-time

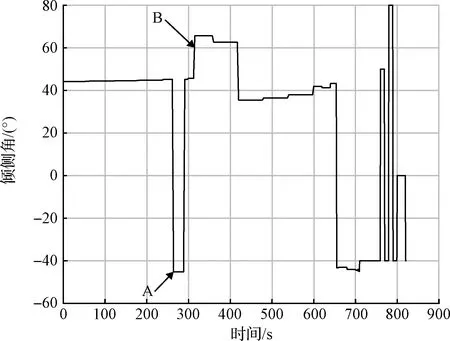
图8 倾侧角—时间Fig.8 Bank angle-time

图9 过程约束—时间Fig.9 Process constraints -time

图10 地面轨迹—时间Fig.10 Subsatellite track-time

3.2 单段/分段预测校正制导的蒙特卡罗对比仿真

蒙特卡罗仿真是检验算法鲁棒性的重要工作，本节将分别对目标函数未分段和目标函数分段的预测校正制导算法进行蒙特卡罗仿真验证，比较二者的制导精度。每种方法的仿真次数为20次。

影响轨迹的参数主要涉及能量、气动品质、再入点初始位置误差。综合考虑这些影响，蒙特卡罗仿真的不确定性参数由表4所示：

表4 蒙特卡罗仿真不确定性参数Table 4 The uncertain parameter of Monte Carlo simulation

在表4不确定性参数影响下，两种制导方法各20次仿真的落点位置散布如图11所示。

图11 落点误差对比Fig.11 Drop point error contrast

可以看到，采用单段目标函数的落点精度不够理想，绝大部分点落点误差在10 km内。使用分段目标函数之后，绝大多数落点误差在2.5 km内，所有落点均在5 km误差边界以内，落点精度较单段目标函数的预测校正制导策略有显著提升。

4 结 论

作为对现有数值预测校正再入制导方法的改进，通过在再入过程后期引入新的目标函数来提升制导的精度，该目标函数能够直接表征落点误差，在提升计算速度和稳定性的基础上兼具纵向和横侧向制导的功能，可以直接给出包含符号的最优倾侧角指令。在禁飞区规避策略方面，通过把禁飞区分为两个大类，分别提出了适用的规避策略。算法的蒙特卡罗仿真结果表明，分段目标函数的预测校正算法在空天飞行器再入阶段应用性能良好，落点精度更高，同时能够有效实现对禁飞区的规避飞行。