一种基于飞行任务的临近空间短距滑翔飞行器弹道预示方法

2021-02-23王开园万佳庆

宇航学报 2021年1期

王开园，许志，唐硕，万佳庆,3

(1. 西北工业大学航天学院，西安 710072；2. 陕西省空天飞行器设计重点实验室，西安 710072；3. 江南机电设计研究所，贵阳 550009)

0 引言

高超声速滑翔飞行器[1-2](Hypersonic glide vehicle, HGV)，具有大空域、高机动、弹道模式多变等飞行特点，导致反导武器在速度和过载不占绝对优势的条件下，拦截该类飞行器时，需要通过预测目标轨迹[3-4]的方式来提高拦截精度。轨迹预测一般通过对目标当前状态的连续跟踪、辨识实现其未来一段时间内飞行轨迹预测，其实质是基于机动特征参数的状态量时间序列预测问题。

现有的轨迹预测方法[5-8]主要集中在基于动力学模型的相关方法研究，通过轨迹跟踪研究气动参数、升阻比或控制参数的变化规律，结合机动模型实现轨迹预测。这种未考虑飞行终端状态约束的机动模式，随着预示时间增加会导致预测误差逐步增大，因此有效预测时间窗口十分有限。文献[8]通过估计气动相关参数构建覆盖目标典型机动模式的模型集，并结合飞行意图判断机动模式，这种通过气动参量覆盖目标典型机动模式的方法物理意义不明显，且主要考虑航迹约束，不能体现飞行任务条件下的能量约束。

由于临近空间滑翔飞行器机动方式复杂，并不能够由单一的运动模型来统一表述，因此包含多个机动模型的交互式多模型滤波(Interacting multiple model, IMM)在这类目标的跟踪中广泛应用[9-10]。但是，机动模式多变情况下，轨迹跟踪方法的稳定性面临问题。文献[11]通过构建自适应网格IMM,在不增加模型集规模的情况下，提升了模型集对目标机动模式的覆盖能力；标准IMM中Markov概率转移矩阵是根据先验信息确定，不符合短距滑翔飞行器机动模式多变的特性，需要对Markov概率转移矩阵进行修正[12]。强跟踪滤波器通过渐消因子使得残差序列在每一步相互正交，具有很好的模型参数失配的鲁棒性[13-14]。

虽然，文献[5-7]对中远程机动滑翔目标如HTV-2，AHW等，采用气动特征参数拟合的轨迹预测方法具有一定的适应性，但是对于动力学模型强时变、高度非线性，控制量模型多变的短距滑翔飞行器会出现较大的预测误差。因此，本文基于飞行任务的先验信息，在典型机动模式下结合自适应网格，构建了适应性强且物理意义明确的目标机动模型；针对机动模型不匹配引起的滤波发散问题，通过引入渐消因子、修正Markov概率转移矩阵对IMM算法进行改进，提升滤波方法对短距滑翔飞行器轨迹跟踪问题的适应性。

1 问题描述

1.1 动力学模型

高超声速飞行器飞行过程中，为便于研究高度、速度、航迹角、气动力加速度等变量之间的关系，在半速度坐标系[15]下进行机动模型建模。假设地球为非旋转圆球模型，相应半速度坐标系下的动力学方程为：

(1)

式中：地心距R、经度θ、纬度φ为表征飞行器位置信息的状态量，速度V、航迹角γ、航向角ψ为表征速度信息的状态量，D和L分别代表阻力加速度大小、升力加速度的大小，σ代表倾侧角指令。

在进行轨迹跟踪、预测仿真时，需要建立雷达测量坐标系模拟雷达测量信息。雷达测量坐标系orxryrzr以雷达站or为坐标原点采用北天东坐标系，其中oexeyeze为地心系，φT,φD分别为雷达站的经度、纬度，如图1所示。

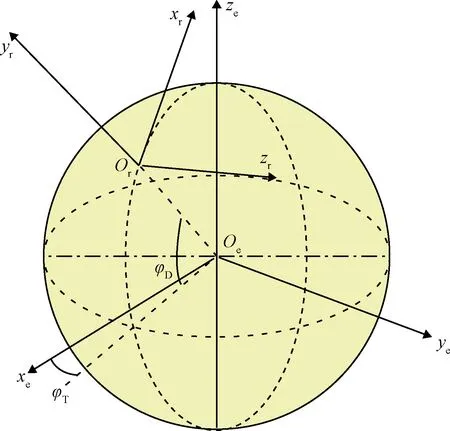
图1 雷达参考坐标系Fig.1 Radar reference frame

图2 雷达测量示意图Fig.2 Radar measurement diagram

(2)

动力学方程构建是机动模型建模的基础，而雷达测量坐标系的建立是进行雷达伪观测量以及滤波方程构建的基础。

1.2 短距滑翔弹道预示问题

为扩大拦截区域[17]，降低拦截弹需用过载，改善制导律，进而降低目标机动对脱靶量的影响，通常反临近空间滑翔飞行器的拦截中制导以预测命中点为终端约束，因此需对目标飞行器进行弹道预示提供反临先验知识[3-4]。弹道预示需要基于先验信息，在飞行意图约束下，以雷达观测量为输入，以当前轨迹跟踪结果为起始点进行时间序列预测，最终轨迹预测形式是一个随跟踪预测进程不断动态更新的时间序列，如式(3)所示：

(3)

式中：X(t)代表滑翔飞行器的位置、速度信息，u(t)表示更新的加速度控制参量，Y(t)为拦截弹所需交班条件包含位置、交会角等信息。

不同于HTV-2、AHW等中远程滑翔飞行器，临近空间短距滑翔飞行器主要特点是：在滑翔段要覆盖机动射程200 km～400 km范围，且横程具有200 km机动能力；为保障中末制导交班条件以实现最大程度毁伤，该阶段速度要从Ma10减速到Ma3，以致其必须进行大范围减速机动才能实现任务要求，高度-速度飞行剖面如图3所示。同时短距滑翔飞行器滑翔段飞行时间较短，不能像中远距滑翔飞行器在线通过对滑翔段轨迹的观测提取飞行器气动特征参数等，因此传统的基于轨迹成型的弹道预示方法已不再适用。

图3 飞行剖面及走廊示意图Fig.3 Sketch of flight profile and corridor

为保障末制导毁伤效果，中末制导交班条件如式(4)所描述，Hf，Vf，Sf分别为末端高度、速度、剩余航程，Hs，Vs，Ss为末段制导阶段需求的高度、速度、航程，ΔH，ΔV，ΔS描述了相应交班窗口的大小。

(4)

高超声速飞行器的轨迹跟踪结果反映了目标当前的飞行状态，待攻击的目标点及滑翔段-末制导交班条件则反映了短距滑翔飞行器滑翔段的飞行意图。如图4所示，由于短距滑翔飞行器具有机动模式多变、弹道参数变化剧烈，仅依靠当前飞行状态拟合机动参数进行轨迹预测会因弹道参数变化剧烈出现较大偏差[5-7]，而仅依靠飞行意图进行轨迹预测会出现飞行过程中轨迹预测偏差较大的情况。本文所提出的基于飞行任务的轨迹预测方法通过结合飞行状态以及飞行意图两部分信息，提升轨迹跟踪以及预测的精度。

图4 不同轨迹预测方案示意图Fig.4 Schematic of different trajectory prediction schemes

因此，对高超声速短距滑翔飞行器进行高精度轨迹预示，必须同时考虑目标当前飞行状态以及飞行目的。即首先在飞行意图等先验信息下，构建基于飞行任务的机动模型集，实现对目标轨迹的高精度、稳定跟踪以及机动特征参数的求解；其次基于机动特征参数，结合动力学模型以及飞行意图求解控制参量，进行轨迹时间序列预测。

2 基于飞行任务的变结构IMM轨迹跟踪

基于动力学模型，结合飞行任务构建目标机动模型，通过改进的IMM进行轨迹跟踪，并辨识机动特征参数，需要进一步解决以下问题[9-13]：

1)构建能覆盖目标典型机动模式的模型集。

2)构建对模型偏差具有较强适应能力的滤波方法，由于覆盖目标典型机动模式本身意味着存在模型偏差大的情况，因此需提升滤波算法的稳定性。

3)提升IMM算法模型集的在线自适应能力，即在线的模型参数调整和模型的快速切换。

2.1 模型集设计

临近空间滑翔飞行器的飞行任务是在热流、动压、过载、准平衡滑翔等过程约束下，解决将目标从当前状态送至终端目标点的两点边值问题。为进行轨迹跟踪和预测的机动模型建模，在模型集设计时需要将飞行任务中的状态量和飞行意图等信息通过飞行任务剖面转化为加速度。转化过程所涉及到的飞行任务剖面包含：阻力加速度-速度剖面(D-V)、高度-速度剖面[18](H-V)以及侧向飞行边界[19-20]。

高超声速飞行器在滑翔段航迹角较小的情况下近似用V/D相对于V的积分描述剩余航程：

(5)

反之，在D-V剖面形式固定时，根据剩余航程实时确定阻力加速度。同时，通过先验分析知，H-V剖面基本呈线性变化，可近似用多项式(6)表述：

H=anVn+…+a1V+a0

(6)

在当前飞行状态、中末制导交班条件以及飞行过程约束的基础上，对部分参数进行离散设计，构建可覆盖不同机动模式的H-V剖面。通过D-V剖面，H-V剖面推导γ′(V)的函数形式，并结合动力学模型中的dγ/dV，确定D-V剖面，H-V剖面和纵向升力加速度LY的内在联系。由弹道系下的运动学方程(1)可得：

(7)

其中，D为阻力加速度的大小，相应求解可得航迹角和速度的关系γ=f(V)：

(8)

式(8)中航迹角γ对速度V求导，即求解γ′(V)：

(9)

另由式(1)可知：

(10)

式(9)、式(10)联立可得纵向升力加速度：

LY=-γ′(V)·V(D+gsinγ)-(V2/R-g)cosγ

(11)

高超声速飞行器在滑翔段升阻比NL/D变化规律相对统一，针对NL/D进行离散设计，求解侧向升力加速度大小：

(12)

由于短距滑翔飞行器飞行意图明确，本文通过飞行轨迹侧向边界确定倾侧角符号，将侧向飞行视线角误差δZ限制在一定范围内，一般通过航向角和视线角偏差表示：

δZ=ψ-arctan((ZT-Z)/(XT-X))

(13)

其中，ψ为航向角,ZT，XT为北天东坐标系下目标点位置量，Z，X为北天东坐标系下飞行器当前位置量。对于侧向边界模型的设计，采用一种随速度单调减小的形式：

|δc|=δ0(V-VS)/V

(14)

式中：δ0为滑翔过程中的视线角约束，假设可由先验信息获知。通过离散设计参量VS构建侧向边界模型集，最终得到加速度指令控制参量u(t)，具体模型集构建原理如图5所示。

图5 模型集构建原理Fig.5 Model set construction principle

2.2 引入渐消因子的容积卡尔曼滤波

机动模型集覆盖了可能的典型机动模式，即存在和目标真实运动模型偏差较大的情况，为防止滤波过程发散，需提升滤波方法的稳定性。基于数值积分规则的容积卡尔曼滤波器[21]相较无迹卡尔曼滤波、高斯卡尔曼滤波、中心差分卡尔曼滤波等有更好的非线性逼近性能、数值精度以及稳定性。强跟踪滤波[22]算法(Strong tracking filter, STF)是建立在输出残差序列正交性原理上的卡尔曼滤波器，通过对状态预测协方差阵引入渐消因子，在线实时调整增益矩阵，强迫输出的残差序列正交，可有效解决由模型不准确带来的鲁棒性差、滤波发散等问题。渐消因子计算过程如式(15)所示。

(15)

通过渐消因子对协方差阵进行修正，得到更新的一步预测状态协方差阵：

(16)

2.3 基于ACKF的交互式多模型滤波

由于预先不能很好地确定目标的机动模式，因此次单一运动模型无法准确描述目标的飞行状态。交互式多模型算法利用多个运动模型的相互组合，通过有效的加权融合进行系统状态估计。IMM同ACKF结合[23]的具体原理如图6所示。

图6 变结构IMM轨迹跟踪示意图Fig.6 Schematic diagram of variable structure IMM trajectory tracking

图6中不同于IMM-CKF的部分在各机动模型的概率估计工作。对IMM-ACKF中的概率估计过程进行说明，各模型的似然函数值为：

(17)

式(17)中：

(18)

(19)

2.4 自适应网格及概率转移矩阵设计

1)自适应网格的设计

模型集中心参数的调整以模型后验概率为权系数得出：

The maximal destructive interference positions on the intensity distribution I(r1) predict the ring radii of the GO lens with a focal length f. In the meantime, the diameter is decided by the number of rings. In this way, the lenses can be designed according to different incident fields ().

(20)

系统模型不准确、观测误差的影响、模型间的相互竞争等，会造成模型的后验概率的最大值并不是总出现在与真实模型最接近的模型处，因此容易导致中心模型围绕真实模型空间不断跃变、抖动甚至发散。对网格中心调整进行改进：

(2)为防止网格中心的过度剧烈变化，同时减小网格中心在移动时的距离总长，引入平滑因子[28]α：

(21)

对于网格间距的调整，按如下规则：

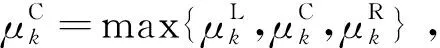
(22)

其中，t1为后验概率门限值，若左右两侧模型的后验概率小于t1，则该模型参量与当前机动模式不匹配，缩小与网格中心的间隔。

(23)

(24)

2)模型转移概率自适应设计

(25)

采用如下方法对Markov概率转移矩阵的元素进行修正：

(26)

(27)

其中，ξ用于控制调节的快慢。相应的概率转移矩阵转变为

(28)

(29)

3 轨迹预测

轨迹跟踪可以获取目标飞行器当前信息包含状态信息、各机动模型参数以及概率分布，而进行轨迹预测的关键是基于当前信息对控制参量的求解。

假设目标飞行器来袭时，能通过天基高轨卫星进行预警，天基中低轨卫星进行下视探测，根据光电特性、弹道特性等初步判断目标飞行器类型。通过前期情报搜集、弹道反设计等对弹道特性相关参数进行统计分析。

轨迹预测问题的实质是基于机动特征参数的状态量时间序列预测问题。即以先验提取特征信息为基础，以雷达观测信息为输入，通过轨迹跟踪辨识表征目标机动模式的特征参数，不断更新动力学模型下的控制参数，进而通过数值积分实现轨迹时序预测。具体预测流程如图7所示。

图7 轨迹预测流程图Fig.7 Trajectory prediction flowchart

图7中的离线工作为先验信息的获取部分，通过预先的情报搜集、弹道反设计等进行相关参量的统计、提取，假设这部分工作已经预先完成。在线部分，首先根据天基卫星、地基雷达等进行目标类型识别，并结合飞行器可达域初步判定可能攻击的目标；然后通过模型集设计、变结构IMM等实现控制参数辨识；通过更新加速度指令[29]控制参数u(t)，结合飞行动力学模型进行数值积分(见式(3))，实现轨迹的时序预测。由于同时存在多个机动模型，最终给出的轨迹预测形式是有一定概率分布的预测轨迹簇。

4 仿真校验

4.1 仿真条件设计

为了校验所提出的基于飞行任务的轨迹跟踪、预示算法的有效性，本文以一种短距滑翔飞行器为研究对象，设计了多约束条件下的滑翔段典型机动轨迹，如图8所示。

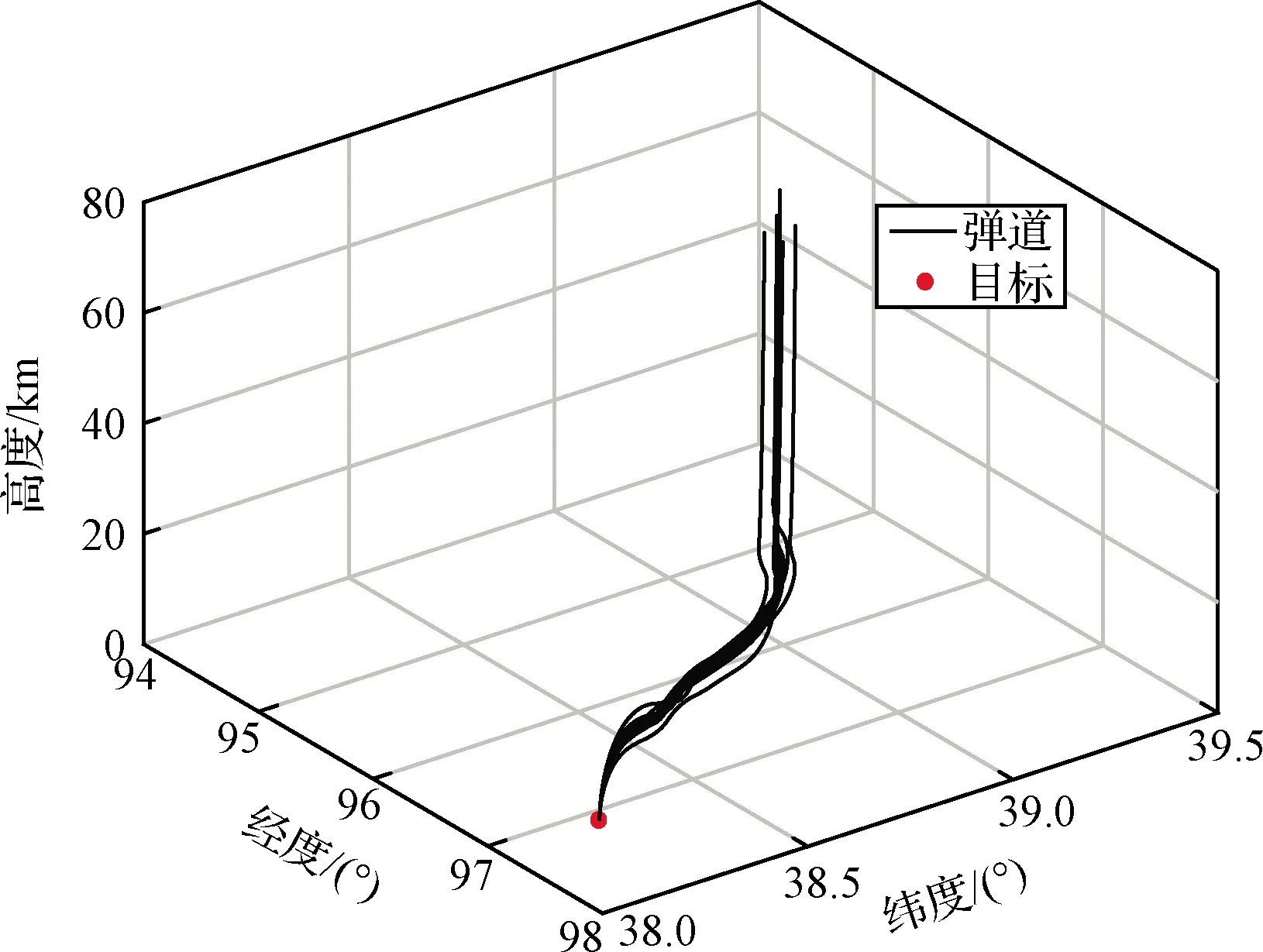
图8 典型制导方案下的轨迹仿真Fig.8 Trajectory simulation under typical guidance scheme

目标跟踪研究中的滤波器仿真周期主要受雷达数据更新率的限制，进入稳定跟踪后，相控阵雷达的数据输出率可达0.1秒每次，本文仿真认为雷达已经进入了稳定跟踪状态，状态参数更新周期取为0.1 s。相关测量精度如表1所示。

表1 雷达测量相关参数Table 1 Comparison of accuracy between two tracking methods

在进行模型集设计时，通过对该类短距滑翔飞行器典型制导方案下的多条轨迹进行分析，将模型集相关参数进行如下设计：

1)阻力加速度在全段近似为常值，因此将D-V剖面作为常值设计，在线根据剩余航程解算。

2)H-V剖面可近似用二次多项式表述H=a2V2+a1V+a0，通过离散设计二次项系数，结合实时状态和中末制导交班条件确定该剖面。

3)根据先验统计，NL/D在滑翔段近似为常值，因此使用统计得到的结果离散设计。

4)表征侧向边界的参量VS根据统计结果并结合先验信息进行离散设计。通过离散设计H-V剖面二次项系数a2，NL/D，VS构建出27个机动模型，各机动模型初始似然概率均为1/27。将模型集参数同所设计轨迹跟踪算法相结合，通过参数调节，Markov模型转移概率自适应过程中的用于控制调节快慢的参数ξ设置为0.95，主对角线元素阈值Th设置为0.4。

由轨迹跟踪所得气动力加速度，进行气动特征参量αVTC的提取，通过气动特征参数拟合结合动力学方程，实现数值积分条件下的轨迹时序预测[5]，并同本文方法进行对比。

4.2 轨迹跟踪仿真结果及分析

在第4.1节设置的仿真条件下，得到位置估计结果如图9所示。进行20次跟踪统计，并将本文方法得到的位置、速度、加速度的估计均方根误差同CKF、AGIMM-CKF、AGIMM-ACKF方法得到的结果作对比，结果如图10～12所示。

图10 位置估计均方根误差对比Fig.10 Root mean square error comparison of position estimation

图11 速度估计均方根误差对比 Fig.11 Root mean square error comparison of speed

图12 加速度估计均方根误差对比Fig.12 Root mean square error comparison of acceleration

表2给出了四种跟踪方法的位置、速度、加速度均方根误差的均值。对比分析可知，依次引入AGIMM、渐消因子对位置、速度、加速度的跟踪精度有显著提升，引入修正的Markov概率转移矩阵进一步显著减小了位置估计误差均方差。图10～12为多次打靶误差标准差分布图，在自适应网格、渐消因子、修正Markov概率转移矩阵三次改进措施下，机动模式突变的55 s、70 s等时刻的误差标准差峰值逐渐降低，表明改进措施提升了滤波方法鲁棒性。

表2 四种跟踪方法的精度对比Table 2 Comparison of accuracy between four tracking methods

4.3 轨迹预测仿真结果及分析

通过第4.2节跟踪仿真得到的目标状态估计、各机动模型的概率分布、基于似然函数的自适应网格处理得到的模型集参量等进行控制参数的求解，更新的参数包括D-V剖面、H-V剖面以及侧向边界等。在此基础上，利用数值积分方法进行轨迹的实时预示，仿真结果如图13～16所示。

对比图13和图14可知，本文所设计的基于自适应网格的机动模式自适应方法，能够将未包含纵向标称轨迹在内的模型集参数逐步修正至真实机动模型参数两侧。由于轨迹预测是一个随飞行进程不断进行的过程，故选取了36 s,56 s,76 s三个时刻轨迹预测的偏差如图15所示。在引入本文方法前，预测误差呈逐步发散的趋势；加入该方法后，各机动模型预测偏差随预测时间呈先增大后减小的收敛趋势。此外，如图16所示，基于气动特征参数拟合的轨迹预测方法虽然轨迹预测初始误差较小，但在目标机动模式变化后，本文所提基于飞行任务的轨迹预示方法预测误差远小于该方法。

图15 不同起始时刻的轨迹预示误差对比Fig.15 Comparison of trajectory prediction errors at different start times

图16 两种方法预测轨迹对比图Fig.16 Comparison of two methods to predict trajectory

针对轨迹预示过程中存在的多种由机动模型产生的轨迹簇，对预示轨迹概率显著的9种机动模型、概率最大的机动模型以及基于气动特征参数拟合外推方法的预示轨迹分别进行误差统计，统计结果见表3。

表3 轨迹预测误差对比Table 3 Trajectory prediction error comparison

在跟踪预测初始阶段，各机动模型轨迹预测误差逐渐增大，最终达到12 km；但随着机动模式辨识、轨迹预测算法的进行，在46 s,56 s,66 s,76 s概率较大的9个机动模型轨迹预测偏差全程依次位于3.1 km,1.89 km,1.48 km,0.73 km以内；概率最大的机动模型全程轨迹预测误差均值依次为824.9 m,630.6 m,372.3 m,277.8 m，远低于仅依赖气动特征参数拟合的轨迹预测方法，表明所提轨迹预示方法具有更高的精度。