航天器姿态控制输入饱和问题综述

王靓玥，郭延宁，马广富，刘魏林

(哈尔滨工业大学控制科学与工程系，哈尔滨 150001)

0 引 言

随着空间技术的不断发展，航天任务变得愈加复杂化、多样化，从早期任务单一的技术实验验证卫星到目前任务多样明确的各种空间应用卫星，如导航卫星、遥感卫星、气象卫星等。同时，随着任务需求的提高，空间大型挠性附件、在轨服务机械臂、复杂多样的有效载荷等装置的逐渐部署使得航天器的结构日趋复杂，给航天器平台的设计带来了诸多约束与挑战。

航天器姿态控制系统作为航天器平台的一个重要分系统，是航天器能否完成设计任务的关键一环。为高效准确地成功完成任务，对航天器姿态控制系统的设计提出更高的要求。1) 高可靠性：航天器研发成本巨大，设计寿命长，因此首要保证姿态控制系统的高可靠性性能，要求其具有故障诊断和重构的能力。2) 高精度：航天器姿态的指向精度是评价其姿态控制律的重要指标，新型定向卫星的指向精度要求已高达角秒级。3) 高敏捷性：对于进行大范围扫描的观测卫星，姿态机动的敏捷性决定了其观测范围和使用效率。4) 强鲁棒性：难以测量的干扰力矩、内外部参数不确定性以及敏感器和执行器的安装误差等因素的影响要求航天器姿态系统具有强鲁棒性。5) 高稳定度：对于光学遥感卫星，其运动部件的转动和挠性结构的振动会降低成像的质量，因此要求卫星具有高稳定性。

航天器姿态系统的设计是一个经典但又十分复杂的问题，涉及系统敏感器、执行机构等硬件的选型配置，以及姿态确定算法、姿态控制算法的设计优化。仅针对姿态控制算法而言，又包括了控制输入饱和[1]、系统状态受限[2]、系统状态不可测[3]、参数不确定性[4]、干扰抑制[5]、通信时延[6]、快速稳定[7]、容错控制[8]等一系列问题。特别地，在实际任务中，由于作为航天器执行机构的控制力矩陀螺、反作用飞轮以及反作用推力器的物理限制，航天器姿态控制系统中不可避免地存在输入饱和问题。如果在控制律设计过程中未考虑输入饱和情况，则对于未触发饱和约束的姿态调节控制而言，其性能并无差异，但是对于需要较大控制力矩的姿态机动、快速捕获、姿态跟踪以及轨控期间的姿态保持等任务，则可能导致实际施加到航天器的控制力矩不能在给定时间内完成既定姿态控制任务，甚至造成系统失稳的严重情况。

针对控制输入饱和问题，国内外学者已经展开了大量研究，并取得了丰富的研究成果。本文对目前公开发表的航天器姿态控制领域输入饱和问题的文献进行分类整理，将输入饱和的解决技术途径总结为以下三类，如表1所示：1) 控制律整体考虑饱和：该方法是指首先在不考虑输入饱和的情况下进行姿态控制律的设计，接着通过某种方法对所得控制量进行饱和约束，使其满足输入饱和的要求。常见的方法有：饱和函数法[1-2,9-13]、限幅函数法[14-23]、切换函数法[24-25]、抗饱和控制[4,26-31]等。2) 控制律各项分别考虑饱和：姿态控制律是由若干项叠加而成，若控制律中的每一项均满足某幅值约束，则通过对各项系数的选取，即可使得控制律整体满足给定输入饱和的要求。常见的设计方法有：类PD控制[3,5,32-39]、反步法[40]等。3) 考虑饱和约束的优化[41-45]：最优化方法中的时间/能量等最优控制在初末条件等约束下，得到某种性能指标最优解。本文将分别对三类技术途径中的各种方法进行详细阐述，总结分析其设计思想、工作原理、特点、效果效用及适用范围等内容。

表1 常见解决输入饱和问题方法总结Table 1 Summary of usual methods solving input saturation

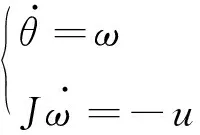
1 航天器姿态控制输入饱和问题

根据刚体复合运动关系，建立刚体航天器姿态运动学方程[46]。利用3-1-2转序欧拉角描述航天器的姿态运动学方程为

(1)

式中:θ=[θ1,θ2,θ3]T表示航天器本体系相对于参考系(可以为惯性系、轨道系等)姿态角，ω=[ω1,ω2,ω3]T为航天器参考姿态角速度，Rbo为本体系相对于参考系的3-1-2转序的方向余弦矩阵，ωd为参考系中的期望角速度，视航天器任务而定，矩阵A为

利用四元数描述的航天器运动学方程为

(2)

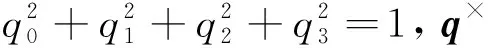
根据刚体的动量矩定理定理，有刚体航天器的姿态动力学方程如下所示[46]：

(3)

式中:J为航天器转动惯量矩阵，u=[u1,u2,u3]T表示航天器的控制力矩，d表示环境干扰和模型不确定性等所有的干扰力矩。

在实际的航天器系统中，执行机构的物理限制导致航天器控制律存在输入饱和问题。总的来说，根据执行机构特性不同，控制输入饱和分为三种：

1) 三轴控制力矩矢量幅值饱和：如采用具有近似球形力矩包络的五棱锥构型控制力矩陀螺群情况，其对应数学描述为

(4)

式中:umax为最大力矩幅值。

2) 三轴控制单轴幅值饱和：如在每个轴安装对应的反作用力矩推力器或反作用飞轮等情况，其对应数学表达式为

|ui|≤uimax(i=1,2,3)

(5)

3) 复杂控制力矩包络：由于执行机构安装构型、环境约束等导致的不属于以上两种情况的力矩约束，比如金字塔构型控制力矩陀螺群、并非沿坐标轴安装的斜装飞轮或者反作用推力器、由于磁场约束带来的磁控力矩约束为圆盘面等。

其中无论执行机构安装构型如何，出于简单考虑，工程应用一般考虑第二种情况以实现单轴解耦控制，对应的研究成果也最多。第一种约束条件也可以通过控制律设计实现，但相对成果较少。此外，即使对于第二种简单饱和约束情况，已有文献证实时间最优控制还需要通过数值优化求解得到的若干次控制切换完成[44]。因此，无论以上任何约束情况，如果要充分发挥执行机构最大能力，都需要最优化方法。

由于在轨计算机计算能力有限，而姿态控制任务一般要求较高的实时性和可靠性，因此已有研究主要针对的是第二种输入饱和问题，即单轴幅值分别受限问题的解决技术途径进行研究。为了更加直观地对比已有的处理输入饱和约束方法的基本原理和工作特性，本文假设各个单轴的幅值限制相同，不考虑干扰力矩情况下，有简化的单轴解耦的航天器姿态运动学、动力学方程如式(6)所示：

(6)

式中:θ为单轴的航天器姿态角，ω为单轴姿态角速度，u为单轴的控制力矩。亦可将单轴的姿态运动学写成四元数形式。

有关针对第一类和第三类约束的更多详情，请参考相关最优化方法的研究进展。

2 控制律整体考虑饱和

该类解决技术途径是指采用合适的控制方法设计未考虑输入饱和的控制指令，然后借助某种限幅方法对该控制指令进行限幅处理，确保最终的控制指令满足饱和约束。

2.1 饱和函数法

饱和函数法是指将执行机构最大力矩幅值作为饱和函数的幅值约束条件，通过饱和函数后的控制律输出满足饱和约束。具体分为直接法和间接法两种方式。

2.1.1直接法

直接法是指直接在设计的姿态控制律外引入sat饱和函数以满足控制输入饱和约束[1,9]。该方式采用最简单直接的方式“暴力”地解决了输入饱和问题。并且，能够在对未触发饱和约束的控制不产生影响的前提下最大程度的利用执行机构的控制能力。然而，该方式在稳定性证明时通常只能保证控制律未考虑饱和约束前的系统稳定性。在不考虑控制与干扰力矩的情况下，由于航天器本身为保守系统，因此对于多数的姿态调节任务而言，并不会导致航天器失稳等恶劣后果。

2.1.2间接法

间接法[2,10-13]在控制律设计时已考虑了限幅后控制律的稳定性。该方式同样能够充分发挥执行机构的控制能力，并且能够通过理论证明保证系统全工况下的稳定性(当然，一般仅针对有初始误差的姿态调节或静止到静止的姿态机动任务)，但设计及证明过程较为复杂。典型设计步骤为首先设计未考虑输入饱和的控制律，并设计某一李雅普诺夫函数，将限幅后的控制律代入。为保证满足李亚普诺夫稳定性，在限幅前控制律中增加自适应参数项，并进一步对李雅普诺夫函数进行增广，通过设计合适的自适应律以及选择合适的控制参数，在假设系统未考虑饱和约束前控制律不会无限大等合理条件的前提下证明了限幅后控制律的稳定性。

2.2 限幅函数法

由于描述执行机构实际物理限制的饱和函数为不连续可微、非光滑函数，饱和约束处的导数不存在。因此，人们提出了多种分段可微或全局可微的光滑限幅函数作为替代，与饱和函数相比，本方法不仅能满足实际饱和约束，还为控制律设计与分析带来极大便利。为了对常见的限幅函数有一个较为清晰直观的认识，图1将其综合绘制在同一坐标轴内。由图1中可以看出，改进饱和函数限幅的曲线与饱和函数最为接近，是对航天器执行机构输入饱和最贴近的描述。

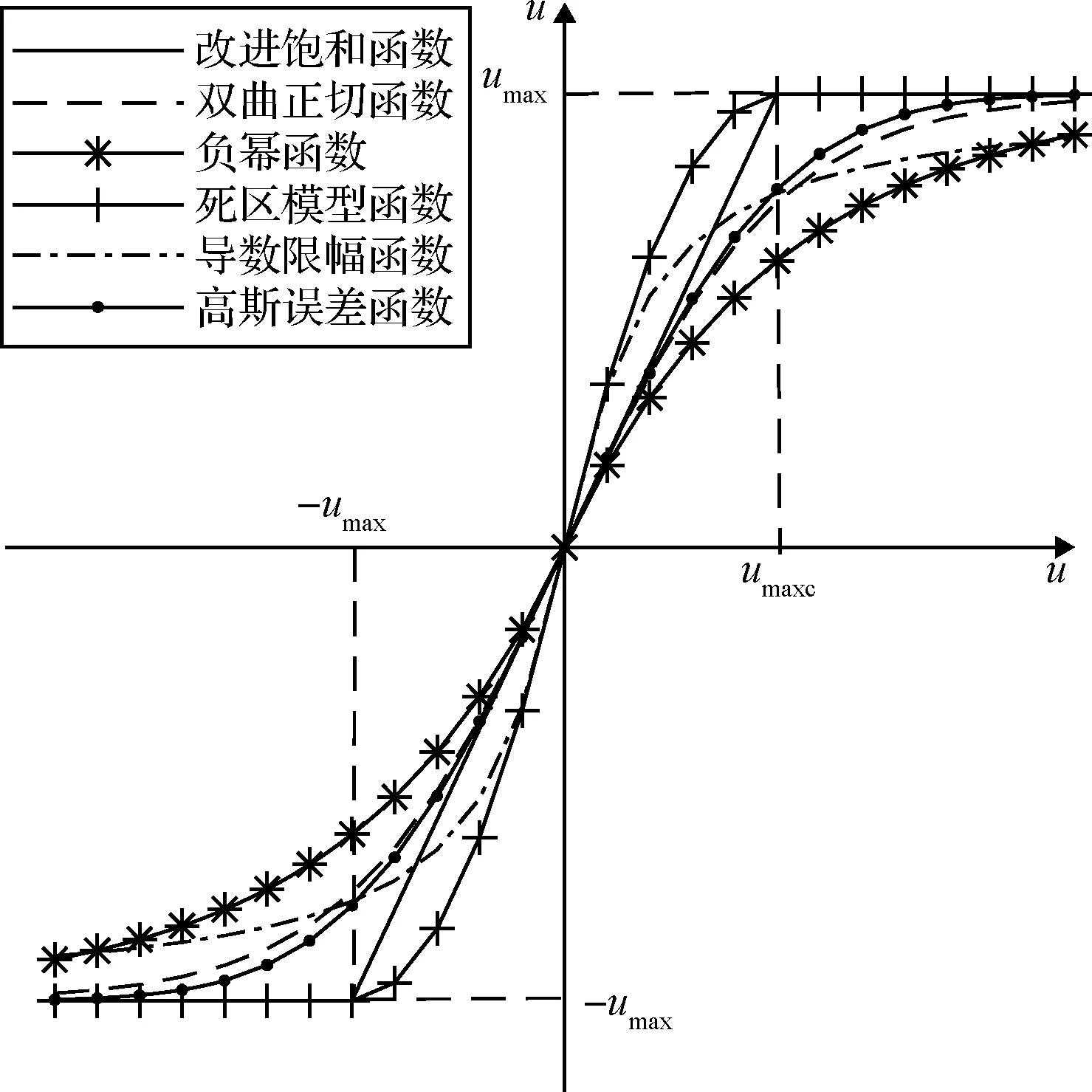
图1 常见限幅函数曲线图Fig.1 Curve of usual limiting functions

2.2.1改进饱和函数

改进的饱和函数[14]利用tanh函数在幅值约束的极小领域附近与sat函数的接近性，使得改进饱和函数足够近似实际饱和约束。其具体形式如下式(7)所示

u=

(7)

式中:参数a为一极小正数，用于保证改进饱和函数的分段可微性。uc为限幅前设计的控制律。umax为最大力矩幅值。

该限幅函数为一个分段可微函数，其限幅具体程度可跟随参数a调节，十分接近实际限幅。同时，其不影响饱和约束前的控制大小。

2.2.2双曲正切函数

利用双曲正切函数[15]进行饱和约束的具体形式如下所示：

(8)

双曲正切函数利用了函数值域本身进行限幅，全局可微，限幅函数为固定形式且削弱了饱和约束前的控制。到达饱和约束后的输出值略小于实际饱和幅值，且随着输入的增加，输出能够较快地无限接近于实际幅值，能够较为充分的利用执行机构的输出能力，属于过限幅类型。

2.2.3负幂函数

负幂函数[18]进行约束的数学表达式如下所示：

u=sgn(uc)umax(1-exp(-sgn(uc)uc/umax))

(9)

负幂函数同样利用函数值域进行限幅，全局可微，限幅函数为固定形式且削弱了饱和约束前的控制。但饱和后的输出明显小于实际饱和幅值，过于保守，执行机构利用率较低，属于强限幅类型。

2.2.4高斯误差函数

高斯误差函数[19]进行幅值约束的形式如下式所示：

(10)

高斯误差函数同样利用函数值域进行限幅，其工作特点以及限幅作用基本同双曲正切函数相同，同属于过限幅类型。

2.2.5导数限幅函数

导数限幅函数[20]利用导数为负则函数值递减，导数为正则函数值递增的性质完成饱和约束。具体形式如下：

(11)

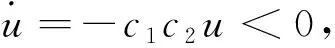
导数限幅函数可以通过参数调节进行变化，全局可微。到达饱和约束前经过导数限幅函数的控制先增强后削弱，且属于强限幅类型。

2.2.6死区模型函数

死区模型函数[21]利用死区性质进行限幅，数学表达式如下：

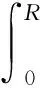
(12)

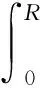
死区模型函数是一个全局可微，参数可调的限幅函数，其使得饱和约束前的控制增强，到达饱和约束后的控制与实际限幅接近。

2.3 切换函数

切换函数[24]解决输入饱和问题的设计思想为令限幅后的控制律仅在饱和力矩幅值之间切换。在不考虑饱和约束情况下，通过系统状态量及其组合设计控制律得到控制指令uc，然后引入同uc符号一致的饱和控制力矩指令作用到航天器。其数学表达式为：

u=umaxsgn(uc)

(13)

对于航天器姿态控制系统来说，该方法通常与滑模变结构控制相结合，比如未考虑饱和约束设计的控制指令可以是由航天器姿态和姿态角速度构成的滑模面。当然，多数情况下，线性滑模面的构造一般等同于PD控制。

切换函数法的优点是能够最大程度利用执行机构的力矩输出能力，对于需要快速姿态机动或跟踪的系统而言，其控制速度非常快。然而，无论系统状态如何，控制力矩幅值均相同，因此不能对于不同的系统状态进行针对性设计。此外，当系统抵达所设计的滑模面(或uc接近0)时，过大的控制力矩导致了系统状态在滑模面或平衡点附近高频抖动，即抖振现象。高频的切换指令在实际任务不仅难以实现，还可能激励太阳帆板振动或液体燃料晃动，使得此类控制律不能直接应用。

针对上述抖振问题，可以引入边界层的概念对式(10)进行改进[25]，改进后的控制律如下所示。

u=umaxsat′(uc)

(14)

式中

式中:Δ即称为边界层，其幅值的大小影响着系统的抖振强弱和控制性能。边界层越大，切换次数越少，抖振的抑制能力越强，但系统的响应速度越慢。绘制改进前后切换函数描述如图2所示。

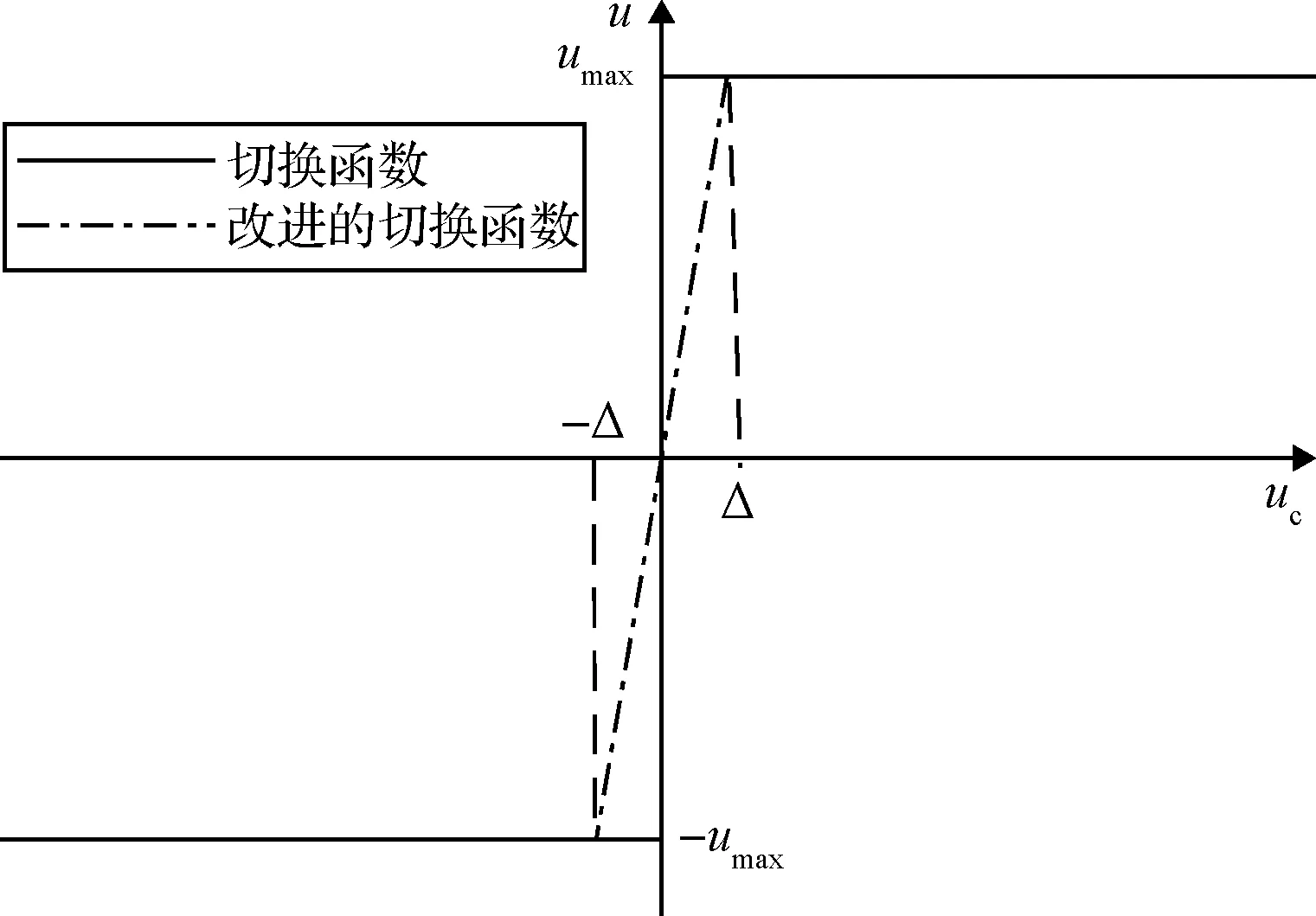
图2 改进前后切换函数曲线图Fig.2 Curve of switching function and improving switching function

2.4 抗饱和控制

考虑输入饱和后作用到航天器实际控制力矩和按照性能指标要求设计的控制力矩不相同，从而使得航天器系统的性能不能按照预定的规律变化，影响系统的控制效果。为削弱输入受限对控制性能的影响，在饱和函数、限幅函数等解决输入受限方法的基础上引入抗饱和控制，以获得更佳的控制效果。

抗饱和控制的工作机理为将限幅前后的控制力矩作为输入，通过抗饱和模块进行处理，将其输出反馈到控制器，即在控制器中增加抵消输入饱和影响的控制项，原理图如图3所示。当然，如果原有控制器输出的控制指令并未触碰限幅函数边界，则抗饱和模块的输出也为零。

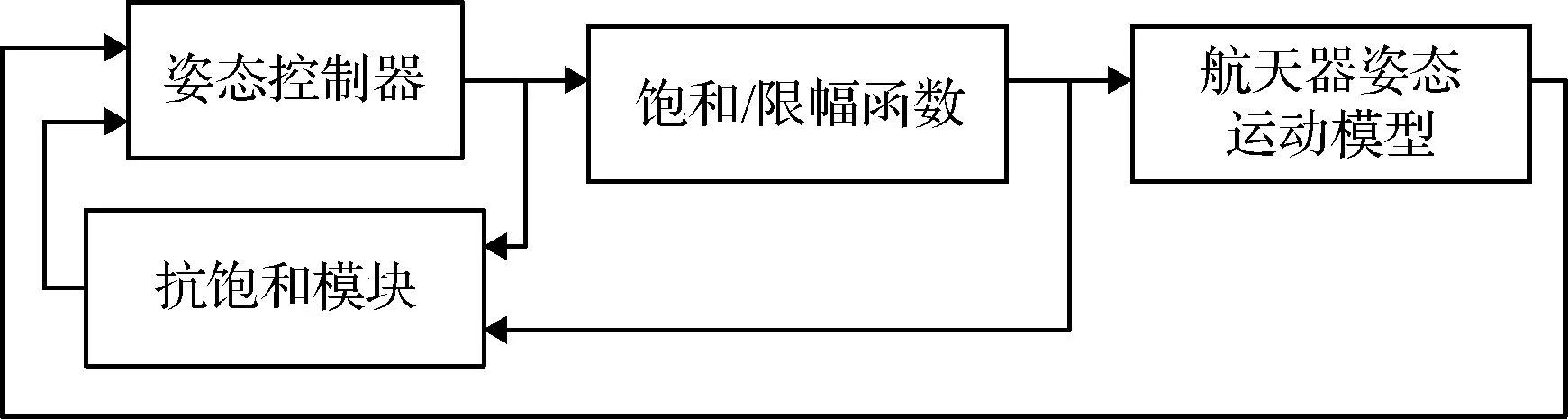
图3 抗饱和控制原理图Fig.3 Theory of anti-saturation control

常见的抗饱和模块设计方案有：

1) 神经网络[26]：利用神经网络对非线性的逼近特性，设计合适的网络作为抗饱和模块，通过对网络的训练，使得神经网络的输出可以削弱输入饱和对控制系统的影响。

2) 干扰观测器[28]：将输入饱和对控制力矩的影响视为系统的一种干扰，通过设计干扰观测器，对前后差值进行估计后并将估计值反馈到控制器中。

3) 抗积分饱和][29]：饱和现象往往是由于控制器中所含的积分环节引起，故抗积分饱和的工作原理是对限幅函数前后控制力矩之差的积分作为反馈信号构成负反馈之路进行抗饱和处理。

4) 辅助系统[30]：即定义辅助变量，并在控制律中引入辅助变量，通过设计辅助变量更新律的设计实现抗饱和。

2.5 特点及应用总结

控制律整体考虑饱和能够充分利用执行机构力矩输出能力，换言之，在控制过程中该技术路径产生的实际控制指令将会到达并保持在饱和幅值。控制律从形式上能够显然地满足饱和约束，结构简单，意义明确。然而，饱和约束、有界干扰以及航天器三轴耦合等因素导致在采用该技术途径设计控制律时需要引入自适应律或限定控制系数的范围以保证系统的稳定性。最终设计的控制律形式较为复杂，系数选取受限，计算量较大。

饱和函数直接法虽然在多种实际任务中能够使得系统状态趋于稳定，但是尚缺乏有效统一的稳定性证明，甚至对于部分超出执行机构控制能力的快速跟踪任务而言，根本不能证明。而饱和函数间接法和限幅函数法在构造李雅普诺夫函数时常常引入了除状态变量以外的自适应项，所以该李雅普诺夫函数单调递减并不等价于航天器状态的渐近收敛，当然这也是为了满足各种实际问题不得已作出的妥协。同时，在稳定性证明时需要考虑姿态动力学模型中输入的控制与直接设计的控制的差值，在假定差值不会无限大的前提下，通常将控制律改写为类似线性或未考虑饱和约束的控制加限幅补偿的形式进行后续证明。

采用该技术途径设计的控制律能够较为充分的利用执行机构的输出能力，相应调节时间短，但形式复杂，计算量较大，适当调节参数情况下，适合对任务时间有一定要求、计算能力强的航天器姿态快速机动等任务。同时，对航天器的控制精度和性能有一定标准的任务，可采用该技术途径与抗饱和控制相结合的控制方法，以补偿超出饱和约束的部分，削弱对系统控制系统的影响。

3 控制律各项分别考虑饱和

这类方法的设计思想是利用系统某些状态本身或状态函数有界的特性使得控制律中的每一项均满足某一幅值限制。并且通过对各项控制系数的选取，设计的控制律在系统的任何状态下都能满足饱和约束。

3.1 类PD控制

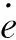
(15)

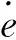
表2 类PD控制中常见的比例项和微分项形式Table 2 Usual proportional and differential terms in PD like control

|uc|≤Kp+Kd

(16)

因此，可以根据Kp+Kd≤umax的原则，选择控制系数Kp和Kd。

3.2 反步法

反步法[40]是一种递归设计方法，通过递归地构造闭环系统的Lyapunov函数设计保证系统稳定性的控制律。对于航天器姿态控制问题，反步法依次构造姿态稳定Lyapunov函数、姿态角速度稳定Lyapunov函数(包含姿态稳定Lyapunov函数)，并利用Lyapunov直接法分别设计虚拟控制律以及姿态控制律。解决输入饱和的原理是利用三角不等式|a+b|≤|a|+|b|，使得控制律中的各项分别满足某一幅值限制，通过控制律中控制系数的选取，使得控制律满足饱和约束。

根据上述思想，利用反步法解决输入饱和问题的单轴控制律的一般形式如下式(17)所示[40]：

(17)

式中:g>0，ωs为虚拟姿态控制律，Ω(·)为一类κ∞函数。即Ω(·)严格单调递增，且满足Ω(0)= 0，Ω(∞)= ∞。其通常选取为Ω(x)=ηx,η>0的形式。

虚拟控制律的设计既要保证航天器的姿态稳定性，又要满足单项幅值受限的约束。当选择四元数描述方式时，可以设计为比例控制，即ωs=-sq；当利用其它描述方式时，即可利用反正切函数等函数设计如ωs=-αarctan(βθ)等满足饱和约束的形式，式中，α>0,β>0。

当设计虚拟控制律为ωs=-sq，Ω(·)函数为Ω(x)=ηx,η>0时控制律如下式(16)所示

(18)

式中:e=ω-ωs

利用三角不等式对控制律进行缩放，并结合|q|≤1的性质，得到式(16)的控制律幅值满足如下约束(具体推导详见文献[40])：

(19)

式中:|e|≤max[|e(t0)|,1/(2g)]。

因此，可根据系统的初始状态，合理选择控制参数g,η,s，使得控制律满足饱和约束条件。

3.3 特点及应用总结

控制律各项分别考虑饱和约束能够保证设计的控制律在任何状态下均能满足饱和约束。稳定性证明同整体考虑饱和相比较为容易，设计简单。然而，由于各项函数限幅和三角不等式缩放等因素，推导过程过于保守，不能有效发挥执行机构力矩输出能力，其控制力矩在大多数正常工况下通常远小于约束幅值，仅在系统状态或状态函数等变量达到边界等极值情况才能饱和。因此，在控制系数满足要求的同时需要合理，使其能够在常见工况下充分利用输出能力。故控制律各项分别考虑饱和得到的控制律适合于对调节时间无明确要求的航天器姿态控制任务或者低成本小卫星简化任务。

4 考虑饱和的优化方法

4.1 方法介绍

考虑饱和约束的优化方法[41-45]不是一类专门解决输入饱和问题方法，其在设计如时间等某项性能指标最优控制律的过程中，考虑包括输入饱和在内的多种控制及状态约束。因此，通过某种解析或数值解法求解出的控制指令能够满足饱和约束。

该方法不仅仅能够有效解决航天器三轴单轴幅值的输入饱和问题，针对三轴矢量幅值[47]以及复杂控制力矩包络[48]输入饱和问题同样能够合理处理。并且，该方法在解决输入饱和问题的同时还能够处理多种复杂的状态约束[49]。

以时间最优控制为例对这种方法进行说明。时间最优控制是一种以获得最短控制时间为目的的控制律设计方法，而输入饱和约束作为其中的一项约束。其数学描述为如下:

考虑约束条件：

(20)

求解控制律u使得如下性能指标到达极小值

(21)

式中:x(t)为航天器系统的状态：姿态和姿态角速度，t0和tf分别为开始时刻和结束时刻。

时间能量最优控制同样是一种可以满足输入饱和约束的最优化问题，其性能指标一般为

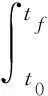
(22)

利用极小值原理或动态规划等方法对上述问题进行求解，可得满足输入饱和约束的最优控制指令。

4.2 特点及应用总结

考虑饱和的优化方法可在考虑多种状态及控制约束的情况下得到时间/燃料最优解，并且容易应用于末端角速度非零的航天器姿态机动任务。由于求得的控制律往往为数值解，计算量较大，并且依赖精确的航天器数学模型，因此适用于已知精确模型且对于时间、燃料等参量具有最优性能需求的航天任务。如大型航天器的最优姿态机动等。目前，如ISS[50]等大型卫星已采用地面离线优化及在轨跟踪算法结合的方式完成航天器姿态机动任务，在满足状态及控制约束的情况下完成时间最优控制。虽然当前的优化方法多为地面进行并上传到在轨航天器，但可以预见的是，随着航天器自身计算能力的不断提升，该方法未来将具有巨大的应用前景。

5 结束语

航天器控制输入饱和问题至今已被较为深入广泛的研究，本文对现有文献解决输入饱和问题的方法进行分类总结，分为控制律整体考虑饱和、控制律各项考虑饱和以及考虑饱和的优化方法三类，并分别系统地对这三类方法进行详细的梳理，阐述其数学形式，分析设计思想，总结工作特征。得到控制律整体考虑饱和适合对任务时间有一定要求、计算能力强的航天器姿态快速机动等任务。控制律各项分别考虑饱和由于过于保守仅适用于对调节时间无明确要求的航天器姿态控制任务或低成本小卫星简化任务。已知精确模型且对于时间、燃料等参量具有最优性能需求的航天任务通常选用考虑饱和的最优化方法。航天器输入饱和问题是实际航天器任务中不可避免的问题，因此针对输入饱和问题的研究需要不断完善，可以在采用控制律整体考虑饱和时如何在保证稳定下的前提下简化控制律的形式；在采用控制律各项分别考虑饱和时，如何更为有效地利用执行机构的输出能力等方面进行深入研究，以更好地为实际任务提供有效的理论支撑,令设计的算法在工程实际中得到应用。