基于磁链优化模型的感应电机转子时间常数辨识

赵 云，蔡美东，聂雅萍，王晓光

(湖北工业大学 太阳能高效利用及储能运行控制湖北省重点实验室，湖北 武汉 430068)

要想提高感应电机间接转子磁场控制系统的控制精度，就必须准确获取转子时间常数Tr(Tr=Lr/Rr)。尽管在电机运行前采取各种方式对Tr进行离线测量，但在电机运行时，Tr与转子电阻、转子电感有关，其中转子电阻受到温度等因素影响，而转子电感受到电机磁场影响[1-2]。Tr的不准确，会使转子磁场定向出现偏差，导致电机输出转矩不能得到准确控制，因此在线辨识Tr是非常必要的。

在众多Tr在线辨识方法中，基于模型参考自适应(model reference adaptive system，MRAS)的Tr辨识方法由于较低的运算量和较高的性能而受到广泛关注[3]。在感应电机Tr辨识中选择不同的模型，可以构成不同的MRAS系统。文献[4]基于转子磁链q轴分量模型构成辨识系统，采用电压模型获取q轴的转子磁链，实现Tr辨识，但该方法需要获取定子电压，会受到死区效应的影响。文献[5]为了实现d轴电压模型在工程上的应用，考虑了定子电阻、死区效应补偿方案来提高Tr的辨识精度，但忽略了转子电感对Tr的影响。文献[6]采用电磁转矩模型来辨识Tr，但辨识系统存在错误平衡点，使得其仅适用于电机重载工况。文献[7]提出一种基于无功功率模型的Tr辨识算法，并验证了该模型的稳定性，但该方法不适用于四象限运行辨识区间。文献[8]采用转子磁链和定子电流的点乘模型的Tr辨识方法，解决了死区效应的影响，但该方法需要转子磁链，而磁链观测中的纯积分运算又存在直流偏量的问题。为此，文献[9-10]计算了定子磁链中的直流分量，并采用反馈PI控制来抑制观测磁链的直流偏量，但是输出磁链的直流分量仍不能完全抑制。文献[11-12]把纯积分器换成低通滤波器，能很好地抑制直流分量的问题，但低通滤波器的存在会导致磁链幅值、相位产生偏差。

为了解决纯积分问题对定子磁链观测的影响，本文研究一种基于直流偏量双闭环的方案去优化磁链观测器，并采用优化后的磁链观测器与定子电流和定子磁链的点乘模型，实现感应电机Tr的在线辨识。

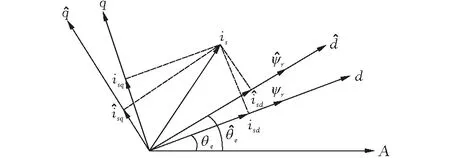
1 转子时间常数不准确对磁场定向的影响

在感应电机间接磁场定向控制系统中，磁场定向角θe观测模型如图1所示[13]。

图 1 磁场定向角观测模型

当磁场处于稳态时，微分项为零，则磁场定向角θe可表示为：

(1)

2 转子时间常数的在线辨识方法

2.1 感应电机数学模型

在d、q轴同步旋转坐标系下，感应电机动态数学模型[14]如下：

(2)

(3)

(4)

(5)

稳态时，公式(3)的微分项为零，并将式(3)和式(5)代入式(4)中可得到稳态的定子磁链，进而求得其表达式：

(6)

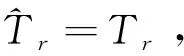
(7)

2.2 基于定子电流和定子磁链点乘的Tr在线辨识方法

图3给出了基于定子电流和定子磁链点乘的Tr辨识实现框图。定子电流和定子磁链点乘的参考模型如式(8)，可调模型如式(9)，自适应率如式(10)，模型偏差ΔM=Mref-Mest，定子电流和定子磁链的点乘值不受坐标系限制，即两相静止坐标系下的点乘值isαψsα+isβψsβ和两相同步旋转坐标系下的点乘值isdψsd+isqψsq相等。

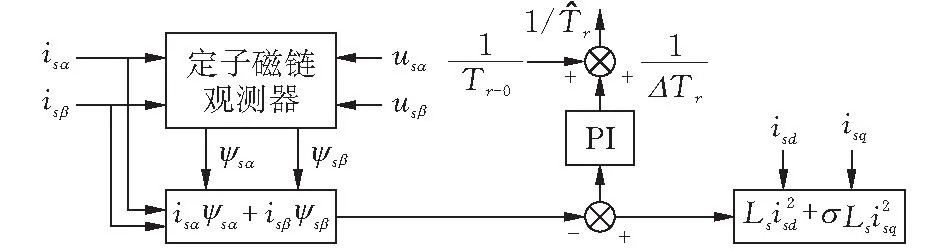
图 3 转子时间常数辨识框图

Mref=isαψsα+isβψsβ

(8)

(9)

(10)

其中Tr-0为初始转子时间常数，ΔTr为转子时间常数偏差的补偿值，Kp、Ki分别为PI调节器的比例系数、积分系数。

将稳态定子磁链式代入式(8)可得：

(11)

在定子磁链观测器中，通常会忽略输入直流偏量的影响，使得磁链的观测值产生偏差，为此设计一种磁链优化模型。

3 磁链优化模型

当忽略输入直流偏量时，稳态下定子磁链与反电动势的关系如下式：

es=jωeψs

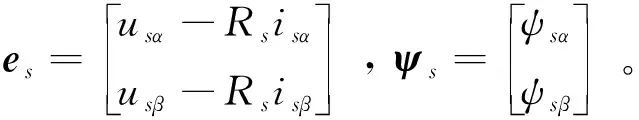
当考虑输入直流偏量时：

因此，为了解决纯积分的影响，消除输入的直流偏量，可设计闭环调节系统，直流偏量Δd经过补偿增益Kd模块在积分器前端进行补偿(图4)。

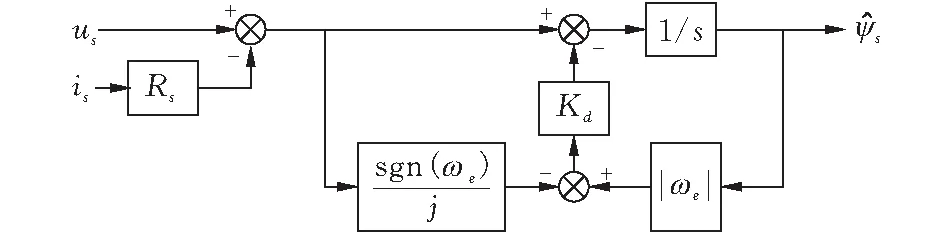
图 4 考虑直流偏量补偿的磁链观测器

由图4得到系统的传递函数如下式：

图5a表示相同定子频率，不同Kd的Gψ0(s)Bode图，取ωe=314 rad/s，Kd分别取0.1、1、10。图5b表示相同Kd，不同定子频率的Gψ0(s)Bode图，取Kd=10，ωe分别取31.4、314、628 rad/s。

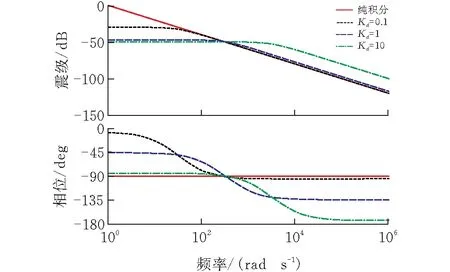
(a)相同定子频率，不同Kd

由图5可知，减小定子频率，磁链观测器的响应速度会变慢，而增大补偿增益Kd会提高磁链观测器的动态性能，但又会降低其对高频噪声的抑制能力。为此将Kd设计成如下式的函数：

其中，ωc为截止频率，通常为所选电机额定频率的5%～20%；C为临界积分系数，通常取1～10。

但上述观测器有一个明显的缺点是消除直流偏量的速度较慢，为此在图4的基础上再并联一条补偿积分模块，优化后的磁链观测器框图如图6所示。

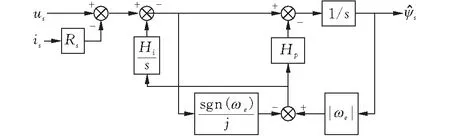
图 6 优化后的磁链观测器

由图6得到系统的传递函数如下式：

当系统处于稳态时，上式可化简为：

由此可知，稳态情况下，优化后磁链观测器的定子频率响应和积分器完全一致，可以完全消除纯积分问题，实现定子磁链准确观测。优化后的磁链观测器实现框图如图7所示。

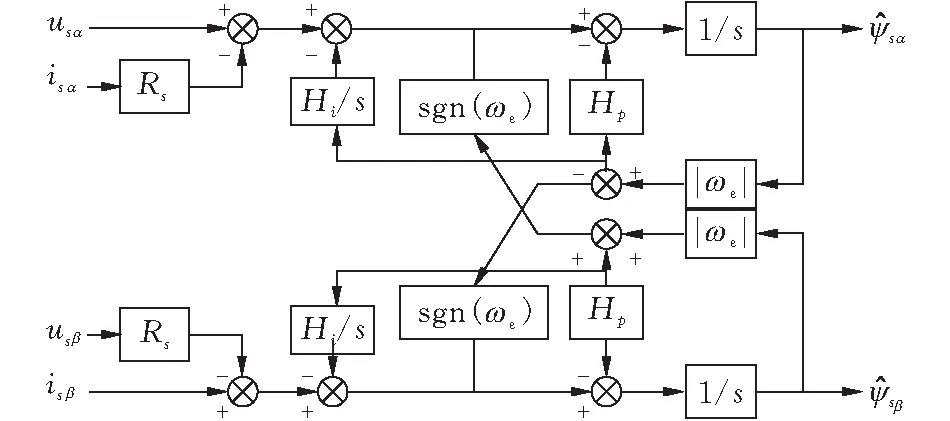
图 7 优化后的磁链观测器实现框图

由图7可知，优化后的磁链观测器含有两个参数：Hp、Hi，其中，参数Hp的选择仍遵循Kd设计思路，Hi可以消除定子磁链直流分量的影响，对参数Hi的设计参考典型二阶系统设计方案，此时可得：

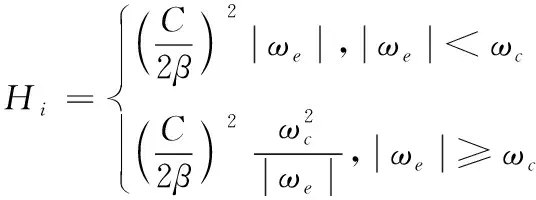
图8给出了优化后的传递函数Bode图，按照上式分别取阻尼比β为1、2、5。可以发现β增大，参数Hi减小。当β增大到无穷大时，Hi减小到0。

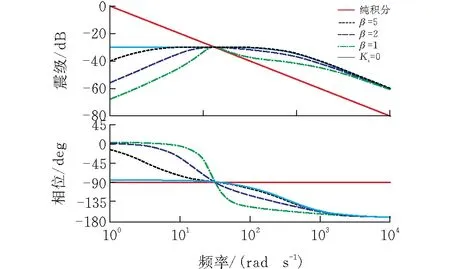
图 8 传递函数Gψ(s)的Bode图

由图8可知，当Hi减小到0时，相当于只存在补偿Kd增益，而伴随着β的减小，参数Hi增大，加快了消除直流偏量的速度。同时减小阻尼比β会在频谱响应图中形成一个凸峰，会造成系统不稳定，因此需要择优选取参数C、β、ωc。

4 仿真研究

基于以上分析，在间接转子磁场定向控制系统中，采用优化后的磁链观测器，在Matlab中建立如图9所示的基于定子电流和定子磁链点乘的Tr在线辨识系统框图。

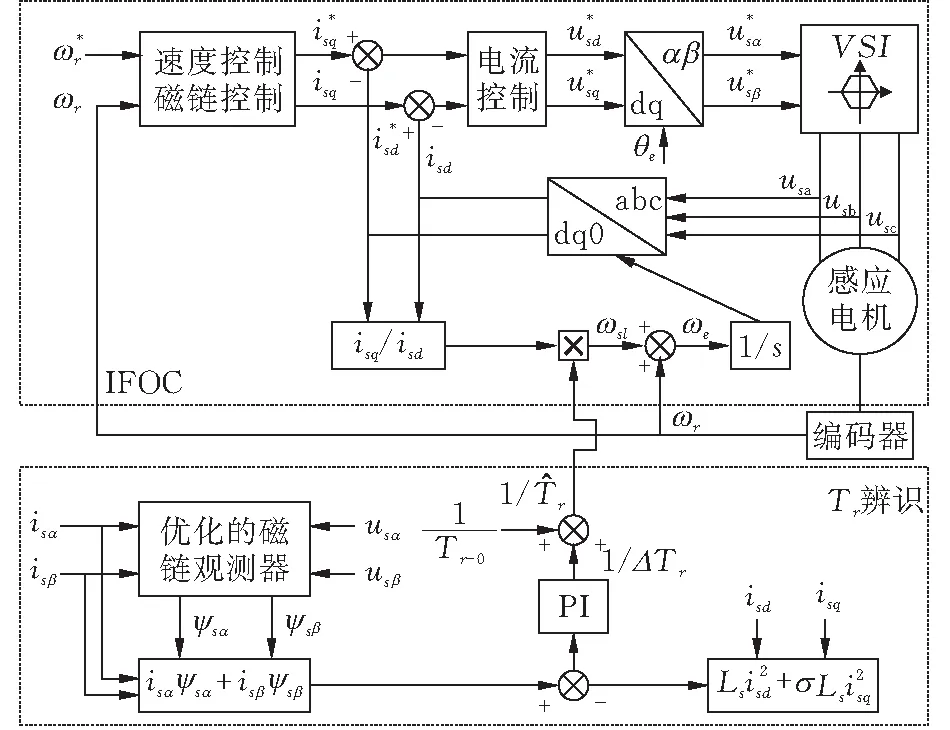
图 9 间接转子磁场定向控制系统框图

仿真所用参数以3.7 kW感应电机参数为参照(表1)。

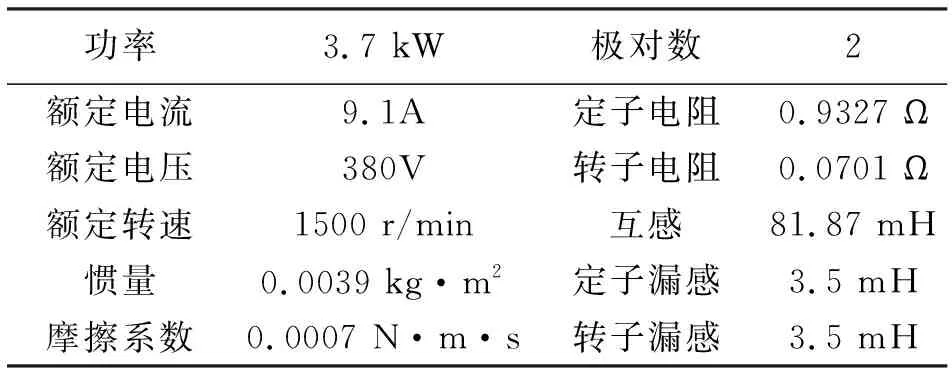
表1 电机参数

从电机参数可计算出

首先对定子磁链观测器进行仿真验证，给定电机转速314 r/s，在0.5 s分别给电压usα,usβ施加1V和-1V的直流偏量电压，图10a、b分别为优化前后定子磁链观测曲线。

(a)优化前

由于积分器的影响，观测的定子磁链中含有直流分量，以至于降低了定子磁链观测精度。如果将图10a中定子磁链观测值直接用于辨识Tr，那么Tr观测值会出现很大的偏差。而图10b中磁链观测值稳态时没有直流偏量，具有更高的观测精度，更适用于辨识转子时间常数。

下面对基于优化后磁链观测模型的Tr辨识方法进行仿真验证，对感应电机施加5 N·m的负载，当电机运行稳定1 s后，启动Tr在线辨识方法。图11a表示初始转子时间常数偏小的辨识结果，图11b表示初始转子时间常数偏大的辨识结果。

图11 转子时间常数辨识结果

从辨识结果可知，当初始转子时间常数为0.08 s时，启动辨识算法，如图11a所示，辨识时间间隔约为0.5 s，最终Tr被修正到0.12 s左右，对于图中出现的明显尖峰，主要是由于PI调节器的系数设置过高的影响，但如果降低PI调节器的系数，削去尖峰，会使得辨识时间延长。当初始转子时间常数为0.16 s时，启动辨识算法，如图11b所示，辨识时间间隔约为0.5 s，最终也被修正到0.12 s左右。所以无论初始转子时间常数偏大还是偏小，在启动辨识算法之后，估计的转子时间常数能很快得到修正。

进一步验证所提出辨识方法的有效性，在磁场定向控制系统中，给定转速1500 r/min，3 s后突加10 N·m负载，4.5 s降低负载为5 N·m，6 s降低转速到1000 r/min，对有无Tr辨识系统分别进行仿真，观测控制系统电机转速和输出转矩响应曲线(图12-13)。

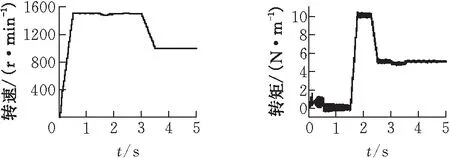
图12 无Tr辨识的转速与输出转矩响应曲线

如图12所示，在磁场定向控制系统中，当不启动Tr辨识方法，电机空载启动，给电机突然加、减负载，都会使电机转速和输出转矩出现较大的波动。如图13所示，在磁场定向控制系统中，当启动Tr辨识方法后，电机的转速和输出转矩响应曲线都比较平稳，具有较好的动态响应效果。

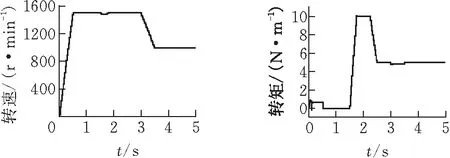
图13 有Tr辨识的转速与输出转矩响应曲线

5 结论

针对Tr不准确造成感应电机磁场定向出现偏差的问题，构造了基于定子电流和定子磁链点乘的Tr在线辨识方法，优化了基于直流偏量补偿的磁链观测器，并利用该观测器准确获取了定子磁链。对该辨识方法的仿真结果表明：该辨识方法准确有效，可改善感应电机间接转子磁场控制系统的性能。