涡流涂层测厚的仿真分析与实验研究

王选择，方诗雪，翟中生1,

(1 湖北工业大学机械工程学院，湖北 武汉 430068； 2 湖北省现代制造质量工程重点实验室，湖北 武汉 430068)

以电磁感应为基础的涡流法测量涂层厚度技术是一种非破坏性、非接触、不需要耦合剂的高效快速无损检测方法。其基本原理是，在测量探头上施加交变电流信号，通过测量探头两端电压信号相对于施加电流信号的变化，来判断探头复阻抗的变化，从而确定材料表面的涂层厚度。在导电导磁材料的表面有着良好的灵敏度，涡流无损检测技术因此用于基体涂层厚度的测量。应用涡流法涂层厚度的测量，激励信号类型的选用与测量信号特征值的选取十分关键。Ulapane N等人提出了一种基于脉冲涡流传感器探测器线圈电压衰减率的铁磁材料厚度量化方法，通过推导衰减率的表达式，建立衰减率与材料厚度之间的关系[1]。王洪波小组提出了一种固定位置涡流传感器测量金属膜厚度的方法，以电信号反应的探头阻抗大小与提离距离之间的斜率关系，来推导某一测量信号下的涂层厚度[2]。Sophian A等人通过对比试验提取信号相应峰值来测量涂层厚度并量化涂层缺陷[3]。为了进一步减少环境对测量数据的影响与提高精度，Ayad A等人引入遗传算法对各项特征值进行优化，提高了测量结果的精度与灵敏度[4]。这些方法一定程度上能够建立特征量与被测对象之间的关系，但对于减率、信号峰值等特征量衰减的提取容易受误差的影响，精确度难以保证。为此，本文建立了正弦激励信号下的涡流技术测量涂层厚度仿真模型，并在稳态下研究线圈探头电压幅值与提离距离之间的关系。

1 涡流法测量涂层厚度的理论基础

1.1 电磁场理论

在COMSOL中分析电磁现象，是利用规定条件的麦克斯韦方程组来进行求解。对于涡流涂层厚度测量实验中的电磁场，仿真分析主要针对涡流线圈探头进行求解，涡流探头中的电磁场可看作时谐电磁场[5]，其微分方程组为：

(1)

其中:H为磁场强度，A/m；Js为外源电流密度，A/m2；ρ为自由电荷体密度，C/m2；B为磁感应强度，1 T=Wb/m2；ε为线圈材质介电常数，F/m；σ为线圈材质导电率，S/m；E为线圈内部电场强度，V/m；D为电位移矢量，C/m2。在激励电流为正弦变化时，这里采用的复数表达形式，既保留了信息完整性，也降低求解的复杂度。

当给予线圈交流电流信号时，根据法拉第电磁感应定律，线圈内部产生交变感应磁场，被测工件内部也产生交变电流与感应磁场，因此在两个磁场空间中会形成叠加磁场从而影响线圈传感器。在线圈内电流一定的情况下，当线圈与被测工件之间距离改变时，线圈内电场强度将发生变化，因此测量线圈两端电压即可反映线圈与被测工件的距离改变量。

1.2 传感模型理论分析

在涡流涂层测厚试验中，可以将涡流传感器的线圈与被测工件作为变压器模型来进行理论分析。将测量探头等效为一个电感与电阻串联，施加特定频率的交流电流激励信号，待测基体及其涂层等效为一个电感和电阻的串联次级电路。模型如图1所示。

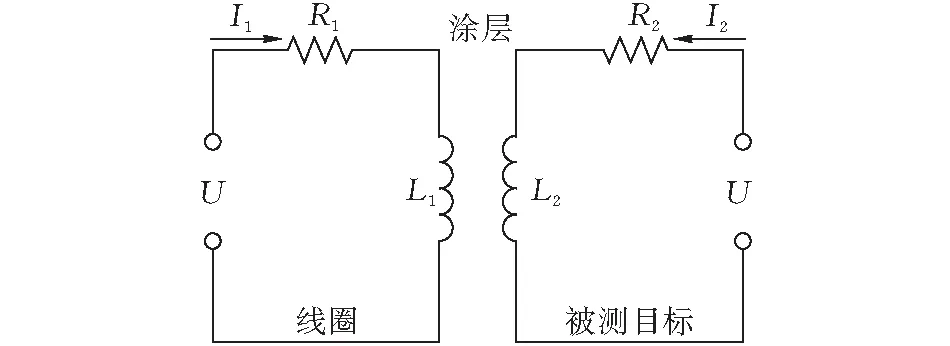
图 1 测量系统等效电路

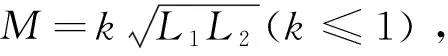
(2)

求解方程可得：

(3)

从而探头线圈阻抗Z的复数表达形式为：

(4)

根据阻抗腐蚀表达形式，可计算探头的等效电感与等效电阻：

(5)

当模拟涂层厚度的间隙发生改变时，探头的等效阻抗也发生改变。通过检测探头两端信号电压值，即可量化探头所获取的涂层厚度信息。

2 仿真建模

2.1 仿真实验设计

在涡流技术的涂层厚度测量实验中，当涂层材质磁导率远小于基体材质并等价于空气磁导率时，假设提离距离为基体表面涂层厚度，仿真实验则可转变为测量提离距离与线圈导体中电信号强度之间的关系。

本研究采用圆柱形线圈，设置被测基体各向同性并没有影响测量结果的缺陷。考虑磁场的对称性，2D模型如图2所示。采用固定频率的正弦电流信号作为激励信号施加在测量线圈上。

图 2 仿真模型

模型中各结构参数与材料特性参数如下：探头线圈外径为10 mm，高度12 mm，线圈匝数为800匝，线圈导线导电率为6×107S/m，横截面积为10-6m2。被测基体为长方体，厚度10 mm，长宽均为80 mm，相对磁导率为4000，电导率为1.12×107S/m，相对介电常数为1；求解提离区域半径为40 mm，相对磁导率为1，相对介电常数为1，导电率为0 S/m。

2.2 仿真实验结果分析

使用COMSOL在磁场(mf)接口下对模型进行频域计算。建立组件参数后，为了验证激励频率对提离距离的影响，选用幅值为200 mA的多个频率正弦电流信号对仿真线圈进行激励；线圈按照0.01 mm步长，从距离基体0 mm处向上移动至0.1 mm；仿真求解线圈的电压大小，并用复数形式表达。

仿真实验使用两步计算，首先模拟在此激励频率下的模拟电感大小，再模拟在此频率下改变提离距离、线圈电压的改变情况。仿真实验结果如图3所示：观察5个激励频率下，随着提离距离的加大，线圈两端的电压降低。在仿真实验范围内，激励频率越高，电压值越大，且电压改变量也越大。因此在高频率激励下具有更高的灵敏度。

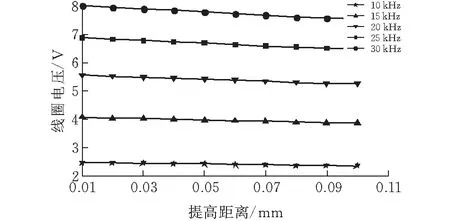
图 3 提离距离与线圈电压的关系

利用最小二乘法采用一元线性拟合分析数据特征，设置U=ax+b，其中x为提离距离，U为线圈电压，拟合结果分别如下：

1)激励信号为10 kHz时，U= -1.282x+2.485，线性相关系数为0.9916；

2)激励信号为15 kHz时，U= -2.348x+4.081，线性相关系数为0.9926；

3)激励信号为20 kHz时，U= -4.504x+6.886，线性相关系数为0.9969；

4)激励信号为25 kHz时，U= -3.436x+5.566，线性相关系数为0.9932；

5)激励信号为30 kHz时，U= -5.472x+8.028，线性相关系数为0.9932。

考虑到实际测量中对信号处理的方便，选取适中的20 kHz作为后续试验的激励频率。对20 kHz激励信号做进一步仿真，按照0.02 mm的步长，测量0.06 ～0.2 mm的提离距离。线圈电压的变化情况如图4所示。

图 4 20 kHz激励频率下提离距离与电压的关系

拟合方程为U= -3.414x+ 5.565，线性度为0.993。因此可以判断，在20 kHz的激励频率下，一次线性拟合能够较好地满足提离距离与线圈电压之间关系。

3 实验验证

为了验证仿真分析的正确性，搭建了正弦激励条件下的涡流法测量涂层厚度的实验。采用涂层标准校准片与铁基校零板作为模拟提离距离与基体。设计差分放大电路提取测量探头两端因提离距离改变而变化的电压信号。通过STM32单片机的DAC模块与DDS技术，产生输出频率可控正弦激励信号，并利用STM32单片机自带两路12位AD模块同步采集探头电压输出信号作为激励信号；最后通过信号处理程序，获取探头输出信号与激励信号之间的幅值比A与相位差φ。考虑到电路中非传感元件参数的影响，相位差必定是一个连续变化量，这里把Acosφ作为信号特征值，代替单纯幅值比，更能体现输出信号的综合效果。

为完成多厚度的测量，将标准试片进行叠用，共测量11种模拟涂层厚度：0、11、23、35、46、49、60、72、84、96、99 μm。按照每一个厚度，取试片上5个不同位置进行测量并求取厚度平均值，同时记录信号特征值。图4显示了涂层厚度与信号特征值之间的关系与最小二乘的线性拟合结果。拟合曲线方程为U= -0.004145x-0.8306，其中U为信号特征值，x为涂层厚度。且相关系数为0.9995。

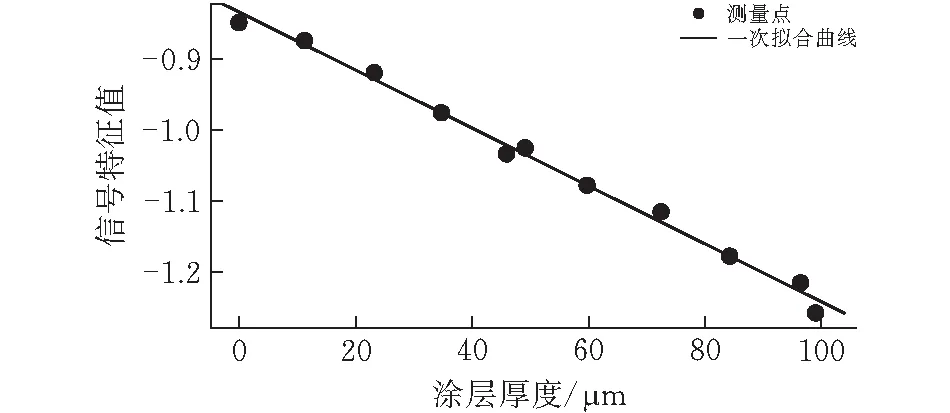
图 5 涂层厚度与信号特征值之间的关系

这里的特征值为负数，是因为在实验中为了去掉基础信号的影响，采用差分放大，导致输出信号与激励信号反向。

从拟合结果来看，所选取的特征值与涂层厚度具有较好的线性相关性。通过测量获取拟合曲线反演涂层厚度误差如图6所示，即在测量范围为100 μm的范围内，绝对误差控制在±3 μm以内。

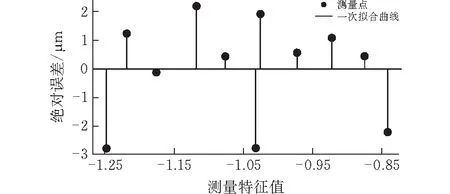
图 6 反演测量值与真值的绝对误差

4 结论

本文利用COMSOL仿真软件对金属基体非金属涂层厚度进行仿真分析，研究了仿真线圈探头两端电压与提离距离之间的关系。结果表明，利用探头输出电压信号的幅值作为特征值与提离距离进行拟合计算有着较高的精度。搭建实物实验平台对仿真模型进行验证，在测量0～99 μm范围内涂层厚度时绝对误差在±3 μm，且利用Acosφ比作为测量特征值时，拟合误差最小，线性度最好，与仿真分析结果一致。实验结果与仿真结果具有高度的一致性，从而验证了仿真理论模型的正确性与可靠性。