基于改进樽海鞘群算法的垃圾邮件分类
2021-02-23刘芳瑞陈宏伟
刘芳瑞,陈宏伟
(湖北工业大学计算机学院,湖北 武汉 430068)
电子邮件给网民提供了便利的方式来传递数据与别人交流,但是,垃圾邮件的泛滥[1]不仅影响用户体验,也带来日益增多的安全风险。
一些邮件文本分类问题已被研究,文献[2]提出支持向量机作为分类器开发了两种策略,以最大可信度分类和统一可信度分类的未标记评论识别垃圾邮件;文献[3]基于词向量间余弦相似度的朴素贝叶斯分类算法广泛应用于机器学习分类问题;文献[4]提出基于统计特征,通过极端梯度提升方法(XGBoost)和广义提升回归模型(GBM)检测英语数据集中的垃圾意见。现在一些智能优化算法开始被应用于分类问题,文献[5]提出了遗传算子和粒子群算法结合(H-FSPSOTC)来提高聚类算法性能,用于大量文本文档的分类问题。
本文利用樽海鞘群算法优化支持向量机分类器,深入研究了分类垃圾邮件的算法策略,并采用Wrapper方法[6]对函数评估,用评估指标对所提出的算法进行实验对比,能够最大程度地将垃圾邮件正确过滤。
1 樽海鞘群优化算法
樽海鞘通常以群集的方式形成相当大的鱼群进行活动,以此为灵感,Mirjalili等人[7]提出了樽海鞘群算法(Salp Swarm Algorithm,SSA),并将整个种群划分成领导者和跟随者。其中,领导者位于前端并在多维搜索空间中引导一些群体(跟随者)搜寻最佳解决方案(搜索目标)。在该算法中,整个群体位于n×d维搜索空间中,其中n是问题变量的数量,d是空间维数。种群的位置用Xi表示成二维矩阵如下:
其中i=1,2,…,n。算法的大致过程如下:
Step 1:随机初始化群体公式如下:
Xn×d=lb+rand(n,d)(ub-lb)
给定了搜索空间的搜寻范围是ub=[ub1,ub2,…,ubd]和lb=[lb1,lb2,…,lbd],来分别表示上下界。使其在搜索过程中不得超出边界,否则将它拉回到规定的范围内。这个群体在搜索空间中的搜寻目标可定义为F=[F1,F2,…,Fd]。
Step 2:更新领导者的位置公式如下:
(1)
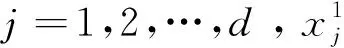
c1=2exp(-(4l/L))2
其中l是当前迭代,L是最大迭代次数。
Step3:跟随者的位置更新公式如下:
式中i≥2,表示第i个跟随者种群在第j维的位置。判断条件是否满足约束的阈值,如果是,则停止更新并输出优化结果。否则,继续迭代。
2 改进的SSA算法应用研究
2.1 改进的樽海鞘群算法
正如刘建新等人提出的混沌策略[8],本文使用改进的Tent映射,让初始种群广泛而又均匀地探索位置。初始化公式如下:
其中取μ=1/32,θ=4π时初始的种群个体分布均匀(图1)。
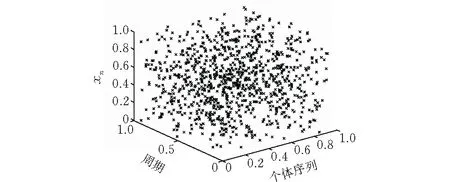
图 1 均匀分布的初始位置序列
为了提高收敛精度,将权重因子ω引入到跟随者的位置更新公式中[9],使群体在早期能够加快寻优能力,在后期搜索相对准确的结果,降低了陷入局部最优的风险。ω的非线性递减的函数公式如下:
ω(t)=ωmin+(ωmax-ωmin)×exp(-10t/T)
其中ω(t)表示第i个个体在第t次迭代时的权重取值。经多次实验取ωmin=0.5,ωmax=0.9,T是最大迭代次数。那么,新的跟随者更新公式如下:
(2)
2.2 SVM分类器
在线性SVM分类器中,决策超平面能够正确的分离训练集中的数据点,引入惩罚参数C控制了SVM的泛化能力,防止过拟合。给定训练集{(x1,y1),…,(xm,ym)},m是训练集份数,xi∈R,yi∈{-1,1},确定权向量ω和偏项b,数据点用下式进行分类。
f(xi)=sign(ωTxi+b)
其中ξi表示松弛变量。在特征空间的特征具有非线性依赖性时,将最小化函数公式(3)引入SVM,采用SVM和高斯核函数公式(4)集成。
(3)
k(xi,xj)=exp(-λ||xi-xj||2) (λ>0)
(4)
2.3 基于SVM改进算法的垃圾邮件分类
本文提出改进后的樽海鞘群算法(Improved salp swarm algorithm,ISSA)如图1所示,算法过程描述如下:
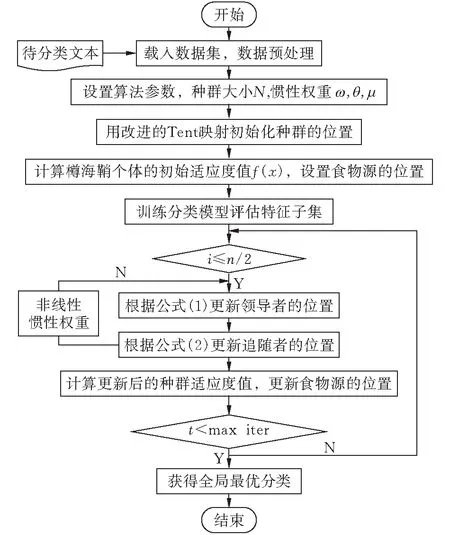
图 2 基于ISSA的垃圾邮件分类算法流程图
Step1:采用混沌映射初始化种群位置,设置参数N=80,最大迭代次数100;
Step2:对邮件的文本数据进行预处理,将文本内容分词后,创建词典作为邮件的原始特征P=[p1,w1,p2,w2,…,pn,wn],pi表示特征词,wi表示权重;
Step3:采用空间向量表示,用词频-逆向文件频率(TF-IDF)方法提取权重赋值更高的特征子集P=[p1,p2,..,pd],划分数据集;
Step4:计算个体的初始适应度值f(x),利用ISSA算法优化SVM高斯核函的惩罚参数C和λ,实验得出最佳参数;
Step5:更新个体和食物源的位置,评估分类器模型,获得全局最优分类。
3 实验与结果分析
3.1 评价指标
精确率(ACC)是正确分类的邮件与总邮件数的比例,公式如下:
其中x(i,j)表示第i个种群链在第j维的位置,N是所有个体的数量,K是种群的数量。
F-Measure(FM)是对完成分类的垃圾邮件占垃圾邮件的比例,以及对完成分类垃圾邮件占总邮件比例的整体评价,两者的值越高越有效。如
其中Nj表示樽海鞘群链的数量。
3.2 实验结果与分析
本文选取了trec06c[11]的一个公开的中文邮件数据集,其中训练集有45 360份,测试有19 440份。实验选取特征数量{500,1000,2000},惩罚因子C和λ取值范围是C={2-3,2-2,…,23},λ={2-9,27,…,23}。将ISSA与传统的SSA性能进行比较,分别采用K近邻(KNN)、逻辑回归(LR)和支持向量机(SVM)分别评估了三种不同的优化模型。
如图3、4所示,基于SVM的ISSA分类准确率和F值优于其他算法,在精确度上较其他算法也提高了0.9%~6.2%。如表1所示,基于KNN的ISSA算法的执行时间最短,然而,数据集中的合法邮件和垃圾邮件不平衡比为1.92,其他算法的稳定性不如SVM-ISSA。当迭代次数达到100时,则特征数量为2000,C=25,γ=2时,SVM-ISSA达到最佳效果,说明分类器对参数的取值较为敏感。
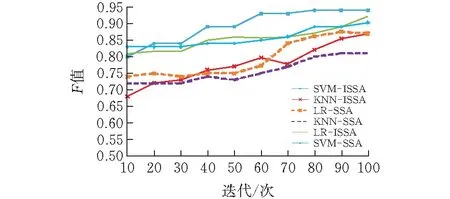
图 3 不同算法上的 F值
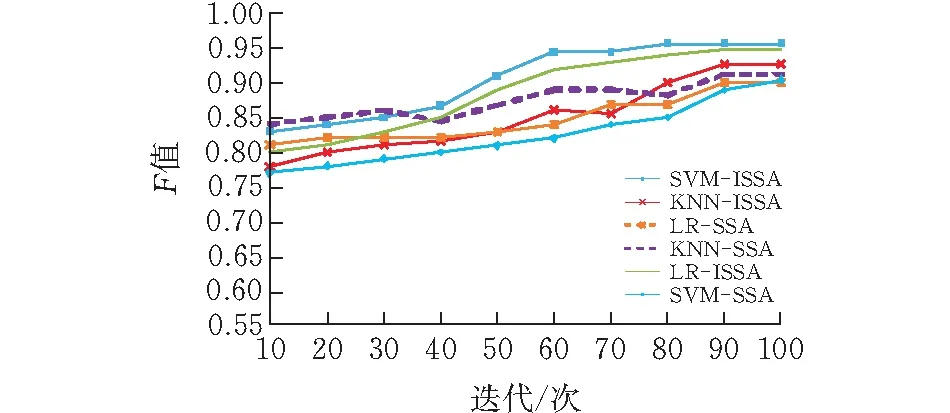
图 4 不同算法上的精确度
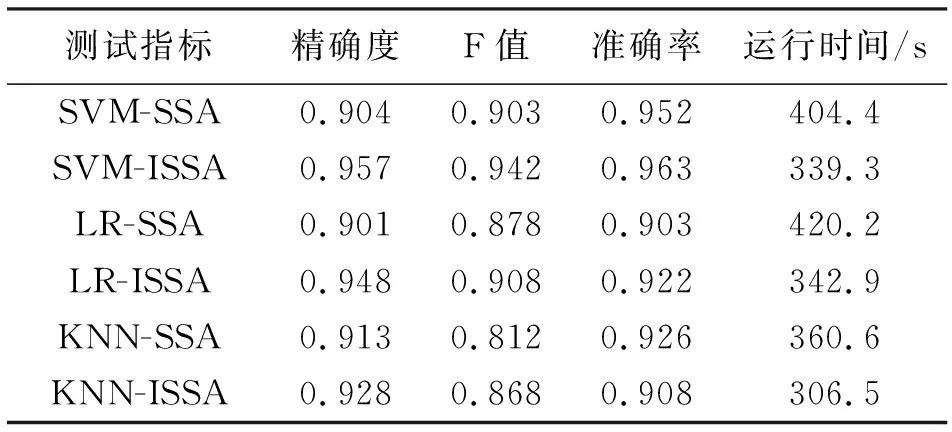
表1 实验结果
图5绘制出平均适应度函数的变化情况,与二进制樽海鞘群算法(Binary SSA,BSSA)进行对比,ISSA的收敛速度快于明显有波动的BSSA,能够快速达到均衡的状态。实验证明,ISSA在分类效果上更加稳健。
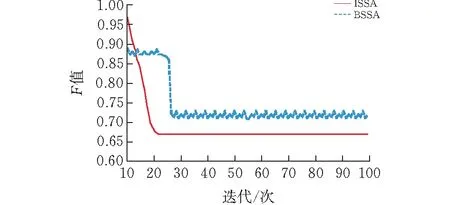
图 5 在trec06c上的适应度函数值
4 结论
将两种改进策略引入樽海鞘群算法,提高了算法的整体寻优性能,评估模型采取了三种机器学习算法用于训练分类器。其中SVM和ISSA算法模型表现出更好的性能,验证了基于樽海鞘群的SVM和ISSA分类算法在数据集上鲁棒性更好、更稳健。此外,该算法也可以用于解决大规模的工业问题。
