如何通过数学建模培养学生的创新思维
2021-02-22张娅妮李雪芳
张娅妮 李雪芳

【摘要】本文通过对高压油管的压力控制问题的分析来探讨数学建模过程中的创新思维,从而体现数学建模对创新思维的激发作用,论证了数学建模是培养学生创新思维能力的一种良好方法.
【关键词】数学建模;创新思维;高压油管;压力控制
数学建模的过程实际上是将问题数学化,并解决问题、给出答案的过程.从培养学生创造性思维的层面来看,所谓建模的思想即需要先明白问题是什么,然后理清思路解决问题;从发展学生创造能力的层面来看,它的理念、目标与现代教育的出发点和归宿,以及素质教育的内在要求是一致的.数学建模需要学生具备想象力,推理能力,综合运用各学科的知识的能力,查阅文献的能力,数学表达能力,抽象思维能力,计算、分析和处理数据能力等.数学建模既是数学课,也是劳动课和实践课.它的魅力在于“只要参与,就会有收获”,其团队作业的模式既凸显了协作的重要性,也极大地丰富和活化了创新思维.与队友交流、研讨、协作共进的过程是不断学习的过程,同时,在专业教师的启发和帮助下对方案不断地施以“重启”和“更新”是提高的过程,一刻也不能停歇的“手脑并用”的学习更是效果最佳、收获最大的学习.毫不夸张地说,参与数学建模的经历及其对学生创新思维能力的提升,将对学生整个学习生涯产生积极的影响,并使学生终身受益.
创新思维过程包括准备阶段(提出问题)、酝酿阶段(问题的求解)、豁朗阶段(问题的突破)、验证阶段(成果的证明、检验),它跟数学建模的主要步骤:问题的提出与分析、问题的假设和数据处理、建立和求解数学模型以及数学模型的评价和改进四个阶段相似,很好地说明了数学建模的过程就是对学生创新思维能力培养的过程.下面我将从解决2019年建模国赛试题“高压油管的压力控制问题”出发,来分析数学建模如何促进学生创新思维的发展.
一、问题的提出与分析,激发学生的创新思维
在这个阶段,我们为了能够解决现实问题,应做到切实地突出学生的主体学习地位,让学生作为学习的中心,同时使他们学会将数学知识进行转化.在建模中,我们要不断鼓励学生自己分析题目,发展学生自己的思维所具有的独特性和新颖性,让学生学会对已知的题目信息进行分析,抽取其中有价值的信息,同时学会对提出的问题进行归类,与所学过的数学知识联系起来,建立初步的框架,通过一步步地深入分析,不断地去激发自己的创新性思维.
以2019年建模国赛试题“高压油管的压力控制问题”为例,如果要将高压油管内的压力尽可能稳定在100 MPa左右,那么该如何设置单向阀每次开启的时长?在实际中,燃油进入和喷出高压油管是许多燃油发动机工作的基础,燃油进入和喷出的间歇性工作过程会导致高压油管内压力的变化,使得所喷出的燃油量出现偏差,从而影响发动机的工作效率.高压油管内的压强是一个持续性的变量,持续性的变量并不是十分容易研究的,所以我们需要将高压油管内的许多量离散化,这就是学生对于问题的创新性思维,即利用离散化的方法对提出的问题进行分析.题目中要研究当高压油管内的压力尽可能地稳定在 100 MPa左右时,如何设置单向阀每次开启的时长,在这里我们需要引导学生分析一下,当高压油管内的压力尽可能地稳定在 100 MPa左右时,高压油管内压强变化的决定因素是什么,同学们知道是高压油泵和喷油嘴.但实际中,高压油管内的压强一直是在波动变化的,而且我们无法详细地探究高压油管内的压强变化,所以我们在这里需要做一个状态等效,也就是当我们从高压油泵输入燃油的体积等于喷油嘴喷出的体积时,高压油管内的状态没有发生变化,也就是它依然稳定在100 MPa.状态等效这一创新点实际就是我们对题目分析之后得到的题目中暗含的意思,这样就可以去研究题目中的问题:怎么去设置单向阀每次开启的时长了.
对整个问题的分析都需要学生利用所学知识和自己的发散思维去思考,去创造出新的思维、新的解题思路,同时还要建立在符合题目要求和现实操作的基础上.数学建模不仅仅是要按照题目去解决题目,最主要的是要将实际问题与教材上的知识联系起来,在所学知识的基础上进行全新的思考和分析.
二、问题的假设和处理,创新思维的酝酿阶段
在这个阶段,学生需要根据问题进行一些适当的假设,以及对数据进行处理,也就是创新思维的酝酿阶段.这个阶段不仅要考虑问题的实际,更主要的是要运用创新思维去建立合适的模型来达到解决问题的目的,为实际应用提供更多的正确依据.愛因斯坦曾说过,“想象力比知识更重要”.虽然我们的知识是有限的,但是我们培养学生的创新能力是无限的,它是可以不断发展变化的.所以培养学生对问题的假设和处理,不仅体现了学生所学知识的基础,也体现了学生对问题的想象和创新.在问题的假设和处理阶段,我们可以让学生发挥自己的主体地位,让学生积极思考,亲自实践操作.
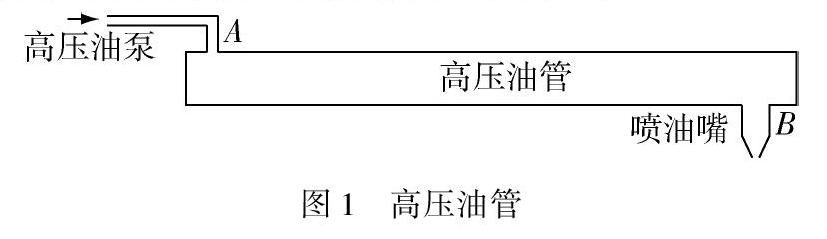
我国的高压油管工业发展迅速,高压油管应用于各个领域.由于高压油管要适应各种不同条件的要求,因此高压油管的品种繁多.燃油进入和喷出高压油管是许多燃油发动机工作的基础,因此需要控制高压油管内部的压力,防止发生事故.下面对高压油管的压力控制进行分析.某高压燃油系统的基本工作原理如图1所示,燃油经过高压油泵从A处进入高压油管,再由喷油嘴B喷出.燃油进入和喷出的间歇性工作过程会导致高压油管内压力的变化,使得所喷出的燃油量出现偏差,从而影响发动机的工作效率.
图1 高压油管
某型号高压油管的内腔长度为500 mm,内直径为10 mm,供油入口A处小孔的直径为1.4 mm,通过单向阀开关控制供油时间的长短,单向阀每打开一次后就要关闭10 ms.喷油器每秒工作10次,每次工作时喷油时间为2.4 ms,喷油器工作时从喷油嘴B处向外喷油的速率如图2所示.高压油泵在入口A处提供的压力恒为160 MPa,高压油管内的初始压力为100 MPa.
图2 喷油速率
我们要求压力尽可能稳定在100 MPa左右,那么该如何设置单向阀每次开启的时长呢?在实际中我们知道,燃油的进入和喷出导致的间歇性工作会对高压油管内产生细小的压强变化,选择最优单向阀开启时间来确保燃油的进入和喷出是最优的间歇性工作.我们可以假设忽略燃油的进入和喷出导致的间歇性工作对高压油管内产生的细小的压强变化,这样的话需要设置单向阀开启时长,使得高压油管内的压强尽可能稳定在100 MPa,然后去计算所求的问题.
这部分内容体现了学生的创新思维的假设与数据处理阶段,为接下来的模型建立与求解打下基础.在这个阶段,我们教师需要进一步提高学生的数学学习和运用能力,不断地培养学生的核心素养能力,适时地给学生一些引导,让学生能够感受到数学中的难关还是可以被攻克的,从而提高学生的建模能力和创新思维.
三、模型的建立与求解,创新思维的豁朗阶段
有了前两个阶段作为基础,我们就可以试着建立合适的数学模型,这时需要进行许多的尝试与分析,以保证最后使用的数学模型是最合适的.我们建立数学模型的目的是,能够运用数学知识将题目信息一目了然地表达出来,同时进行模型的求解,这时正是创新思维的豁朗阶段.为鼓励学生积极参与教学活动,在课堂上作为教师的我们要从知识的传授者变为知识的启发者,在学生建模的过程中,为学生起指导作用,成为学生活动的导演者和参与者,与学生平等地交流和沟通,引导学生去突破成规,大胆地提出设想和独特的见解,让学生去寻找具有创新意识的解决问题的捷径,从而达到培养学生创新思维的目的.
如“高压油管的压力控制问题”中,学生设置单向阀开启的时长,同时也要将高压油管内的压强尽可能地稳定在100 MPa.由于学生考虑到压强的变化引起的燃油体积和密度的变化的问题,因此在第二阶段假设的基础上需要建立压强变化前后的质量守恒模型,从而最终求得单向阀的工作时间.在这一过程中,学生为了解决问题,在假设的基础上建立了质量守恒模型,这是一个创新点.
这个过程是建立在之前的假设基础之上的,建立模型并进行运算,虽然不一定得出一个精确的结果,但这个结果具有很大的适用性,而且能在求解中简化运算.在实际的建模教学中,教师可以根据实际的教学内容,为学生创造生活化的教学情境,这样不仅能够降低数学知识的难度,缩短学生与数学知识之间的距离,还能够提高学生对所学数学知识的运用能力,以及学生的学习兴趣.
四、问题的评价和改进,创新思维的验证阶段
所有的创新都是对之前发现或得到的观念进行的否定或者超越,而要实现否定或者超越,就需要我们不断地进行批判.只有进行正确的批判,才会形成独特的创造力.学生要敢于发表自己的观点,养成独立思考的习惯.同时学生需要利用严格的数据来证明创新有据可依,还要保证数据计算的误差足够小.这就是为什么在建模、计算之后,要对问题进行评价和改进的原因.
“高压油管的压力控制问题”中,学生已经计算出了结果,但是他们需要去设法验证计算的误差足够小.所以学生需要查阅资料,利用所学的密度的计算公式ΔPΔρ=EP和100 MPa下的燃油密度为0.850 mg/mm3可以计算出不同压强下的燃油密度,在计算燃油密度的时候采用了递推的方法,可以减小因为ΔP导致的燃油密度的计算误差.在这一过程中学生将密度计算公式和递推法这些发散思维进行了综合运用,从而验证了计算的误差是足够小的.
在最后这个阶段,我们需要引导学生去翻阅相关的资料,了解高压油泵的具体工作原理,以及高压油泵的燃油喷出量的详细计算公式,包括如何处理持續变化中的压强,以及这个持续变化的压强对于燃油喷出的影响,同时培养学生求解的严谨性.
整个建模的过程都可以体现出学生创新思维的发展变化.数学建模竞赛从小到大,从不被熟知到广受欢迎,这是一个“培育全面发展的适应社会需要的具有核心竞争力的人才”理念在高等教育人才培养目标中凸显重要地位和顽强生命力的过程,也是大学全面培养学生创新创业能力的素质教育理念及其配套机制和措施日趋完善、成熟的过程.我们通过引导学生建立数学建模思维,培养其应用数学解决实际问题的意识和创新思维的能力.我们坚信,数学建模不再只是知识的载体,而是学生思考的创新,更多地体现了学生对思维模式的突破,潜移默化地让学生得到了锻炼,也使他们的创新思维得到了提高.
【参考文献】
[1]郑金保,缪雪龙,洪建海,等.针阀升程对小压力室喷油嘴内部空化的影响[J].内燃机学报,2014(01):52-56.
[2]姜启源,谢金星,叶俊.数学模型(第四版)[M].北京:高等教育出版社,2011.
[3]神龙工作室,殷慧文.Excel 2016办公应用从入门到精通[M].北京:人民邮电出版社,2017.
[4]左双勇.以数学建模竞赛为载体培养学生的创新思维能力[J].赤子,2017(04):130.
