一种单电感串并联电池组均衡方法

郭向伟， 刘震， 康龙云， 胡治国， 耿佳豪

(1.河南理工大学 电气工程与自动化学院，河南 焦作 454000； 2.华南理工大学 电力学院，广州 510640)

0 引 言

动力电池组内各单体不可避免的不一致性会对其能量利用率和循环寿命产生严重影响，甚至造成安全隐患[1-2]，为减小不一致性对电池组的影响，必须引入有效的均衡技术[3-4]。

通过电容、电感等储能元件实现均衡能量转移的主动均衡是近年均衡技术研究的热点。其中，基于电容储能的均衡拓扑[5-7]具有体积小，易于控制的优点，但其均衡精确度不高，若要求高精确度均衡，即要求电容电压和均衡对象电压相差不大时，往往难以达到均衡或均衡时间过长。基于电感均衡的拓扑[8-11]不受电压差的影响，具有较高的均衡精确度，但其往往需要较为复杂的开关阵列，进而导致所需控制信号较多且控制过程的可靠性降低。文献[12-14]结合电感电容储能特性提出了基于LC(inductor capacitor)谐振的均衡拓扑，采用的LC谐振电路在谐振频率附近进行开关切换，使得均衡回路中的阻抗最小，进而提高均衡效率，其对LC谐振回路切换的控制信号要求极高，且均衡对象不同，控制信号占空比也不同，导致基于LC谐振的均衡拓扑控制过程较为复杂，并且不适合包含大数量单体的电池组均衡。文献[15-19]提出的基于变压器的均衡拓扑具有均衡效率高，控制简单，且易于实现充放电均衡回路隔离的优点，但标准型号的变压器往往满足不了均衡需求，不同的电池组需要单独设计不同的变压器，导致变压器均衡拓扑的通用性较差。文献[20-22]基于Buck、Boost等变换器的均衡拓扑往往具有较为完善的均衡功能，且均衡效率较高，但其仍具有体积大、控制程序设计复杂等缺点。

文章基于电感储能均衡精度高，能量转移不受均衡对象电压差限制的特点，对基于电感的均衡拓扑展开研究，提出一种基于单电感储能的串并联电池组主动均衡方法。与文献[8-10]中基于电感的均衡拓扑相比，文献[8]中拓扑每两个单体需要配置一个电感；文献[9-10]中拓扑除了第一个单体不需要配置电感外，其余每个单体都要配置一个电感，本文拓扑只需要一个电感，大大缩小了均衡系统储能单元的体积。文献[11]中拓扑也只需要一个电感，但本文拓扑开关管数量有所减少，且均衡电流流经的开关管及二极管数量也有所减少，理论上具有更高的均衡速度及效率。总体而言，本文所提基于单电感的串并联电池组均衡方法具有拓扑结构简单、控制简单，均衡速度快、均衡效率高的特点。

1 均衡拓扑及工作原理

1.1 均衡拓扑结构

新型串并联拓扑如图1所示。各个并联的串联电池组分别标记为P1，P2…，Pm。各串联电池组中每个单体依次标记为Bx1，Bx2，…，Bxn，每个开关单元依次标记为Sx0，Sx1，…，Sx(2n+1)，x为并联电池组的序号，储能电感标记为L。二极管防止均衡过程出现短路，保证电路安全。新型串并联均衡拓扑的特点是：1)可以同时实现串并联均衡，均衡能量可以直接在任意单体间转移；2)均衡拓扑储能单元仅需一个电感，结构简单，体积小且控制简单；3)在满足器件安全的前提下，串联电池组内单体数量或并联电池组数量发生变化时，只需增减相应的开关管。

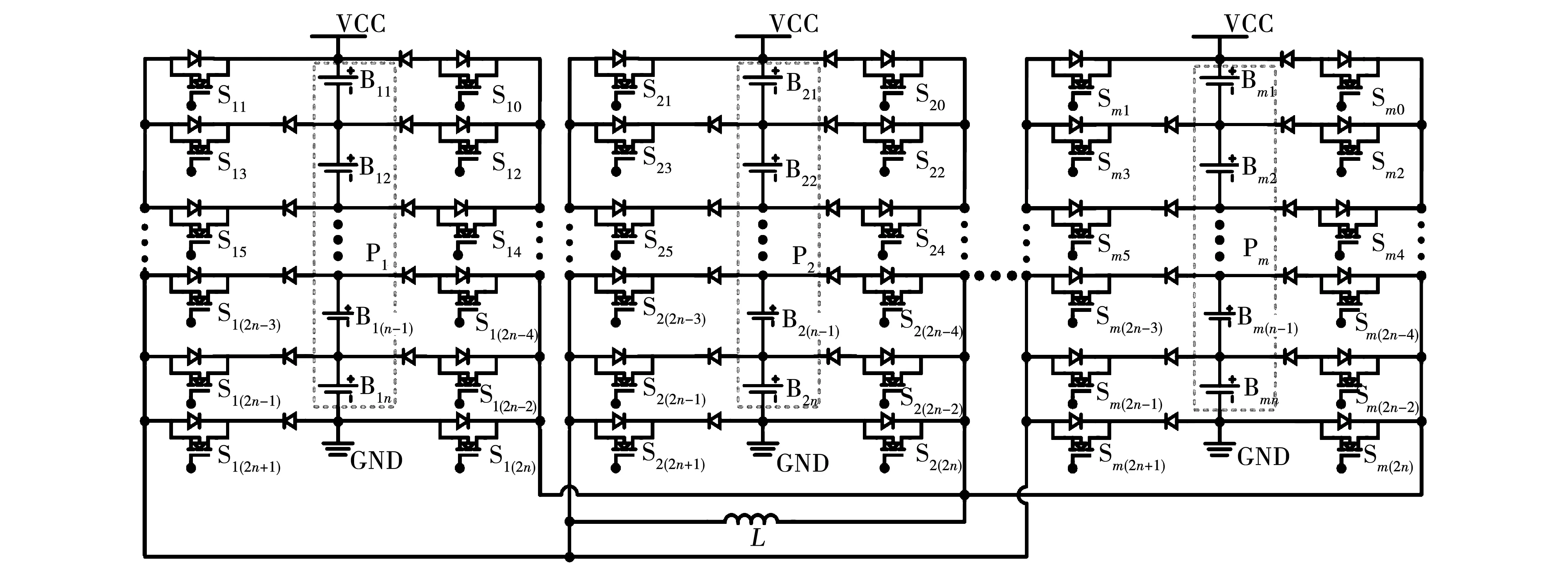
图1 新型串并联均衡拓扑Fig.1 Novel series-parallel balancing topology

1.2 均衡原理

假设串联电池组内各单体的不一致性满足均衡电路工作条件，串联电池组Px中的单体Bxi的电量最高，串联电池组Py中的单体Byj的电量最低，其中x、y为串联电池组的序号，二者可以相等；i，j为相对应串联电池组中单体的标号。一个开关周期的均衡过程可以分为两个阶段，电流回路如图2所示。

图2 新型串并联均衡拓扑均衡回路Fig.2 Balancing loop for the novel series-parallel balancing topology

第一阶段：高电量单体放电均衡，均衡路径如回路①所示。初始时刻电感L储能为零，此时控制MOS管Sx(2i-1)和Sx(2i)导通，通过回路①，单体Bxi给电感L充电，电感电流逐渐增加，当增加到设定值时，断开MOS管Sx(2i-1)和Sx(2i)，第一阶段结束。第二阶段：低电量单体充电均衡，均衡路径如回路②所示。断开MOS管Sx(2i-1)和Sx(2i)时刻，导通Sy(2j-2)和Sy(2j+1)，电感L通过回路②给单体Byj充电，电感电流下降，当电感电流降为零时，关断MOS管Sy(2j-2)和Sy(2j+1)，第二阶段结束。一个开关周期内，电感充电、放电持续的时间之和必须小于开关周期才能保证避免电感磁滞饱和。

2 参数计算

本文均衡实验采用松下公司生产的8节额定电压为3.7 V的18650型三元锂电池，选用MOS管为意法半导体IRF630，肖特基二极管为意法半导体1N5819。假设串联电池组Px中单体Bxi的电压最大且为Vi，串联电池组Py中单体Byj的电压最小且为Vj，各串联电池组电压为VP，二极管导通压降为VD，均衡周期为T，开关频率为f，电感充放电过程对应的PWM波占空比分别为α和α′。均衡第一阶段，当MOS管Sx(2i-1)和Sx(2i)导通时，单体Bxi为储能电感L充电，流过L的电流线性上升。第一阶段的时间t为αT，最大均衡电流为电感峰值电流，即

(1)

即得

(2)

一个均衡周期内，电感电流i的表达式如下：

(3)

由于一个均衡周期内，为防止电感的磁饱和，电感必须工作在电流断续模式，即能够复位，则当t=T时，t>(α+α′)T，进而

(4)

进一步推导可得占空比α的设定规则：

(5)

第二阶段开始时，MOS管Sy(2j-2)和Sy(2j+1)导通，流过电感电流近似满足斜坡函数，根据基尔霍夫定律，可得

(6)

代入上述初始条件得

(7)

将式(7)与式(1)联立，为使得一个开关周期内电感复位，则

(8)

针对均衡效率的计算，一个均衡周期，高电量单体Bxi释放的能量Wxi为电感储存的能量与均衡路径中消耗的能量之和，表示为下式：

(9)

将式(8)与式(1)和式(3)联立可得

(10)

低电量单体Byj吸收的能量Wyj为电感释放的能量和均衡路径消耗的能量之差，表示为下式：

(11)

同理可以解得

(12)

根据一个开关周期内均衡前后电池组能量的变化，可以得出此拓扑的均衡效率为

(13)

由式(13)可知，影响均衡效率的因素包含电感和开关频率的乘积，二极管的压降，MOS管占空比，和均衡对象的电压等。本节实验部分未列出具体的均衡效率值，是因为均衡效率还和均衡对象有关，而均衡对象的电压具有较强的不确定性。

另外，拓扑工作过程中，二极管和MOS管所承受的最大反向电压均近似为电池组电压，为保证电路安全工作，必须有：

(14)

其中：Vf为二极管的反向击穿电压；Vm为MOS管的击穿电压。

3 均衡控制策略

由于SOC相比于端电压更能反映单体的不一致性[23]，选取SOC作为均衡的不一致性指标。为防止电池组均衡完成后再次快速满足均衡电路启动条件，分别设定均衡启动阈值φsi和均衡停止阈值φse，其中φsi>φse。当单体差异满足均衡启动条件时，均衡控制的整体思路为：当最大SOC单体和最小SOC单体个数均为1时，对最大SOC单体放电均衡，最小SOC单体充电均衡；当最大SOC单体和最小SOC单体个数不全为1时，对序号最小的最大SOC单体放电均衡，序号最大的最小SOC单体充电均衡。每个均衡周期具体控制策略如图3所示。

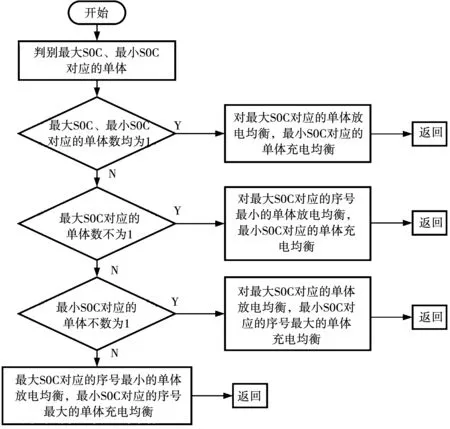
图3 串并联均衡控制流程图Fig.3 Series-parallel balancing control flow chart

4 均衡速度及效率研究

4.1 均衡速度研究

均衡速度的研究主要包含两个内容，第一个内容是将本文单电感串并联均衡拓扑和文献[11]中同样为单电感均衡的单电感双向拓扑进行均衡速度对比；第二个内容是研究单体数量变化对本文拓扑均衡速度的影响。

1)均衡速度对比研究。

进行均衡速度的分析，首先需要确定均衡速度的衡量标准，定义均衡速度为均衡前电池组单体之间最大SOC极差减去均衡后电池组单体之间最大SOC极差之后的绝对值，再除以均衡时间，具体计算公式如下：

(15)

其中Bs为均衡速度。

文献[11]中的拓扑针对串联电池组，本文拓扑同时适用于串并联电池组。为和文献[11]统一，将本文拓扑应用到串联电池组进行均衡速度的对比。在MATLAB/Simulink中搭建四单体串联电池组仿真模型。两种拓扑所有仿真参数一致，如下表1所示。以搁置状态为例进行均衡速度的对比，仿真实验结果如图4所示。根据式(15)可以分别计算出两种拓扑均衡速度分别为3.947×10-4/s和3.704×10-4/s，说明本文拓扑均衡速度高于文献[11]中的拓扑，提高了6.5%。需要说明的是换一组初始SOC值，最终均衡速度提高的比值不再是6.5%，但本文单电感拓扑相比于文献[11]的单电感拓扑，均衡速度有所提高是确定的。

表1 均衡对象仿真参数

图4 搁置状态均衡仿真曲线Fig.4 Shelved state balancing simulation curve

2)单体数量变化对均衡时间的影响。

单体数量变化对均衡时间的影响分两种情况：第一种情况是并联的电池组数量发生变化对均衡速度的影响；第二种情况是每组串联电池组中单体数量变化对均衡速度的影响。

首先研究并联的电池组数量发生变化对均衡时间的影响，仿真实验对象分别为4串1并、4串2并和4串3并电池组。每组串联电池组仿真参数与表1相同，且各个串联电池组的单体参数对应相同。同样以搁置状态为例，仿真实验结果如上图4和下图5、图6所示。3组实验的均衡时间分别为304、598和892 s，均衡速度如表2所示。由表2可知，并联电池组数量越多，均衡速度越慢，均衡速度与并联组数成反比。

图5 4串2并电池组的搁置均衡仿真曲线Fig.5 Shelved state balancing simulation curve of 4-string and 2-parallel battery pack

图6 4串3并电池组的搁置均衡仿真曲线Fig.6 Shelved state balancing simulation curve of 4-string and 3-parallel battery pack

表2 并联电池组数量变化对均衡速度的影响

其次研究串联电池组内单体数量变化对均衡时间的影响，以4单体、8单体和12单体构成的串联电池组为例分析，初始SOC最大差异设为一致，其余仿真参数参照表1，其中8单体串联电池组初始SOC分别为40%、35%、50%、38%、48%、46%、44%、42%；12单体串联电池组初始SOC分别为40%、35%、50%、38%、48%、46%、44%、42%、37%、39%、41%、43%。仿真实验结果如图4、图7、图8所示。3组实验的均衡时间分别为304、533、611 s，均衡速度如表3所示。由表3可知，串联电池组内单体数量越多，均衡速度越慢，均衡速度与串联电池组内单体数量成反比。

图7 8单体串联电池组搁置均衡仿真曲线Fig.7 Shelved state balancing simulation curve of 8 cell-string battery pack

图8 12单体串联电池组的搁置均衡仿真曲线Fig.8 Shelved state balancing simulation curve of 12 cell-string battery pack

表3 串联电池组内单体数量变化对均衡速度的影响

4.2 均衡效率的研究

均衡效率研究同样包含两个内容，首先与文献[11]中单电感拓扑进行均衡效率对比，其次研究单体数量变化对均衡效率的影响。均衡效率分析首先需要明确其获取方式，同样以搁置状态的均衡为例，计算思路为均衡后所有单体的容量之和比均衡前所有单体的容量之和，具体计算公式如下：

(16)

其中：η为均衡效率，均衡结束后所有单体容量和为Qend；均衡开始前所有单体容量和为Qinital；m为串联电池组个数；n为串联电池组内单体个数；i为单体序号。

首先进行均衡效率的对比分析，参照表1参数，对本文及文献[11]中单电感拓扑进行对比。依据式(17)求得，均衡结束后，两种拓扑效率分别为97.39%和96.79%，说明本文拓扑均衡效率高于文献[11]拓扑。其次研究单体数量变化对均衡效率的影响。先研究4串1并、4串2并和4串3并电池组的均衡效率，其仿真结果如表4所示。再研究4单体、8单体和12单体构成的串联电池组均衡效率，仿真结果如表5所示。

表4 并联电池组数量变化对均衡效率的影响

表5 串联电池组内单体数量变化对均衡效率的影响

由仿真结果可知，并联电池组个数或串联电池组内单体个数变化，对均衡效率近似无影响。

5 实验验证及分析

5.1 获取SOC

以SOC作为均衡指标，需要各单体可靠的SOC值。常见的SOC获取方法有开路电压法、安时积分法、数学模型法等[10]。其中开路电压法具有测量简单、精度高的特点，通常为其他方法提供SOC初始值，本文以开路电压法获取SOC。思路为：电池工作一段时间后，让其搁置60分钟以消除极化效应，此时读取端电压，即近似为开路电压，再利用OCV-SOC曲线获取SOC。本文实验对象如前所述松下公司生产的额定容量为3 200 mAh的18650型三元锂电池，设置SOH为1，环境温度25 ℃。电池测试系统由上位机、电子负载、示波器等组成，如图9所示。

图9 充放电实验平台Fig.9 Charging and discharging experimental platform

参照文献[10]进行曲线标定及最小二乘法多项式参数拟合，拟合结果如下：

Voc=b1×SOC6+b2×SOC5+b3×SOC4+

b4×SOC3+b5×SOC2+b6×SOC+b7。

(17)

其中：b1，b2，…，b7为多项式拟合系数；b1=3.561；b2=-14.048；b3=32.961；b4=-39.456；b5=23.766；b6=-5.694；b7=3.112。

5.2 实验结果及分析

文章设计了“4串2并”电池组进行均衡实验，实验平台如图10所示，实验参数如表6所示，串并联电池组内单体均衡过程储能电感充电和放电对应的控制信号分别为PWM1、PWM2。

图10 均衡实验平台Fig.10 Balancing experiment platform

首先对储能电感转移能量的功能性进行验证，设定单体B12需要放电，单体B23需要充电，如图11(a)所示为5个开关周期的储能电感充放电控制信号及均衡电流波形，图11(b)为5个开关周期的均衡对象电压变化波形。

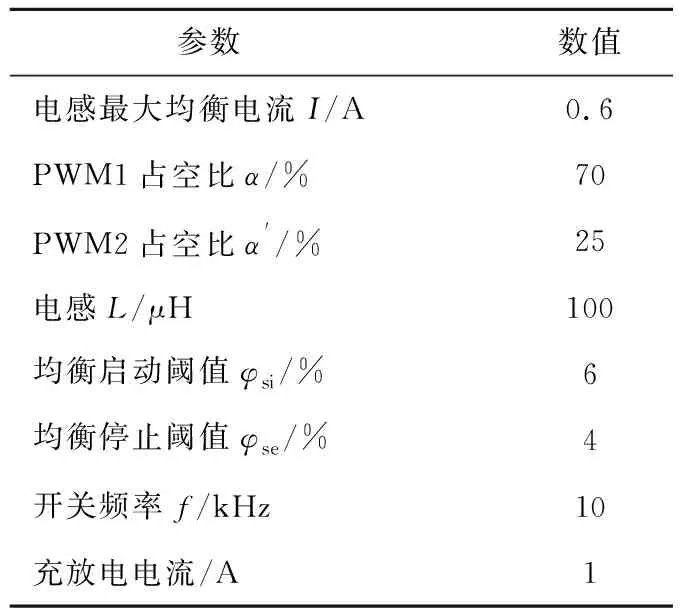
表6 均衡实验参数

由图11可知，PWM1为有效高电平时，电感电流上升，高电压单体B12电压下降；PWM2为有效高电平时，电感电流降低，低电压单体B23电压升高；整个开关过程实现了均衡能量的有效转移。两个阶段交汇处，因为电池电流发生突变，由于锂电池存在极化效应，单体B12电压升高，单体B23电压升高后又下降。

图11 均衡过程示意图Fig.11 Schematic diagram of the balancing process

其次对均衡效果进行验证，实验过程包含充电过程均衡、放电过程均衡和充放电动态均衡。动态均衡同时包含充电、放电和搁置状态。电池组充放电电流设置为1 A。首先进行充电过程均衡，电池组初始SOC极差设为11.8%，大于均衡启动阈值，均衡150 min后，各单体SOC极差下降到3.16%，满足均衡停止阈值，均衡停止；其次进行放电过程均衡，电池组初始SOC极差设为15.23%，满足均衡启动阈值，均衡120 min后，各单体SOC极差下降到3.42%，满足均衡停止阈值，均衡停止；动态均衡实验电子负载先对电池组以1A的电流充电60 min，然后以1 A的电流放电60 min，最后电子负载停止工作，电池组进行搁置状态的均衡，均衡开始时各单体最大SOC极差为26.93%，均衡240 min后，各单体SOC极差下降到2.97%，满足均衡停止阈值，均衡停止。均衡前后各单体具体SOC变化如表7所示，实验波形如图12所示。综合以上分析，本文所提基于单电感的串并联电池组均衡方法具有良好的充放电及动态均衡效果。

图12 均衡实验波形Fig.12 Balancing experimental waveforms

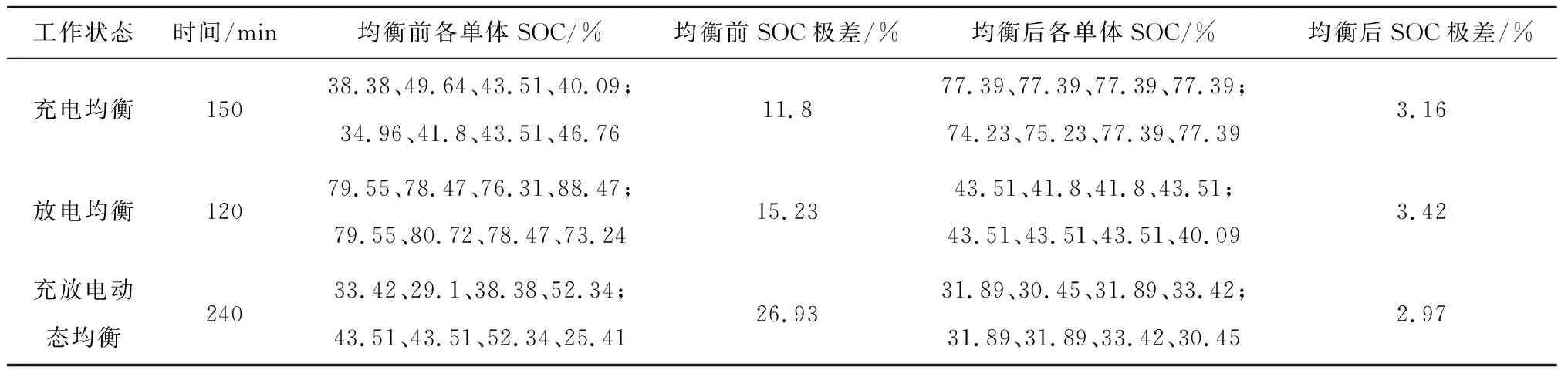
表7 均衡实验的单体SOC变化

6 结 论

文章提出一种基于单电感储能的串并联电池组均衡方法，实现SOC均衡。新型均衡方法不仅可以同时实现串并联均衡，还具有储能单元结构简单，体积小，易扩展的特点。在阐述均衡拓扑原理、参数计算及相应控制策略的基础上，通过仿真研究了新型均衡方法均衡速度及均衡效率的表现。实验结果表明，所提均衡方法可以使串并联电池组各单体SOC差异小于4%，能够显著改善电池组的一致性。本文基于单电感的新型均衡拓扑所需二极管数量较多，后期的研究集中在如何减少均衡拓扑二极管数量。