面向分布式电网的多区域协同控制方法研究

席磊， 孙梦梦， 陈宋宋， 朱继忠， 孙秋野， 刘宗静

(1.三峡大学 电气与新能源学院，湖北 宜昌 443002；2.中国电力科学研究院有限公司 需求侧多能互补优化与供需互动技术北京市重点实验室，北京 100192；3.华南理工大学 电力学院，广州 510641；4.东北大学 信息科学与工程学院，沈阳 110819)

0 引 言

提高分布式能源[1]的占有比例可以有效解决环境污染[2]和能源危机[3]问题。而高渗透率间隙性分布式能源接入电网，不仅给电网带来了强随机扰动[4]，对传统集中决策式确定性能源形成“挤出”效应，同时电网运行呈现更强的分散性、多样性和随机性特征[5]，如何有效利用分布式能源与柔性负荷参与电网调节是一个巨大挑战。

自动发电控制(automatic generation control, AGC)按照一定调节速率实时调整发电出力，以满足电力系统频率和联络线功率控制要求，是调节电网频率、有功功率和保证电网安全运行的重要技术手段，已经不能满足电网运行需求。提高AGC控制性能的有效手段之一就是探索一种能有效提高电网自适应稳定运行能力的协同控制策略。

比例-积分-微分(proportional-integral-derivative, PID)[6]是传统的AGC控制方法，利用智能算法对PID控制器的参数优化整定，比如遗传算法[7]、粒子群优化算法[8]、混合智能算法[9]。然而，随着电网复杂程度不断加剧，能量管理系统逐步走向分散，在传统AGC控制方法下，若提高部分区域的控制性能标准(control performance standard,CPS)[10]，将导致其余区域控制性能出现退化。因此，基于PID的集中式AGC控制方法难以处理这一具有随机博弈属性的分布式复杂决策问题[11]。

为此学者们将决策能力强、环境适应度高，可在与环境交互过程中反复探索与试错的分布式强化学习[12]引入到AGC。文献[13]提出利用变学习率加快调整策略的PDWoLF-PHC(λ)算法，能够加快收敛速度，应对多种分布式能源接入带来的随机扰动。文献[14]根据“后向估计”机理提出一种逼近最优值函数的渐进机制，提高AGC机组功率的调节速度。文献[15]将CPS融入强化学习指标中，实现AGC松弛控制。

上述方法虽然可以通过和环境交互修改策略，获取最优解，而“探索-利用”[15]问题仍未解决。所谓“探索-利用”即“平衡”问题，是影响智能体获取最优策略的关键因素之一。为此一些学者提出更加新颖的启发式强化学习方法，如文献[16-20]采用ε-贪婪方法，智能体基于“概率”来对“探索-利用”进行折中。文献[21-22]采用Softmax方法，智能体基于当前状态的已知平均奖励来平衡“探索-利用”，各个动作当前状态的平均奖赏越高，它们被智能体选取的概率也会相应的变大。

然而，在复杂多变的电网运行环境中，为了追求更高的控制精度，智能体需要从环境中感知更多的特征状态，以上表格型强化学习方法无法有效处理高密度信息，引发状态维数灾难。学者们研究发现深度强化学习[24]可以有效解决上述问题，如具有经验回放机制的DDQN[25]、DDQN-AD[26]、MIAC[27]。智能体在某些状态下的学习效率高于其他状态[28]，而上述方法采用均匀采样的经验回放方式，并不考虑各个样本之间的差异性。这导致学习过程中获取的经验数据没有被最大化地利用，学习效率低。用比例优先级采样[29]的优先回放方式，赋予学习效率高的状态的数据更大的采样权重，可以提高训练样本的质量，具有良好的学习效率和泛化性能。

因此，本文在具有优先回放功能的深度强化学习算法(prioritized replay double deep Q network, PRDDQN)的基础上，融入“动作空间内加权寻优”的AWM策略，形成了一种全新的多智能体深度强化学习算法，即PRDDQN-AWM(prioritized replay double deep Q network-action weighting method)，通过提高AGC系统发电指令的动态精确性能和强化学习过程中的采样效率，加快智能体的寻优速度，来获取分布式多区域协同的AGC策略最优解。通过仿真分析验证了算法的有效性，以及与其他算法相比具有更优的控制性能。

1 PRDDQN-AWM算法

1.1 DDQN

DDQN是基于神经网络的强化学习算法。采用BP(backpropagation)神经网络逼近的方法表示值函数，为了增强神经网络的稳定性，DDQN利用经验回放训练强化学习过程，智能体将数据以记忆单元(s,a,r,s′)(s为智能体当前状态，a为智能体在当前状态下采取的动作，r为智能体执行动作a后获得的奖励值，s′为智能体智能动作a后转移到的下一个状态)的形式存储到经验池中，再通过均匀随机采样的方式从经验池中抽取数据训练神经网络，从而打破数据之间的关联性。同时为了解决函数逼近时的过估计问题，DDQN将动作的选择和动作的评估用网络结构相同、网络参数不同的BP神经网络来实现，即当前网络和目标网络，分别对应两套参数θ和θ-。BP神经网络模型如图1所示，以当前状态Sn为输入，PRDDQN-AWM利用三层BP神经网络，采用tanh和ReLU作为激活函数，输入层为11维，隐含层为26维，输出层为1维。利用均方差损失函数进行参数的梯度训练。

图1 三层BP神经网络模型Fig.1 Three-layer BP neural network model

1.2 AWM

在传统强化学习中，智能体在不断与环境进行交互的过程中优化迭代Q值，进而表示当前状态下的最优动作，但是该方法需要较多试错才能获取最优动作，难以平衡“探索-利用”。在一般情况下，智能体的动作的边界值是确定的，定义动作空间为[umin,umax]，对动作边界值加权来表示当前策略的最优动作，通过调整策略w1(s)和w2(s)不断优化最优动作为

μ(s)=w1(s)umin+w2(s)umax。

(1)

为了保证每一个最优动作都只有一组策略权值相对应，使用线性计算方法对策略权值进行求解并对其归一化：

(2)

式中：ψ1、ψ2表示策略权值；f(s)表示状态s的特征向量。

为了保证智能体可以快速的逼近最优动作，并且避免陷入局部最优，采用高斯分布选择动作，将探索空间的宽度值作为标准差。在状态s下，执行动作a的概率为

(3)

式中σ表示标准差，策略的探索幅度受探索空间大小的影响，距离最优动作越近的动作被选到的概率越大。

1.3 PRDDQN-AWM

PRDDQN-AWM用优先回放取代DDQN-AWM算法中经验回放来挑选经验池N中的学习数据。经验池N中的数据由智能体的记忆单元(s,a,r,s′)组成，经验回放利用等概率原则从经验池N中抽取样本训练神经网络，但这并不是高效利用数据的方法。智能体在某些状态的学习效率高于其他状态，说明经验池存放的记忆单元对于智能体的学习并非有同等重要的意义。时间差分(temporal-difference, TD)偏差越大，表示该处智能体的学习效率越高，对应的采样概率应该越高，因此将TD偏差也存入记忆单元中。优先回放赋予学习效率高的状态的数据更大的采样概率，从而加快智能体的学习速度。

状态s下的TD偏差为

(4)

该样本处的采样概率为：

(5)

式中：pi为第i个记忆单元中的TD偏差；ε为极小的正数，避免|δ|为0；N为经验池容量。

采用优先回放的概率分布进行采样时，因为采样分布与动作值函数的分布是两个完全不同的分布，所以动作值函数的估计值是有偏估计。为了矫正这个偏差，PRDDQN-AWM融入重要性采样权重(importance-sample weights,ISW)为

(6)

式中：wi为ISW；ν为时间指数。

目标值函数为

(7)

(8)

θi+1=θi+wiα▽θiLi(θi)；

(9)

(10)

式中：θi+1为第i+1次迭代时当前网络的参数；θi+C为第i+C次迭代时当前网络的参数；θi-为第i次迭代时目标网络的参数；α表示神经网络学习率。

动作策略权值ψ1、ψ2通过最小化交叉熵损失函数进行梯度求解为

▽ψkiJ(φki)=E[-log(πψki(si+1))][r+γQθ(si+1,

πψ(si+1))-Qθ(si,ai)]▽hψki(si)。

(11)

ψki+1=ψki+β▽φkiJ(ψki)；

(12)

(13)

2 AGC系统设计

多区域协同的分布式AGC系统框架如图2所示，Δf为互联电网频率偏差，ACE(area control error)为区域控制误差。AGC系统是一个大型互联的综合系统，全面感知电网运行信息。一个区域运行状态的变化必将引起其他区域的动态变化，选取区域电网实时监测的当前环境状态量(ACE、CPS、Δf)作为AGC控制器可观测的状态，系统实时监控计算并储存互联电网每个区域的“ACE/Δf/CPS数据及长期历史记录”。区域电网PRDDQN-AWM控制器以当前系统环境的状态量为输入，计算出相应奖励值，进行在线学习，给出该区域电网调度端AGC总功率调节指令ΔPord-i。

图2 分布式AGC系统架构Fig.2 Distributed AGC system architecture

对于AGC系统的控制性能，可通过CPS进行评估和频率偏差Δf进行评估，具体如下：

1)若CPS1≥200%，且CPS2为任意值，CPS指标合格；

2)若100%≤CPS1<200%，且CPS2≥90，CPS指标合格；

3)若CPS1<100%，CPS指标不合格。

在正常稳定运行情况下，为维持系统频率稳定，频率偏差Δf必须控制在±(0.05～0.2) Hz范围内。

2.1 奖励函数

将ACE和碳排放(carbon emission, CE)作为奖励函数为

(14)

式中：ACE(i)代表ACE的瞬时值；ΔPk(i)为第k台机组的实际输出功率；η表示ACE的权值，1-η表示CE的权值，η值取0.5；n为区域机组总数；Bk是第k台机组的CE强度系数，kg/kWh；ΔPkmin和ΔPkmax分别为第k台机组容量的上限和下限。

2.2 参数设置及算法流程

为了保证学习效果，需要对6个参数γ、α、β、σ、N、ν进行合理取值，经过多次仿真，对参数进行如表1设置。

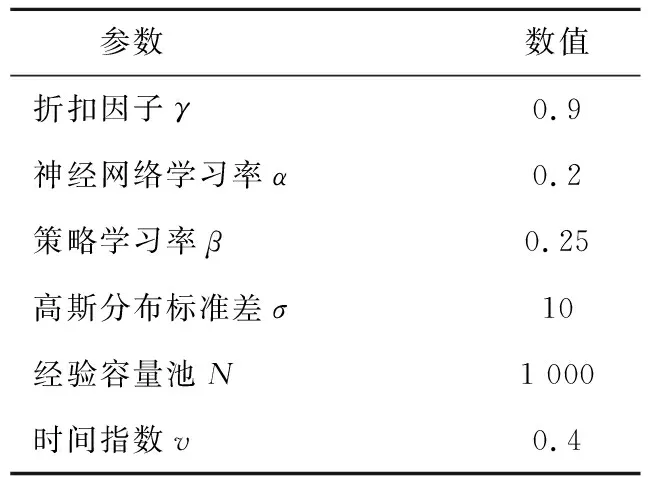
表1 参数设置

PRDDQN-AWM的算法流程如下：

Start

1：观察当前状态，根据式(2)得出w1(s)和w2(s)；

2：根据式(1)得出最优动作μ(si)；

3：根据式(3)得到策略h；

4：由策略h得到状态si下选择的动作ai；

5：执行动作ai得到新的状态si+1，根据式(14)计算出获得的奖励值ri，根据式(4)计算出时间差分|δi|，并将记忆单元(si,ai,ri,si+1,|δi|)存储在经验池N；

6：从经验池N中根据式(5)选择样本(sj,aj,rj,sj+1,|δj|)；

7：根据式(6)、(8)、(9)更新当前网络参数θ，根据式(11)、(12)更新动作权值当前网络参数ψ1、ψ2；

8：令i=i+1；

10：如果k≠k+C，返回第一步。

End

3 算例分析

搭建了改进的IEEE标准两区域负荷频率控制(load frequency control,LFC)模型[30]和广东电网模型，并对其进行仿真分析，以验证所提方法性能有效性。

3.1 改进的IEEE标准两区域LFC模型

为了模拟大规模分布式能源并网，在IEEE标准两区域LFC模型基础上改进，融入多种分布式能源，如图3所示，其参数如表2所示，ΔPtie为联络线交换功率。其中选取微型燃气轮机与小水电作为主调频机组，飞轮储能辅助调频。由于风电、光伏的随机性较强，将其模型简化，仅作为AGC系统的随机负荷扰动处理。

表2 改进两区域LFC模型参数设置

图3 改进的IEEE标准两区域LFC模型Fig.3 Improved IEEE standard two-zone load frequency control model

3.1.1 预学习

图4 PRDDQN-AWM预学习效果Fig.4 Pre-learning effect of PRDDQN-AWM

图5 6种算法的收敛结果Fig.5 Convergence results of six algorithms

3.1.2 阶跃负荷扰动

考虑到实际运行情况，对两区域引入阶跃负荷扰动，模拟电力系统中负荷突增情况，同样测试以上6种算法。A区域的控制性能如图6所示，由图6(a)可知，PRDDQN-AWM可以更快更精确地跟踪阶跃扰动。

图6 6种算法的控制效果Fig.6 Control effect of six algorithms

图6(b)显示，PRDDQN-AWM在负荷突增的情况下CPS1最小值最大。图6(c)为Δf和ACE绝对值的平均值，相较于其他算法，PRDDQN-AWM能降低|Δf|为16.42%～69.92%，减少|ACE|为15.48%～70.00%。

3.1.3 随机方波负荷扰动

在两区域模型中加入随机方波扰动，模拟电力系统中负荷不规律性的突增和突减情况。图7为各控制器的输出曲线，相较于其他算法，PRDDQN-AWM的有功功率可以精确并快速地跟踪随机扰动，可以应对电力系统负荷的不规律性突增和突减。

图7 6种算法输出曲线Fig.7 Six algorithm output curves output curve

图8(a)为控制器稳定性标准差图，计算控制器输出和负荷功率需求之间实时偏差的标准差，同时统计60次运行数据，分析可知PRDDQN-AWM标准差的波动最小，说明PRDDQN-AWM控制器具有良好的稳定性。图8(b)为|Δf|平均值，相较于其他算法，PRDDQN-AWM能降低|Δf|值62.07%～74.12%。

图8 6种算法的控制效果Fig.8 Control effect of six algorithms

图8(c)为以上6种算法在A、B两区域间的联络线交换功率偏差(Ptie)的变化曲线，其中，PRDDQN-AWM控制器的Ptie(交换功率偏差绝对值的平均值)为0.318 0 MW，最大值为1.172 8 MW；DDQN-AWM控制器的Ptie为0.565 8 MW，最大值为7.177 1 MW；Q-AWM控制器的Ptie为0.627 2 MW，最大值为7.656 2 MW；PRDDQN控制器的Ptie为2.060 28 MW，最大值为5.129 13 MW；DDQN控制器的Ptie为2.060 28 MW，最大值为5.129 13 MW；Q控制器的Ptie为3.556 2 MW，最大值为17.711 2 MW。对比可知，PRDDQN-AWM控制器的联络线交换功率偏差最小，说明A、B两区域嵌入的两个控制器获得了最优协同控制，其有功功率可以精确并快速地跟踪随机扰动。

3.2 广东电网模型

为了验证多智能体PRDDQN-AWM算法在实际电网随机环境中的应用效果，搭建了包含火电厂、水电厂、风电、光伏4种发电类型的广东电网模型，根据广东省地理分布情况，将其电网虚拟分割为粤北、粤西、珠三角、粤东4个分布式区域电网，如图9所示。

图9 广东电网模型Fig.9 Guangdong power grid model

模拟电网运行过程中出现的随机扰动，对广东电网施加随机白噪声及随机扰动。由图10为白噪声扰动下PRDDQN-AWM的控制性能，可以看出AGC功率指令可以精确地跟随负荷扰动。同时测试以上6算法在夏季随机白噪声和随机扰动下的控制性能。图11为6种算法在白噪声和随机波扰动下的CPS1指标，数据表明PRDDQN-AWM控制器的指标更优，可以获得多区域CPS1协同控制。表3可知，相较其他算法，PRDDQN-AWM能够减少|ACE|为40.037 6%～91.046 8%，减少|Δf|为30.612 2%～91.040 8%，降低CE为2.866 0%～10.176 5%。

图10 白噪声扰动下PRDDQN-AWM的控制性能Fig.10 PRDDQN-AWM control performance under white noise disturbance

图11 6种算法CPS1指标Fig.11 CPS1 indicators of six algorithms

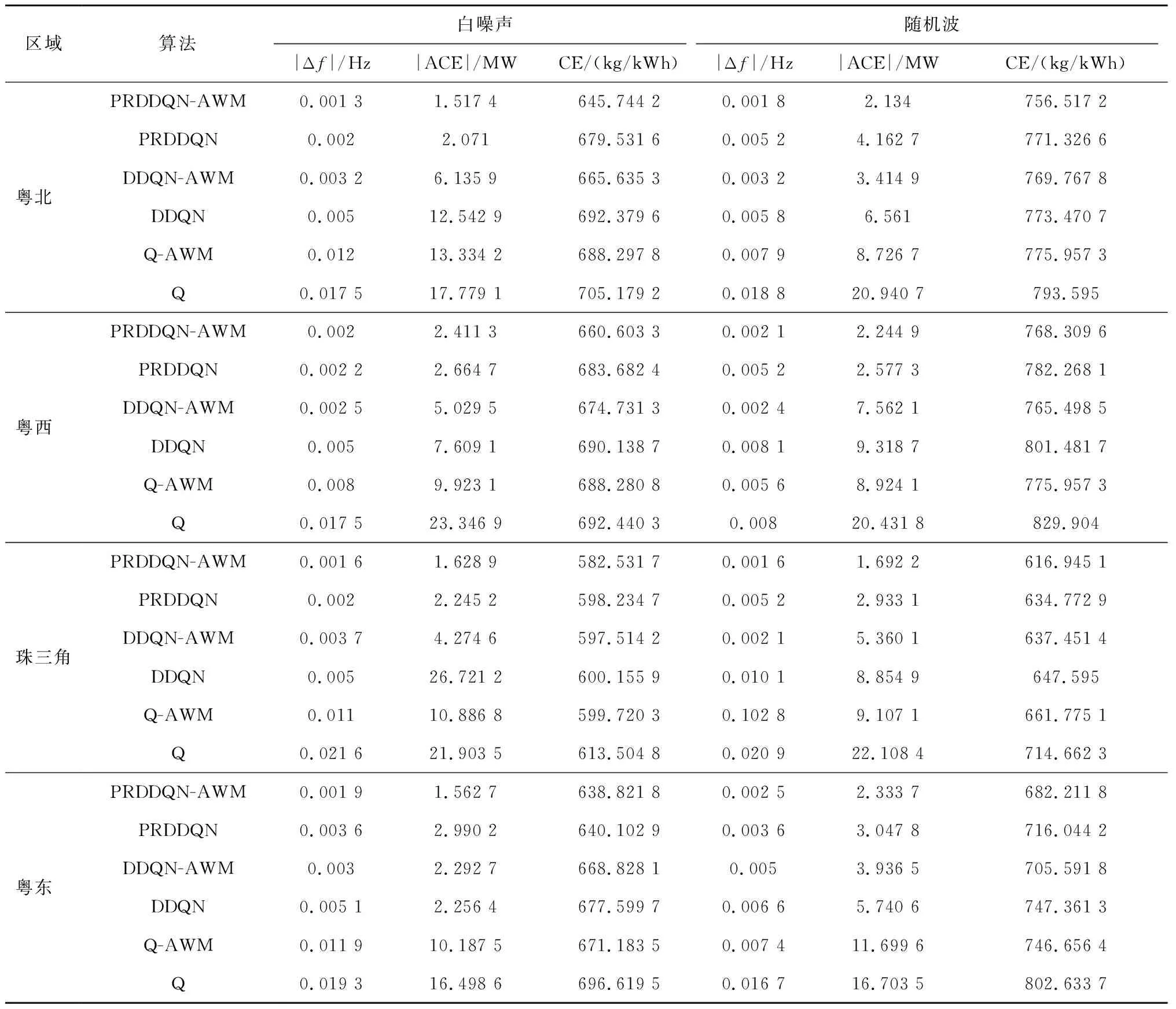
表3 白噪声扰动和随即波扰动下不同控制器广东电网仿真试验指标统计表

4 结 论

本文针对强随机环境下分布式多区域电网面临的AGC系统性能变差问题，提出了一种多智能体协同的PRDDQN-AWM算法来提高AGC性能，以获得强随机扰动环境下的多区域协同最优解。

所提方法以神经网络逼近函数为支点，采用了动作空间内加权寻优的AWM策略，避免了启发式方法在面对平衡“探索-利用”问题时，由于多次试错所带来的收敛速度慢问题；引入具有比例优先级采样功能的经验回放，提高了深度强化学习获取的稀缺经验数据的利用效率，进而提高智能体的学习能力。通过两种模型在不同环境下的大量仿真，结果显示与传统方法相比，PRDDQN-AWM可凭借其强大的函数逼近能力，提高收敛速度5.42%～93.57%，降低|Δf|为30.61%～91.04%，降低ACE为40.04%～91.05%，提高CPS为0.34～1.14%，减少碳排放2.87%～10.18%，能够获得强随机扰动环境下的多区域协同最优解。

然而，本文所采用的深度强化学习控制器仅应用于获取AGC系统的总功率指令，区域内机组的功率分配仍采用等比例分配法。因此笔者下一步的研究工作是对区域内机组功率采用智能算法进行动态优化分配，实现AGC系统整体的智能化。