经验小波变换在直流配电系统故障检测中的应用

洪翠， 连淑婷， 郭谋发， 高伟

(福州大学 电气工程与自动化学院，福州 350108)

0 引 言

直流配电网具有可提高线路输送容量，便于分布式新能源及储能设备接入，以及提高电能质量，减少线路损耗等一系列优点[1-2]，为城市配电网发展提供了新的解决方案。然而，直流配电网故障电流上升速度快，并且没有自然过零点的特性[3]，故障进入稳态后电流值会保持在较高水平，都对直流故障处置在速动性、灵敏性和选择性方面提出了较高的要求，快速可靠的故障检测更是意义重大。

近年，已有许多直流故障检测研究。文献[4-5]分析直流配电网故障检测、故障定位与隔离的过程，指出故障检测是保护关键问题之一。文献[6]提出名为“握手法”的故障线路识别方法，简单易行，只是识别速度难以达到速动性要求，且非故障线路会短时停电。文献[7]结合“握手法”提出基于直流断路器的故障检测方法，但对供电可靠性影响较大。文献[8]利用线路两端通信设备所接收的过电流信号检测故障，识别速度有所提高，但存在通信同步性的问题。文献[9]提出一种依托限流电感电压变化率的故障检测方法，但相邻线路故障对此方法造成的影响未分析。文献[10]利用小波变换提取高频暂态分量检测故障，但易受噪声影响。文献[11]提出以智能算法提取特征的故障检测方案，但训练具有一定局限性，是否适用于其他结构的配电网有待研究。

本文提出基于经验小波变换(empirical wavelet transform，EWT)的直流配电系统故障检测方案，该方案首先利用EWT分解故障电流信号获得模态分量f2，进而通过希尔伯特变换辨识f2的瞬时幅值，据此构造出检测判据而实现直流故障的快速检测；为更便利于后期故障处置措施应用，本文借助于自动编码器(auto-encoder，AE)和支持向量机(support vector machine，SVM)实现了直流线路故障类型识别；并通过在PSCAD/EMTDC仿真平台上所搭建的直流配电系统模型，仿真验证了所提出检测方案的可行性与快速有效性。

1 直流配电线路故障

直流配电线路常见故障有极间短路、单极接地故障。其中，单极接地故障多因外力损坏、绝缘层老化等导致，虽然造成危害较小，但其发生概率更高。以图1所示“握手式”柔性直流配电系统[5]为例分析直流配电线路故障。当T2端口侧线路5正极接地故障时，等效电路如图2所示。

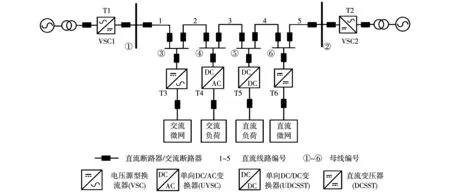
图1 柔性直流配电网Fig.1 Structure of a flexible DC distribution network

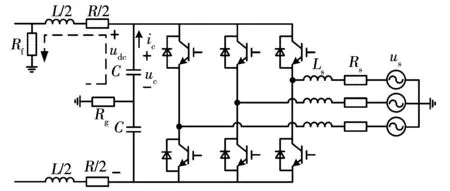
图2 单极接地故障等效电路Fig.2 Equivalent circuit of the pole-to-earth fault

图2中：us为交流侧等效电源；Rs和Ls为交流侧等效电阻和电感；C为直流侧正、负极电容值；Rg为电容接地电阻；R/2是直流线路等效电阻；L/2是直流线路等效电感；Rf为故障点过渡电阻；ic为电容放电电流；uc为正极电容电压。

单极接地故障可分为直流电容放电和二极管自然换相两个阶段[4]。直流电容放电阶段，故障极电容所存储电荷通过故障极线路、短路点过渡电阻及接地点所构成回路放电，放电回路如图2中虚线标识。电容放电阶段中直流电压udc始终大于交流侧线电压，续流二极管承受反向电压处于关断状态，此时的故障电流主要由故障极电容放电电流组成。当直流电压udc与交流侧线电压数值相当时，换流器二极管开始换相导通，交流侧通过二极管向故障点馈入电流。电容放电阶段的暂态过程可表示为

(1)

短路点过渡电阻Rf较小时，故障回路处于欠阻尼状态，正极电容电压振荡衰减至零；短路点过渡电阻Rf较大时，故障回路处于临界阻尼或过阻尼状态，电容将以非振荡形式放电，正极电容电压单调地趋于零点。最终，正极电压接近于零，负极电压在定直流侧电压的控制作用下变为原来的两倍。故障发生后正极电容放电，线路电流出现振荡现象，之后逐渐恢复正常。振幅和故障点过渡电阻有关，过渡电阻越小，振荡幅度越大，且持续时间越长。

图1网络中，T2端口侧换流器VSC2出口处正极接地故障时的仿真波形如图3所示，可以看出，仿真结果与上述理论分析相符。此外，高值过渡电阻接地故障情况下，故障电流上升缓慢，进入稳态后的幅值也比较低，波形与正常的负荷变动类似，基于电流幅值进行故障检测时，可能产生漏检、误检。在低值过渡电阻接地情况下，故障电流幅值大，且故障电流上升速度较快，若无快速有效的特征提取方法，将难以及时检出故障并采取后期隔离措施，可能危害整个直流系统稳定性。

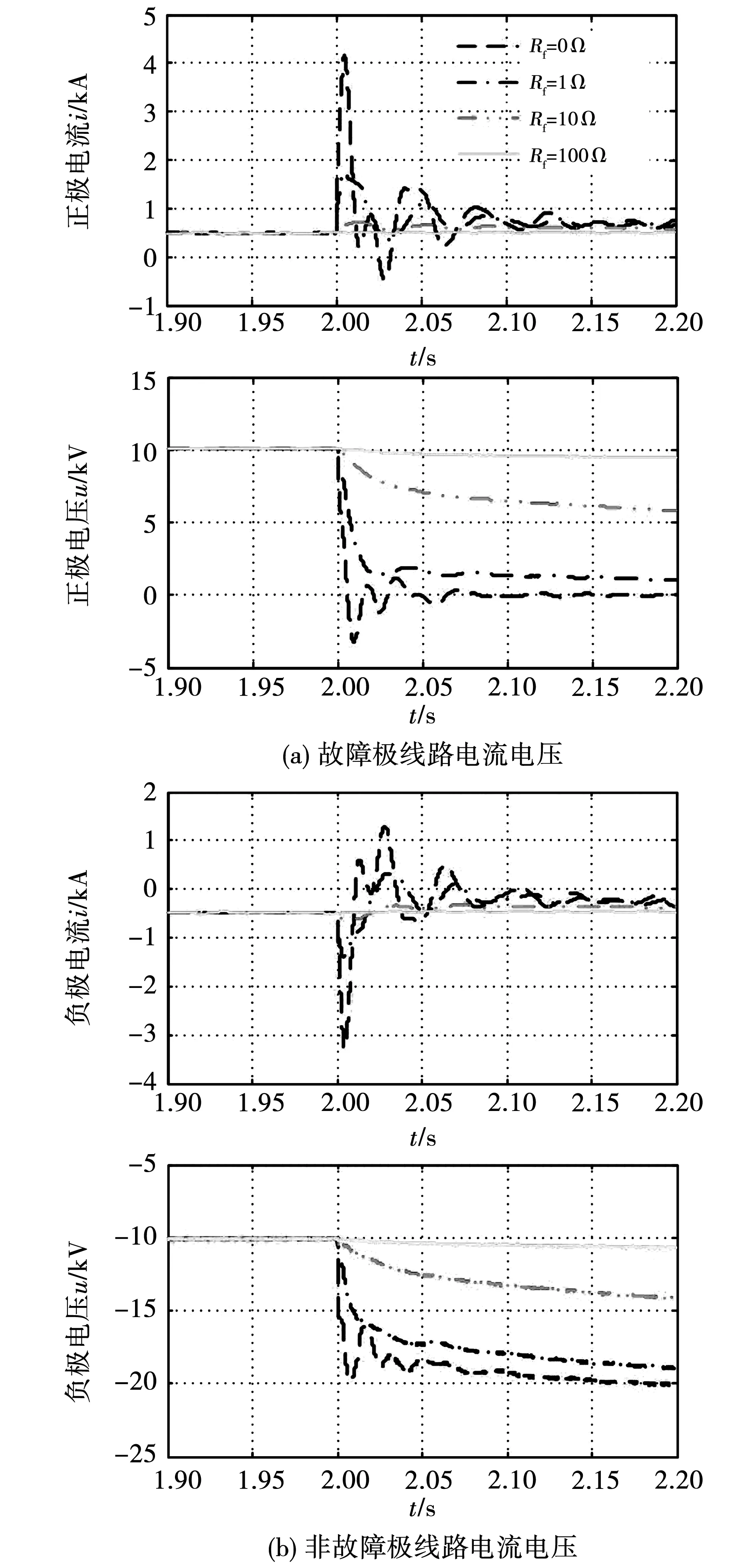
图3 正极接地故障仿真结果Fig.3 Results of the positive grounding fault simulation

2 故障检测特征提取

2.1 经验小波变换(EWT)

Gilles结合经验模态分解(empirical mode decomposition，EMD)的自适应理论及小波变换(wavelet transform，WT)的理论框架，提出一种称为经验小波变换(EWT)的信号处理方法[12]。EWT根据傅里叶频谱特性自适应地选取一组小波滤波器来提取信号的调幅-调频(AM-FM)分量，可以克服EMD由于收敛条件不合理出现的模态混叠及理论依据不充分的问题，已在心电信号处理领域获得了较为广泛的应用[13]，并且EWT在分解计算时间上小于EMD分解。因此，本文考虑将EWT应用在直流配电网的直流侧线路故障检测领域。

EWT算法实现步骤如下：

1)自适应分割傅里叶轴。

分割过程如图4所示，为符合香农采样定律，将傅里叶轴的划分区域限制在[0，π]，在[0，π]上划分N个区域，每个区域可以表示为Λn=[ωn-1,ωn]，以边界ωn为中点，定义图中阴影部分2τn为过渡段。划分傅里叶轴的关键是找出N+1个边界点的位置，其中0、π是固定的边界点，再通过寻找频率范围内的局部极大值可给出另外的N-1个点[12]。

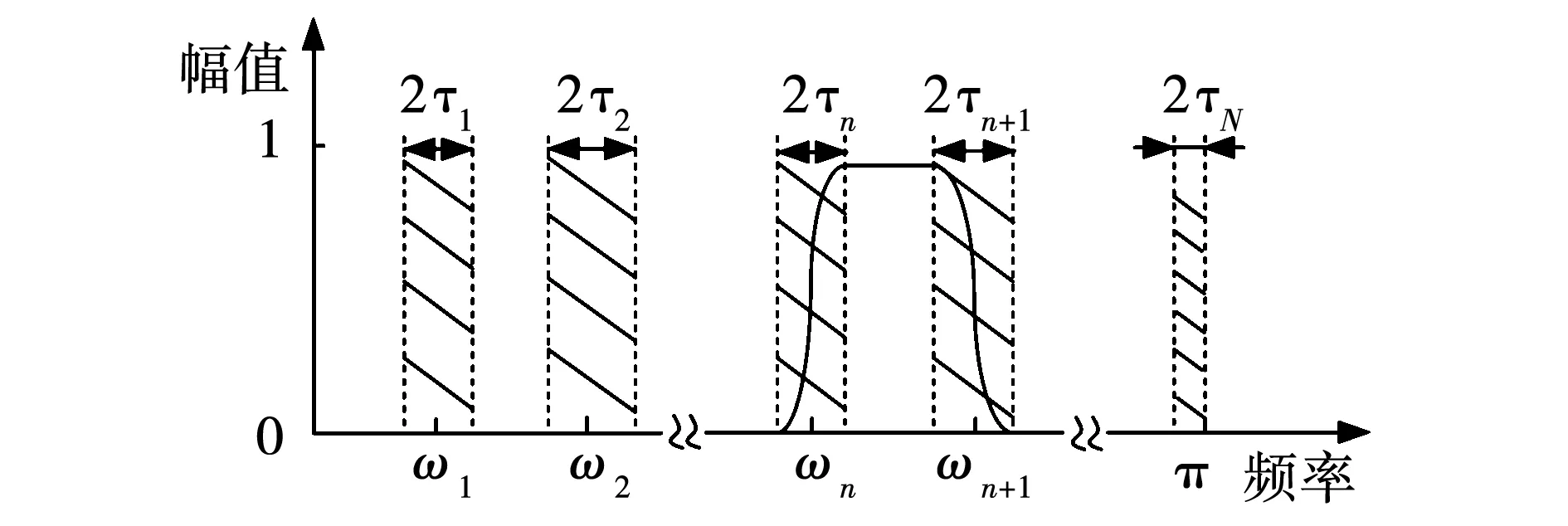
图4 傅里叶轴的分割Fig.4 Partitioning of the Fourier axis

2)定义经验小波。

经验小波定义为每个区间Λn上的带通滤波器，其构造方法借鉴Meyer小波，经验小波函数和经验尺度函数分别定义为：

(2)

(3)

式中：

β(x)=x4(35-84x+70x2-20x3)。

(4)

(5)

3)定义小波系数。

利用传统小波的方式定义经验小波细节系数：

(6)

近似系数：

(7)

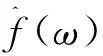
信号可以重构为：

(8)

式中“*”表示卷积。

重构信号的经验模态分量为：

(9)

2.2 基于EWT的故障特征提取

图1网络T2端口换流器VSC2出口处正极金属性接地故障时，故障电流的EWT分解模态分量f0～2如图5所示，该电流EMD分解结果如图6所示。

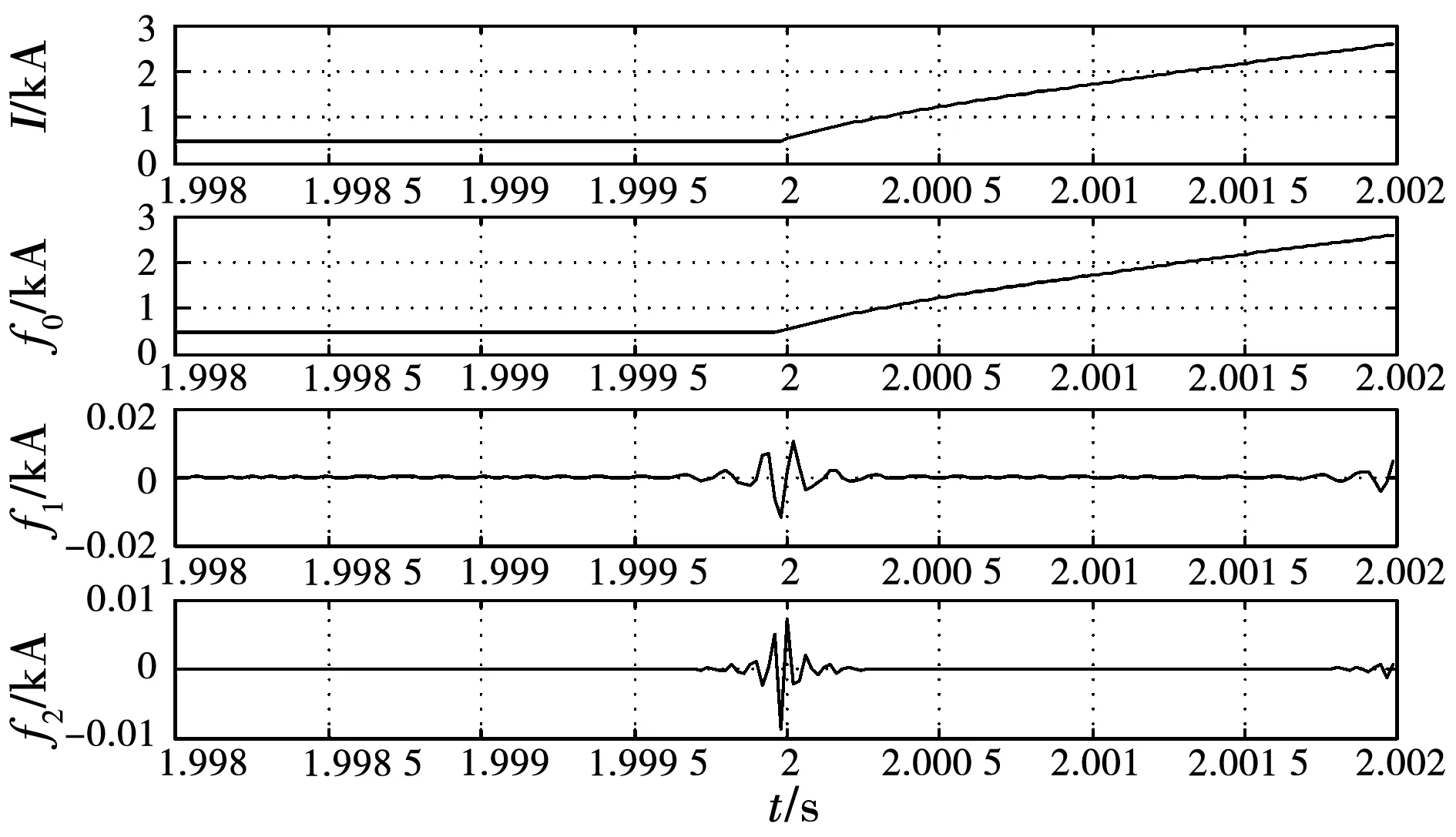
图5 故障线路电流信号的EWT分解结果Fig.5 EWT decomposition of the fault current

可见，EWT分解可准确提取并表征出故障分量，且时域局部化程度好，这主要得益于Meyer小波良好的频域光滑特性，即时域衰减够快。同一电流信号应用EMD方法，则由于终止条件不够合理导致信号分解不完全，仅分解出2个IMF模态分量，且分解出的IMF1、IMF2模态分量突变特征不突出，从物理意义方面也难以对原信号进行解释。另外，为获得IMFn模态分量，EMD需进行多次迭代，相比EWT计算量较大，消耗时间较长。因此，在处理非线性非平稳信号方面，EWT变换明显优于EMD变换。不过，EWT分解得到的模态分量末端存在边界效应[14]，实用中可通过边界拓延再截取的方式减小边界误差。

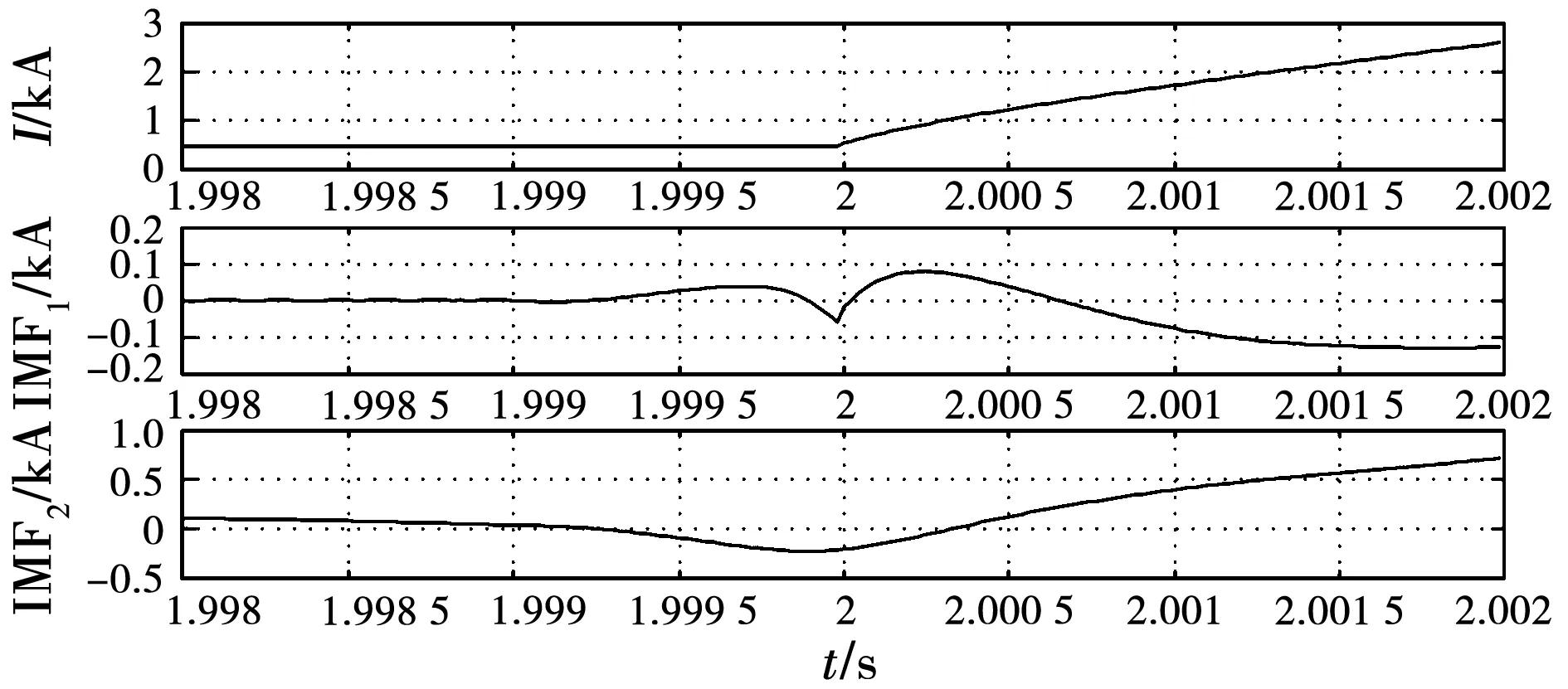
图6 故障线路电流信号的EMD分解结果Fig.6 EMD decomposition of the fault current

实际上EWT后半部分和小波分解类似，则f0和fn可以理解为故障电流的低频段和高频段信号。通常高频分量能够较好地表征故障电流突变的特点，因此，本文选择f2作为故障电流的特征，并据此开展下一步的分析。假设图1网络T2端口侧在换流器VSC2出口发生过渡电阻为100 Ω的正极接地故障，其线路电流EWT分解得到的f2如图7(b)所示。由于负荷投切和高阻故障的电流信号有一定的相似之处，为了对比分析，负荷投切电流EWT分解结果f2如图7(a)所示。

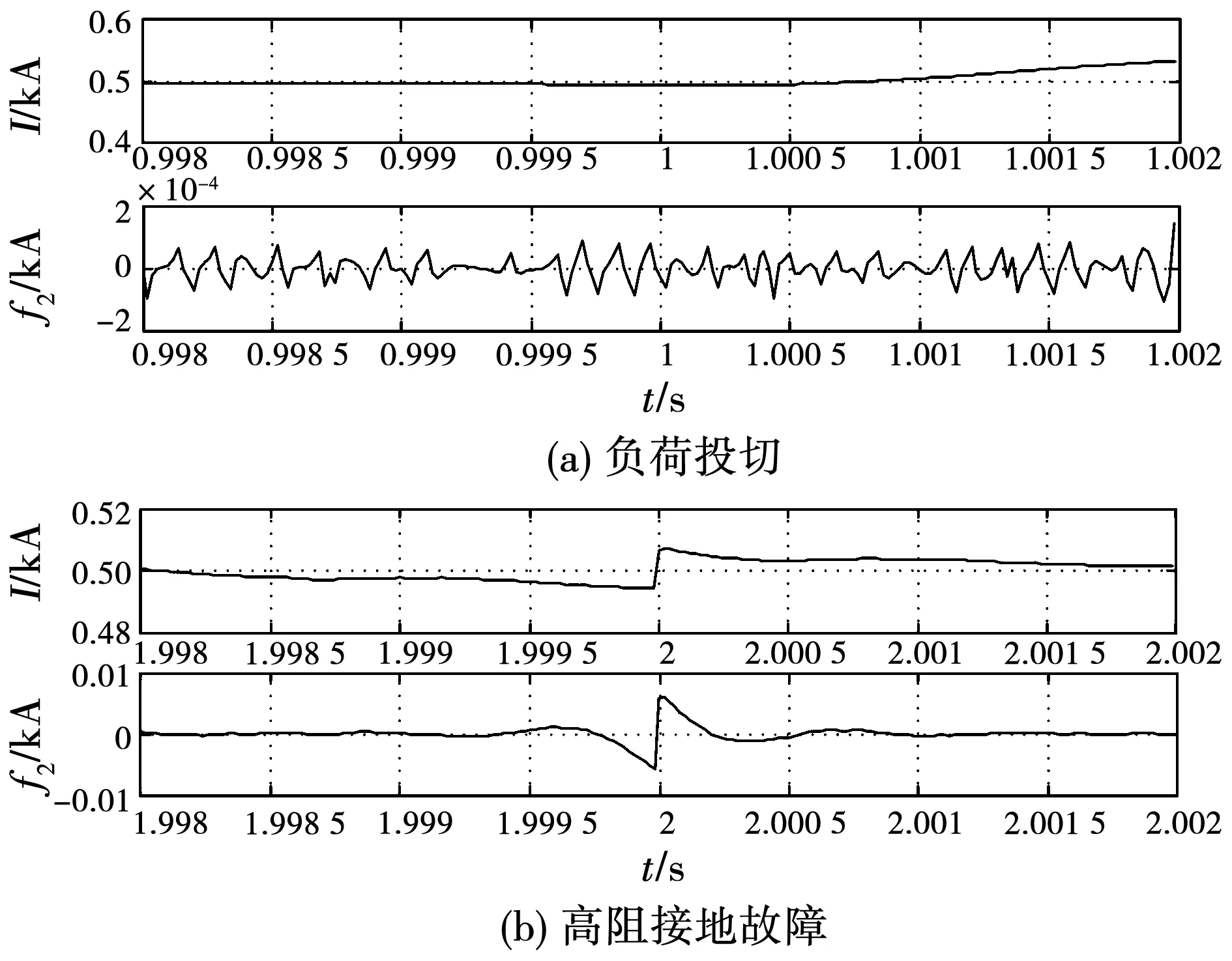
图7 不同工况下EWT分解得到的f2Fig.7 f2 of EWT decomposition under different working conditions

由图7可以看出，在较高阻值情况下，故障电流EWT分解出来的高频分量f2仍然突变明显，准确表征了故障，而对于负荷投切工况，f2没有明显的突变点，幅值变化和高阻故障也不处在同一个数量级上。可见，f2能够准确表征故障的特征信息，这为下一步构造准确的判据奠定了基础。

3 故障检测与辨识

3.1 检测判据的构建

为准确辨识出EWT分解得到的分量f2的幅值信息，并据此构造出检测判据，对f2利用希尔伯特变换(Hilbert transform，HT)进行参数辨识。若x(t)表示原始输入信号，H[x(t)]表示经过希尔伯特变换后的输出信号，希尔伯特变换的时域表达式为

(10)

利用原始输入信号x(t)和经过希尔伯特变换的输出信号H[x(t)]就可以构造一个新的复函数X(t)，其实部为原始信号，虚部为经过希尔伯特变换后的信号，这个复函数也被称为解析信号：

A(t)eiθ(t)。

(11)

式中：

(12)

解析信号的幅值A(t)可以被视为原始信号的瞬时幅值，对解析信号的相位角θ(t)求导后再除以2π可得原始信号的瞬时频率。

对图7所示分解结果进行参数辨识，得到解析信号的幅值结果如图8所示。

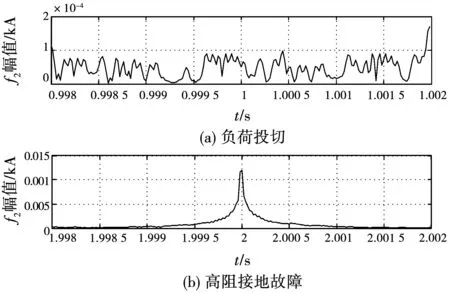
图8 不同工况下希尔伯特变换辨识f2的幅值Fig.8 Identification of f2 amplitude by Hilbert transform under different working conditions

本文设计的故障检测过程为：首先对电流信号按照2.1节进行EWT分解，之后选择f2分量作为故障特征量，而后运用希尔伯特变换辨识f2得到幅值，求得该分量的幅值最大值f2_Amp，并设定阈值δ，当满足式(13)时，即判定为发生故障。

f2_Amp>δ。

(13)

式中，阈值δ设定按照躲过负荷投切工况下f2的幅值最大值考虑。

3.2 故障分类

为方便后续保护动作，还需在检测出故障的基础上对故障类型进行判断。因此，判定发生故障之后，进一步考虑将EWT分解故障电流信号得到的分量f0～2以及正极电压up输入到自动编码器提取故障特征。

作为一种无监督学习的神经网络模型，AE能够找到最能区分数据的特征，该模型可分为编码网络和解码网络[17]，原理结构如图9所示。

图9 自动编码器(AE)结构Fig.9 Structure of the AE

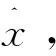
自动编码器的编码过程如下：

h=f(Wx+b)。

(14)

解码过程如下：

(15)

定义损失函数为

(16)

其中：W、W′为权值；b、d为偏置；f、g分别为编码网络和解码网络的激活函数；m为样本总数；θ为所有的参数集合。

本文采用4层AE结构对原始数据进行特征提取，并根据上述的方式进行参数回归，最终得到降维后的特征量h。输入的原始数据，除了EWT分解故障电流信号得到的前3个模态分量f0～2以外，还增加了正极电压up，该电压即为图2中正极电容电压uc。当极间短路故障时，up下降至零，下降速率与过渡电阻有关；负极接地故障时，up变为原来的两倍，且故障瞬间up有上升的趋势；正极接地故障时，up下降为接近零的数值，且故障瞬间有下降的趋势。up的加入将有助于自动编码器更好地提取故障特征，提高分类准确率。在提取出特征量h之后，以SVM实现故障类型的划分。

受检测系统周边电磁环境的影响，可能存在高频信号混入故障检测信号的情形。本文考虑采用典型的小波阈值去噪方法[19]去除电流信号噪声，从而提高抗环境高频信号干扰能力。其中，采用的小波系为Sym2，分解层数为5层。因此，基于本文提出检测方法的故障检测辨识流程如图10所示。

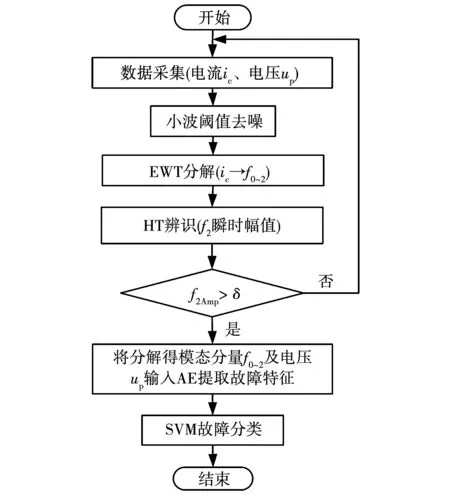
图10 故障检测流程Fig.10 Flowchart of the fault detection

4 仿真验证

在PSCAD/EMTDC仿真平台搭建图1所示握手式柔性直流配电系统的仿真模型。其中的两个VSC换流站，一端采用定直流电压控制模式，另一端采用定有功功率控制模式；接入负载包括直流负荷、交流负荷、直流微网以及交流微网的四类；直流侧采用电容中性点经电阻接地方式，阻值设为9.9 Ω；直流线路采用RL等效模型，主要的仿真参数见表1。

表1 仿真模型参数

4.1 检测算法的仿真验证

依照如图10所示的工作流程验证故障检测算法，采样频率为50 kHz，窗口数据100点，综合考虑并设定f2的瞬时幅值阈值δ为5.74e-4。以换流器VSC2出口处直流线路发生正极金属性接地故障为例，故障检测的仿真结果如图11所示；同点经过渡电阻接地时的故障检测仿真结果如图12所示。

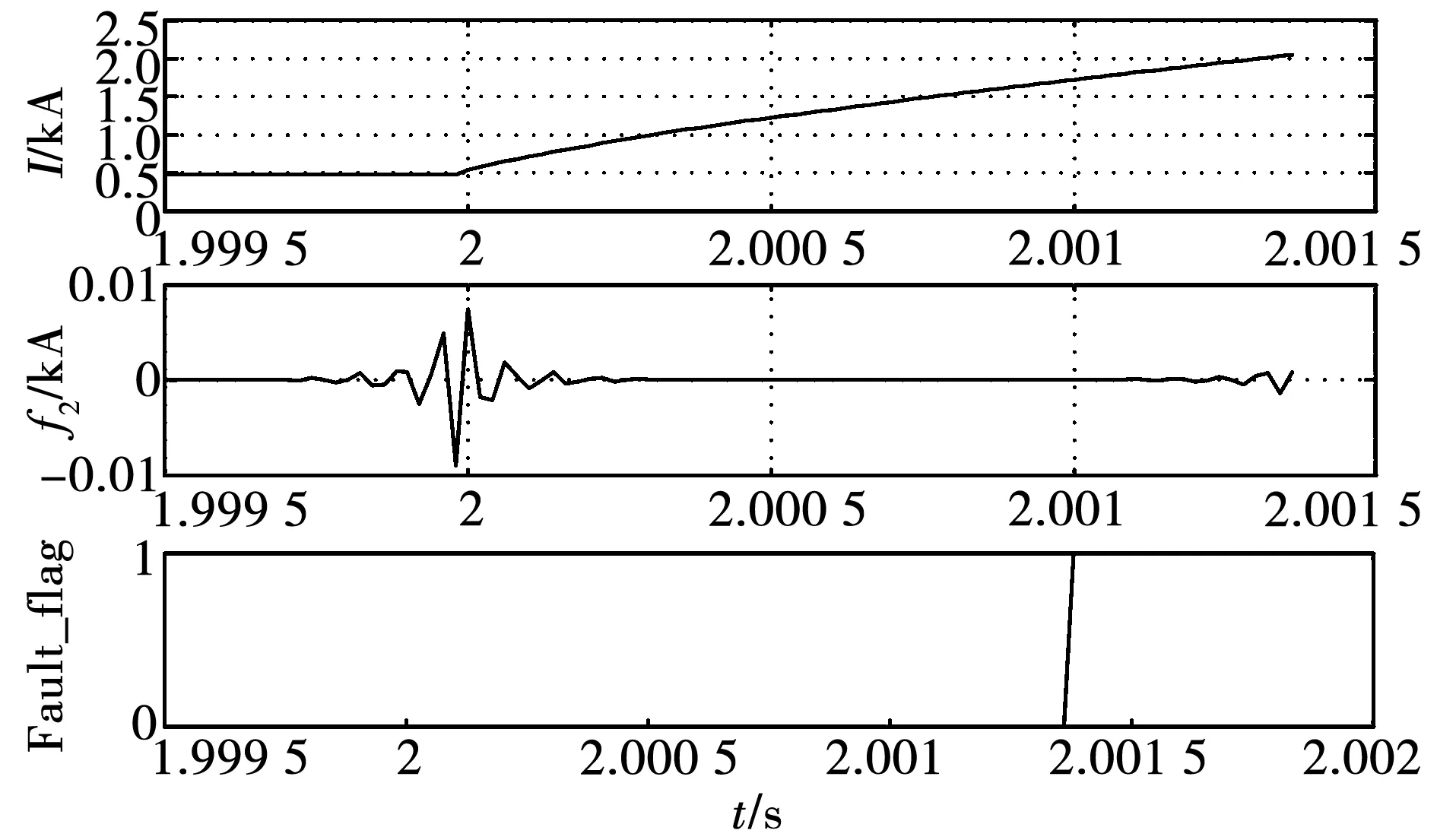
图11 正极金属性接地故障仿真结果Fig.11 Simulation results of positive metal grounding fault

由图11、图12的仿真结果可知，运用EWT分解故障电流得到模态分量f2，并以f2的瞬时幅值最大值作为故障判据，能满足检测技术的快速需求，且由于算法本身的快速性，即便有延迟，仍然能够在故障电流上升至最高点之前检测到故障，并不影响快速开展故障后期处置。

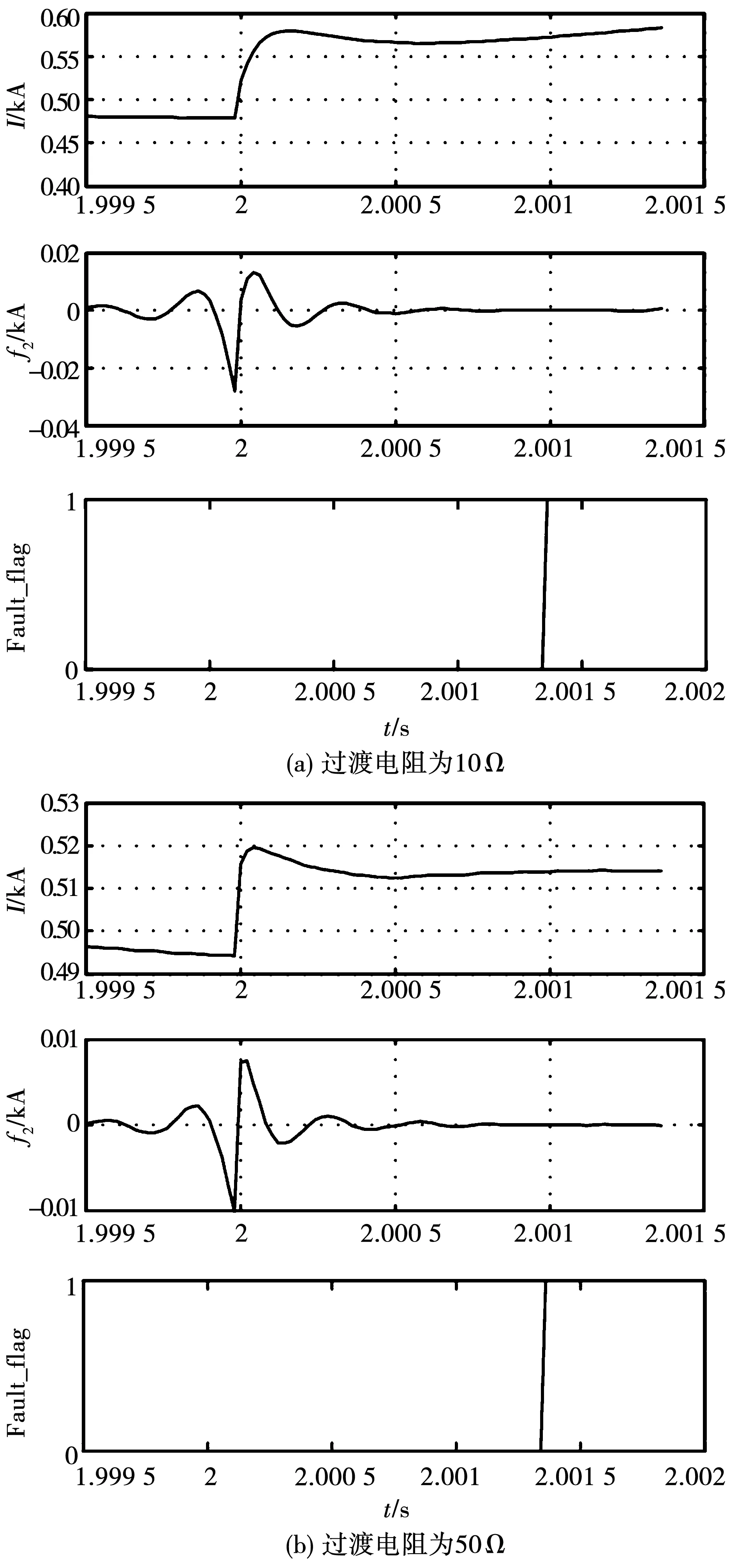
图12 正极非金属性接地故障仿真结果Fig.12 Simulation results of positive non-metallic grounding fault

4.2 场景不同时的故障检测

当直流配电系统中的直流线路发生极间短路及正极接地故障时，表2给出不同故障场景下对故障的检测结果，其中近端故障距离出口0 km，远端故障距离出口7 km，过渡电阻变化范围为0～100 Ω。

由表2的故障检测仿真结果可得，不论是极间短路还是单极接地故障，随着距离的增加，f2幅值均有所降低，这是因为线路电感会对高频分量产生较大的衰减。单极接地故障过渡电阻越大，故障电流幅值越小，那么相应分解出来的分量幅值也会减小。但即便在线路远端发生正极接地故障，且过渡电阻高达100 Ω，该高频分量幅值仍然大于设定的阈值δ=5.74e-4。此外，由于电阻对高频分量的衰减影响比较小，因此，本文设计的检测方案具备较强的短路点过渡电阻耐受能力。

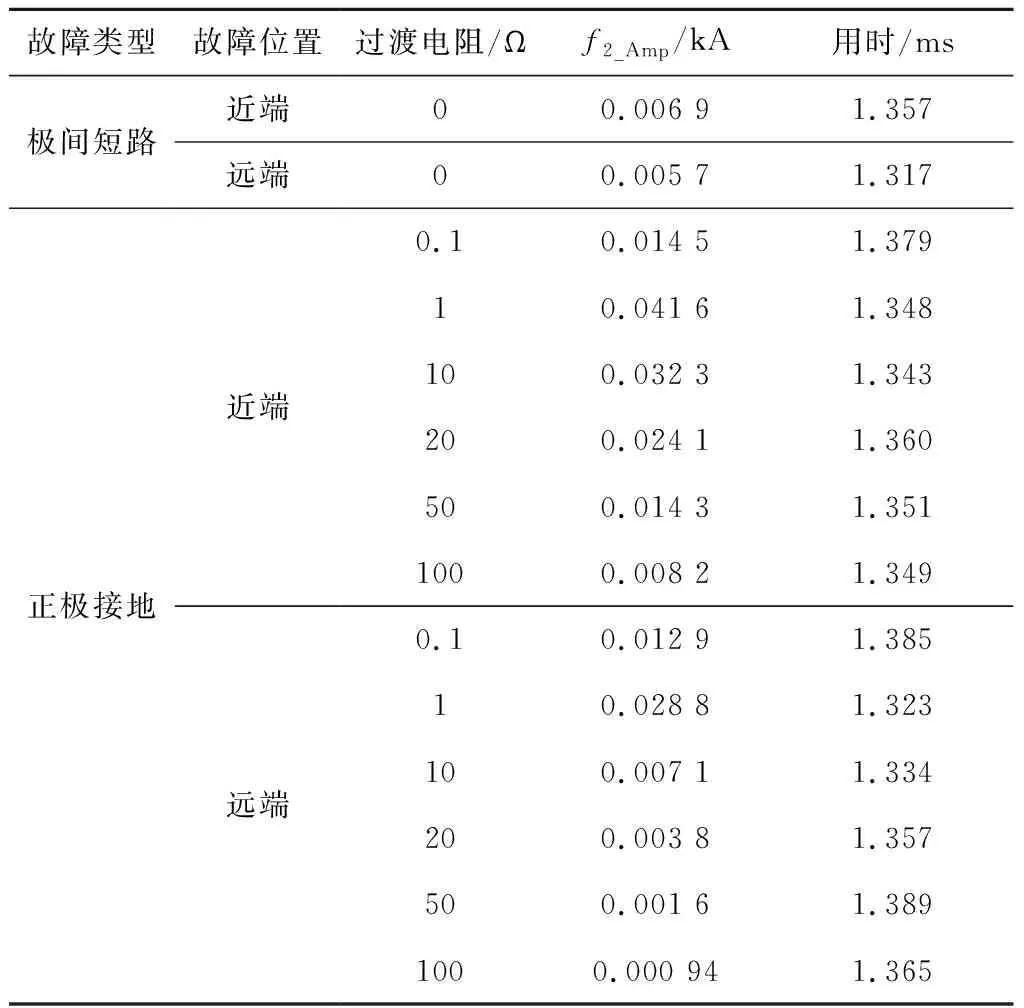
表2 不同场景的故障检测结果

4.3 电流变化率的影响

直流配电系统发生金属性接地、经过渡电阻接地故障时，可能由于阻抗的差异导致电流上升速率不同，进一步影响电流信号中的高频分量。仿真不同电流变化率时EWT分解电流得到的高频模态分量f2及故障检测结果如图13所示。

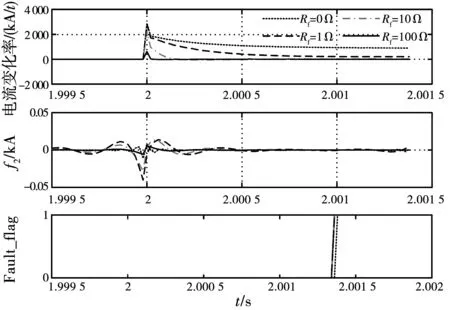
图13 电流变化率及高频模态分量Fig.13 Current rate of change and high frequency modal components

由图13可知，直流配电线路发生经过渡电阻接地故障时，过渡电阻越小，电流变化率越大，高频模态分量f2幅值越高，波动程度大。发生金属性接地故障时，电流变化率最大，f2幅值却小得多，波动程度小，原因为EWT可自适应划分傅里叶轴，如图14所示，f2包含的频带不一致，使金属性接地故障与非金属性故障电流信号采用EWT分解得到的高频模态分量f2在波动程度、幅值等方面存在差异。但不论电流变化率大小，本文所提方法都能正确检测出故障。

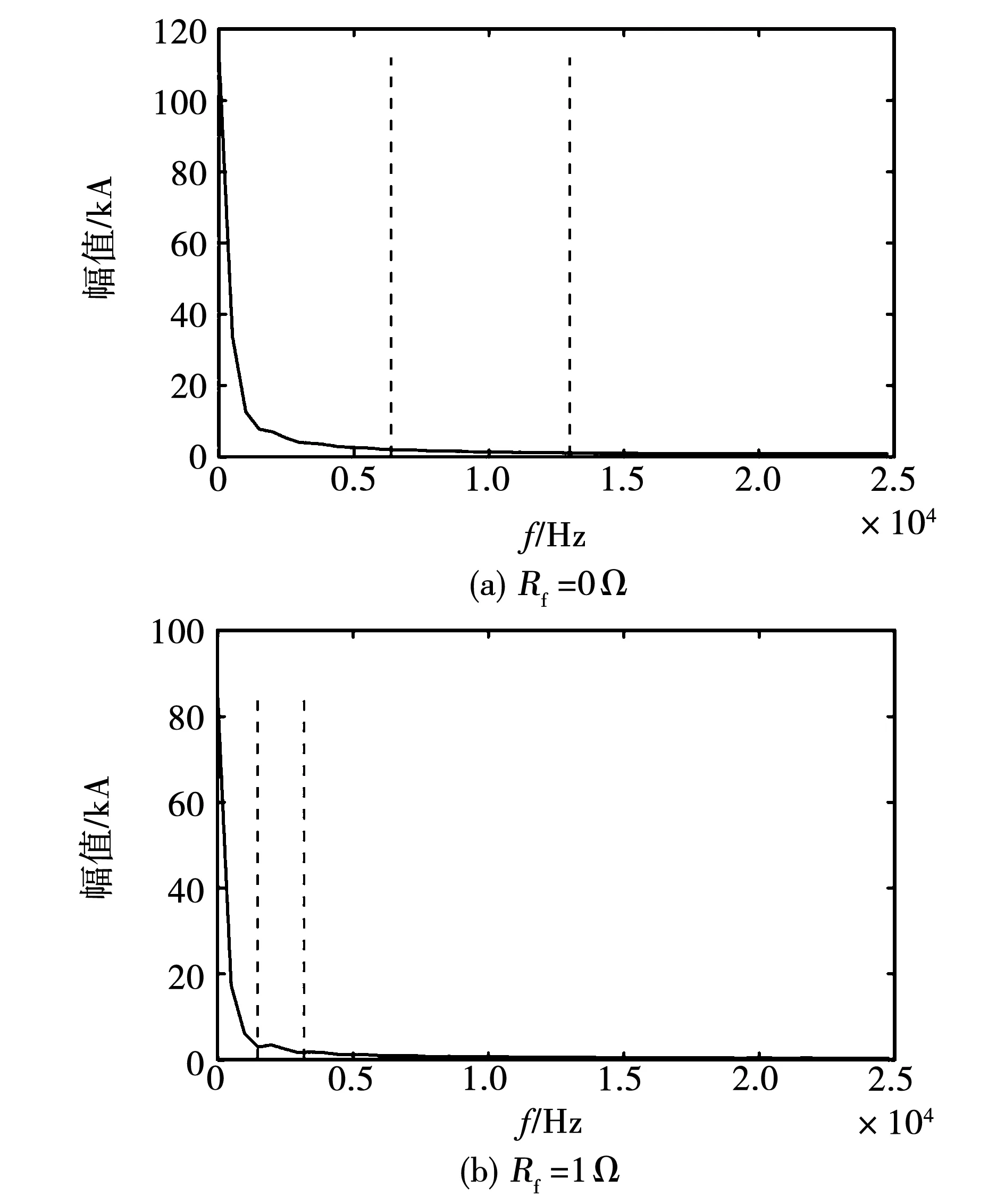
图14 不同过渡电阻情况下傅里叶轴切割结果Fig.14 Segmentation of the Fourier spectrum under different transition resistances

4.4 环境噪声的影响

为验证本文所提的故障检测方案在噪声环境下的适应性，在故障电流信号中添加信噪比为20dB的高斯白噪声，此时考虑换流器VSC2出口处直流线路发生正极金属性故障，本文检测方案的仿真结果如图15所示。

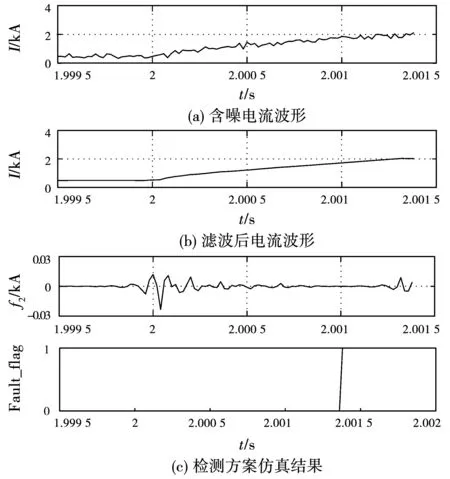
图15 含噪声情况下正极金属性接地故障检测仿真结果Fig.15 Simulation results of positive metallic grounding fault detection in the presence of noise

由图15可知，存在噪声干扰的情况下，采用小波阈值去噪不仅能够有效地去除噪声，而且较好地保留了电流突变点。因此，EWT提取到的高频模态分量仍然能够表征故障，可见，该故障检测方法具备较好的噪声适应能力。

4.5 故障分类仿真验证

对图1所示网络通过仿真得到54组正极接地故障数据，54组负极接地故障数据，12组极间短路故障数据，一共120组数据，其中包含不同的过渡电阻及故障距离，将数据集随机划分成84个训练集，36个测试集。训练集分别用人工数学公式计算、PCA和AE进行故障特征提取，数学公式计算的特征有能量、平均值、标准差、均方根值，其中电压数据去除能量特征，仅保留另外的三个特征。

运用上述三种方法得到的特征及其对应的标签分别训练SVM模型，测试集处理方式同训练集，最后将测试集获得的特征输入对应的SVM模型测试，得到的结果如表3所示。

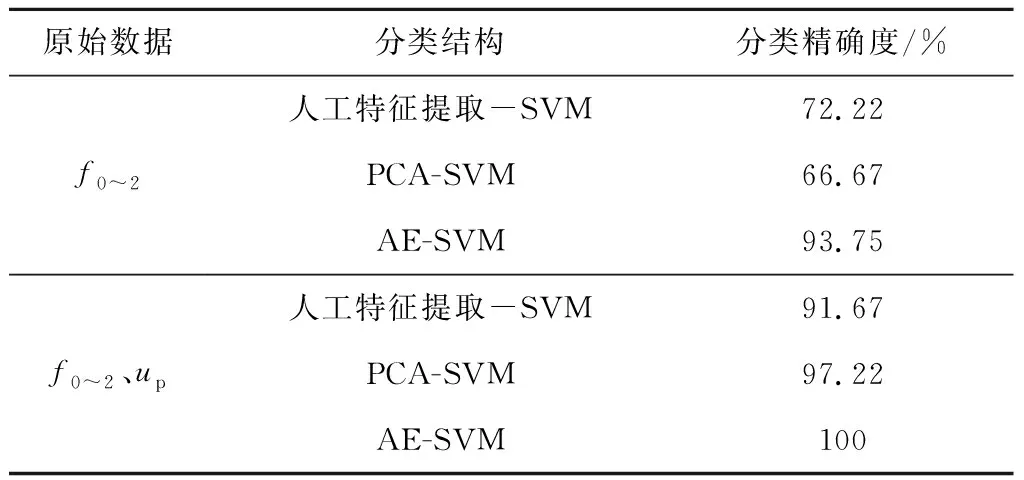
表3 不同特征提取方法故障分类结果对比

由表3可以看出，基于AE特征提取的SVM故障分类明显比采用另外两种特征提取的SVM故障分类准确率高，且原始数据部分加入up确实能够提高故障分类的准确率。

5 结 论

本文依据故障时刻电流突变明显的特点，运用EWT算法分解提取高频分量，并采用希尔伯特变换辨识EWT分解出的信号，从而实现故障的快速检测与可靠识别。理论和仿真均能表明基于EWT特征提取的故障检测方案具有自适应性，检测时间较短，且耐受过渡电阻能力较强。此外，为了方便后续故障隔离，本文运用自动编码器进一步提取故障的深度特征后用SVM进行故障类型识别，避免了手动选择、计算故障特征的繁琐，能够自动提取特征，更显智能化。综上，该故障检测及分类方案在实际工程应用中具有一定价值。