静止液态金属中气泡上升过程实验研究

刘柳，闫红杰，谭智凯，黄正宗，张河杨

(中南大学能源科学与工程学院，湖南长沙，410083)

气泡流广泛存在于能源动力等工业过程中[1−2]。在气泡流中，气泡直径、速度、形状等是影响气泡动力学行为的重要特征参数，也是决定气液相间能量传递的关键因素，因此，系统地研究气泡动力学等基础科学问题可为强化相间传递提供理论指导。目前，针对常规水溶液体系中的气泡流行为已有大量报道，而对于液态金属中气泡动力学行为相关研究远远落后于水溶液体系中的研究，这主要是因为液态金属具有不透明的特点，很难利用基于光学手段的检测技术如高速摄影等对其进行研究。然而，液态金属的物性参数(如密度、表面张力和黏度等)与水溶液体系存在显著差异，因而，研究液态金属中气泡流行为很有必要。一般而言，由于金属的熔点很高，其在高温下才呈现液态的形式，这给研究工作带来了极大困难。因此，目前学术界大多采用常温下呈液态的合金作为研究对象，通过研究常温液态金属中气泡上升行为，明晰液态金属中气泡动力学特性及其与水溶液体系的差异，为指导实际生产过程提供理论依据。

针对液态金属中气泡流行为，在实验手段方面主要采用X射线的方法进行研究。BERTHERAT等[3]将X射线投影成像技术应用于金属铝熔体中气泡运动过程的研究，但受限于当时的成像速度，实验中所得到的气泡图像拖曳严重，失真较大，无法得到气泡的形状、速度、运动轨迹等一系列特征参数。IGUCHI等[4−5]采用X射线投影技术对不同液态金属内气泡进行了有效成像。近年来，很多学者[6−12]采用X射线对液态金属合金GaInSn中气泡动力学行为进行了一系列研究，定性描述了液态金属内气泡的生成过程、气泡浮升过程中运动轨迹的变化以及气泡聚并和破碎过程。

在数值模拟方面，解茂昭等[13]采用VOF 法对单个气泡在液态金属中的运动特性进行了数值计算。刘红等[14]应用基于体跟踪的VOF 方法对金属熔池往复搅拌流场中单个气泡的运动及变形特征进行了数值模拟研究；LIU 等[15−17]采用欧拉双流体模型对液态金属中的气泡上升运动进行了数值模拟。此外，不同学者[18−20]采用侵入式边界法对液态金属中氩气气泡在有磁场和无磁场中的运动规律进行了数值模拟，他们主要关注磁场对气泡运动的影响规律。ZHANG 等[21−23]则采用VOF 方法对磁场作用下单气泡的运动轨迹和运动速度进行了详细研究，阐明了气泡由“之”字形上升转变为螺旋形上升的机理。KRULL 等[24]结合界面追踪法和侵入式边界法的优点，发展了一种新的界面解析方法对液态金属气泡流进行了建模和数值模拟研究，发现采用该方法所得结果和实验结果吻合得非常好。

综上所述，虽然液态金属中气泡流的研究工作取得了一定进展，但是前人的研究大多集中在对液态金属内气泡动力学特性的定性研究，没有定量分析气泡直径、形状等特征参数与水中的异同，以及基于水溶液体系提出的经验关联式是否也适用于液态金属中的气泡流行为。基于此，本文作者采用X 射线显影并结合高速摄影技术对液态金属内的气泡流进行研究，一方面探讨基于水−气系统的气泡特征量纲一参数经验关联式在液态金属中的适用性，另一方面为后续的数值模拟研究提供可靠的实验数据。

1 实验装置及测量方法

实验主体装置为1个小型长方体容器，该容器由丙烯酸玻璃制成，宽度(W)为86 mm，厚度(D)为12 mm，高度(Hc)为144 mm。实验过程中根据液面高度(H)的需求在容器内注入129 mm 的液态金属Ga67In20.5Sn12.5，容器内液相的实际高宽比为1.5。在常温下Ga67In20.5Sn12.5为液态，其主要的物性参数如表1所示[16]。从表1可知：其密度、表面张力和动力黏度分别是常温下水的6.37，7.36 和2.1 倍。实验时采用氩气作为气相，并通过位于容器底面中心位置的医用注射针(外径为1.1 mm、内径为0.785 mm)注入到液态金属中，气泡在注射针的顶部生成、长大并脱离，随后进入液态金属中作浮升运动。气体流量通过质量流量控制器进行测量和控制。由于液态金属GaInSn 不透明，所以，无法直接利用高速摄影技术对气泡进行拍摄并获取其特征参数。本研究借助X 射线显影技术并结合高速摄影对气泡的运动过程进行成像和可视化。图1所示为实验装置及成像系统的示意图[15]。X 射线束通过高功率X 射线源(ISOVOLT 450M1/23-55,GE Co.,US)朝容器表面发射，一部分射线束在穿透容器壁面和液态金属后被吸收，未被吸收的射线继续入射到闪烁屏上，闪烁屏将吸收的射线按射线强弱转换为可见光，可见光由后续的高速摄影系统进行成像并输出到电子计算机中。成像系统由镜头系统(TSO,Thalheim-Spezial-Optik Co.,Germany)和高速摄影仪(Pco.edge，Pco Co.,Germany)组成，成像速度为69 帧/s，曝光时间为3 ms。在实验过程中，保持实验室的温度恒定，通过实验前、实验中和实验后对液相温度进行测量，发现其始终保持在(25±0.5)℃。

表1 液相物性参数Table 1 Physical properties of liquid phase

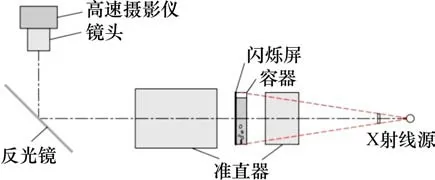
图1 实验装置示意图[15]Fig.1 Schematic of experimental setup[15]

2 数据分析

2.1 图像处理

为了得到气泡直径、纵横比和速度等特征参数，需要对原始气泡图像进行后处理，图像后处理包括以下几步：第一步为去除背景操作，通过将气泡的原始图像减去气体流量为零时的背景图像，去除图像中的背景噪声；第二步为去噪操作，本文采用高斯滤波方法，滤除图像中的随机噪声；第三步为二值化操作，通过选取合适的临界阈值进行二值化，将气泡区域和背景区域分离；最后，通过Matlab 图像处理工具箱中自带的算法提取气泡的特征参数如气泡轮廓、质心等。图像处理的具体过程和效果参见文献[16]。

2.2 气泡特征参数提取

1)气泡当量直径。图2所示为典型的气泡示意图。由于拍摄得到的是气泡的二维投影图像，因此，在计算气泡体积时，需假设拍摄的气泡沿短轴对称，此时，气泡的当量直径计算公式如下：

式中：dB为气泡当量直径；h为气泡的短轴；w为气泡的长轴。

2)气泡变形。气泡变形可通过气泡的短长轴之比(又称纵横比)E表示，计算公式如下：

3)气泡几何形心。气泡的几何形心可通过对二值化填充图像中属于同一气泡的所有像素点的坐标值相加并求平均，将平均值作为气泡的形心。气泡的几何形心坐标可按式(3)进行计算：

式中：i和j分别为气泡区域各像素点的横坐标和纵坐标；N为气泡区域像素的总数；Ω为同一气泡的像素的集合；xc和zc分别为气泡形心的横坐标和纵坐标。

4)气泡上升速度。气液两相流中，气泡的上升速度是一个十分重要的特征参数。由速度的定义可知：

式中：为气泡速度在水平方向上的分量；为气泡速度在垂直方向上的分量；vt为气泡的运动速度；和分别为t时刻气泡形心的横坐标和纵坐标；和分别为t+ Δt时刻气泡形心的横坐标和纵坐标。

图2 气泡示意图Fig.2 Schematic of the bubble

3 结果分析

3.1 气泡直径

图3所示为当气体体积流量(Qg)为400 mL/min、容器高宽比(H/W)为1.5 时气泡上升过程中气泡直径(dB)随容器高度方向(z轴)的变化。

从图3可知：在高度较小的区域内，气泡当量直径随高度增大而增大，这一阶段对应气泡在喷嘴处的长大阶段；当气泡脱离喷嘴后，气泡在液态金属中作浮升运动，气泡当量直径略有增大的趋势。这是由于气泡外部静压减小从而导致气泡发生轻微膨胀。

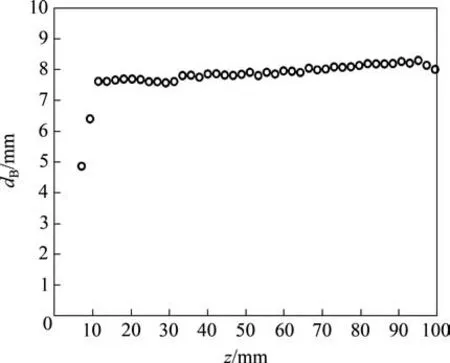
图3 气泡直径dB随容器高度z方向变化规律(H/W=1.5，Qg=400 mL/min)Fig.3 Evolution of bubble diameter along height direction(H/W=1.5,Qg=400 mL/min)

由于液态金属的密度和表面张力等物性参数与水的相差很大，液态金属体系中气泡的生成过程是否与水中相似、气泡脱离直径是否可以通过水−气系统中的经验关联式进行描述是一个值得探讨的问题。另一方面，由于采用欧拉双流体进行数值模拟时，需要气泡直径作为初始条件供相间作用力模型和其他子模型使用，因此，液态金属中气泡生成直径尤为关键。综上可知，必要的实验数据可用来验证经验模型的可靠性，而可靠的模型可帮助预测气泡脱离直径，从而为CFD 提供可靠的初始条件。本研究通过采用X 射线和高速摄影技术实时拍摄气泡的生成过程，得到气泡生成过程的实时图像，进而计算气泡脱离频率从而获得气泡脱离直径与气体流量之间的关系。通过实验结果与文献中预测模型所得结果进行对比，优选出适用于预测液态金属中气泡脱离直径的经验关联式。

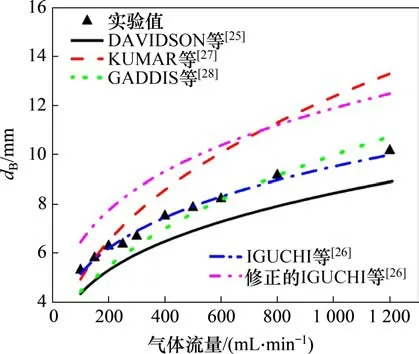
图4 气泡脱离直径dB与气体流量的关系(部分实验值来自文献[16])Fig.4 Bubble diameter as a function of gas flow rate(Some experimental data is from Ref.[16])

图4所示为气体流量在100～1 200 mL/min范围内液态金属GaInSn 中气泡脱离直径与气体流量之间的关系。图4中给出了实验测量值以及各个预测模型得到的预测值。从图4可知：气泡脱离直径随气体流量增大而增大，在流量较小的情况下，两者几乎呈线性关系，而当气体流量较大时，气泡直径增大的趋势减缓。此外，在所有气体流量下，采用DAVIDSON 等[25]关联式所得预测值较实验值偏小，而采用修正的IGUCHI等[26]关联式计算的预测值较实验值偏大。在气体流量较小时，采用KUMAR 等[27]以及GADDIS 等[28]关联式所得预测值略小于实验值，而当气体流量较大时，预测值反而比实验值大。表2所示为各经验关联式预测气泡直径的相对误差及标准差。从表2可知：在所考虑的气体流量范围内，采用原始的IGUCHI等关联式预测的气泡直径与实验值的相对误差仅为−0.002，预测较准确。因此，IGUCHI等经验关联式可作为预测氩气−液态金属中气泡脱离直径的经验公式。

3.2 气泡上升速度及滑移速度

图5所示为气体流量为400 mL/min 时气泡上升速度随高度方向的变化。从图5可见：当气泡脱离喷嘴进入液相后，气泡上升速度不断增大，直到上升到一定高度后，气泡上升速度趋于定值；当气泡上升到靠近液面附近时，由于受到液面的影响，气泡上升速度有略微减小的趋势。

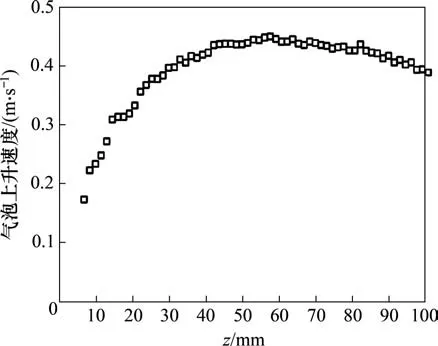
图5 气泡上升速度随高度方向变化规律(H/W=1.5，Qg=400 mL/min)Fig.5 Evolution of bubble rising velocity along height direction(H/W=1.5,Qg=400 mL/min)

由于本研究未测量液相速度，因此，无法得到气泡的滑移速度。通过文献调研发现，ZHANG等[29]对液态金属GaInSn 中单气泡的上升行为进行了实验研究，采用超声多普勒测速技术(UDV)测得了直径在4.3～8.2 mm 范围内的单气泡在上升运动中的滑移速度(见图6)。此外，采用曳力系数经验关联式可计算得到SCHILLER 等[30]、ISHII 等[31]、GRACE等[32]以及TOMIYAMA等[33]经验关联式对气泡曳力系数的预测结果，从而通过曳力与浮力的平衡计算得到气泡的滑移速度，其结果如图6所示。表3给出了各关联式预测的相对误差及标准差。从图6和表3可知：在所考虑的气泡直径范围内，SCHILLER等[30]预测的气泡滑移速度随气泡直径的增大而呈线性增大，且预测值远大于实验值，相对误差达0.986。而GRACE等[32]关联式所得的气泡滑移速度预测值和实验值吻合得非常好，相对误差和标准差分别为−0.054和0.020。此外，ISHII等[31]与TOMIYAMA 等[33]关联式的预测效果相似，气泡滑移速度预测值与实验值之间的误差较小，可用于计算液态金属中气泡滑移速度或曳力系数。

图6 液态金属中单气泡滑移速度Fig.6 Slip velocity of single bubbles rising in liquid metals

表2 各关联式预测气泡直径的相对误差及标准差Table 2 Relative error and standard deviation of bubble diameter with each correlation

表3 各关联式预测气泡滑移速度的相对误差及标准差Table 3 Relative error and standard deviation of bubble slip velocity with each correlation

3.3 气泡变形

图7 气泡纵横比随容器高度变化规律(H/W=1.5)Fig.7 Bubble aspelt ratio evolution with column height(H/W=1.5)

图7(a)所示为气体流量为200 mL/min 时气泡纵横比E随容器高度z的变化。从图7(a)可知：气泡纵横比在喷嘴附近的区域内随高度增大而减小。这是由于气泡脱离喷嘴后作加速运动导致气泡上下压差变大，气泡受到挤压，从而导致纵横比减小。当气泡上升到一定高度后，纵横比趋于定值。图7(b)所示为当气体流量为400 mL/min 时气泡纵横比随容器高度的变化。从图7(b)可知：纵横比在气泡脱离喷嘴后的一段距离内仅微弱减小，当气泡运动到一定高度后，纵横比趋于稳定值。对稳定上升阶段的气泡纵横比进行平均可得到气泡平均纵横比与直径之间的关系，其结果如图8所示。由图8可知：随着气泡直径增大，气泡纵横比呈现缓慢减小的趋势；在所测量的气泡直径范围内，纵横比都保持在0.69以上。

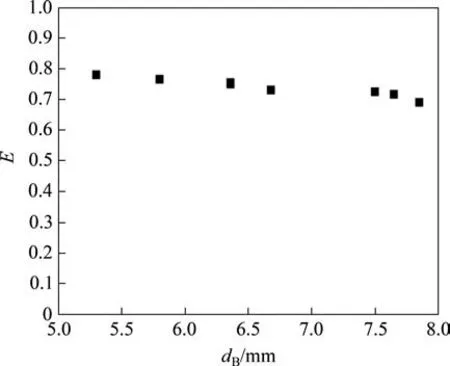
图8 气泡纵横比E与气泡直径dB的关系Fig.8 Relationship between bubble aspect ratio and bubble diameter

图9所示为液态金属内气泡纵横比E与We之间的关系。图9中给出了液态金属中纵横比的实验值与经验关联式的预测值以及水中的实验值集合[34]。由图9可知：气泡纵横比分布在水中纵横比集合的上边界区域。采用MOORE[35]、TAYLOR等[36]以及LIU等[34]的经验关联式预测的结果比实验值小，而WELLEK 等[37]关联式所得预测值与实验值非常吻合。这表明在液态金属中，应考虑气泡惯性力对气泡变形的影响，且可采用WELLEK等[37]的经验关联式对气泡纵横比进行预测。

图10所示为液态金属内气泡纵横比E与Ta(Ta=ReMo0.23)之间的关系。和图9类似，纵横比分布在水中纵横比集合的上边界区域。FAN等[38]以及LIU等[34]的经验关联式预测结果比实验值都小。相对而言，采用TADAKI等[39]关联式所得预测值与实验值的误差最小，但是仍较大。综上所述，采用Ta时，上述经验关联式都不能很好地预测液态金属中气泡纵横比随直径的变化规律。

图9 E与We的关系(蒸馏水和自来水中实验值来自文献[34])Fig.9 Relationship between E and We(The experimental data in water is from Ref.[34])

图10 E与Ta的关系(蒸馏水和自来水中实验值来自文献[34])Fig.10 Relationship between E and Ta(The experimental data in water is from Ref.[34])

4 结论

1)气泡脱离直径随气体流量增大而增大，当气体流量较大时，气泡直径增大的趋势减缓。在所研究的气体流量范围内，采用DAVIDSON 等的关联式所得预测值比实验值偏小，采用修正的IGUCHI等的关联式所得预测值比实验值偏大，采用原始的IGUCHI等的经验关联式预测的气泡直径与实验值很吻合，该经验关联式可作为预测液态金属中气泡脱离直径的经验公式。

2)在所研究的气泡直径范围内，SCHILLER等关联式预测的气泡滑移速度随气泡直径的增大而呈线性增大，且预测值远大于实验值。采用GRACE等关联式所得预测值与实验值吻合得非常好，ISHII 等与TOMIYAMA 等关联式所得预测效果几乎相同，且预测值略大于实验值，这几个经验关联式均可用于预测液态金属中的气泡滑移速度。

3)对于气泡纵横比的预测，MOORE，TAYLOR 等以及LIU 等提出的基于韦伯数We的经验关联式预测的纵横比较实验值都小，WELLEK等关联式所得的预测值与实验值非常吻合。此外，TADAKI 等、FAN 等以及LIU 等提出的基于Ta的经验关联式预测的纵横比都小于实验值。