水煤浆循环流化床锅炉物料平衡特性模型

2021-02-22柯希玮张缦杨海瑞吕俊复张建春刘爱成郭学茂翟永军赵晓星

中南大学学报（自然科学版） 2021年1期

柯希玮，张缦，杨海瑞，吕俊复，张建春，刘爱成，郭学茂，翟永军，赵晓星

(1.清华大学能源与动力工程系，北京，100084；2.太原锅炉集团有限公司，山西太原，030000)

水煤浆具有流动性好、稳定性高、存储易、污染排放少等优点，是一种较为廉价的洁净煤燃烧技术原料。喷雾−悬浮燃烧是应用最广的水煤浆常规燃烧方式之一，但其投资、运行费用较高，且对煤质要求高[1]。随着循环流化床(circulating fluidized bed,CFB)锅炉技术飞速发展，水煤浆循环流化床高效清洁燃烧技术应运而生，目前已有若干台水煤浆CFB 锅炉成功投入商业运行。与普通燃煤链条锅炉或燃煤流化床锅炉相比，水煤浆CFB锅炉热效率较高、综合电耗较低、原始NOx排放很低，配合炉内脱硫后还能大幅降低SO2的原始排放水平，经济和环保效益显著[1−3]。物料循环是CFB 燃烧的基础，水煤浆CFB 锅炉的物料平衡特性与常规燃煤CFB 锅炉相比有很大不同；1)水煤浆中灰分质量分数较低(<10%)；2)水煤浆通常以滴状送入炉膛密相区，燃料粒径为0～300 μm，远小于常规CFB 锅炉的入炉煤粒度要求(1～10 mm)，导致燃料燃烧后的成灰很细；3)水煤浆中水分质量分数很高(>30%)，锅炉烟气量要比同等级常规锅炉大很多，在炉膛截面尺寸相当的前提下，流化风速有所提高。长期实践表明，对于分离器效率较低的传统CFB 锅炉，若入炉燃料灰分过低、颗粒过小，则难以保证良好的物料循环性能，导致炉膛上部颗粒悬浮浓度较低，循环量不足[4]，从而影响炉内传热和受热面布置[5−6]、燃烧和锅炉效率[7−8]、炉内脱硫[9]和NOx排放[10]等，此时，常见的做法是添加河沙或炉渣作为补充床料，或依靠炉内脱硫剂构成主要循环物料，以克服燃料自身灰分的不足。然而，随着分离器技术的进步、分离效率不断提高，CFB 锅炉自身的物料循环性能得到了很大提升。即使不外加床料，纯燃低灰分燃料时也可实现良好的运行性能，这无疑大大拓宽了CFB 锅炉的燃料适应性。了解水煤浆CFB 锅炉的物料平衡特性，探究各设计或运行参数对其影响规律，并寻求最优参数组合，对锅炉的安全高效运行具有重要意义。然而，目前人们对水煤浆CFB 锅炉物料平衡规律的定量研究还比较少。考虑现场实验成本和复杂性，且可参照的实际投运水煤浆CFB 锅炉数量有限，本文作者通过模拟方法对上述问题进行研究。基于物理简化的一维CFB锅炉(1D-CFBB)数学模型利用相对简单的物理或半经验公式描述气固流动过程，具有很高的计算效率，特别适合于大尺度工业设备的模拟和参数研究。RHODES等[11−12]建立了针对小型CFB反应器的一维模型。此后，KLETT 等[13]发展了1DCFBB模型，可应用于具有宽筛分粒径分布特征的CFB 锅炉。YANG 等[14]综合考虑燃料成灰磨耗特性、停留时间和颗粒分层效应，建立了通用的1DCFBB物料平衡模型，并实现对135MWe CFB锅炉的成功预测；BLASZCZUK 等[15]则借助1D-CFBB模型，对世界首台460 MWe 超临界CFB 锅炉的物料平衡进行了模拟。本文作者针对某170 t/h 水煤浆CFB 锅炉建立1D-CFBB 稳态模型，对其物料平衡特性进行了模拟分析，重点探究分离器效率和水煤浆初始粒度的影响规律，以期对水煤浆CFB锅炉的运行优化提供参考。

1 模型建立

1.1 模型基本结构

CFB 锅炉内多呈现出底部密相区鼓泡流态化和上部稀相区快速流态化并存的复合流态[16−17]。与此相对应，在模型中将锅炉由下至上划分为密相区、飞溅区、稀相区和分离器4个部分，并将炉膛沿高度方向划分为若干个小室，如图1所示。忽略炉内横向气固扩散，仅考虑轴向的流动和反混，则各小室具有均一的温度、速度、气固浓度等状态量。另外，很多工程运行结果表明：CFB 锅炉炉内温度分布基本均匀，不会因不同区域受热面布置差异导致吸热量有所区别[16]，故可认为所有小室温度相等，且可作为冷态模型输入参数之一。

图1 1D-CFBB模型锅炉结构Fig.1 Structure of 1D-CFBB model

采用非均匀小室尺寸(网格)划分，以适应不同区域的状态量变化梯度差异(见表1)。值得注意的是，密相区净高度Hden由模型计算得到，在迭代过程中该高度可能发生变化，由此引起密相区和飞溅区单个小室高度ΔH甚至小室数量发生改变，故需考虑迭代前后新、旧小室赋值问题(线性插值)。

本文计算中暂不考虑脱硫石灰石投放对物料平衡的影响，即钙硫比设置为零，则炉内床料绝大部分是水煤浆燃尽后的灰颗粒。因入炉水煤浆及其燃烧后成灰粒径分布较宽，模型中将床料划分为13 个粒径档(5，10，20，30，60，90，120，150，180，210，240，270 和300 μm)。将床料按粒径分档的同时，不同颗粒在炉内的“年龄”(停留时间)也存在差异。因颗粒磨耗等物理过程在起始阶段变化较快，需采用较细年龄划分，以尽可能保证计算精度；后期稳定阶段变化较慢且近似呈线性规律，可适当放宽年龄档，以提高计算效率。本文模型中床料年龄档(时间步长)划分遵循Power law，第k个时间步的步长为

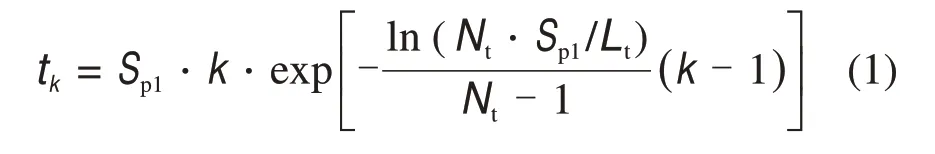
式中：Sp1为首时间步长，s；Lt为计算总时长，s；Nt为总时间步数，在Sp1，Sp2和Lt确定后可随之确定。各时间参数取值见表2，其中，示踪颗粒的引入主要用于物料停留时间的计算，限制最大时间步长不超过Sp2。

表1和表2所示分别为模型中小室和床料年龄划分参数。预备计算表明，表1中的参数选取能够满足计算精度要求，进一步细分对模拟结果影响不大。

表1 模型中小室划分参数Table 1 Model parameters of divisions of cell

1.2 模型方程

锅炉运行处于稳态时，各组灰颗粒(小室i、粒径档j、年龄档k)的质量保持不变，即净质量流率为零：

式中：表示颗粒质量流率，kg/s；下标feed，return，drain，fly，shift，up 和down 分别表示给料、返料、排渣、飞灰、颗粒磨耗、上升流和下降流；和表示因年龄退档导致的质量流率。下面对各项的含义和计算进行简单介绍。

表2 床料年龄划分参数Table 2 Model parameters of divisions of particle age

初始灰分给入流率、返料流率和排渣流率仅分别存在于给煤口、返料口和排渣口(炉底)所在小室。灰颗粒初始粒径分布(即年龄档k=0)可取为本征成灰分布，它不受CFB 运行条件的影响，只与燃料性质有关[14,18]。逃逸出分离器的飞灰流率与分离器效率有关，可用如下模型计算[19]：

式中：ηcyc(j)为对应粒径dp(j)的分级分离效率；D50和D99分别为分离器切割粒径和临界粒径，m；χe为中间参数。D50和D99是表征分离器效率的模型关键输入参数，数值越小，分离效率越高；相差越大，可逃逸出去的飞灰粒径范围越宽。

表示由于颗粒磨耗引起的质量变化，该项会直接影响CFB 锅炉的流化效果，若磨耗突出，则可能使颗粒过细难以被分离器捕捉，导致床料丢失。图2所示为CFB锅炉内颗粒磨耗和退档示意图。本文作者认为流化床内的物料存在3条转变路径：1) 大于临界磨损粒径dcriA的颗粒因表面磨损产生细颗粒，归入细粒径档()；2)大于临界破碎粒径dcriF的颗粒因磨耗使原颗粒粒径减小，退入下一粒径档()；3)停留时间增加，颗粒衰变为下一年龄档()。

由上可知，由4个部分组成：

式中：下标fines，abra 和redu 分别代表该组灰分增加的细颗粒流率(其他大颗粒磨损产生)、因磨损减少的流率和磨耗退档流率。各项的计算方法可参照文献[14]。另外，燃料燃烧成灰和灰颗粒的磨损速率均与燃料特性有关，是模型输入参数之一，需通过实验确定[14]。

年龄档k(或k−1)的颗粒衰变为k+1(或k)档颗粒的质量流率为

图2 CFB锅炉内颗粒磨耗和退档示意图Fig.2 Schematic diagram of ash particle evolution in CFB boiler

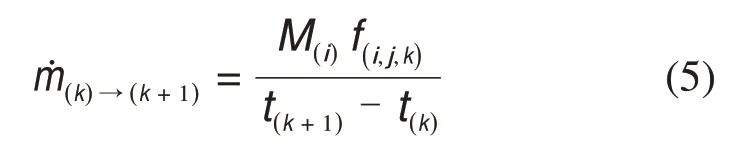
式中：M(i)为第i个小室的床料存量，kg；f(i,j,k)为第(j，k)档颗粒在第i个小室总物料中的质量份额。小室i内所有档颗粒的质量份额之和应等于1。

分离器小室(i=1)内的床料存量与颗粒在分离器内的停留时间有关，可参照LI 等[20]给出的模型计算。提升管小室(i>1)内的床料存量则表示为

式中：Afur(i)为炉膛横截面积，m2；ε(i,j)为截面平均空隙率；ρp(j)为颗粒密度，kg/m3；

本文采用Kunni-Levenspiel(K-L)模型来描述提升管内的空隙率ε分布[12]：

式中：ε(j)(h)为炉膛内固体全部为j档颗粒时高度h处的空隙率；Hden为密相区高度，m；ε∞(j)为炉膛内固体全部为j档颗粒时TDH 高度以上的空隙率；εden(j)为炉膛内固体全部为j档颗粒时密相区内的空隙率；α为衰减指数，m−1；h为布风板以上高度，m。各参数的计算见文献[14]。

小室物料上升流率(除分离器)和下降流率(除炉底小室)可表示为：

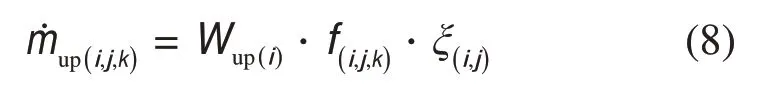
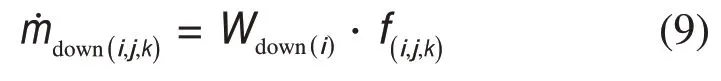
大量实验和模拟研究表明，由于颗粒团的沉降和边壁效应，CFB 稀相区通常呈现“中心稀、边壁浓”的环/核流动结构。不同于稀相气力输送状态下可以用颗粒终端沉降速度表征气固滑移速度及物料上升流率，对循环流化床建模需考虑气固并流上行系统两相结构的不均匀性。忽略提升管颗粒加速效应，本文采用BAI等[22−23]建立的两通道流动模型求解边壁区和核心区的气固流动特征参数，从而得到各小室总上升质量流率Wup，以使以上方程组封闭。

求解该模型可得到环/核气固流动的7 个状态参数(即边壁区厚度xa、核心区空隙率εc、边壁区空隙率εa、核心区气速vg,c、边壁区气速vg,a、核心区颗粒速度vp,c和边壁区颗粒速度vp,a)，进而得到该小室总净质量上升流率Wup：

式中：Ac和Aa分别为炉膛核心区和边壁区横截面积，m2，其与边壁区厚度有关。

1.3 停留时间

当计算收敛(对应于锅炉运行在稳态)时，每个小室内的每一粒径档颗粒在不同年龄档k上达到平衡。由于模型中将床料按年龄分档，将某一粒度不同年龄的颗粒进行统计，其年龄对数量的平均可近似看作该粒度物料的平均停留时间，即

然而，因为存在颗粒磨耗和退档，床料中细颗粒份额增加。根据图2的处理方式，磨耗产生的细颗粒与母颗粒仍属同一年龄档，故按式(11)计算，在小粒径范围内会呈现随着粒径减小停留时间反而增加的非正常计算结果。从另一角度说，被磨耗产生的细颗粒在物质上与母颗粒一致，其在炉内的年龄和母颗粒相同，故对物料直接按份额进行年龄平均，更准确地说是“颗粒年龄”分布。但磨下来的细颗粒粒径已经发生改变，停留时间应重新开始计算。

考虑颗粒磨耗的影响，本文采用“示踪粒子模型”来描述不同粒径档颗粒的停留时间。具体来说，模仿流化床实验中的“示踪粒子法”，在计算中假想往炉内投放一些示踪粒子，其投放位置、颗粒性质等均与灰分相同，但不发生磨耗，只会经历年龄衰退。当所注入的示踪粒子流率很小时，不会改变该锅炉的物料平衡特性，则这些伴随流动的示踪粒子的停留时间可代表对应粒径物料的停留时间。需注意的是，在计算示踪粒子平衡时，床存量、颗粒流率等宏观气固流动参数已由灰平衡方程求解，可作为已知参数使用。

2 模型对象和参数

本文选择某容量为170 t/h 的水煤浆CFB 锅炉作为模拟对象。该锅炉炉膛高33 m、直段宽5 m、深9.3 m，配有2台绝热分离器。前墙布置4个给浆口，给浆口高约1.8 m(以布风板为基线，下同)，并配置相应数量的粒化器，给浆量通过改变给浆泵的转速来调整。采用分级给风，单层二次风对冲布置，二次风口高约4.9 m。炉膛顶部布置高温过热器和水冷屏。锅炉额定蒸汽温度和额定蒸汽压力设计值分别为485 ℃和5.3 MPa，设计热效率超过90%。

与MFC相比，Qt具有明显的优势；文献[15]用Qt替代MFC进行了服务器开发。另外，由于Qt的跨平台特性，可以把Qt用于水下本体Linux系统的软件设计，从而保持在不同硬件的编程一致性。文献[16]实现了在Linux下Qt自定义对话框设计。

入炉水煤浆的工业和元素分析数据见表3。与普通烟煤或无烟煤相比，该水煤浆水分质量分数很高(约35%)，而灰分质量分数较低(<9%)。

燃料的成灰和灰颗粒磨耗性能与燃料自身性质有关，是CFB 锅炉物料平衡计算的关键输入参数之一。目前公开文献中尚未有水煤浆相关结果的报道。从另一角度看，作为煤炭洗选过程中的主要副产品之一，煤泥具有与水煤浆类似的颗粒细(粒径<1 mm，以细颗粒为主)、水分质量分数高(>20%)的特点(尽管煤泥的灰分质量分数通常较高)，因此，本文假设水煤浆的成灰特性与煤泥的相似。张平等[24]借助“静态燃烧+冷态振筛”实验方法获得了煤泥燃烧后灰颗粒的粒度分布情况，发现煤泥在燃烧过程中爆裂现象不明显，成灰粒径分布与煤泥原始粒径分布几乎一致，因此，在模型计算中可考虑直接将入炉煤泥的粒径分布当作初始成灰分布，作为物料平衡计算的输入参数。本文水煤浆CFB 锅炉的计算也采用同样的处理方法。另外，假设灰颗粒的磨耗性能与烟煤燃尽后灰分相似[25]。

表3 某170 t/h CFB锅炉燃用水煤浆的工业和元素分析Table 3 Industial and elemental analyses of CWS used in 170 t/h CFB boiler

本文重点探究分离器效率和水煤浆粒度分布对CFB 锅炉物料平衡的影响规律。分离器效率的计算见式(3)。根据工程经验，D99比D50高4～6 倍，因此，本文固定D99=5D50，通过调整D50在7～28 μm间变化，从而定量分析分离器效率的影响。本文170 t/h CFB锅炉分离器D50约为13 μm。

借助Rosin-Rammler分布函数对水煤浆粒径分布进行描述：

式中：d为颗粒粒径；参数α表征颗粒粒径分布的离散程度，α越小，颗粒粒径分布越宽，其通常与制浆系统性能和原煤性质有关，本文计算中，固定α=3.0；d′为累积质量分数达到63.2%时对应的颗粒粒径，表征颗粒群整体粒度，d′越小，水煤浆中细颗粒份额越多，整体粒度越小。本文通过调整d′为100～200 μm，同时控制粒度范围保持0～300 μm，获得不同水煤浆粒度分布曲线，从而定量分析水煤浆粒度的影响。170 t/h CFB 锅炉设计要求采用粗水煤浆，粒径在100～300µm 间的颗粒质量分数需超过50%，该要求对应的粒径分布也包含在上述设计粒度之内(d′≈160 μm)。

其余运行参数如床温、风量等参照某一实际运行工况确定(基础工况)，如表4所示。在各工况计算中，这些参数保持不变。注意该测试工况下未投放石灰石进行炉内脱硫，即钙硫物质的量比为0。

表4 模型计算主要运行参数Table 4 Main operating parameters in simulation

3 结果与讨论

3.1 锅炉基本运行情况

图3所示为飞灰和循环灰的粒径分布模拟结果，图4所示为床压和截面平均颗粒粒径沿炉膛高度的分布情况，同时给出了相同工况下的部分实炉测试结果。由图3和图4可以看出：模拟值和实测值吻合良好，在一定程度上验证了本文模型的可靠性。

图3 飞灰、循环灰粒径分布Fig.3 Particle size distributions of fly ash and circulating ash

模拟和实测结果均表明，底渣和循环灰的粒径分布相当，这与常规燃煤CFB 锅炉有所不同，后者的底渣粒度一般大于循环灰粒度。从图4可以看出炉内轴向物料粒度分布非常均匀。这是因为入炉水煤浆颗粒都在0～300 μm 之间，而炉内流化风速为5 m/s 左右，若不考虑结渣、颗粒团聚等，几乎所有颗粒都能被烟气携带向上流动，即成灰都是有效床料，均能参与物料循环。图5所示为灰颗粒炉内停留时间与粒径关系。由图5可知：除部分过细颗粒可能逃逸出分离器外，其余较大颗粒的停留时间都很长且几乎相等，不易被排出。

图4 床压和空隙率沿炉膛高度分布Fig.4 Distribution of bed pressure drop and voidage along furnace height

3.2 分离器效率和水煤浆粒度影响

图6～10 所示为在不同分离器效率和初始水煤浆粒度条件下，部分物料平衡相关参数的模拟结果，包括粗/细颗粒炉内停留时间(图6)、飞灰和循环灰中位径(图7)、循环流率(图8)、稀相区平均压降(图9)和飞灰底渣比(图10)，其中，稀相区平均压降反映了炉膛上部物料悬浮浓度。而床料粒度是循环系统性能的主要表征参数，对CFB 锅炉运行具有重要影响，故也称平均床料粒度为床质量。

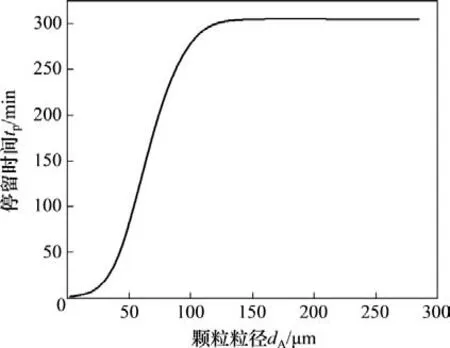
图5 灰颗粒炉内停留时间与粒径关系Fig.5 Variation of ash particle residence time in furnace with particle size

1)横向来看，大部分状态参数与分离器效率近似呈单调关系。

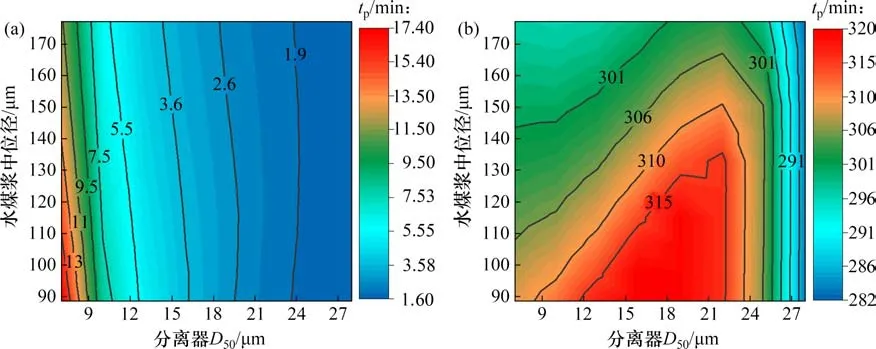
图6 灰颗粒炉内停留时间与分离器效率和水煤浆粒度的关系Fig.6 Effects of cyclone efficiency and CWS particle size on residence time in furnace of ash particles

分离器效率越高，对细颗粒的分离能力越强，细灰逃逸出去的概率就越低，延长了细颗粒在炉内的停留时间；而当炉膛床压降控制不变时，飞灰量的减少会相应使排渣有所增加，加快了粗颗粒的排出。这些作用会使炉内平均床料粒度降低，炉膛上部物料悬浮浓度升高，循环量增大，反映了锅炉整体物料循环性能提升。由于细颗粒的物料平衡对分离器效率更加敏感，因此，水煤浆粒度越细，上述分离器作用越显著。这会在多方面显著改善CFB 锅炉的运行效果。例如，在传热和能量平衡方面，物料悬浮浓度升高增大了受热面表面传热系数，这样，在满足同样吸热量的条件下，可适当减少换热面积或降低床温，而床温降低又有利于避免结渣和降低NOx的原始生成；循环量提高也有利于炉内温度均匀分布，避免局部(特别是炉膛下部)超温。在污染物排放控制方面，提高分离器效率可显著增加细石灰石的停留时间，有利于提高炉内脱硫效率[9]；提高床质量、增加循环量也可使NOx原始排放显著降低[10]，减少尾部烟气脱硫脱硝系统的压力，降低运行成本。此外，分离器效率提高使炉内参与物料循环的有效床料增加，在实际运行中则可适当降低床压降、减小一次风机出力，降低流化风速，锅炉仍可安全稳定运行并保证负荷，但风机电耗即厂用电减少，降低了炉内受热面表面的磨损，使锅炉运行经济性大大提高。

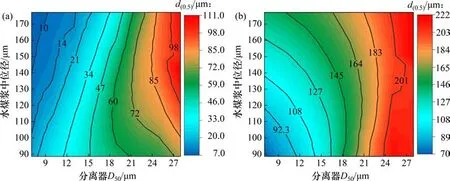
图7 飞灰和循环灰中位径与分离器效率和水煤浆粒度的关系Fig.7 Effects of cyclone efficiency and CWS particle size on d(0.5)of fly ash and circulation ash

图8 循环流率与分离器效率和水煤浆粒度的关系Fig.8 Effects of cyclone efficiency and CWS particle size on circulation rate

图9 稀相区平均压降与分离器效率和水煤浆粒度的关系Fig.9 Effects of cyclone efficiency and CWS particle size on average pressure drop across dilute-phase zone

图10 飞灰底渣比与分离器效率和水煤浆粒度的关系Fig.10 Effects of cyclone efficiency and CWS particle size on ratio of fly ash rate to bottom ash rate

然而，并非所有变量都随分离器效率的改变而单调变化。如图7(b)所示，当初始水煤浆粒度一定时，随着分离器效率提高，粗灰颗粒的炉内停留时间先增加后降低，但总体变化幅度较小(280～320 min)。分离器效率提高，一方面降低了颗粒从分离器逃逸的概率，但另一方面，炉内细颗粒存量增加，为使炉膛床压降(即炉内总物料量)保持不变，排渣率有所增加，使部分大颗粒从底部离开。在飞灰逃逸和炉底排渣这2个因素共同作用下，造成了上述粗颗粒停留时间的非单调变化现象。

2)纵向来看，不同分离器效率下，初始水煤浆粒度对物料平衡特性的影响存在差异。

从模拟结果来看，水煤浆粒度对CFB 锅炉物料平衡特性的具体影响与分离器效率有关。总体来说，当分离器效率很高时，各变量随着水煤浆粒度增加或减小，基本呈单调变化趋势且影响显著；而当分离器效率较低时，水煤浆粒度的改变对物料平衡特性的影响减弱，且部分变量表现出非单调变化趋势。

当分离器效率很高时，大部分细颗粒都能被分离器分离，形成炉内循环。当入炉水煤浆粒度降低时，细灰颗粒质量分数增加，炉内平均床料粒度以及循环灰粒度自然降低，导致炉膛上部物料悬浮浓度升高，循环量增大，从而在一定程度上提高了对粗颗粒的夹带能力，进入分离器以及逃逸出去的粗颗粒量相对增多，使得飞灰总体粒度有所升高。从锅炉总体质量平衡的角度分析，增大入炉水煤浆粒度后，若维持总床压不变，则炉底排渣量增加，使得更多的粗颗粒以底渣的形式排出，故从分离器逃逸出去的粗颗粒量相对减少，导致飞灰平均粒度降低。

而当分离器效率不足时，更多的细颗粒无法被保留而以飞灰的形式逃逸。初始水煤浆中细颗粒质量分数越高，逃逸的细灰就越多，使飞灰平均粒度减小；而能够留在炉内构成稳定循环的灰量就越少，且多为较粗颗粒，从而使循环量降低而循环灰平均粒度增大。但当水煤浆粒度超过一定值后，底渣量不再为零，开始有部分颗粒转从炉底排出(见图10)，此时进一步增大入炉水煤浆粒度，会使循环量略有降低，飞灰和循环灰粒度也均出现小幅度反向变化。也就是说，在低效分离器下，存在最优水煤浆粒度分布使当前条件下的物料循环性能达到最佳，但总体来说，此时水煤浆粒度对锅炉物料平衡特性的影响没有高效分离器的影响显著。

综上所述，高效分离器+细水煤浆的运行参数组合，能够获得最优的物料循环系统性能。另外，此时飞灰底渣比较多，即排渣量较少，因而灰渣物理热损失较少，对冷渣机要求也较低，同样有利于提高锅炉效率和运行经济性。