能效优先的鲁棒功率控制算法
2021-02-22陈威龙梁俊肖楠赵国栋郭子桢
陈威龙,梁俊,肖楠,赵国栋,郭子桢
(1.空军工程大学信息与导航学院,710077,西安;2.中国人民解放军93169部队,136000,沈阳)
随着航天技术和通信技术的不断进步,卫星在人类的生产、生活中发挥着越来越重要的作用,近年来不断受到世界各国的重视。与此同时,5G移动通信技术的不断发展,地面通信频率不断上升,造成了卫星频段与地面频段的冲突日益严重[1]。认知无线电(CR)作为提高频谱利用率的有效手段,受到了国内外的高度重视,认知无线电在卫星通信中的应用能够有效缓解频谱资源紧张的问题[2]。功率控制作为认知无线电技术资源分配的重要手段之一,针对卫星资源受限的特点,有效的功率控制算法是提高能量效率的重要手段[3]。
近年来国内外众多学者对认知网络功率控制算法开展了大量的研究。文献[4]以保障主用户通信质量为目标设计了一种功率控制算法,但网络资源损耗太大;文献[5]为了提高能效,提出了一种可自动调整传输机制,但没考虑信道不确定性影响;文献[6]采用博弈论理论,规范次级用户接入,提高网络能效,但网络容量较小;文献[7]针对认知网络能效,采用最坏情况下的最优解,设计出一种功率控制算法,但没有考虑观测误差;文献[8]基于概率约束提出了一种鲁棒功率控制算法,但是没有考虑能效;文献[9]以次级用户网络吞吐量为目标,并结合能量采集技术提出了一种功率控制算法,却没有考虑次用户之间公平性问题;文献[10]通过对认知用户进行非合作博弈得到了纳什均衡解,但是不适用于卫星场景。
综上所述,上述的功率控制算法大多基于地面认知网络的,而对于卫星认知网络来说,由于通信范围大,信道条件的不确定是卫星认知网络与地面认知网络的最大不同,得到基于理想信道感知的位置信息在卫星认知网络中是很困难的;另一方面,星上资源受限是卫星通信的另一大特点,如何降低功耗,延长工作时间也是亟需解决的问题。基于这两方面,研究能效优先鲁棒功率控制算法是很有必要的。本文基于信道条件不确定导致的距离感知的误差问题,将路径损耗和阴影组合建模为对数正态变量,把功率控制问题转化为约束条件下的最优化问题,同时将概率约束加入约束条件中,引入分式规划与拉格朗日对偶理论,提出了一种能效优先鲁棒功率控制求解算法,最后给出仿真结果与分析。
1 功率控制模型
本文考虑的是星地认知网络多用户共存的功率控制问题,在静止轨道卫星点波束覆盖场景下,星地认知功率控制模型如图1所示,卫星用户为认知用户(SU),地面用户为授权用户(PU)。地面用户与基站通信,卫星用户即认知用户采用定向天线与卫星进行通信,卫星用户采用underlay模式选择某地面用户的频段与其共享。
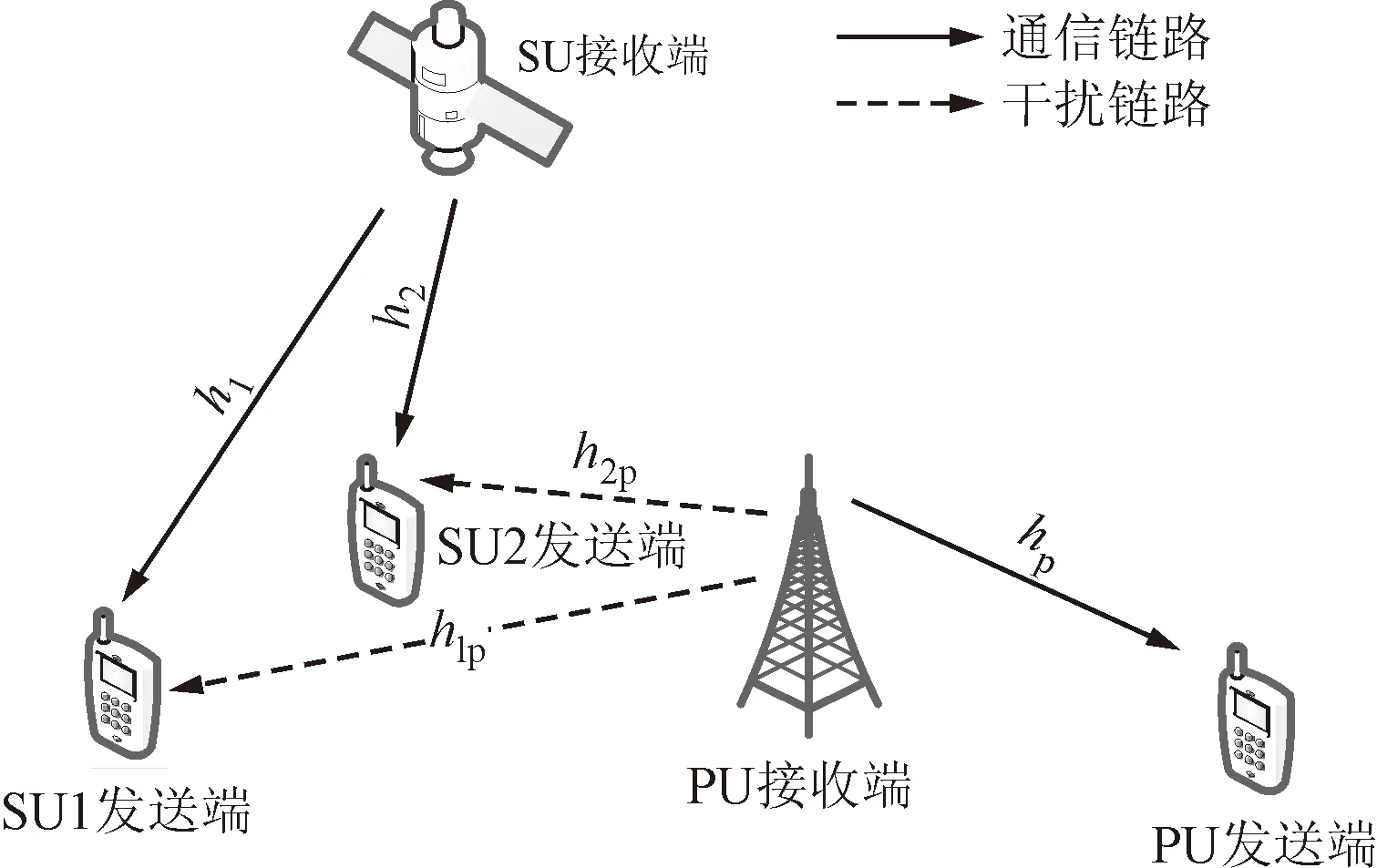
h1、h2—卫星链路增益;h1p、h2p—干扰链路增益;hp—主用户链路增益。
本文的链路增益建模为
(1)


(2)


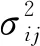
(3)
(4)
因此,卫星用户i的信号干扰噪声比为
(5)

(6)
卫星用户速率为
ni=lb(1+ri)
(7)
在卫星通信中,通常将速率与功率的比值表示为能效。在本文中,为了减少运算复杂度,将能量效率因子e*表示如下
(8)
从(8)式可以看出,能效因子e*越大,单位功率下速率就越高,符合能量效率的定义。
2 功率控制问题建立与优化
2.1 问题建立
在星地认知网络中,功率控制的目的是保证主用户与次级用户能够正常通信的同时满足其他的目标。本文以能效作为功率控制算法的优化目标。由上节可知,能效最大化的优化模型如下所示
(9)

(10)
式中:P(·)为满足括号中条件的概率;αi∈[0,1]表示主用户对次用户干扰的容忍概率;βi∈[0,1]为次用户的中断概率,二者均为提前设置的。可以看出,约束条件C3、C4对认知用户功率有着较好的约束。
不难发现,由于约束条件C3、C4的可行集与信道增益有关,凸凹性无法确定[13],式(1)的求解是很困难的,因此,本文将上述问题转化为确定性的形式。
2.2 问题优化
对于C3,由于hip服从对数高斯分布,将C3重写为
(11)
转化为正态分布
(12)
由正态分布性质并经过整理可得
(13)
式中:Q-1(x)为高斯Q函数的反函数;同理,对于C4,经过简单变换后得到
(14)
根据式(13)和(14),问题式(1)就变换为
(15)
3 感知不确定下能效优先功率控制求解算法
根据上述问题,本文拟采用分式规划和拉格朗日对偶理论,提出了一种感知不确定下能效优先功率控制求解算法——EPCA-SU。
关于分式规划问题求解,根据文献[14],可将式(15)转化为
(16)
定理1优化问题式(16)为凸优化问题。

(17)
显然,式(17)也是大于零的,因此gi(p)是关于pi的凸函数。综上,优化问题(17)为凸优化问题,证毕[16]。
对于凸优化问题(16),采用拉格朗日对偶理论可以很好的求解。根据凸优化理论[17],构建式(16)问题的拉格朗日函数如下
(18)
式中:{λ}和{ξ}为式(17)约束条件C5和C6的拉格朗日乘子。式(16)问题的对偶函数为[18]
(19)
式中
J(pi,λi,ξi)=
(20)
对应式(19)的对偶优化问题为
minD({λ},{ξ})
s.t.λi≤0,ξi≤0
(21)

(22)
式中:e*为能量效率,可采用对分搜索算法更新得到;λ、ξ为拉格朗日因子,可通过次梯度方法更新得到[20]
(23)
(24)
式中κ1和κ2为非负步长因子。
综上,感知不确定下能效优先功率控制求解算法EPCA-SU具体执行步骤如下。
步骤2:设置t=1。
步骤3:由式(23)、式(24)计算λt+1、ξt+1,然后由式(22)计算pt+1。
步骤4:判断|λt+1-λt|≤Δ并且|ξt+1-ξt|≤Δ是否成立,若均成立则执行步骤5,否则t=t+1,转至步骤2。
步骤5:判断|∑lbr-e*∑p|≤Δ是否成立,若成立,则算法结束,{pi}为最终解;若不成立,则转至步骤6。
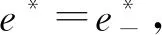
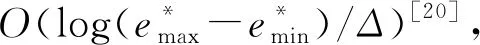
4 仿真与分析

4.1 算法收敛性分析
为了分析所提算法的收敛性,利用上述初始条件进行仿真,结果如图2、图3所示。由图可见,迭代大于5次后,功率和能效均能达到收敛状态。这是由于本文算法包含内外两层循环,收敛速度较快,便于实际应用。

图2 EPCA-SU算法的平均功率随迭代次数变化曲线

图3 EPCA-SU算法的能效因子随迭代次数变化曲线
4.2 算法性能比较
为了证明概率约束对于算法性能的影响,分别改变容忍概率与中断概率,与现有算法进行比较,仿真结果如图4~7所示。

图4 3种算法的平均功率随容忍概率变化v
从图4可以看出,随着容忍概率的减小,主用户需要更高的服务质量,认知用户为了避免对主用户的影响会减小功率以满足概率需求,其中IRPCA算法功率最大,CPBGT算法功率最小。那是因为IRPCA算法没有考虑能效,只考虑在不影响主用户通信的前提下尽量地提升认知用户通信质量,而CPBGT算法基于精确的信道认知情况,没有因考虑信道不确定性的影响而带来的功率消耗。从图5可以看出,IRPCA算法没有考虑能效因此能效因子最低,而对于CPBGT算法,由于信道不确定性而带来通信质量的不稳定,能效因子也较低,因此两算法均低于EPCA-SU算法的能效。

图5 3种算法的能效因子随容忍概率变化曲线
图6和图7分别为认知用户信干比门限为2 dB和4 dB时式(1)中C4的容忍概率βi的变化而引起的功率和能效的变化。随着中断概率的减小,认知用户会增加功率而保持正常通信。与此同时,信干比门限的提升,也会使得功率增加来满足信干比门限并由于门限提升而带来的速率增加会使能效提升。由图6可以看出,随着中断概率的减小,和图5的原因类似,IRPCA算法功率最大,CPBGT算法功率最小;而从图7看出,EPCA-SU算法能效因子高于其他两算法。

图6 3种算法的平均功率随中断概率变化曲线

图7 3种算法的能效因子随中断概率变化曲线


图8 3种算法的算法平均功率随不确定等级变化曲线
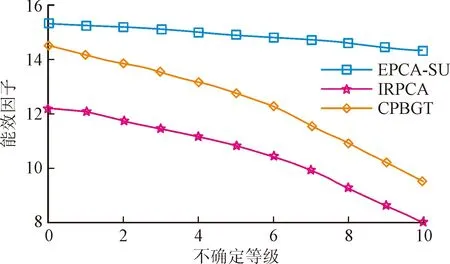
图9 3种算法的算法能效因子随不确定等级变化曲线
5 结束语
本文研究了星地认知网络功率控制中距离感知的误差问题,并将能效作为优化目标,提出了一种能效优先鲁棒功率控制求解算法。仿真结果表明在距离感知误差存在的情况下,该算法能够使认知用户在通信质量和能效方面均能得到有效提高。未来将结合集群智能算法,对密集用户场景进行研究,以满足星地融合网络的发展需求。
