导轨五自由度运动误差的光学与倾角传感器组合测量方法
2021-02-22郭俊康李鑫波李勰
郭俊康,李鑫波,李勰
(1.西安交通大学机械工程学院,710049,西安;2.西安交通大学现代设计及转子轴承系统教育部重点实验室,710049,西安)
高端精密装备的技术水平与研发能力是现代工业中国家竞争力与综合国力的重要因素。直线导轨系统广泛应用于精密机床、半导体制造装备等高端精密装备中,其几何精度与运动精度直接决定着精密装备的整机精度性能[1]。直线导轨系统包含3项线性误差(定位误差、水平和竖直平动误差)和3项姿态误差(俯仰、偏摆和滚转),其中定位误差通常由丝杠等驱动单元决定,并通过光栅进行检测与反馈,其他的五自由度误差取决于导轨、导轨安装基准面的加工误差。对于高端精密装备来说,由于其运动精度要求苛刻,在直线导轨实际装配中往往需要反复测量、拆装、调整[2]。
当前对于直线导轨误差测量多采用激光干涉仪、激光准直仪、电子水平仪等。测量过程中,通常每次只能进行单项误差测量,需要更换测量组件或仪器才可完成多自由度的完全测量。因此,测量手段不足成为了制约精密装备制造效率、质量提升的主要瓶颈问题,直线导轨系统多自由度误差同时测量技术越来越得到国内外研究机构及生产企业的重视[3-4]。
当前多自由度误差同时测量研究的测量原理与方案主要包括3类:基于激光准直的方案、基于激光干涉的方案、基于光栅衍射的方案。文献[5]设计了一个特殊组合棱镜,并提出了和相敏检测技术相结合,测量移动工作台五自由度误差的方法。文献[6-8]对多自由度误差同时测量开展了系统研究,提出将保偏光纤耦合的双频激光器引入到六自由度几何误差测量中,并详细分析了误差串扰和角锥棱镜加工误差对测量精度的影响。文献[9]提出了一种基于几何光学的四自由度几何误差测量方案,设计了一种二维混合调整镜架,以抑制激光漂移对测量结果的影响。文献[10-11]进一步提出了通过测量两平行光束之间的相对位置变化进行滚转角测量的方案,同时实现五自由度同时测量。
在基于激光干涉的测量方面,2016年,文献[12-13]提出了一种六自由度误差同时测量方案,将外差干涉和差分波前技术相结合用于测量工作台的定位误差和俯仰偏摆角误差,利用位敏探测器感知二维直线度误差的变化,以半波片为敏感元件,通过干涉信号的强度变化确定滚转角误差。文献[14-15]在沃拉斯顿棱镜式直线度干涉仪和迈克尔逊干涉仪的基础上,实现了六自由度误差的同时测量。利用光栅衍射特性,文献[16-17]提出一种六自由度同时测量的方法。文献[18]通过反射光栅和参考光栅的±1级衍射光的干涉信号实现了定位误差和竖直直线度误差的同时测量。文献[19]基于几何变换关系和自准直原则,提出了一种新的滚转角测量方法,相较于传统方法,特殊的光学设计使得分辨率提高了一倍。在此基础,进一步开发了一种紧凑的三维角度测量系统。
对比上述3种测量方案,其中基于激光干涉原理的方案,测量精度较高,测量范围大,但测量过程不可断光,对激光器以及采集系统等硬件要求较高,光学结构复杂,成本较高,难以在生产现场规模应用。基于光栅衍射的测量方案,测量范围较小,难以实现光路的快速调节。此外,光栅作为敏感元件,可能因温度影响产生形变引入测量误差。基于准直激光和几何光学的测量方案,结构简单,成本低,具备生产现场规模应用的潜力,但也存在明显的激光漂移对测量精度的直接影响。
本文从制造现场实际需求出发,提出一种基于多传感器融合的导轨五自由度同时测量方案,并提出激光漂移的补偿方案,建立了高效、低成本的测量系统。
1 多传感器融合的直线导轨五自由度测量方法
本文采用多传感器融合方式,建立直线导轨五自由度测量系统。首先对俯仰偏摆角测量、二维直线度测量以及滚转角测量原理进行分析,进而提出误差分离与补偿策略。
1.1 俯仰偏摆角测量
俯仰偏摆角测量光路如图1所示,包括移动单元和固定单元。固定单元固定于静止的安装基准上,发射激光光束并且接收和检测反射光束。移动单元固定于直线导轨系统工作台,用于感知和反馈工作台的位姿变化。
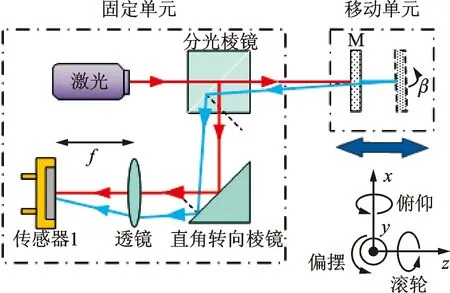
图1 俯仰偏摆角测量光路
光束由激光器出射后通过分光棱镜(BS)分为两条光束,透射光线沿测量方向垂直入射移动单元平面镜,反射后通过分光镜、直角转向棱镜(TM),经过透镜入射到位敏传感器(PSD)上。当移动单元产生俯仰偏摆角度变化时,将引起平面镜空间姿态变化,此时平面反射镜的法向量变为
(1)
式中:α、β分别为移动单元绕x轴和y轴的转动误差。通过空间光追迹法可以得到进入透镜的光线矢量变为[20]
(2)
以初始位置时光束通过透镜中心作为基准,则在测量位置处透镜入射光束产生角度偏移,传感器1检测到光斑相对于参考位置处的水平和竖直位移变化分别为
(3)
式中:d1x为传感器1检测到的光斑水平位移变化;f为透镜焦距;d1y为传感器1检测到光斑的竖直位移变化。移动单元运动中角度变化较小,因此有2α≈tan2α,2β≈tan2β,其角度变化与传感器1位移信号对应关系如下
(4)
1.2 二维直线度测量
二维直线度测量模块光路如图2所示。移动单元在运动中发生平移变化时,安装于其上的角锥棱镜(RR)使准直激光器出射基准光束的反射光束产生相应平移变动,通过安装于固定单元的传感器2检测光斑位置变化,即可得到移动单元相对于准直激光束的平移变动。

图2 二维直线度测量模块光路
图3所示为角锥棱镜位置变化时激光光路变化,其中xyz坐标系为移动单元处于初始基准位置处角锥棱镜坐标系。此时,激光束垂直入射至平面ABC,在3个直角面依次反射,I1、I2、I3、I4分别为反射后相应的光矢量。D0是入射光线和平面ABC的交点,D1、D2、D3依次是光线与3个反射面的交点,D4是出射光线和平面ABC的交点。i、j、k分别为直角面OBC、OAC、OAB的单位法向量,折射进入平面AOB的光线1的单位矢量为
I1=-ai-bj-ck
(5)
式中:a、b、c为入射光线I1在x、y、z轴上相应的方向数。反射光线2、3、4的单位矢量分别为
(6)
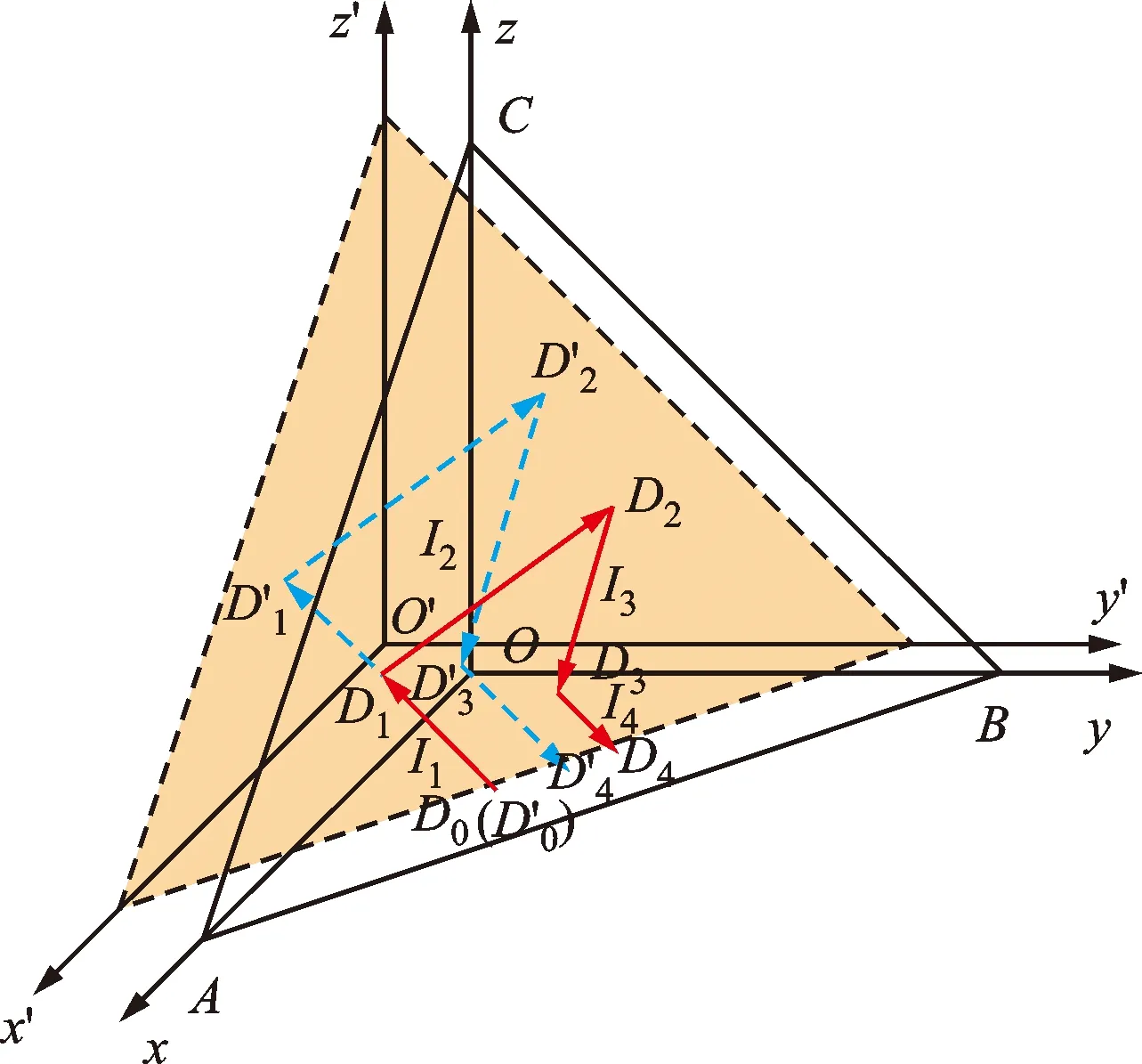
图3 角锥棱镜位置变动时的光路变化
入射点的坐标为D0(x0,y0,z0),则可以得到出射光线与出射面交点的坐标为
(7)
式中:l为OA、OB、OC的距离。当移动单元沿导轨移动时,入射光线不变,固定在其上的角锥棱镜变为O′-x′y′z′。当工作台仅存在平移变化Δx、Δy时,坐标系O′-x′y′z′下入射点坐标变为
(8)
式中Δu、Δv、Δw分别为坐标系O′-x′y′z′相对于坐标系O-xyz的x、y、z轴平动量,则出射点坐标变为
(9)
工作台平动误差与传感器2位移信号光斑平移的映射关系为
(10)
1.3 滚转角测量
目前的光学测量方案中,滚转角测量较为复杂,需要光学元件组合使用,测量仪器体积大、成本高。本文采用倾角传感器对滚转角进行高灵敏度测量,实现了测量方案集成度高与低成本的目标。
1.4 基于共光路的激光漂移分离检测与补偿
激光器发射光束作为测量的几何基准,其稳定性对测量系统精度具有直接影响。激光器在实际工作中,受到谐振腔发热变形、空气介质折射率变化等因素影响,产生激光光束漂移,直接影响测量精度,因此需要对激光漂移进行准确的检测与补偿。激光漂移可分为平漂移、角漂移与随机漂移3种。随机漂移主要与大气湍流和环境波动等因素有关,可通过相关滤波算法抑制随机漂移的影响。角漂移与平漂移主要与激光器的稳定性有关,可以通过分离检测的方法进行补偿[21]。

图4 平漂移分离检测方法
图4、图5所示为本文提出的共光路激光漂移分离检测方法。利用透镜对光束平漂移不敏感而对角漂移敏感的特点,通过传感器3可以得到由于平漂移和角漂移共同引起的光斑位置变化,而通过传感器4分离平漂移和角漂移误差的分离。激光束在x、y方向的平漂移分量分别为εx和εy,激光器本身引起光矢量在x、y方向的角漂移分别为θ1、φ1,环境变化造成的激光束在x、y方向上的角漂移分别为θ2、φ2。
如图4所示,当只存在平漂移误差时,由几何关系可知,在传感器3检测到的光斑位移为d3x=εx,d3y=εy。
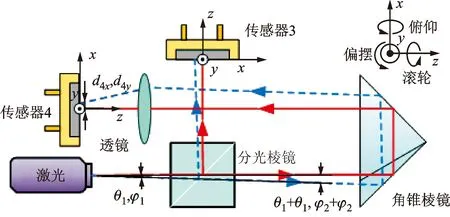
图5 角漂移分离检测方法
如图5所示,当只存在角漂移误差时,在传感器4上检测到的光斑位移为
(11)
1.5 测量方法
综合上述各误差项的测量模型和基于共光路的激光漂移分离检测与补偿方法,得到如图6所示的测量系统总体设计方法。

①—俯仰偏摆测量单元;②—二维直线度测量单元;③—激光漂移测量补偿单元;④—滚转角测量单元。
相较现有的测量仪器,本文测量方法具有以下特点:该测量系统可同时测量直线进给系统五自由度误差,测量效率高;通过共光路分离激光漂移误差,提高了测量系统精度;采用倾角传感器取代了角度误差测量复杂光路元件,测量装置更加简单紧凑,成本显著降低。
2 测量精度的影响因素与补偿
在1.2节直线度测量中,假设移动单元只存在水平和竖直两方向的平移误差。实际上角度误差使光束空间位姿发生变动,对位移测量光路产生串扰,需要进一步研究误差串扰及解耦方法[6]。
如图7所示,建立参考坐标系O1-x1y1z1,测量坐标系O2-x2y2z2。测量初始位置角锥棱镜坐标系为O3-x3y3z3,取角锥棱镜顶点为坐标原点,反射光束如红色实线所示。在后续测量位置,角锥棱镜产生平移和角度变化,坐标系为O4-x4y4z4,光束如蓝色虚线所示。

图7 姿态变化对直线度的串扰
通过坐标变换,可以得到测量位置角锥棱镜坐标系O4-x4y4z4相对于参考坐标系O1-x1y1z1的齐次变换矩阵为
(12)
式中:a、b、c分别为角锥棱镜相对于参考坐标系O1-x1y1z1沿各方向的平移距离;Δx、Δy和α、β、γ分别为坐标系O4-x4y4z4相对于坐标系O3-x3y3z3的平移和旋转分量。
采用下角标i表示入射光斑的相关参数,e表示出射光斑的相关参数,上角标“′”表示角锥棱镜展开后的出射光斑的相关参数。在初始测量基准位置处,入射光斑Mi在O1-x1y1z1中的齐次坐标为
在O3-x3y3z3中的齐次坐标为
出射光斑Me在角锥棱镜展开后的等效出射面中的坐标为
式中:h为角锥棱镜入射面到其锥顶的距离。通过中心对称变换将入射面和出射面重合,实际的出射光斑在O3-x3y3z3的坐标为[20]
式中:M为展开后角锥棱镜出射面与其实际出射面间的中心对称齐次变换矩阵

出射光斑在参考坐标系O1-x1y1z1中坐标为
在测量位置,入射光斑Ni在O1-x1y1z1中的齐次坐标为
通过角锥棱镜展开分析,可以得到在坐标系O1-x1y1z1下,出射光斑Ne在角锥棱镜展开后的等效出射面中的齐次坐标为
式中:n为角锥棱镜材料折射率。出射光斑Ne在实际出射面中的坐标为
与初始基准位置相比,可得传感器2实际测得光斑位移变化为
d2=N1e-M1e=
(13)
角度误差对平移误差测量的串扰为
(14)
式中:偏摆角和滚转角与水平直线度误差耦合,俯仰角和滚转角与竖直直线度误差耦合。通过式(14)可以实现平移误差的有效辨识,消除由移动单元姿态变化和阿贝误差引起的误差串扰。
3 测量系统性能测试实验
3.1 激光漂移补偿方案验证
为了验证1.4节提出的激光漂移分离检测方案的有效性,搭建如图8所示的实验平台,激光器及镜组均安装于隔振气浮平台上,其中传感器1、传感器2用于测量激光器本身的角漂移和平漂移,在距离1 m处通过传感器4检测包含环境干扰的总漂移,传感器3测量角漂移,连续采样4 000 s。
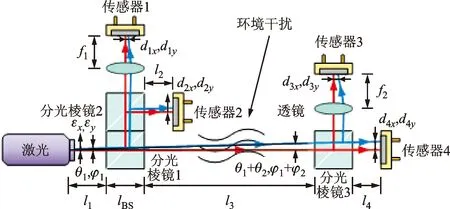
图8 激光漂移分离检测方案验证实验
环境干扰主要包含温度、气压、湿度变化和气流等干扰因素。根据实验光路建立激光束平漂移和角漂移与传感器检测到的光斑位移的对应关系如下
(15)
式中:x1、y1、x2、y2、x3、y3、x4、y4分别是4个传感器在x和y方向测得的光斑位移值;f1、f2分别为传感器1和传感器3前方安装透镜焦距;l1、l2、l3、l4分别为激光经过的各段路径长度;lBS为立方分光棱镜的边长。
利用上述平漂移和角漂移的对应关系,由各个传感器测量结果,对传感器4检测得到漂移量进行补偿,得到1 m位置处经过分离检测并补偿的激光束位移变动为
(16)
图9所示为4 000 s内传感器4上的光斑位置散点图以及通过式(16)分离补偿后的结果,可见光斑漂移明显变小。激光束在x轴漂移变动量标准差为14.50 μm,范围为45.13 μm;y轴漂移变动量标准差为4.77 μm,范围为25.12 μm。经过分离检测并补偿后,x轴漂移范围减小为2.19 μm,标准差为0.39 μm;y轴漂移范围减小为3.02 μm,标准差为0.61 μm。本文提出的分离检测激光漂移的方法通过多个传感器检测光源及环境引起的光束漂移,且可以实现快速补偿,进一步提高了测量系统精度。
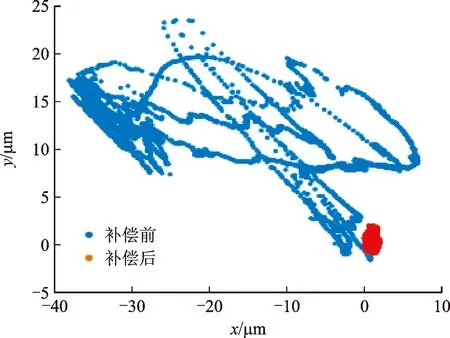
图9 补偿前后光斑位置散点图
3.2 测量系统精度对比实验
为了对本文提出的测量系统性能进行实际测试,采用滚动直线导轨搭建了直线进给系统测试平台。相比于机床的直线进给系统,试验台导轨安装基准面为铣削加工,未经过刮研,几何误差较大,工作台运动误差变化范围大。在每一项误差测量对比实验中,以导轨靠近固定单元处为起始位置,工作台以50 mm的间距沿导轨移动,导轨行程为400 mm,共测量9个位置处的运动单元平移量与角度误差。激光器光束漂移和环境干扰已通过前述补偿光路方案进行补偿,在测量过程中设置传感器采样频率为50 Hz,在每一个测量位置处平稳状态下停留10 s,取该位置处500个测量点的平均值作为该位置测量结果,以减少读数稳定性影响。
(1)俯仰偏摆角对比实验。使用XL-80激光干涉仪(Renishaw,分辨率为0.1 μm/m,精度为±0.000 2×当前测量值±0.5±0.1×测量距离μrad)进行俯仰角和偏摆角误差测量对比实验。实验中,将本文测量系统固定单元和激光干涉仪发射器放置在测试平台两侧,实现工作台运动过程俯仰角和偏摆角误差的同时测量对比,如图10所示。
图11所示为对比实验结果,可以看出两条误差测量结果曲线非常接近,本文系统的测量数据与干涉仪数据基本一致。俯仰角误差最大偏差为3.43″,最小偏差为-5.55″,标准差为2.52″;偏摆角误差最大偏差为4.28″,最小偏差为-3.05″,标准差为2.22″。
(2)平移误差对比实验。采用GEPARD M4激光准直仪(REYTEC,分辨率为0.1 μm,重复性精度为±0.25 μm)进行平移误差测量对比实验,测量方案如图12所示,两套测量系统的激光器同样分别位于导轨平台两侧。在平移误差测量中需要遵循阿贝原则,但由于实际测量中无法保证两个测量系统基准光路重合,需要进一步考虑角度误差进行修正对比。

图12 平移误差对比实验方案
实验结果如图13所示,可以看出,两条测量曲线的趋势一致,本文测量系统与激光准直仪相比,水平平移误差最大偏差为2.03 μm,最小偏差为-2.47 μm,标准差为1.40 μm;竖直平移误差最大偏差为1.30 μm,最小偏差为-1.92 μm,标准差为0.96 μm。
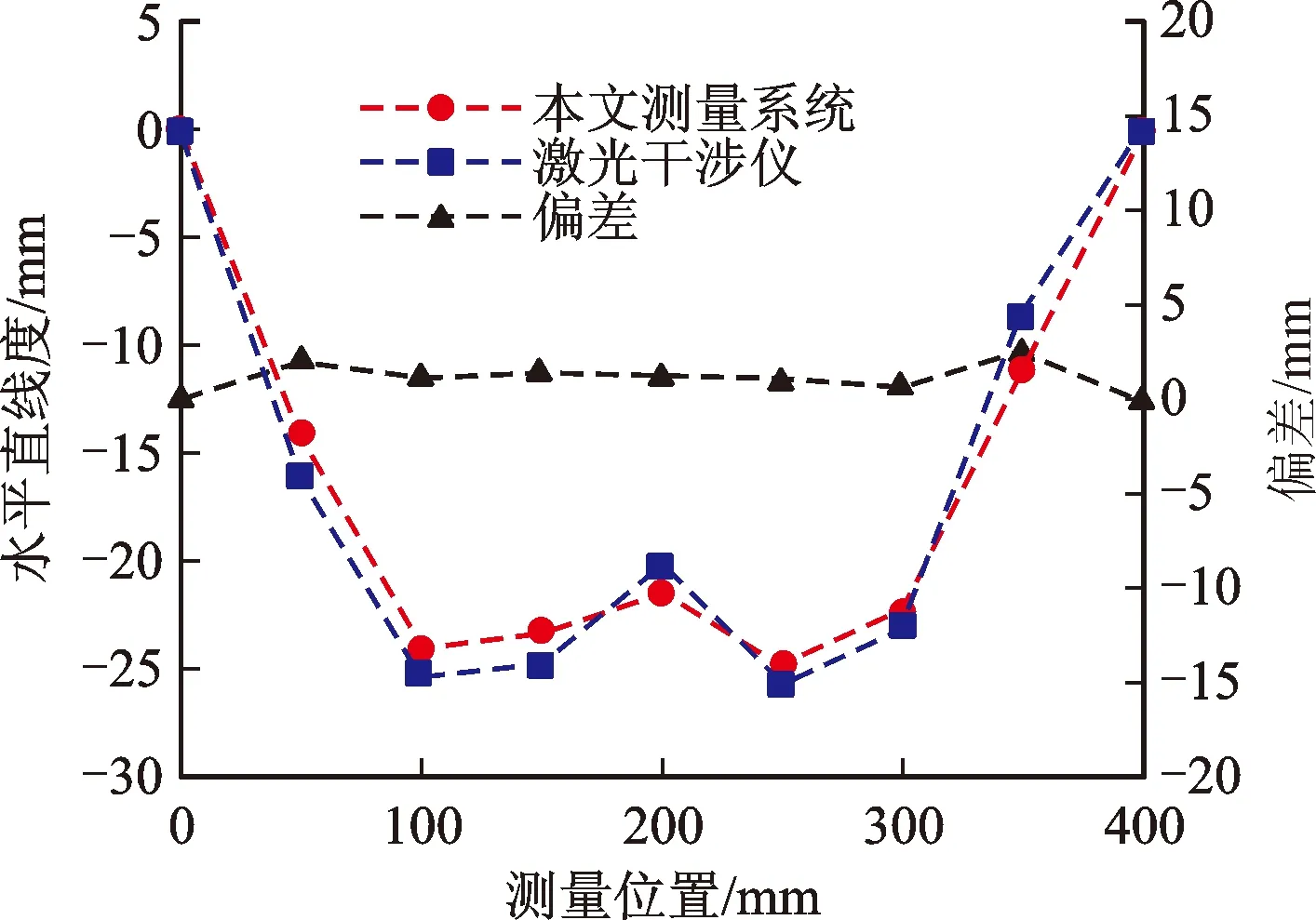
(a)水平平移误差
(3)滚转角对比实验。采用BLUELEVEL高精度电子水平仪(Wyler,分辨率为0.2″,精度为1%×当前测量值+最小数显位)进行滚转角对比实验。实验中,将移动测量单元和电子水平仪放置在工作台上,同时对直线进给系统的滚转角误差进行测量,如图14所示。

图14 滚转角误差对比实验方案
实验结果如图15所示,与电子水平仪相比,滚转角误差测量的最大偏差为1.70″,最小偏差为-2.21″,标准差为1.59″。
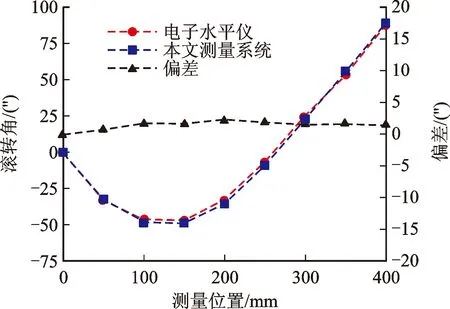
图15 滚转角对比实验结果
通过上述对比实验可以看出,直线进给系统的五自由度测量当前需要激光干涉仪、准直仪、水平仪等多种测量仪器的综合使用,测量时间长。雷尼绍公司的多光束激光干涉仪XM-60通过四光束干涉测量和光学偏摆测量可实现任意方向6个自由度的同时测量,结构紧凑,其主要参数与本文测量系统对比如表1所示。
由于本文提出的测量系统采用结构简单、元件成本更低的几何光学测量原理,其测量分辨率与多光束激光干涉仪存在差距,但相比于现有文献报道的多自由度测量方案,结构更加紧凑,成本低。通过误差测量对比试验,本文系统测量精度可以满足较高精度直线进给系统运动误差要求。
4 结 论
(1)本文提出了一种基于光学与倾角传感器组合的直线导轨系统五自由度运动误差测量原理与方法,通过误差解耦,消除各自由度误差串扰。建立了基于共光路的激光漂移分离与补偿方案,通过实验验证了可将激光漂移减小到3 μm范围。
(2)通过与激光干涉仪、激光准直仪、电子水平仪测量结果对比,本文提出的测量系统测量偏差满足工程需求,且可实现五自由度同时测量,测量装置成本显著降低。
