引入深度强化学习思想的脑-机协作精密操控方法

张腾,张小栋,2,张英杰,2,陆竹风,朱文静,蒋永玉

(1.西安交通大学机械工程学院,710049,西安;2.西安交通大学陕西省智能机器人重点实验室,710049,西安)

随着人工智能技术的发展,对具有仿人高级认知能力、能在复杂环境中执行非设定任务的智能机器人的需求日趋紧迫,但是单凭人工智能技术尚无法满足。因此,研究者提出了人-机智能融合方法,该方法结合了人的直观推理、自组织学习以及处理非结构化信息的能力,同时兼具机器强大的计算能力、存储容量和不知疲倦的特性,目的在于充分发挥人和机器两者的优势。随着人-机智能融合系统所面临任务和场景的复杂化,研究者在人-机智能融合的基础之上,提出了一系列脑-机智能融合增强技术,例如脑控汽车[1]、脑控无人机[2]、脑控外骨骼机器人[3]、脑控轮椅[4]以及脑控假肢[5-6]等。然而,在精密操控领域(例如医疗、军事和太空探索等),与肢体操控方式相比,脑控方式在稳定性和安全性上还存在风险。因此,目前在精密操控领域依然以人的肢体操控方式为主,例如手术机器人[7]、排爆机器人[8]、武器操控系统[9]以及在轨对星球表面遥操作系统[10]等。经过研究发现,在人-机交互的精密操控领域,由于缺乏操控者和机器之间信息的双向交互,无法实现对操控者意图的精密感知;同时,由于人脑精神状态(例如疲劳、专注度和脑力负荷等)的变化会影响肢体操控的精度和安全性。

对此,有关学者在精密操控领域引入脑-机接口技术,在不改变肢体操控方式的前提下,使用表面脑电信号(EEG)检测操控者的精神状态,并根据操控者的精神状态对机器人的指令进行补偿调控,以实现精密操控。目前国内外相关的研究主要分为两个方面:操控者精神状态检测研究和基于精神状态的补偿控制研究。

在操控者精神状态检测研究方面:Dijksterhuis等要求驾驶员在驾驶任务中,执行不同难度等级的驾驶任务,利用EEG识别驾驶员的脑力负荷,平均识别精度达到95%[11];朱成杰等提出在飞行任务中EEG的各种节律波会随着飞行员疲劳状态和脑力负荷的变化而改变,因此利用EEG检测技术可有效识别飞行员的疲劳状态和脑力负荷[12];Wang等在多属性任务组(MATB)中,要求受试者执行3种难度等级的MATB任务,以2～100 Hz的EEG傅里叶变换系数为特征,对受试者脑力负荷的识别精度进行测试,结果表明其识别精度可达80%左右[13]。上述研究均证明了EEG可有效地反映操控者的精神状态,但是目前的研究还仅停留在精神状态的检测和识别方法上,并未考虑精神状态和操控品质之间的联系。

在基于精神状态的补偿控制研究方面:Wilson提出了一种自适应自动化系统,该系统可根据人的脑力负荷动态分配机器和人之间的任务属性和等级,目的在于提高操控品质[14];Jia等在遥操作任务下,根据操控者的精神状态实时调控机器人的速度和响应时间参数,目的在于提高操控的精度和安全性[15];杨少增采用模糊建模方法建立了人的精神状态估计和预测模型,以使操作员所承担的任务与其当前的状态两者相匹配[16]。然而,目前大多数的研究,多预先设定所谓的精神状态“好与坏”的表现特征,从而主观认为当检测到精神状态“好”的特征时就增加任务难度,反之则降低任务难度,忽略了精神状态的多样性(尤其是在跨个体和跨时间角度上精神状态的多样性更强),从而导致精神状态和控制指令之间失匹配,无法有效提高操控品质和安全性。

综合上述两方面的研究现状,发现两个方面多单独研究,没有形成一体化的脑-机协作模型;同时,基于精神状态的补偿控制方面主观性强,未考虑到精神状态的多样性。因此,针对人-机交互精密操控领域亟待解决的这两大基础共性问题,本文以机器人最基本的轨迹跟踪任务为应用目标,提出一种引入深度强化学习思想的脑-机协作精密操控方法。首先结合人在上层规划与机器在精细控制上的优势,提出双环路的人-机之间信息交互机制,进而建立一种基于深度强化学习的一体化的脑-机协作方法模型;然后设计相应的精神状态实时监控方法,开发一套具有工程应用价值的脑-机协作精密操控算法;最后拟搭建具有3种难度等级的轨迹跟踪虚拟环境,并设计训练实验、验证实验和对照实验,以验证脑-机协作精密操控方法的有效性。

1 双环路人机信息交互机制

本文融合人在上层规划与机器在精细控制上的各自优势,提出了由主动操控环路和被动调控环路组成的双环路人-机信息交互机制,如图1所示。考虑到人在上层决策、突发情况处理方面的优势,因此在轨迹跟踪任务中,使操控者对机器人方向指令的控制具有优先权。在主动操控环路中,操控者通过操控装置发送方向指令给机器人,同时通过视觉等信息对机器人的运行状态进行监督,实时地调整方向指令,并对突发的错误进行纠正;考虑到机器在精细控制上的优势,使计算机对机器人速度指令的控制具有优先权。在被动调控环路中,引入深度强化学习思想[17],创新性的将操控者大脑作为环境对象,将控制算法作为智能体对象,建立一体化脑-机协作方法模型,其以反应操控者精神状态的EEG微分熵特征作为输入,以机器人速度指令作为输出。模型经过多次自主训练,将多样性的精神状态和机器人的控制指令相匹配,从而促进人-机之间相互适应和监督,实现人脑和计算机协同合作(简称脑-机协作)执行精密操控任务。

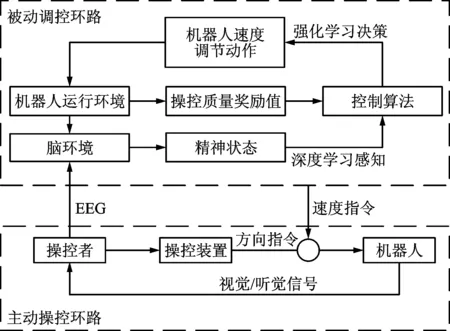
图1 双环路人机信息交互机制

在一体化脑-机协作模型训练阶段:操控者通过肢体操控方式发送方向指令的同时,脑电设备采集大脑EEG并传给控制算法,控制算法根据当前EEG生成相应的速度指令,机器人根据方向指令和速度指令执行相应任务。此外,操控者在监视和操控机器人时,会引发精神状态变化(例如:机器人犯错会引发大脑警觉;操控任务复杂且长时间执行任务会由于高脑力负荷而引发大脑疲劳;操控任务过于单一会引发大脑专注度下降等)。精神状态的变化会影响肢体操控的精度和安全性,因此脑电采集设备将EEG实时输入控制算法,控制算法及时决策机器人的速度指令。机器人每执行一次完整实验,控制算法会根据任务完成精度和时间两个指标计算奖励值并更新模型中网络参数,直到控制算法中网络模型收敛并达到奖励最大化。在一体化脑-机协作模型验证阶段:将训练好的控制算法参数导入到机器人的控制器中,通过所建立深度神经网络感知操控者精神状态,利用强化学习方法根据精神状态决策机器人的速度指令,从而实现脑-机协作精密操控。此模型利用深度强化学习理论建立脑-机之间一体化的架构,真正实现了双环路的交互机制。

2 脑-机协作方法数学模型

本文所建立的脑-机协作方法模型属于“免模型强化学习”范畴,因此,本文根据蒙特卡罗采样原理[18],从任意起始精神状态s1出发,使用某种策略G进行采样,执行该策略i步并获得轨迹τ,详细的采样过程如图2所示。获得采样轨迹τ的概率可由下式表示

pθ(τ)=p(s1)pθ(a1|s1)p(s2|s1,a1)pθ(a2|s2)

p(s3|s2,a2)…pθ(ai|si)p(si+1|si,ai)=

(1)

式中:si(i=1,…,k)表示第i时刻的精神状态(以下简称状态);ai(i=1,…,k)表示第i时刻的机器人速度调节动作(以下简称动作);pθ(τ)是指给定策略神经网络参数θ的情况下,出现采样轨迹τ的概率;p(s1)是指初始状态s1出现的概率;pθ(ai|si)是指给定当前状态si,采取动作ai的概率;p(si+1|si,ai)是指采取当前状态si和动作ai之后,基于该条件概率返回下一个状态si+1的概率。

图2 脑-机协作方法模型蒙特卡罗采样示意图

对于某一个采样轨迹τ,可以得到其对应的奖励,通过优化控制算法,可以得到不同的奖励。由于控制算法采取的动作以及出现某一个状态是随机的,最终的目标是找到一个具有最大期望奖励的策略神经网络参数,因此目标函数如下

(2)

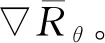
(3)

式中:n为采样次数;N为总采样数。由式(1)和式(3)可得

(4)

为了使奖励值R(τ)不受采样随机性的影响,这里引入一个基准线b,因此梯度公式优化为

(5)

式中:精神状态si由所采集到的EEG的微分熵特征来表示;机器人速度指令ai由神经网络的输出值而获得;奖励值R根据机器人执行任务品质评分获得,详细介绍见第3节。首先将原始EEG进行滤波和降采样预处理;其次进行小波分解与重构;最后计算微分熵特征。其中,小波分解与重构过程如下

(6)

式中:xj表示第j个频带的EEG;L表示分解层数;Aj表示近似分量;Dj表示不同尺度的细节分量[19]。

对于固定长度的脑电序列可进行如下近似处理计算微分熵[20]

(7)

式中:s(x)表示微分熵特征值;f(x)表示时间序列的概率密度函数;μ和σ分别表示高斯分布的均值和标准差。

最后,利用梯度下降法更新策略神经网络的参数θ,直到网络模型收敛,具体算法如下

(8)

3 脑-机协作精密操控算法

为了将反映精神状态的实时EEG输入给控制算法的模型,每次实验总是提取计算机内存中最后1 000 ms长的EEG作为输入信号。对输入信号的处理主要分为3个阶段:①预处理,采用4阶巴特沃兹带通滤波器处理EEG,保留0.5～45.0 Hz的频带信号,然后进行降采样处理;②小波变换处理,采用5阶Daubechies小波基函数,从EEG中分解并重构出5种节律波,小波分解原理如图3所示;③特征提取,分别计算32个通道的5种节律波的微分熵特征,形成160维的特征数据矩阵S,S即作为反映操控者精神状态的特征输入给脑-机协作方法模型。

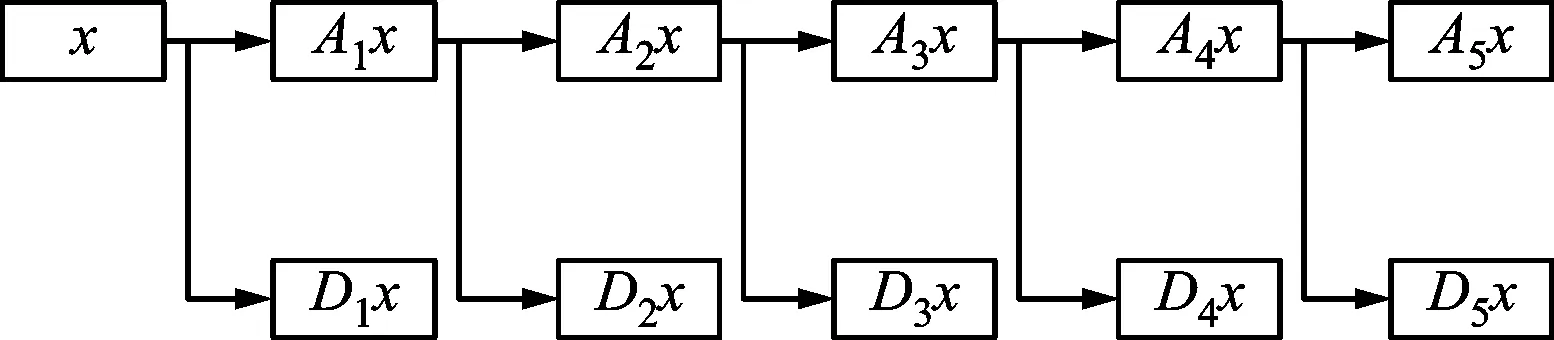
图3 5层小波分解原理图

在脑-机协作方法模型中为了兼顾算法精度和响应速度,本文建立了3层全连接神经网络,详细的网络拓扑结构如图4所示。网络输入为精神状态(即表征精神状态的特征矩阵S),输出为机器人速度指令ai。其中输入层有160个神经元,隐含层有80个神经元,输出层有4个神经元,分别表示4种无量纲的速度等级(0.5、1、2和2.5)。隐含层采用tanh激活函数[21],输出层经过softmax函数[22]处理之后,利用随机策略选择速度指令ai,其中概率值高的被选中几率高,反之,被选中的几率低,目的在于符合“探索”和“利用”平衡的原则(EEb),从而获得最大的奖励。奖励值R由轨迹跟踪精度和完成时间两项指标组成,详细表达式如下

(9)

式中:Y表示机器人的行走轨迹;O表示目标轨迹;T表示每实验一次完成的时间;g表示时间系数;M表示整个轨迹的总步数。将数据组(s,a,R)输入给目标函数,根据自适应矩估计梯度下降法(ADAM)[23]更新神经网络参数,其中学习率(rL)设置为0.001。训练阶段每执行一次完整实验,模型更新一次,直到模型收敛为止。

图4 脑-机协作方法模型参数更新原理图

4 实验验证分析

4.1 环境平台及实验系统创建

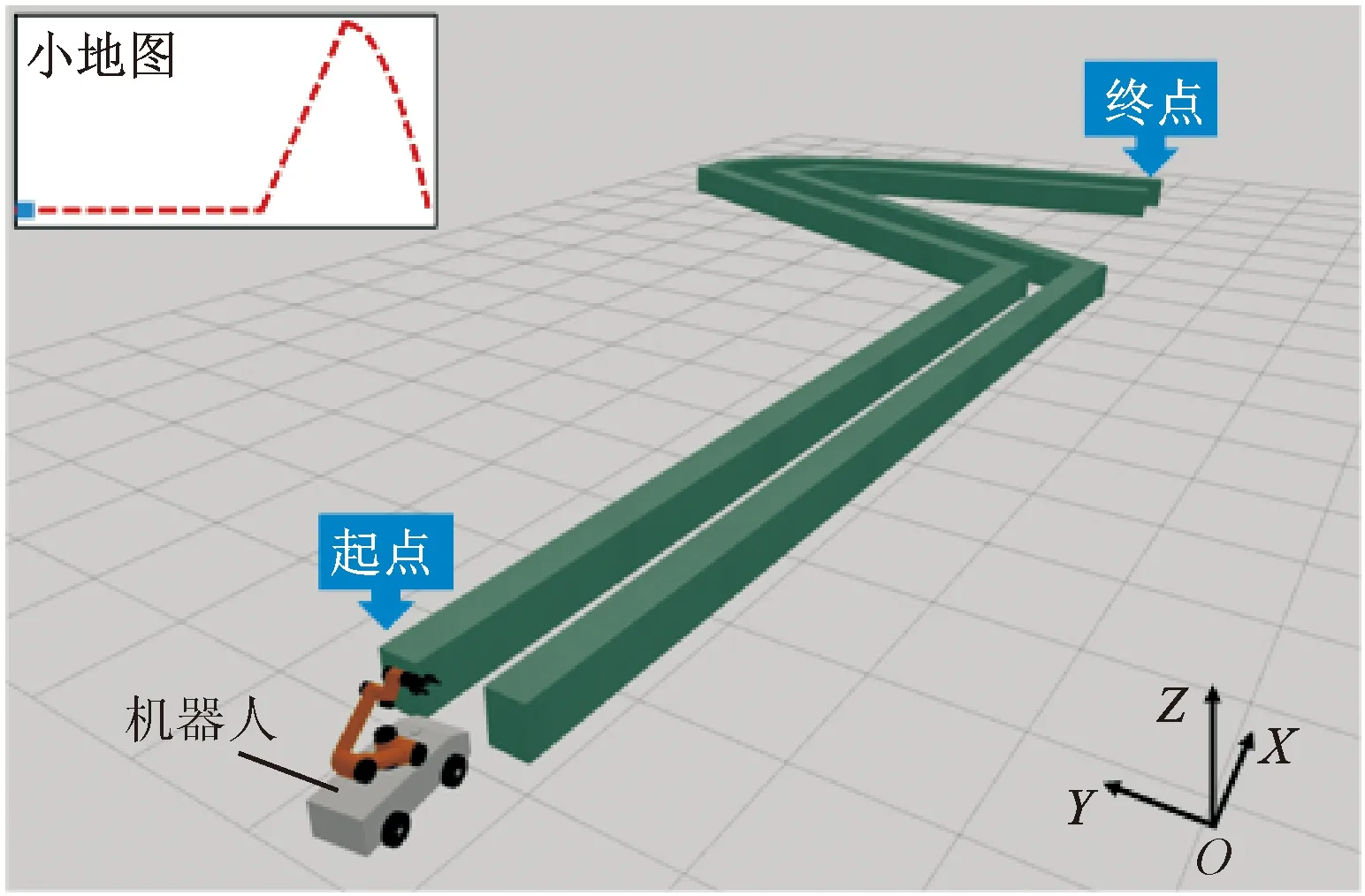
(a)轨迹跟踪环境

为了验证脑-机协作方法的有效性,本文以精密操控机器人执行轨迹跟踪任务为例。此任务作为远程操控特种机器人排爆、消防、救援等领域关键的任务之一受到广泛关注。本实验搭建了一个脑-机协作操控的轨迹跟踪环境平台,具体如图5a所示,操控者通过鼠标控制机器人执行轨迹跟踪任务。为了增加实验的多样性,设计了水平直线、斜线和曲线3种难度等级的轨迹。实验场景如图5b所示,其中机器人的方向指令由操控者通过鼠标控制,速度指令由计算机中的控制算法根据操控者精神状态的变化不断地调节,机器人结合方向和速度两项指令,执行规定的任务。在轨迹跟踪任务中,操控者通过观察机器人的运行状态,不断调整方向指令,同时计算机中的控制算法通过检测人脑精神状态实时调整机器人的速度指令,从而通过脑-机协作,实现对机器人的精密操控。每完成一次完整实验,控制算法会记录机器人行走的轨迹和完成时间,并根据此两项指标计算奖励值,具体计算方法如式(9)。控制算法中的神经网络模型根据奖励值更新参数,直到神经网络模型收敛。

实验采用博睿康公司(Neuracle)开发的32通道的脑电采集设备,如图6a所示,其采样频率为1 000 Hz,通过无线路由与电脑相连。本实验按照国际10-20系统选择脑电通道,具体电极分布位置如图6b所示。

(a)采集设备

4.2 受试者及实验步骤

本次实验共有5名受试者(标记为Sub1～Sub5,其中1名为女性),年龄均在23～30岁,无精神疾病史,视力或矫正视力在1.0以上。实验过程中要求受试者静坐在电脑屏幕前,通过鼠标控制屏幕中的机器人执行轨迹跟踪的任务。每完成3种预设轨迹(水平直线、斜线及曲线)的跟踪任务即为完成一次实验的全过程。实验共分为3个阶段,分别为训练阶段、验证阶段和对照阶段。训练阶段用来训练脑-机协作方法模型参数;验证阶段是将训练好的脑-机协作方法模型输入到机器人的控制器中,进行验证实验;对照阶段不使用脑-机协作方法(即传统方法),其他设置与验证阶段相同。训练阶段实验执行65次,前5次用来练习轨迹跟踪任务,防止因为操作的熟练度不同而影响实验结果,后60次为正式实验。每20次中间有1 min的休息时间。对照阶段实验和验证阶段实验各执行25次,前5次均用来练习轨迹跟踪任务,后20次为正式实验,具体实验步骤如图7所示。

考虑到精神状态的多样性,每名受试者在一天之中不同的时间段进行实验(例如Sub1的实验时间为20:00～22:00;Sub2和Sub5的实验时间为9:00～11:00;Sub3的实验时间为14:30～16:30;Sub4的实验时间为16:30～18:30),适当增加了表征精神状态的EEG数据的多样性。考虑到每名受试者实验的舒适度,实验时长为2 h。

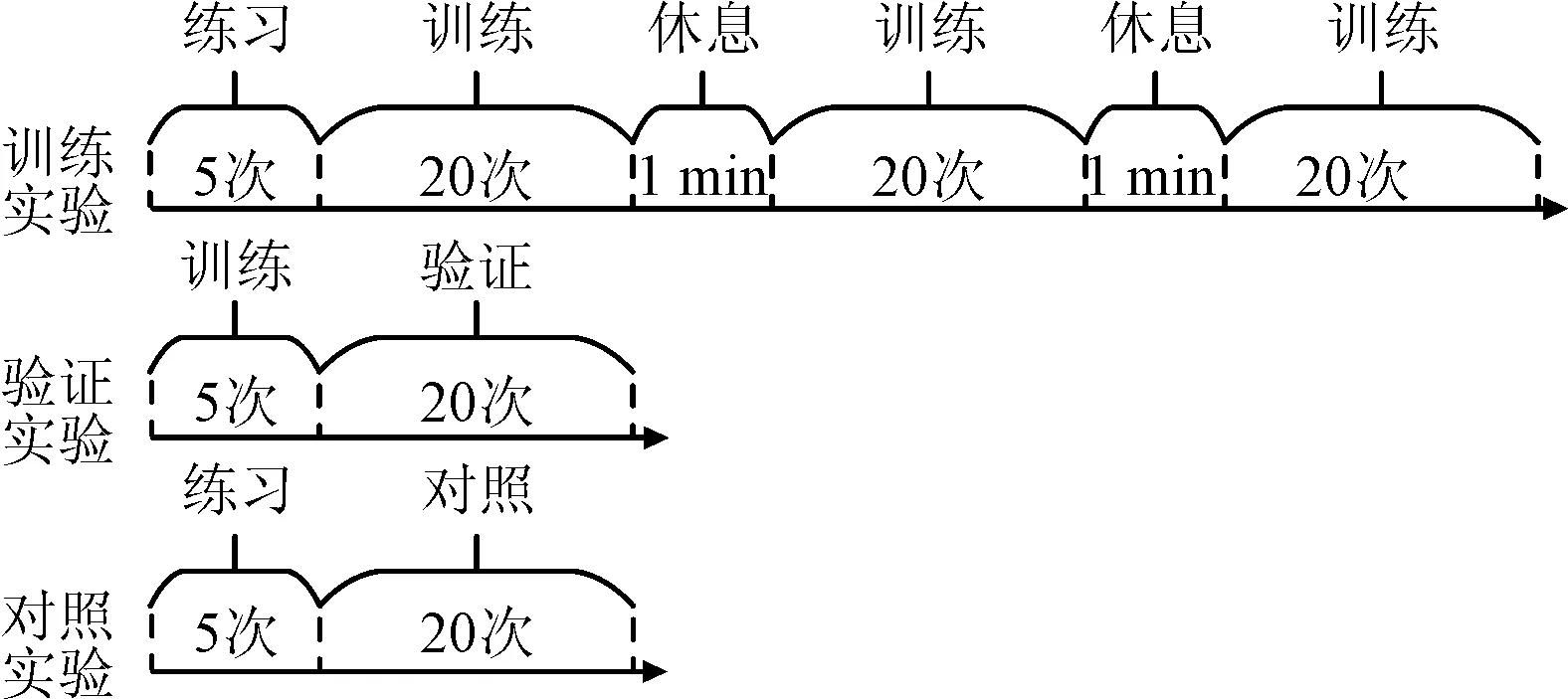
图7 实验步骤示意图

4.3 ADAM优化器学习率分析

通过研究发现ADAM优化器中学习率会影响脑-机协作方法模型的训练效果。分析其原因是由于在模型收敛过程中发生了梯度消失或梯度爆炸的现象。因此为了验证此猜测,这里进行一个离线的测试,选择受试者Sub1的对照组实验数据,以图4中的3层全连接神经网络为基础,建立精神状态影响下的操控品质预测网络,分别设置6种ADAM优化器学习率rL参数,分析学习率与损失函数值之间的关系,具体如图8所示。损失函数值越小,代表神经网络收敛性越好,训练效果越好,反之损失函数值越大,则神经网络收敛性差,训练效果差。当rL≥0.1时,由于梯度爆炸原因使误差曲线出现了二次震荡的现象,并且rL值越大,震荡越剧烈,波峰的横坐标值越大,从而造成收敛速率慢,训练效果差。当rL≤0.01时,由于避免了梯度爆炸而使震荡现象消失。在0.001～0.01之间,rL值越小,初始损失函数值越低,整体收敛效果越好,但是当rL值降低至0.000 1时,由于梯度消失的原因使收敛速率骤然变慢,当迭代50次时,损失函数值是rL=0.001时的15倍,是rL=0.01的28倍;当迭代100次时,损失函数值是rL=0.001时的5.8倍,是rL=0.01时的5倍。实验结果显示:当rL在0.001附近时,既可以避免由于梯度爆炸造成的训练模型鲁棒性差的问题,又可以避免由于梯度消失造成的训练模型收敛过缓的问题,因此可达到最优的训练效果。

图8 学习率与损失函数值间关系

4.4 操控品质分析

为了验证面向精密操控轨迹跟踪任务的脑-机协作方法的有效性,这里主要通过脑-机协作方法模型收敛性和轨迹跟踪任务完成品质两个方面分析。选择具有代表性的受试者Sub1为例进行讨论,该受试者一共进行了8组训练实验,其模型收敛曲线如图9所示,纵坐标为奖励值,代表操控品质。图中置信区间的上限和下限分别为95%。前22次实验曲线呈现剧烈震荡状态,并且置信区间范围较大,说明数据概率分布不稳定。之后模型逐渐稳定,并达到收敛,奖励值稳定在相对较高的1.92水平,其置信区间范围变窄,说明数据概率分布稳定,操控品质维持在相对较高水平。但是,其中仍然存在轻微波动,例如第39和第49次实验的奖励值出现明显的降低,这是因为在训练过程中,脑-机协作方法模型在输出动作指令时按照EEb原则,存在输出非最优速度的概率,会导致受试者的操控品质降低。

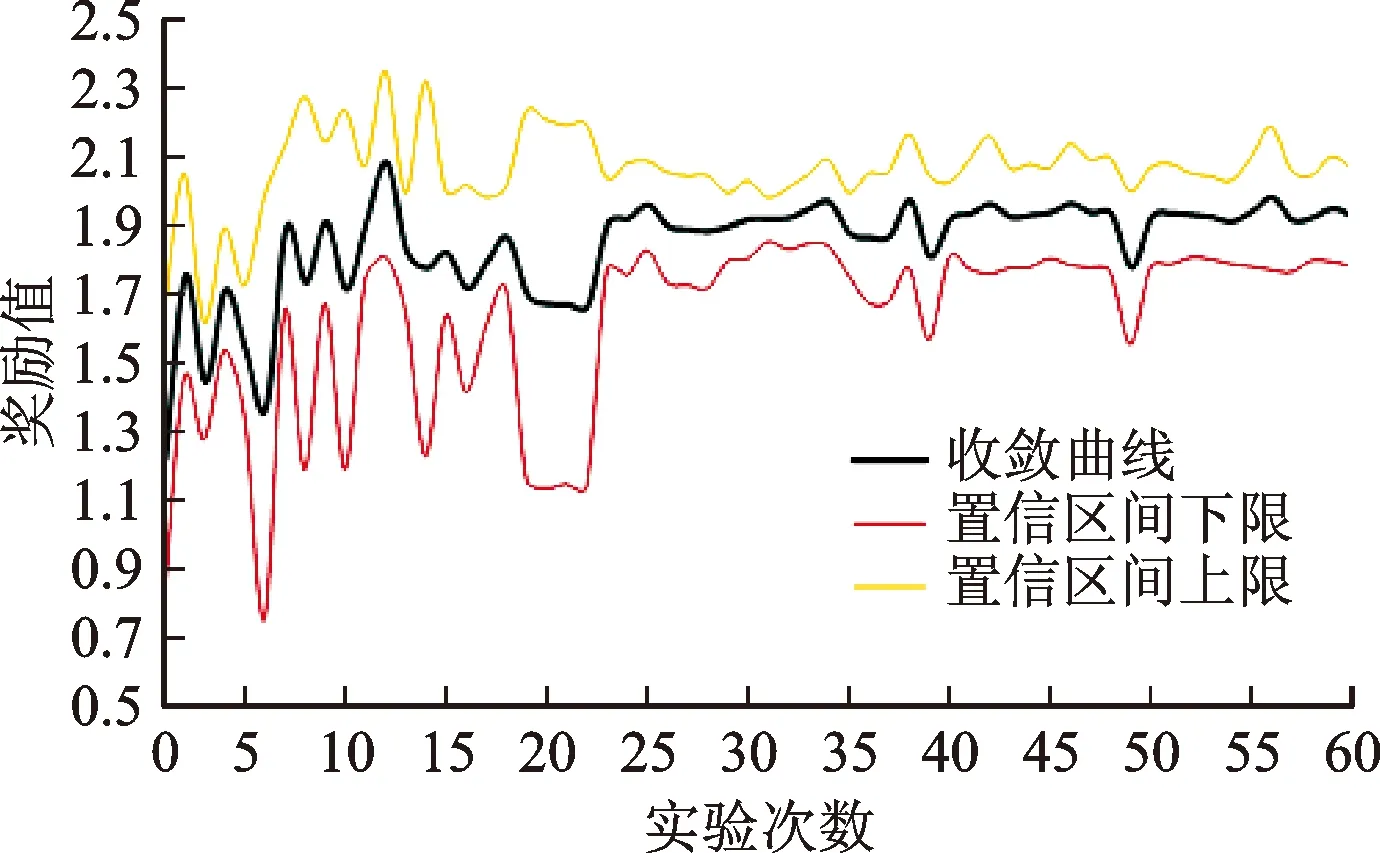
图9 训练模型收敛曲线图

将受试者Sub1训练实验中的脑-机协作方法模型参数导入到验证实验中,对操控品质进行分析,验证实验与对照实验对比曲线如图10所示。由图10可以看到,对照实验曲线在20次实验中剧烈振荡,这是由于对照实验中机器人的速度无法与操控者的精神状态匹配,导致奖励值变化剧烈,且大多数奖励值很低,操控品质很差。相反,验证实验曲线在20次实验中始终保持在一个相对较高的奖励值水平上轻微浮动,说明操控品质良好。原因在于脑-机协作方法可根据操控者的精神状态匹配最优的机器人速度,从而有效提高了操控品质。

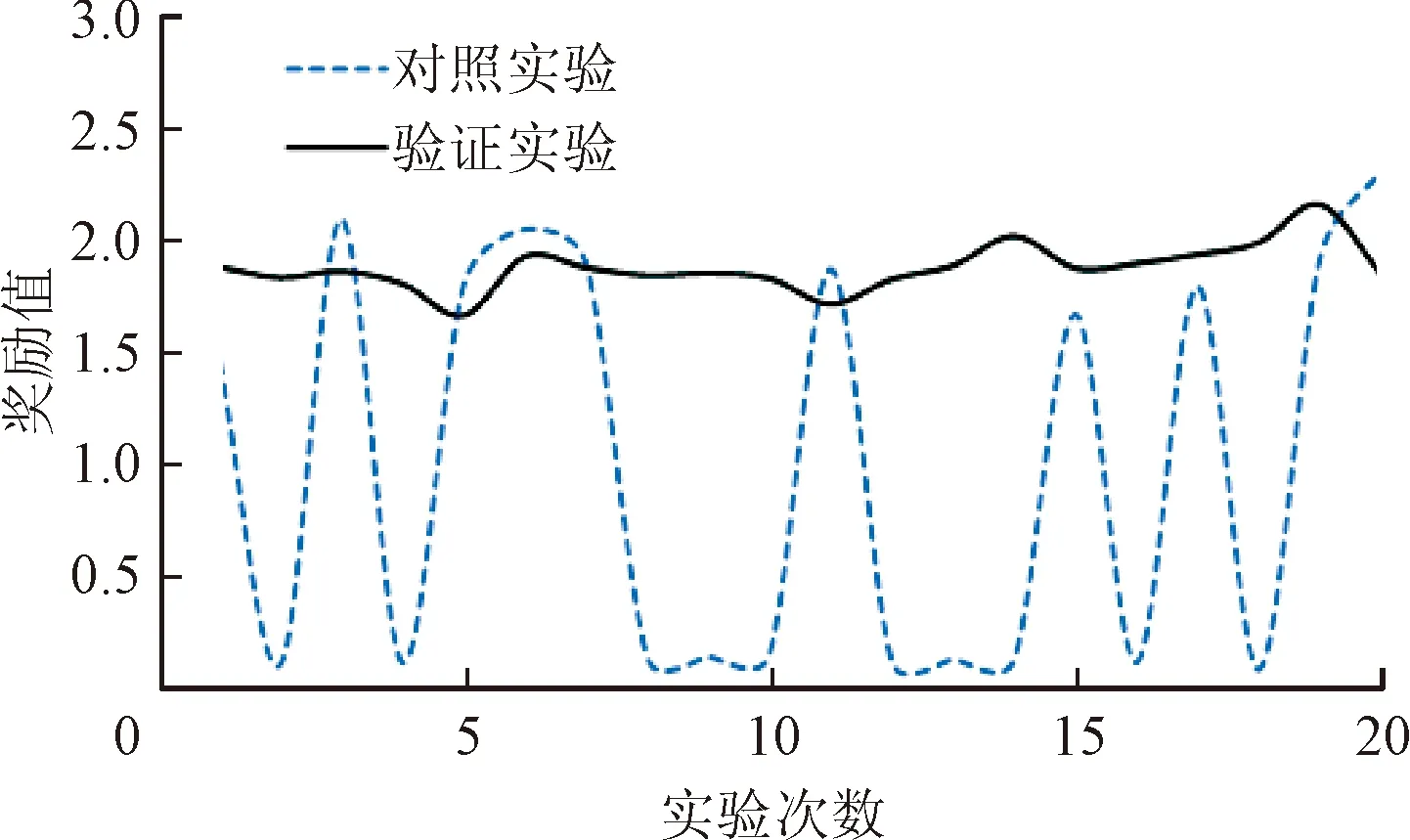
图10 操控品质曲线对比图

为了更直观的讨论脑-机协作方法在轨迹跟踪任务中的有效性,分别记录了受试者Sub1在验证实验和对照实验中的10次轨迹,具体如图11所示。从对照实验相对波动的轨迹上可知,由于其频繁出现目标轨迹缺失现象,从而操控者需要不断地调整方向指令,这不仅导致机器人与障碍物碰撞的次数增加、整个任务所花费的时间变长,而且增加了脑力负荷和负面情绪。而对于使用了该方法的验证实验,其轨迹跟踪精度要优于对照实验,目标轨迹缺失现象较少,不需要操控者频繁调整方向指令,操作更精准和高效。

(a)验证实验结果

为了进一步证明脑-机协作方法的普遍有效性,对所有受试者的操控品质进行了对比分析,结果如表1所示。表1中各指标计算公式如下

(10)

式中:H表示水平直线轨迹的步数;B表示斜线轨迹的步数;C表示曲线轨迹的步数;Rh、Rb、Rc和Rave(为3者之和)分别代表水平直线、斜线、曲线以及整条轨迹的归一化奖励值,其值越大代表轨迹跟踪精度越好,反之,轨迹跟踪精度越差;Rt代表时间指标奖励值,其值越大代表完成时间越短,反之,完成时间越长。因此,Rave+Rt的值越大表示操控品质越好,反之,操控品质越差。表1结果显示:相比较于对照实验,5名受试者验证实验的平均操控品质提高了59.36%,证明了脑-机协作方法的普遍有效性。其中平均轨迹跟踪精度和完成时间两项指标分别提高了36.55%和22.81%,说明此方法不仅提高了轨迹跟踪任务的控制精度,而且缩短了操控的时间。

表1 轨迹跟踪任务操控品质对比表

5 结 论

本文面向人-机交互的精密操控领域,针对人、机之间缺乏信息双向交互,以及操控精度和安全性受操控者精神状态影响的两大问题,通过引入脑-机接口技术,提出了一种脑-机协作精密操控方法研究。通过人机信息交互机制创建、脑-机协作精密操控数学模型推导与算法研究,以及实验验证分析,得出如下主要结论:①结合人在上层规划与机器在精细控制上的各自优势,可以创建一种双环路人-机之间信息交互机制;②通过引入深度强化学习思想,以表征操控者精神状态的EEG微分熵特征作为模型的输入,以机器人速度指令作为模型的输出,可以获得一体化的脑-机协作方法模型;③基于精神状态实时监控,采用3层全连接神经网络感知模型,可以实现脑-机协作精密操控算法;④通过轨迹跟踪虚拟环境和任务场景创建,能够实现对脑-机协作方法的实验验证分析。实验结果表明:本文方法明显提高了轨迹跟踪任务的控制精度,缩短了任务执行时间。本文方法不仅实现了脑-机协作精密操控轨迹跟踪任务,而且借助此项任务的研究,探讨了一体化的脑-机协作模型的构建,促进了脑-机之间的信息双向、实时交互,实现人-机交互系统的互适应、互监督和互增长。