手机APP开发在隧洞测量放样中的应用

刘洋

摘要：本文重点讨论表孔溢洪洞渐变段、上洞身段、渥曲面段、斜井段、下反弧段、下洞身段在施工测量放样中所取得的实践经验，根据表孔溢洪洞施工测量的特点，充分利用现有的测量仪器徕卡全站仪和自主开发手机APP，以手机APP的简单易操作替代传统函数编程计算器，充分结合测量放样与测量APP，在完全保证测量精度的前提下，既保证质量、安全又保证最终测量的点位精度而进行的测量放样方法和数据处理手段。

关键词：全站仪坐标法    测量放样    手机APP

一、表孔溢洪洞工程概况

表孔溢洪洞位于工程区左岸山体中间位置，隧洞全长316.88米，其中最大断面为宽19米×高14米。由控制段闸井经过渐变段、洞身段、渥曲面段、斜井段、下反弧段、洞身段，最后到出口明渠段。隧洞进出口轴线高差为71米，斜井段则布置为与水平夹角为33.67°，城门洞型的设计开挖断面，其渐变段轴线长约47.18米，上洞身段轴线长30.04米，渥曲面段轴线长为42.57米，斜井段轴线长约57.38米，下反弧段轴线长14.07米，下洞身段轴线长139.41米。

二、测量放样方法及其点位的确定

渐变段、渥曲面段、斜井段及其下反弧段的测量放样方法，主要根据施工组织设计按进出口分上下半洞2层对向同步掘进的开挖程序并最终在渥曲面段贯通的要求，分别在进口控制段与出口明渠段布设了施工控制点（支导线网），其相应控制点的三维坐标均由工程首级控制网（复测后）逐级传至布设好的施工控制点上，使其施工控制点最弱点点位误差满足相应水工建筑物测量规范要求。

由于考虑洞内的永久衬砌及钢筋安装，所以在开挖过程中要尽量避免钻爆后无欠挖甚至尽量减小超挖尺寸，以减小不必要的经济损失，则采取将所提供的附近控制点大地坐标经过坐标转换至施工放样所需轴系上的施工坐标系坐标，这样以便更直观地反映在某轴系直平段内不通过计算便可知设计特征点在设计断面上的改正值。

1、测量放样方法和数据处理方法：

根据施工放样所提供的一台LeicaTS-02红外线可见光无棱镜反射全站仪（现场施工技术员用专用反射片作为每一次掌子面放样的测量反射体配合），其全站仪测角精度为2"，测距精度为±（2mm+2ppm×D）。采用直接由离掌子面较近控制点转测站到掌子面附近，用全站仪坐标法测定其测点的坐标值，将全站仪显示屏显示的坐标输入已自主开发并反复验算确保无误的手机测量APP相应的输入框中，进行现场测量数据处理后得出测点与设计点的改正值来确定测点的设计位置。

2、测点精度估算：

采用全站仪坐标法测定其测点的坐标，按<<水利水电工程施工测量规范>>（DL/T5173—2003）的附录H平面位置方法精度估算公式的H.1全站仪坐标法进行测点精度评定，其精度评定结果为测点的点位精度均满足规范要求。

三、测量放样数据处理

测点坐标改正计算主要采用手机测量APP进行所属工程部位编制计算程序并经反复调试而无误后进行现场测量数据输入手机测量APP相应的输入框中处理后得出测点与设计点的改正值。进行设计断面编程计算主要是确定测点在垂直于设计轴中心线的设计标准断面上以设计标准断面上某一特征点为中心所建立的坐标系中的高差值和水平偏离值。

1、开发APP使用工具及软件

使用语言：Delphi

开发工具：Delphi XE10.2

运行平台：Android

数据存储方式：XML本地化存储，因工作环境特殊受到网络限制无法联网处理，所以采用本地化数据库，xml方式存储，为防止离线更改，在app启动时加入效验功能，保证数据准确！

2、实际应用：

2.1、平洞放样

（1）设计思路

洞型为城门洞类型计算方式如下（以伯斯阿木工程表孔溢洪洞为案例）

底板高程=起点底板-（起点与终点底板高程差）/（起点与终点里程差）*（当前里程与起點里程差）;

起拱点高程=底板高程+设计开挖起拱点高;

拱顶中心高程=底板高程+设计开挖洞高;

拱顶任意点高程=底板高程+圆心高程+（ sqrt （ sqr （ 拱顶半径 ） - sqr（ 实测轴距 ） ） ）（备注：sqrt开方函数，sqr平方函数）

（2）软件流程

（3）实际放样案例

2.2反弧段放样

（1）设计思路

洞型为城门洞计算公式（以伯斯阿木工程表孔溢洪洞为案例）

已知反弧半径（圆心到底板）：30.8;

已知反弧角度：31°;

计算当前点与反弧起点角度是否在31°以内来判断当前放样点是否在反弧范围;

底板高程=圆心高程 - sqt（sqr（30.8）- sqr（当前里程 - 圆心里程））;

起拱点高程=圆心高程- sqt（sqr（30.8-起拱点高）-sqr（当前桩号-圆心里程））;

拱顶中心点高程=圆心高程- sqt（sqr（30.8-拱顶中心高）-sqr（当前桩号-圆心里程））;

拱顶任意点高程计算=圆心高程- sqt（sqr（30.8-（隧道圆心高+sqrt（sqr（隧道圆心半径）-sqr（当前轴距 ） ）））-sqr（当前桩号-圆心里程））;

（2）软件流程

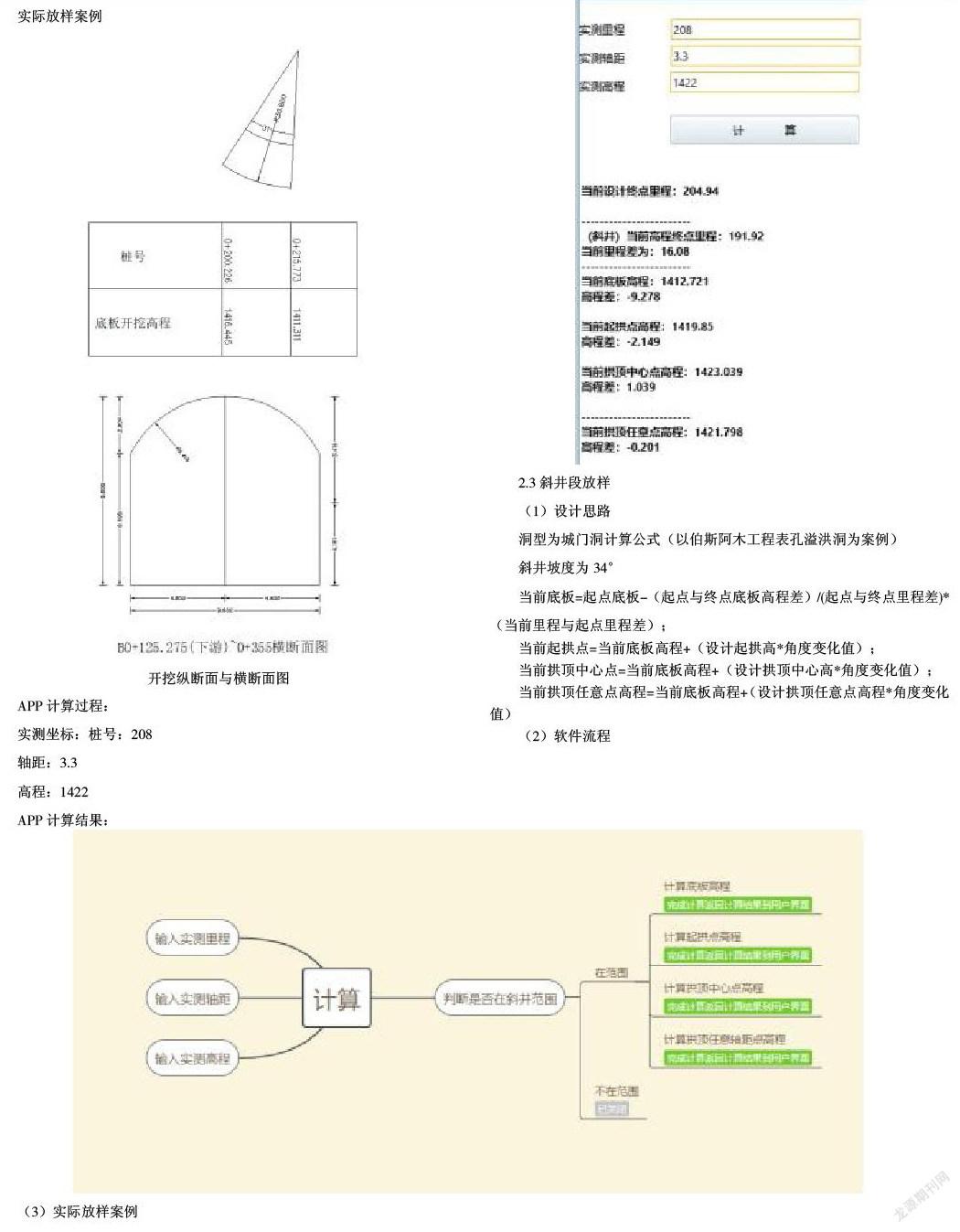
2.3斜井段放样

（1）设计思路

洞型为城门洞计算公式（以伯斯阿木工程表孔溢洪洞为案例）

斜井坡度为34°

当前底板=起点底板-（起点与终点底板高程差）/（起点与终点里程差）*（当前里程与起点里程差）;

当前起拱点=当前底板高程+（设计起拱高*角度变化值）;

当前拱顶中心点=当前底板高程+（设计拱顶中心高*角度变化值）;

当前拱顶任意点高程=当前底板高程+（设计拱顶任意点高程*角度变化值）

（2）软件流程

（3）实际放样案例

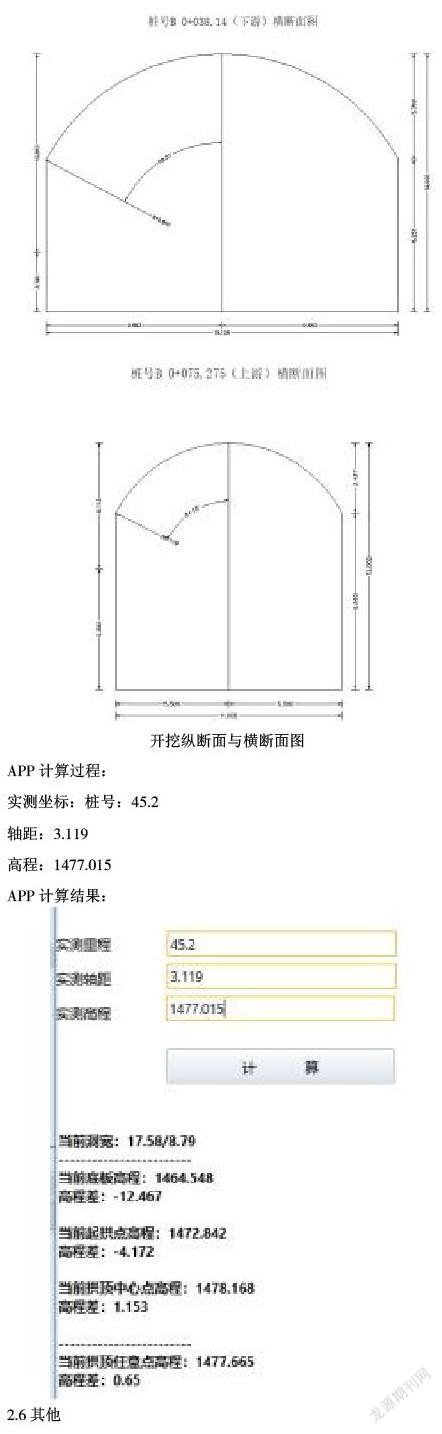
2.4渥曲段放样

（1）设计思路

洞型为城门洞计算公式（以伯斯阿木工程表孔溢洪洞为案例）

渥曲段方程：Y=0.05X+0.00827X^2

底板高程=底板起点高程+0.05*（实测与起点里程差）+0.00827*sqr（实测与起点里程差）;

起拱点高程=起拱点起点高程+0.05*（实测与起拱点起点里程差）+0.00827*sqr（实测与起拱点起点里程差）;

拱顶中心点高程=拱顶中心点起点高程+0.05*（实测与拱顶中心点起点里程差）+0.00827*sqr（实测与拱顶中心点起点里程差）;

拱顶任意点高程=拱顶任意点起点高程+0.05*（实测与拱顶任意点起点里程差）+0.00827*sqr（实测与拱顶任意点起点里程差）;

（2）软件流程

（3）实际放样案例

APP计算过程：

实测坐标：桩号：140

轴距：3.5

高程：1452

APP计算结果：

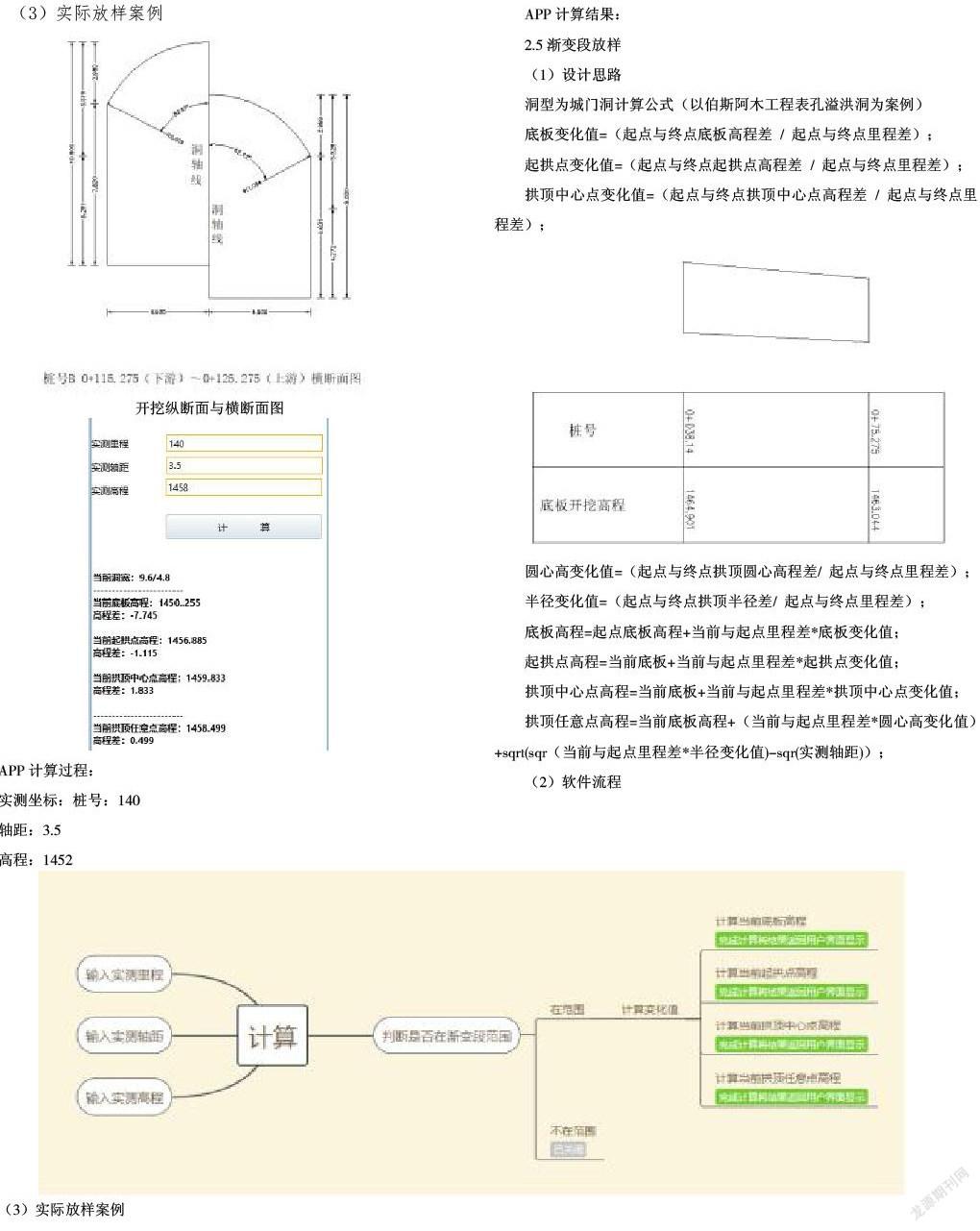
2.5渐变段放样

（1）设计思路

洞型为城门洞计算公式（以伯斯阿木工程表孔溢洪洞为案例）

底板变化值=（起点与终点底板高程差 / 起点与终点里程差）;

起拱点变化值=（起点与终点起拱点高程差 / 起点与终点里程差）;

拱顶中心点变化值=（起点与终点拱顶中心点高程差 / 起点与终点里程差）;

圆心高变化值=（起点与终点拱顶圆心高程差/ 起点与终点里程差）;

半径变化值=（起点与终点拱顶半径差/ 起点与终点里程差）;

底板高程=起点底板高程+当前与起点里程差*底板变化值;

起拱点高程=当前底板+当前与起点里程差*起拱点变化值;

拱顶中心点高程=当前底板+当前与起点里程差*拱顶中心点变化值;

拱顶任意点高程=当前底板高程+（当前与起点里程差*圆心高变化值）+sqrt（sqr（当前与起点里程差*半径变化值）-sqr（实测轴距））;

（2）软件流程

（3）实际放样案例

APP计算过程：

实测坐标：桩号：45.2

轴距：3.119

高程：1477.015

APP计算结果：

2.6其他

（1）自定义函数库

/// <returns>

///  角度转弧度计算函数 AngToRad（角度）：弧度

///</returns>

function AngToRad（Ang： Double）： Double;

/// <returns>

///  弧度转角度计算函数  AngToRad（弧度）： 角度

///</returns>

function RadToAng（Rad： Double）： Double;

/// <returns>

///  正弦函数

///</returns>

function JSin（rad： Double）： Double;

/// <returns>

///  反正弦函數

///</returns>

function RSin（DJSin： Double）： Double;

/// <returns>

///  余弦函数

///</returns>

function JCos（rad： Double）： Double;

/// <returns>

///  反余弦函数

///</returns>

function RCos（DJCos： Double）： Double;

/// <returns>

///  正切函数

///</returns>

function JTan（rad： Double）： Double;

/// <returns>

///  反正切函数

///</returns>

function RTan（DJTan： Double）： Double;

/// <returns>

///  坡比转角度

///  高：距离

///  公式 角度=tab-1*（高差/距离）

///  PitchToAng（高差，距离）：角度

///</returns>

function PitchToAng（height， dist： Double）： Double;

/// <returns>

///  正弦定理：角a/sin对边A=角b/sin对边B=角c/sin对边C

///  限定条件：必须知道2角及其中一角的对边

///  sineRule（角a，对边A，角b，对边B，角c，对边C）;Boolean

///</returns>

function sineRule（out angA， sideA， angB， sideB， angC， sideC： Double）： Boolean;

/// <returns>

///  余弦定理

///  限定条件：已知邊b 边c 角度A

///  公式：a*a=sqr（b）+sqr（c）-2*b*c*cos（A）

///</returns>

function CosB（sideA， sideB， angC： Double）： Double;

/// <returns>

///  保留小数  dec（数值DOUBLE，保留位数INT）：返回处理后数值

///</returns>

function dec（num1： Double; dig： Integer）： Double;

上述APP具体内容及计算程序已在伯斯阿木水库项目表孔溢洪洞隧洞开挖工程测量放样中成功使用，在此列出以供参考。

四、测量放样算例

现场施工测量放样数据则采取现场放样完毕后将所测点号数据存储在全站仪内，回到办公室内将所存储数据传输于计算机上并经内业测量计算人员计算改正数据和桩号数据打印归档。实践证明，其两种计算方法最终的改正数据和桩号数据完全相同，从而说明现场测量放样测点的计算点位坐标改正值是正确的。

五、结束语

众所周知，测量数据的计算处理一直是影响测量进度和测量效益的关键因素之一，本文通过对表孔溢洪洞隧洞渐变段、上洞身段、渥曲面段、斜井段、下反弧段、下洞身段的施工测量放样方法和测量数据的计算和检核方法，并重点讨论了在该类现场施工测量放样方法和测量数据的计算处理和检核方法。通过充分利用手机APP简单易懂，计算精确，方便使用的编程计算，从而给测量人员带来了巨大的方便，对今后在相同类别的工程施工测量中的测量放样方法和测量数据的计算处理提供了借鉴的经验，同时欢迎同行提出更为合理、简单的数据处理的方法和手段。