“数学实验”在数学教学中的实践探索

杨志燕

【摘 要】数学实验注重让学生亲历、体验、感悟、探索，是提升学生数学核心素养的有效载体。数学实验在数学教学中有着非常重要的价值，它可以使教学目标更加聚焦，文本内涵更加丰富，课堂探究更加开放，儿童素养长足提升。

【关键词】数学实验 目标聚焦 文本开发 活动开放 素养提升

所谓数学实验，是指学生根据教师创设的情境或问题，进行观察、操作、探究等一系列思维活动，对得出的数学结论进行检验，对已有的数学事实进行猜想并探究的过程。

数学实验作为数学有效学习的载体，从学生已有的经验出发，让学生亲历实验的过程，更加注重学生体验、猜想、验证的过程，能有效调动学生的主观能动性，促进学生深度思考，帮助学生对数学知识的理解和掌握。数学实验过程中，学生做中玩、做中学，凸显了学生的主体地位，同时大大增加了数学的趣味性，学生获得了成功的体验。数学实验在数学教学中的价值不言而喻，如何让数学实验在小学阶段有效开展，笔者在自己的教学中开展了一些实践探索。

一、目标聚焦：让目标视角从“迷糊”走向“清晰”

数学实验在当前的数学教学中也存在一些误区：有的教师为了追求实验的趣味性，没有搞明白实验的真正目的，为了实验而实验，把实验课上成了活动课，课堂表面看上去热闹，实际意义却不大，浪费了课堂上大量宝贵的时间。教师必须明确实验的目的是充分调动学生探究的积极性。小学生年龄小，缺少生活经验，有些知识比较抽象，学习起来感到吃力。做一遍往往比看一遍更容易理解和印象深刻。

数学实验：测量土豆的体积

在学习完圆柱和圆锥的体积计算之后，学生会用公式完成圆柱和圆锥的体积计算了。这时，教师拿出一个土豆，让学生测量土豆的体积。土豆是不规则物体，是不好直接测量的。学生会产生疑问，这时教师可以提供一些实验的工具，鼓励学生想办法测量出土豆的体积。学生的兴趣被激发，自然更乐意去探究。

实验教学预案：

实验主题：

测量土豆的体积。

实验目标：

1.让学生想办法测量土豆的体积，经历猜想、观察、验证和概述的过程，进一步感受分析问题和解决问题的意义。

2.使学生在实践探究的过程中，体会研究问题的一般方法，培养认真严谨的态度。

3.使学生在实验中进一步感受数学与生活的紧密联系，提升灵活运用数学知识解决生活中问题的意识和能力。

实验材料：

一个土豆;一个圆柱体（或长方体、正方体）容器;一些水和刻度尺。

实验过程：

1.在规则容器中装入一些水，测量水位高度。

2.把土豆浸没在水中，再次测量水位高度。

3.想办法测量出土豆的体积。

4.得出实验结论。

实验反思和结论：

（学生实验后填写）

教师创设了测量土豆的体积这个数学实验。教学中很多教师会把这个实验忽略，认为没必要让学生去做，浪费时间，讲一讲学生就能懂。笔者认为不是这样的，教师从学生的生活实际出发，把教學内容和生活实践紧密联系，让学生学以致用，激发了其主动探究的兴趣，使学生感受到数学的魅力，学会用所学知识解决问题。看起来复杂的问题被学生轻易解决，学生增强了其学习数学的自信心，同时也明白了不规则物体的体积可以通过转化求得，为后面学习转化的策略做了很好的铺垫。

二、文本开发：让文本视角从“单一”走向“多元”

苏教版数学教材比较注重学生动手实践能力的培养，但是教材毕竟是教材，能提供给学生的学习内容是相对固化的。教师可以借助数学实验，让学生在探索文本内容的过程中适时捕捉机会，举一反三，拓展思维;沟通知识间的联系，进一步丰富文本教材的内涵。

数学实验：圆柱体积的推导

学生已经有了计算长方体和正方体体积的经验，再来学习圆柱的体积时，笔者放手让学生合作探究，学生把圆柱沿着底面半径和高切成若干等份拼成长方体。

在动手实践的过程中，学生理解了圆柱的体积等于拼成的长方体的体积，长方体的底面积等于圆柱的底面积，长方体的高等于圆柱的高，得出“圆柱的体积等于底面积乘高”的关系，即S=（πr） ·r·h=πr2 h。

教师接着提问：如果把拼成的长方体的前面或右侧面作为长方体的底面，还能推导出圆柱的体积计算公式吗？

实验教学预案：

实验主题：

圆柱体积的计算公式还有不一样的推导方法吗？

实验目标：

1.通过教材内容的启发，提出疑问，自主探索用不同的方法推导出圆柱的体积计算公式。

2.在观察、猜想、验证的活动过程中，感受方法的多样性和关联性，提升学生的数学思维能力。

3.借助实验探究，增强学习数学的兴趣，感受数学的魅力。

实验材料：

沿着底面半径和高分成若干等份的圆柱模型。

实验过程：

通过拼、摆等方法，推导出圆柱的体积计算方法。

实验反思和结论：

（学生实验后填写）

学生探究后得出：拼成的长方体前面作底面，底面积就是（πr）·h，高就是r，长方体体积S=（πr）·h·r，化简得出S=πr2 h。同理拼成的长方体的右侧面作为底面，底面积就是（rh），高就是πr，长方体体积S=（r h）·（πr），化简得出S=πr2h 。学生通过探索圆柱体积的推导方法，虽然方法上略有不同，但不管用哪个面作为长方体的底面，都能推导出圆柱的体积公式，三种方法相互印证，可以很好地加深学生对圆柱体积公式的理解。

实验中教师借助数学实验对文本进行了二次开发，让学生经历了再探究、再思考的过程，不仅验证了圆柱体积计算公式，还沟通了知识间的联系，加深了对公式的理解，比教师的“讲解”更具说服力和深刻性。

三、活动开放：让学情视角从“会动手”走向“真探究”

有些教师思想上不够重视，认为数学实验往往要花费很长时间，最后也就是得出了书上的“结论”。这些教师的课堂上往往出现这样一种现象：教师拿着教具或对着课件投入地讲解着数学实验，而不给学生“做实验”的机会，但学生似乎对实验结果也掌握得不错。难道这些数学实验真的可以不做吗？“做实验”真的是在浪费时间吗？其实，实验就是让学生经历观察、猜测、推理、验证等环节，在每一个环节中学生都会有自己的理解，实验可以促进他们学会用数学的眼光思考问题，用数学的方法探索问题。

数学实验：大树有多高

实验教学预案：

实验主题：

大树有多高。

实验目标：

1.通过测量各种物体影子长度的实践活动，探索影子长度与物体实际高度之间的比例关系。

2.通过分组合作，培养学生动手动脑、解决实际问题的能力和团结协作精神。

3.借助实验活动，感受数学与生活的紧密联系，进一步激发数学学习的兴趣，并在活动中培养创新精神。

实验材料：

竹竿、卷尺。

实验过程：

1.找几根同样长的竹竿直立在地面上，并量出每根竹竿的影长。

2.把几根不同长度的竹竿直立在地面上，量出每根竹竿的影长，并算出比值。

3.同时量出一根竹竿和一棵大树的影长，再量出竹竿的长度。

实验反思和结论：

（学生实验后填写）

实验步骤确定了之后，学生按照步骤进行操作，在实验过程中也能如实记录，并收集整理数据，这是我们所说的“会动手”。但是学生在实验中经常会碰到一些小问题，教师要鼓励学生寻找解决问题的策略。学生解决不了的，教师要及时记录，对实验中普遍存在的问题进行分析，鼓励学生在实验过程中积极参与思考，用自己的数学思维方式分析问题和解决问题。因此，教师在课堂教学中要根据教材的需要，经常设计一些开放性的实验活动，引发学生的数学思考，让学生真正从“会动手”走向“真探究”。

四、素养提升：让儿童视角从“眼下”到“长远”

南开大学顾沛教授说：“数学素养就是把所学的数学知识忘掉后剩下的东西。”学生在课堂上学到的知识随着时间的推移很多都会忘记，但是用数学的眼光看待问题、用数学的逻辑思考问题、用数学的理性解决问题等，这些才是学生宝贵的精神财富，是学生受用终身的数学素养。

数学实验：怎样滚得远

实验教学预案：

实验主题：

当斜坡与地面成什么角度时，物体滚得远一些呢？

实验目标：

1.让学生自主探索斜坡与地面成什么角度时，物体滚得远一些。

2.在观察、猜想、验证的活动过程中，发现当斜坡与地面成45°时，物体滚得远。

3.借助实验研究，增强学习数学的兴趣和信心。

实验材料：

木板、圆柱形物体、尺子。

实验过程：

步骤1：用木板搭一个与地面成30°的斜坡。

步骤2：将圆柱形物体放在斜坡的顶上。

步骤3：轻轻松开手，让物体自动往下滚。

步骤4：等物体停止滚动后，量出它在地面上滚动的距离。

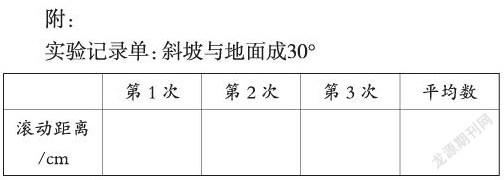
反复做几次这样的实验，测量并记录每次滚动的距离，再求出它们的平均值。

把木板分别搭成与地面成45°和60°斜坡，進行同样的实验，并记录实验的结果。

实验反思和结论：

（学生实验后填写）

有些教师片面地认为，只要让学生记住结论即可。其实实验的目的，不仅仅是知道斜坡与地面成45°时物体滚得远，更重要的是实验中的分工合作，有序思考，对出现的问题能有效解决等。实验是面向每一个儿童的，儿童在实验中各方面都能有所发展才是我们最终的目的。