基于混沌理论的混凝土裂缝开合度改进混合预测模型

2021-02-14徐小枫黄耀英何一洋

水资源与水工程学报 2021年6期

徐小枫，黄耀英，徐耀，何一洋，颜剑

(1.三峡大学水利与环境学院，湖北宜昌 443002； 2.中国水利水电科学研究院材料研究所，北京 100038； 3.湖北汉江王甫洲水力发电有限责任公司，湖北襄阳 430048)

1 研究背景

裂缝是水工混凝土结构常见病害之一。对于带宏观裂缝运行的水工混凝土结构，裂缝的工作性态直接关系到整个结构的安全状况，是判定结构稳定性的一个重要指标。为了掌握混凝土裂缝的工作性态，工程上常通过安装裂缝计组对裂缝的开合度和错动量进行实时监测。由于工程现场条件复杂，实际混凝土裂缝会受到水压、温度和时效等多种因素的综合影响。因此，建立准确的混凝土裂缝开合度数学监控模型，对裂缝开合度性态进行定量分析评价和预测具有重要的意义。

目前，基于传统混凝土变形统计模型[1]所建立的数学监控模型被广泛应用于变形预测[2]、参数反演[3]等工作中。其模型形式通常包含了温度分量、水压分量和时效分量等。然而，由于传统统计模型一般只考虑温度的线性影响而忽略了实际效应量与环境因子之间复杂的非线性关系，导致温度分量存在欠拟合的问题[4-5]。研究表明，温度荷载是使大体积混凝土产生裂缝的主要驱动力[6-7]，混凝土裂缝的形成和扩展对温度变化十分敏感[1]。然而，关于考虑温度非线性影响的混凝土裂缝开合度统计模型的研究很少。此外，近年来，为进一步对统计模型的预测性能进行改进，相关学者探索了利用混沌理论对统计模型的残差序列进行分析预测的方法[8-10]，并认为残差时间序列含有混沌特性，从而通过建立混合模型来改善统计模型的预测效果。其中文献[8]将混沌理论应用到混凝土裂缝开合度预测中，取得了良好的预测效果。

基于混沌理论的残差序列预测方法是在Takens嵌入定理[11]的基础上，确定最佳延迟时间与最小嵌入维数，从而将一维时间序列重构为与原动力系统具有相同拓扑意义的多维相空间，进而利用其内部非线性映射关系，将一维时间序列的外延转为多维相空间的内插，并结合Lyapunov指数的性质，便可实现对混沌时间序列的识别和短期预测[9,12]。目前，有关最佳延迟时间计算方法的研究表明，平均位移法[13](average displacement method，简称AD法)在计算最佳延迟时间时，克服了自相关系数法[14]的主观性和其对非线性系统的不适用性[15]以及互信息法[16]计算时的繁杂性等，且能有效避免延迟时间取值不当导致的信息冗余或延迟坐标的完全不相关。Cao法[17]在计算最小嵌入维数时，改善了几何不变量法[11]的不抗噪性以及虚假邻近点法[18]的主观性。此外，AD法和Cao法均能适应较小的数据集。目前，应用AD法和Cao法对混凝土结构位移统计模型的残差序列进行相空间重构收到了良好成效，但在混凝土裂缝开合度方面的应用却鲜有文献报道，且组合应用AD法与Cao法来重构相空间的报道也较少。近年来，随着人工神经网络的发展，针对基于人工神经网络确定非线性映射关系的方法也得到了发展应用[19-21]。研究表明[20-21]，BP(back propagation)神经网络具有较强的非线性映射能力与自适应学习能力，在混沌时间序列的预测中表现出良好的适应性与稳定性，但单一的神经网络存在收敛速度慢，容易陷于局部极小值和过拟合等不足[21]，Ding等[22]的研究表明遗传算法(genetic algorithm, GA)对BP神经网络有明显的改善。因此，相空间重构理论结合GA-BP神经网络可实现混沌残差时间序列较为有效的预测[21]。

本文为提高混凝土裂缝开合度预测精度，首先对传统统计模型的温度分量形式进行改进，然后在混沌理论基础上，对残差时间序列进行相空间重构，建立GA-BP神经网络对残差进行预测，最终建立改进混合预测模型对混凝土裂缝开合度进行预测。

2 模型建立

2.1 混凝土裂缝开合度改进统计模型

根据文献[1]建立裂缝开合度统计模型(简称传统统计模型)为：

δ(t)=δT(t)+δH(t)+δθ(t)+δε(t)

(1)

式中：δ(t)为裂缝开合度实测值，mm；δT(t)、δH(t)和δθ(t)分别为温度分量、水压分量和时效分量，mm；δε(t)为残差，mm；Ti为第i个测点实测温度，℃；K为温度测点总数；H为水深，m；θ=t/100，t为时间，d；a0，ai，bi，c1，c2均为回归系数。

基于变形统计模型的相关研究[2,8-9,21]，通常情况下只考虑了温度的线性影响，而研究表明[4]，公式(1)中的温度分量表达式没有考虑温度非线性因素影响，忽略了环境量的复杂性，将会出现欠拟合现象。为此，文献[5]考虑温度滞后效应，并建立了考虑温度非线性影响的位移统计模型，但其形式复杂，实现过程较为繁冗。因此，针对混凝土开合度随温度变化的非线性过程，综合考虑温度非线性影响与模型的简洁性，建立混凝土开合度的改进温度分量统计模型(简称改进统计模型)为：

δ(t)=δT(t)+δH(t)+δθ(t)+δε(t)=a0+

(2)

式中：L为反映非线性温度影响的温度多项式的最高阶次，通常为正整数，通过试算确定；aip为第i个测点实测温度的p次方对应的回归系数；其余符号含义同前。

2.2 残差时间序列预测模型

2.2.1 残差时间序列相空间重构研究表明[8,11]，对于一维残差时间序列x(t)={x(ti)|i=1,2,…,N}，可以将其重构为如下形式的m维相空间：

X(ti)=[x(ti),x(ti+τ),…,x(ti+(m-1)τ)]T

(i=1,2,…,M)

(3)

式中：M为相点数，M=N-(m-1)τ；m为嵌入维数，取正整数；τ为延迟时间。

由公式(3)可知，相空间重构的关键在于延迟时间τ和嵌入维数m的确定，其计算方法分述如下。

(1)延迟时间的计算。

采用AD法[13]计算延迟时间。在2-范数下定义平均位移S2(m,τ)为：

(4)

当给定不同的嵌入维数m(m≥2)时，S2(m,τ)会随τ的增加而趋于稳定。为此，文献[13]建议最佳延迟时间可以根据不同嵌入维数m下的S2(m,τ)-τ图形来确定，即当S2(m,τ)-τ斜率衰减为初始斜率的40%时，对应的τ0为最佳延迟时间。

(2)嵌入维数的计算。采用Cao法[17]计算嵌入维数。当给定一个最佳延迟时间后，在m维相空间中定义如下几个参数。

定义参数a(i,m)为：

(5)

Xi(m)=[x(ti),x(ti+τ),…,x(ti+(m-1)τ)]T

(i=1,2,…,N-(m-1)τ)

(6)

式中：‖Xi(m)-Xn(i,m)(m)‖∞为无穷范数下定义的距离；Xn(i,m)(m)为相点Xi(m)的最邻近点[18](下标n(i,m)表示最邻近点)。

a(i,m)的均值E(m)定义为：

(7)

当嵌入维数由m升到m+1时，定义E1(m)为：

(8)

文献[17]的研究表明，如果残差时间序列存在定点吸引子，当嵌入维数m大于某一个m0时，E1(m)将停止变化，此时，m0+1即为最小嵌入维数me，其可由E1(m)-m图形分析确定。

在实际计算中，很难判断E1(m)是缓慢增长还是随着m的增长而停止变化。对于一组随机的残差序列，E1(m)原则上会随着m的增加而不断增加；对于确定性残差序列，E1(m)一定能收敛。因此，有必要引入另外一个参数E2(m)来区分随机残差序列与确定性残差序列，E2(m)定义如下：

(9)

(10)

对于随机残差序列，E2(m)对于任何m均等于1；对于确定性残差序列，E2(m)与m相关，一定存在一些m使得E2(m)≠1。为此，文献[17]建议同时计算E1(m)和E2(m)来确定最小嵌入维数以及区分随机残差序列和确定性残差序列。为方便表述，以下分别用E1、E2表示E1(m)、E2(m)。

2.2.2 Lyapunov指数最大Lyapunov指数λ1对于混沌特性的判断具有十分重要的意义[9,12]，对于一个时间序列，当λ1大于0时，认为该系统存在混沌特性。同时，最大Lyapunov指数的倒数λ1-1定义了最大预测步长[12]，可以作为短期预报的可靠性指标[23]。本文运用Rosenstein法[24-25]计算最大Lyapunov指数。

2.2.3 GA-BP神经网络预测残差

(1)基于混沌理论的非线性预测原理。文献[8]指出，在残差时间序列重构的相空间中，存在唯一的映射关系有：

X(t+Pt)=F(X(t))

(11)

式中：Pt为预测时间，映射关系F可由相空间中的所有相点逼近求得。本文采用GA-BP神经网络进行全域法近似构造该非线性映射关系[20]。

(2)GA-BP神经网络。魏博文等[21]的研究表明，BP神经网络在求解非线性映射关系时具有一定的优势，同时利用遗传算法建立的GA-BP神经网络对典型的混沌时间序列具有较好的非线性拟合能力和更高的短时预测准确性，预测性能优于BP神经网络。为此，本文将采用遗传算法对BP神经网络进行优化，建立GA-BP神经网络进行预测，并在关于遗传算法相关应用研究的基础上[21-22]，参考Xu等[26]的研究，选择如下形式的适应度函数：

(12)

公式(11)综合考虑拟合误差与拟合优度两个重要的评价标准，当R2越大、RMSE越小时，则适应度越大，当适应度不再随进化代数发生变化时，即得到最优适应度。其中，R2和RMSE的计算公式如下：

(13)

(14)

在GA-BP神经网络中，输入向量和输出向量分别为：

X(t)=[x(t),x(t-τ),…,x(t-(m-1)τ]T

(15)

X(t+Pt)=[x(t+Pt),x(t+Pt-τ),…,x(t+

Pt-(m-1)τ)]T

(16)

由分离出的残差时间序列进行神经网络模型优化训练，获得GA-BP神经网络模型的权值和阈值，进而进行残差时间序列的预测。

2.3 裂缝开合度改进混合预测模型

集成裂缝开合度改进统计模型公式(2)与GA-BP神经网络残差预测结果公式(16)，得到裂缝开合度改进混合预测模型(简称改进混合模型)为：

δ(t+Pt)=δT(t+Pt)+δH(t+Pt)+

δθ(t+Pt)+x(t+Pt)

(17)

式中：δT(t+Pt)、δH(t+Pt)和δθ(t+Pt)分别为预测时间为Pt的温度分量、水压分量和时效分量，mm；x(t+Pt)为GA-BP神经网络残差预测模型的预测值，mm。

建立裂缝开合度改进混合预测模型的流程图如图1所示。

3 实例分析

3.1 工程概况

王甫洲水利枢纽位于湖北省老河口市近郊的汉江干流上，是一座以发电为主，结合航运，兼有灌溉、养殖、旅游等综合利用的大(2)型水利枢纽工程。枢纽由位于主河道的泄水闸、主河床土石坝、谷城段土石坝及位于老河道的电站厂房、船闸、混凝土重力坝和两岸围堤土石坝组成。现场巡视检查发现，泄水闸左岸门库上游交通桥顶部出现3条裂缝对门库挡水形成威胁。为了对泄水闸检修门库的裂缝进行工作性态诊断，安装了9套振弦式双向裂缝计组(记作Mkj-1～Mkj-9)进行监测，如图2所示。其中，Mkj-1、Mkj-2安装在门库上游侧面；Mkj-3、Mkj-4、Mkj-5安装在门库顶靠近上游面；Mkj-6、Mkj-7安装在门库内靠近上游面；Mkj-8、Mkj-9安装在门库顶靠近下游面。于2020年6月12-19日，对9套双向裂缝计进行了安装调试。选择典型裂缝计Mkj-3作为分析对象。

图1 裂缝开合度改进混合预测模型建立流程图

图2 实例工程双向裂缝计布置示意图

2020年6月23日至2021年2月14日典型裂缝计Mkj-3实测开合度及温度过程线如图3所示。

图3 裂缝计Mkj-3实测裂缝开合度及温度过程线

由图3可见，泄水闸门库裂缝开合度与温度变化呈明显的负相关，温度升高时，裂缝闭合，温度降低时，裂缝张开。以下结合该裂缝计实测裂缝开合度建立裂缝开合度改进混合预测模型，然后进行分析评价。

3.2 泄水闸裂缝开合度改进统计模型的建立

3.2.1 改进统计模型参数L的确定不同测点受温度非线性的影响可能存在差异，为了合理确定改进统计模型公式(2)中的参数L，考虑9套裂缝计温度测值，对参数L的取值进行试算分析，分别建立L=1、2、3、4、5的裂缝开合度改进统计模型，然后进行回归分析，获得不同L取值对应的模型回归系数，进而计算得到不同改进模型对应的R2和RMSE，如图4所示。

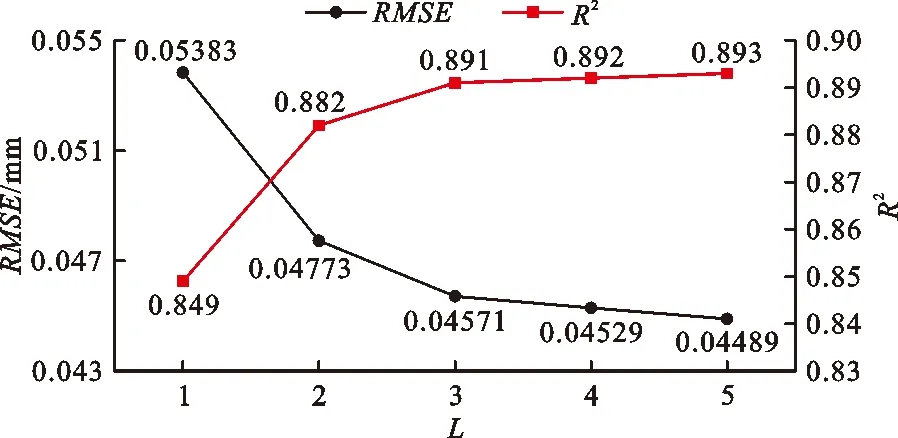
图4 改进统计模型R2、RMSE值随L的变化曲线

由图4可见，当L从1增加到3时，改进统计模型的两个评价参数得到较明显的改善；当L≥3时，两个评价参数逐渐趋于稳定。说明从统计模型的角度上看，温度对混凝土开合度的非线性影响是存在的。由此建立L=3时考虑温度非线性的改进统计模型，如公式(18)所示，此时R2=0.891，RMSE=0.045 71 mm。通过回归分析得到的公式(18)各回归系数值如表1所示。

c2lnθ+δε(t)

(18)

式中各符号含义同前。

3.2.2 裂缝开合度改进统计模型分析 2020年6月23日至2021年2月14日裂缝开合度改进统计模型(公式(18))与传统统计模型(公式(1))拟合结果如图5所示。

分析图5可知：(1)传统统计模型只考虑了温度的线性影响，在极值附近的点拟合效果并不理想，如图5(a)中椭圆圈所示；(2)改进统计模型考虑了温度的非线性影响，拟合效果得到了改善，如图5(b)中椭圆圈所示，拟合曲线更接近于实测值，改进统计模型的残差也更接近于0(图5(c))；(3)由于统计模型本身的局限性，改进统计模型在某些时段仍然存在拟合不佳的状况(图5(b)、5(c))，这将在一定程度上影响预测效果，因而基于统计模型的预测方法仍有改进的空间。为此，进一步利用混沌理论对残差进行分析，建立改进混合预测模型以改善预测效果。

表1 裂缝开合度改进统计模型公式(18)各回归系数值

3.3 残差时间序列预测

(1)嵌入维数和延迟时间确定。本文通过计算不同嵌入维数下的最佳延迟时间以及计算最佳延迟时间对应的嵌入维数来相互印证，并最终确定最佳延迟时间与最小嵌入维数。在裂缝开合度改进统计模型的基础上，由实测值分离获得残差时间序列，从残差时间序列中选取2020年6月23日22：00至2021年2月11日7：00的1 825个样本作为重构数据集。依据平均位移法绘制嵌入维数分别为2、5、8、12时的S2(m,τ)与延迟时间τ的关系曲线，最终根据Cao法绘制E1、E2与嵌入维数m的关系曲线，如图6、7所示。

由图6、7可见：(1)当嵌入维数一定时，S2(m,τ)-τ的斜率随着τ的增大而逐渐趋于稳定，当S2(m,τ)-τ的斜率衰减为初始斜率的40%时，认为此时的τ是最佳延迟时间，由此得到最佳延迟时间为2；(2)在给定的最佳延迟时间下，E2并不是恒为1，且E1随着嵌入维数的逐渐增大而渐趋稳定，由此获得E1值趋于稳定时对应的嵌入维数，即最小嵌入维数为8。根据公式(3)对残差时间序列进行相空间重构。

(2)预报步长的确定。运用Rosenstein法计算得到最大Lyapunov指数λ1=0.025>0，这表明系统存在混沌成分，进而计算其倒数，得到最大预报步长为40。为此，本文取后验步长为24(即2021年2月11日10：00-2021年2月14日7：00的24个样本)，时长为3 d。

(3)GA-BP神经网络预测残差。根据前文2.2.3节中所述原理，采用GA-BP神经网络对2020年6月23日22：00-2021年2月11日7：00的1 825个样本建立的重构相空间矩阵进行优化训练。其中BP神经网络结构为8-12-8，遗传算法最大进化次数为30次，种群数量为40，交叉概率为0.80，变异概率为0.10，适应度随进化代数变化曲线如图8所示。

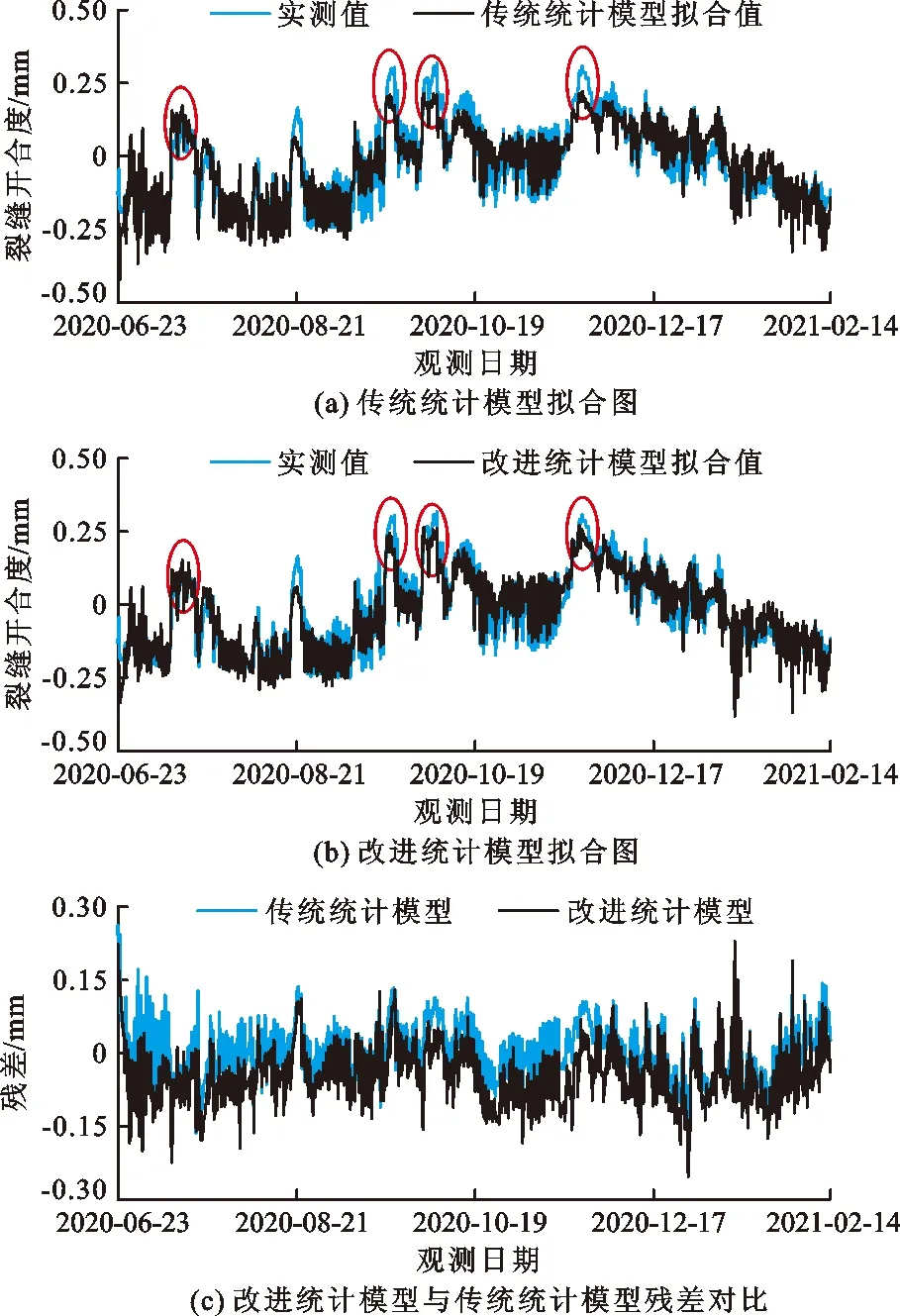
图5 裂缝开合度改进统计模型与传统统计模型拟合结果对比

图6 不同嵌入维数的S2(m,τ)-τ关系曲线图7 E1、E2与嵌入维数m的关系曲线

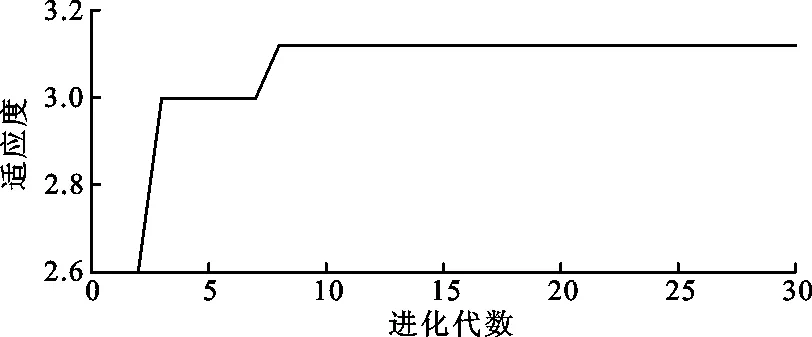
图8 适应度随进化代数变化曲线

由图8可见，当适应度不再明显变化且满足神经网络精度要求时，用此时输出的权值、阈值参数建立优化后的BP神经网络，对重构后的残差时间序列进行训练预测。根据建立的GA-BP神经网络残差预测模型，分离获得残差时间序列的预测值为x(t+1)，x(t+2)，…，x(t+24)。

3.4 改进混合预测模型与预测结果评价

(1)建立改进混合预测模型。由公式(18)集成得到改进混合预测模型为：

c2lnθ+x(t+Pt)

(19)

式中：δ(t+Pt)为预测时间为Pt的裂缝开合度预测值，mm，其中Pt=1，2，…，24。

(2)预测效果评价。引入均方误差MSE、平均绝对误差MAE和归一化误差NRMSE对改进混合预测模型预测效果进行评价，这3个评价指标的值越接近于0，说明预测效果越好，其计算式如下：

(20)

(21)

(22)

式中：σ为实测值标准差，其余符号含义同前。

由公式(19)得到改进混合预测模型从2021年2月11日10:00开始，预测步长为24(即3 d)的预测值，并与传统统计模型及改进统计模型的预测结果进行对比，如图9所示。

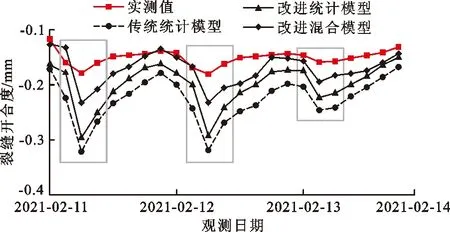
图9 不同模型对裂缝开合度的预测值与实测值过程线

不同预测模型对应的评价指标计算结果见表2。

表2 不同模型对应的各评价指标计算结果及比较

由图9可见，相对传统统计模型的预测值来说，考虑温度非线性因素影响的改进统计模型预测值与实测值更接近，但在极值点附近，改善效果不明显；相对改进统计模型的预测值来说，改进混合模型预测值与实测值吻合效果更好，且在极值点附近的预测值与实测值的差值也明显减小。由表2可见，相对传统统计模型来说，改进统计模型的MSE、MAE和NRMSE值分别减小了51.1%、35.3%、30.0%，改进混合模型的MSE、MAE和NRMSE值分别减小了87.0%、68.5%、63.9%；相对改进统计模型来说，改进混合模型的MSE、MAE和NRMSE值分别减小了73.4%、51.4%、48.4%。结果表明，基于相空间重构理论与混沌理论的改进混合模型可明显改善预测效果。

3.5 裂缝开合度动态预测分析

实际工程中预测预警是一个动态过程，随着时间推移，裂缝开合度不断演变，当获得新的监测数据后，需要重新确定预测模型的参数，进而进行动态预测。为此，为验证改进混合预测模型的可靠性，连续动态预测10次，每次预测的时间步长均为24(即3 d)，进而分别对传统统计模型、改进统计模型和改进混合模型的MSE、MAE和NRMSE进行统计分析。对于这3个指标采用与表2相同的方法，分别计算改进混合模型相对于传统统计模型和改进统计模型的提升率，并绘制箱线图进行对比分析，如图10所示。

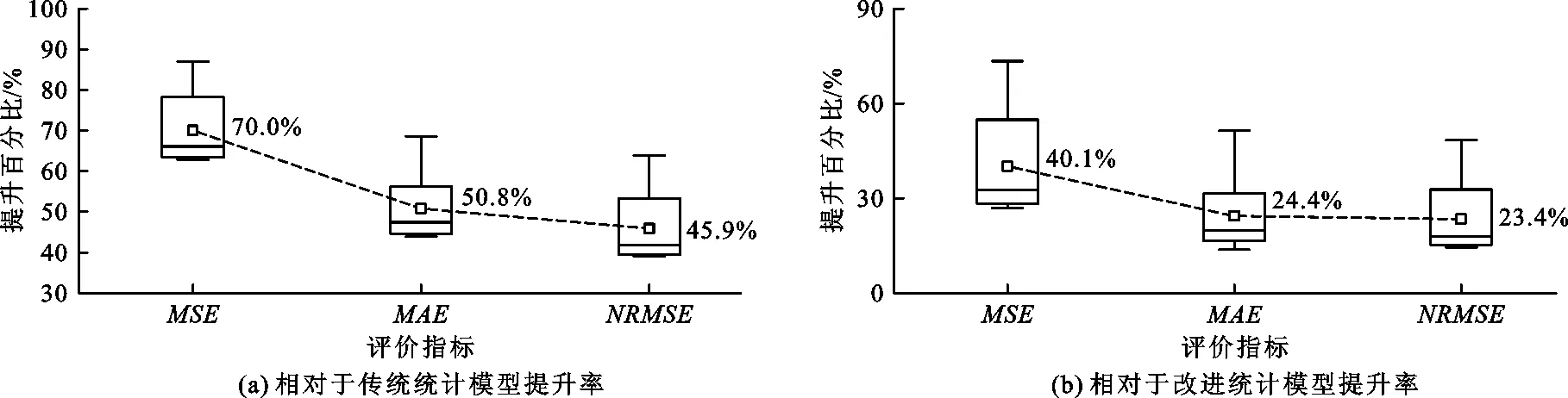
图10 裂缝开合度改进混合预测模型动态预测效果评价

由图10可见，改进混合模型的3个评价指标相对于两类统计模型的改善效果明显。改进混合模型相对于传统统计模型的预测效果平均提升率在45.9%～70.0%之间，其中MSE最大提升率达80%以上；改进混合模型相对于改进统计模型的预测效果平均提升率在23.4%～40.1%之间，其中MSE最大提升率达70%以上，这表明基于改进统计模型的混合模型对单纯的统计模型的改进是合理有效的。