基于引水隧洞安全和经济施工的支护参数优化分析

陈克霖， 梁庆国， 李海宁， 周彩贵

(1.兰州交通大学 土木工程学院， 甘肃 兰州 730070； 2.青海省引大济湟工程建设运行局，青海 西宁 810001； 3.西北水利水电工程有限责任公司， 陕西 西安 710100)

1 研究背景

据不完全统计，自我国建国以来，已建成的地下水电站超过3 000座，已建成的各类引水隧洞长度超过10 000 km，正在建设的引水隧洞超过1 000 km，已规划的引水隧洞工程超过2 000 km[1]。随着“十三五”期间规划的172项重大水利工程的逐步实施，引水隧洞工程无论在数量上还是在规模上均将达到前所未有的高峰。隧洞建设在有效拉动投资、促进就业和改善民生、带动相关产业发展方面具有积极作用[2]。但在给社会带来巨大经济效益的同时，隧洞施工也面临着诸多问题。有关学者从区域、位置、等级和类型等方面对隧道施工事故进行了统计[3-6]，统计结果显示，2006-2016年我国发生隧道施工重大事故共89起，死亡人数452人，其中塌方事故占隧道事故的70%，占比巨大，隧道塌方带来的后果是灾难性的。因此对于隧洞安全施工的研究尤为重要。在隧洞安全性及经济性研究方面，谭智天[7]采用 FLAC3D模拟隧洞施工，分析各阶段隧洞围岩的变形、应力和塑性区分布情况以及衬砌结构的应力分布状况，评价其支护效果并提出了合理的建议措施；张兵等[8]发现由于传统钢拱架对隧洞拱脚处约束不足导致整体支护结构的不稳定；张玉贤等[9]基于二次开发技术与数据库技术，编制了一套水工隧洞施工仿真系统，实现了与工程施工进度相结合的结构安全判断；王鸿等[10]采用理论分析结合数值模拟的方法，运用有限元软件完成了流冰与隧洞撞击的建模与计算分析，得到流冰速度及不同碰撞角度组合工况下对隧洞衬砌作用影响的规律，可为西北寒旱地区冰期输水安全提供支持；郝广伟等[11]在爆破开挖进尺对隧道围岩的影响方面进行了研究，发现开挖进尺越小，其对围岩的影响越小，造成超挖的范围逐渐减小；Napoli等[12]针对复杂地质条件下的工程施工问题，采用RS2程序对不同体积块体随机生成的隧道模型进行分析，可有效解决技术和经济问题；郭敏[13]对比传统小断面长隧洞施工工艺，优化了隧洞施工中的机械化施工技术，解决了小断面隧洞中机械空间利用的问题；Yang等[14]针对大装量楔形切割爆破效果和经济问题，运用相似理论建立不同切割角度的模型试验拟合多项式公式进行研究，提出当切割角为67°时爆破效果最佳，可以最大程度地提高爆破效果和经济效益。

但以往相关研究关于优化参数设计方面较少，尤其是结合安全和经济两方面，鉴于此，依托水利部“172项重大水利工程”之一——“引大济湟工程”，采用正交试验设计及灰色关联度分析法，探讨安全参数和经济指标之间的关系并确定优化参数时的重点对象，优化出既安全又经济的施工方案，为引水隧洞施工提供参考。

引大济湟北干渠工程位于青海省东部，将水资源较丰富的大通河水引入水资源相对贫乏的湟水流域，以减少湟水流域日益加剧的水资源供需矛盾，实现青海省水资源的合理配置和高效利用。项目背景以标段15+610.64 m～23+724.41 m为主，引水线路总长度为8.11 km，共设隧洞6座，总长度为7.52 km，其中7#隧洞长度为1 410 m，8#隧洞长度为1 006 m，9#隧洞长度为1 988 m，10#隧洞长度为1 521 m，11#隧洞长度为1 297 m，此外还有倒虹吸4座、渡槽2座、明渠9 497 m，9#隧洞为最长隧道，6座隧洞长度约占整个引水线路总长的93%。

2 研究方法

2.1 分析方法

正交试验设计(orthogonal design)简称正交设计(orthoplan)[15-18]，是利用正交表科学安排与分析多因素试验的方法，是最常用的试验设计方法之一。采用正交设计建立由初衬厚度、钢拱架间距和开挖进尺3个因素组成的3因素3水平共9个试验工况，结合安全性和经济性，分析其线性相关性和经济造价对隧洞洞室变形及衬砌受力的影响相关性，给出参数优化的重点对象，最后采用灰色关联度理论，通过计算各试验工况关联度优化出综合安全和经济两方面的施工方案。

2.2 数值模型及试验工况设计

本次计算以引大济湟一分干某典型隧洞断面为例，其断面形式为城门洞型。该隧洞施工采用全断面开挖方式，初衬采用C15喷射混凝土，垫层采用C15回填混凝土，二衬采用C20现浇混凝土，钢拱架采用H160×88，锁脚锚杆采用Φ18实心锚杆，引水隧洞断面及支护尺寸如图1所示。地层土体分为两部分，上部为风积黄土，下部为砂岩，隧洞位于砂岩地层，隧洞埋深为70 m，数值模型模拟范围及网格划分如图2所示。根据该引水隧洞的地质勘查报告，模型建立中所选取的材料参数如表1所示。

图1 引水隧洞断面及支护尺寸(标注单位：cm)

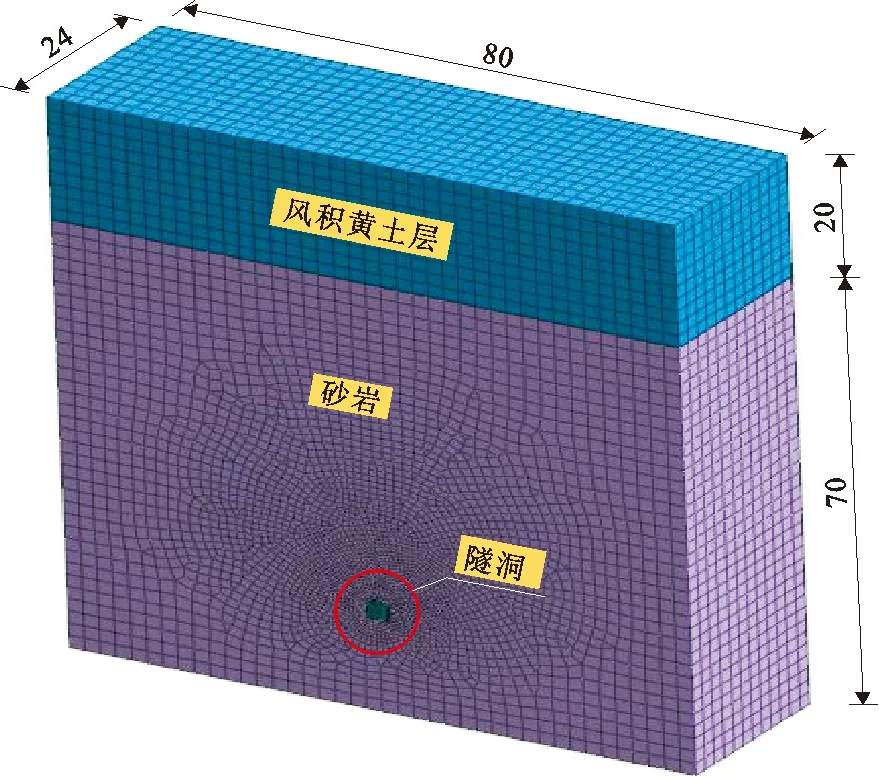
图2 数值模型模拟范围及网格划分示意图(单位：m)

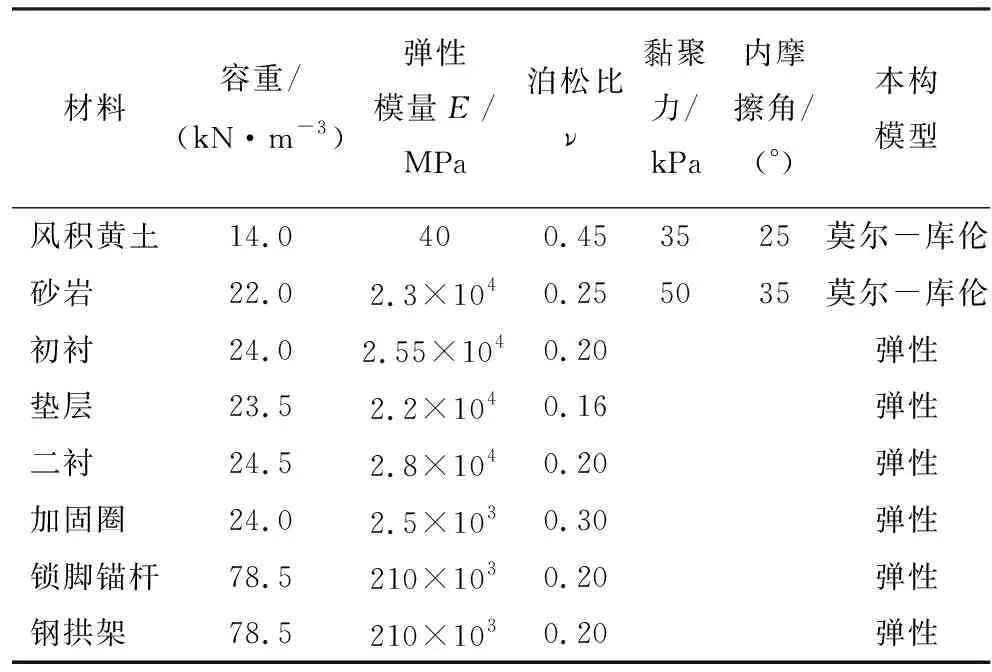
表1 数值模型中材料的物理力学参数取值

所依托的项目隧洞围岩以IV、V级围岩居多，占隧洞工程总量62%，故以Ⅴ级围岩为例进行讨论分析。该隧洞原设计方案为：喷混层厚度为14 cm、钢拱架间距为0.8 m、开挖进尺为1.5 m。在此基础上，每个因素增加两个水平，可认为初衬厚度(因素A)的增大为有利因素，钢拱架间距(因素B)和开挖进尺(因素C)的增大为不利因素，因此各水平排序时不用再考虑随机安排，均按照各水平大小顺序设计，由此确定本次正交试验为3因素3水平，如表2所示。不考虑各因素间的交互作用，本研究以洞室拱顶下沉、底板隆起、边墙水平收敛以及初衬拱顶应力、底板中心应力、边墙中心应力和拱脚应力为考核指标，所研究的引水隧洞全断面开挖9种工况设计如表3所示。

表2 正交试验因素水平表

表3 引水隧洞全断面施工参数正交试验工况设计

完成试验设计后，对9个工况进行MIDAS建模分析，建模过程中严格按照试验表中各数值把控参数，超前支护和二衬均采用实体单元模拟，初衬采用板单元，锚杆和钢拱架分别用植入式桁架和梁单元模拟。

3 引水隧洞安全和经济施工相关分析

3.1 引水隧洞安全性影响因素分析

对正交试验设计的9个工况进行数值模拟后，采用极差法分析影响引水隧洞洞室位移和初衬应力的因素主次顺序，以初衬拱顶应力为例，分析结果列于表4、5。

表4 引水隧洞全断面施工初衬各工况拱顶应力分析结果

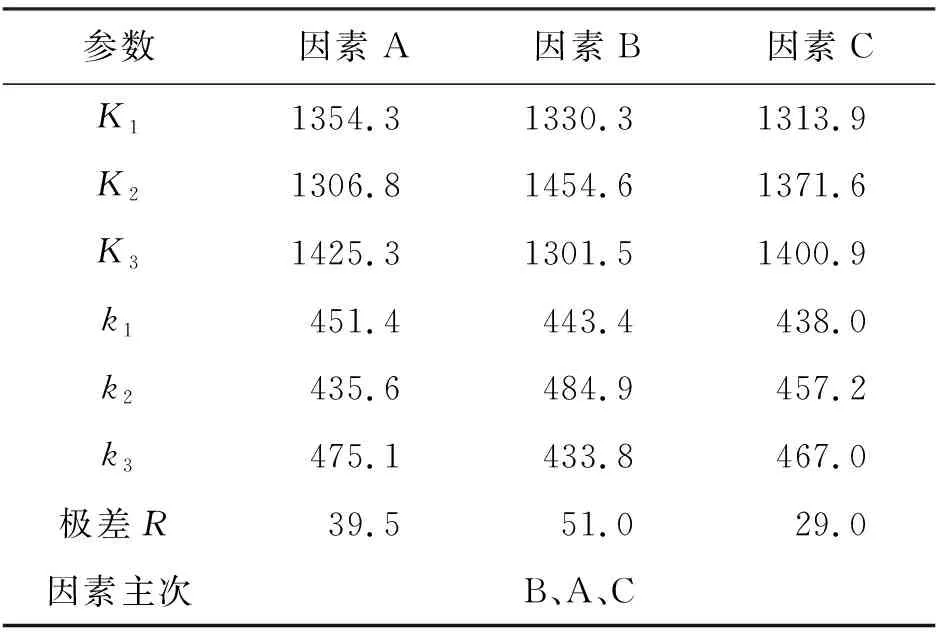
表5 引水隧洞全断面施工不同因素下初衬拱顶应力相关参数 kPa

表5中Ki为同一列中因素水平号i(i=1，2，3)相同的初衬拱顶应力之和；ki为同一列中相同因素水平i下所得初衬拱顶应力的算术平均值，即ki=Ki/s，其中s为同一列中各水平出现的次数，本次试验中s=3(下同)。将影响因素水平作为横坐标，试验指标的平均值为纵坐标，绘制指标平均值随影响因素的变化规律图，各水平按照升序排列，即可明确地看出试验指标随影响因素的变化趋势。其中，初衬拱顶应力平均值随影响因素的变化规律如图3所示。

图3 初衬拱顶应力平均值随影响因素的变化规律

由图3可知，初衬拱顶应力平均值随初衬厚度和钢拱架间距的增大而增大，随开挖进尺的变化趋势不明显，表5中极差法显示，隧洞初衬拱顶应力的影响因素主次顺序为：钢拱架间距、初衬厚度、开挖进尺，即B、A、C。其原因为隧洞开挖后拱顶处的土压力主要由钢拱架和超前小导管承受，钢拱架是主要承受对象。

同理对拱顶下沉、底板隆起、隧洞水平收敛、初衬底板应力、初衬边墙和初衬拱脚应力采用极差法分析其影响因素主次关系，可以得出：隧洞拱顶下沉的影响因素主次顺序为开挖进尺、钢拱架间距、初衬厚度，即C、B、A。其原因为隧洞拱顶处变形的主要受力支护为钢拱架和超前支护，故钢拱架间距越大，则拱顶下沉值越大，同时开挖过程中开挖进尺越大，则其对拱顶的扰动影响越大。隧洞底板隆起、隧洞水平收敛、初衬底板应力、初衬边墙和初衬拱脚应力的影响因素主次顺序均为C、A、B，其原因主要为隧洞底板处无钢拱架，开挖支护后底板隆起的主要受力集中在底板上，主要承受水平压力的支护为初衬，钢拱架承担的压力较小，开挖过程中隧洞洞室受力和变形主要为水平方向，故开挖进尺的大小对上述指标的影响很大，其次才是初衬厚度的影响。

3.2 引水隧洞经济性影响因素分析

引水隧洞开挖支护的过程中也需要充分考虑其经济性，在保障安全的基础上最大程度地节省成本是引水隧洞施工组织的重要内容。通过现场调研，取得实际成本数据，再结合安全施工中的正交试验所列9个工况，对每延米施工所需成本进行计算，分析工程造价和各影响因素的主次情况。现场调研各材料综合单价如表6所示。

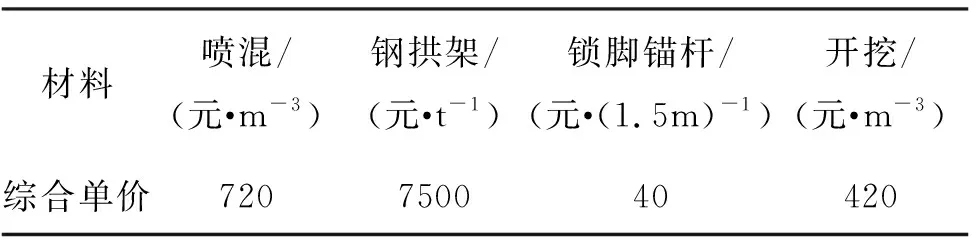
表6 引水隧洞全断面施工现场调研各材料综合单价表

根据表6中各材料的综合单价，按正交试验中9个工况的初衬厚度、钢拱架间距和开挖进尺等3个因素，分别计算各工况下每延米喷混、钢拱架、开挖成本以及总成本，计算结果如表7所示。

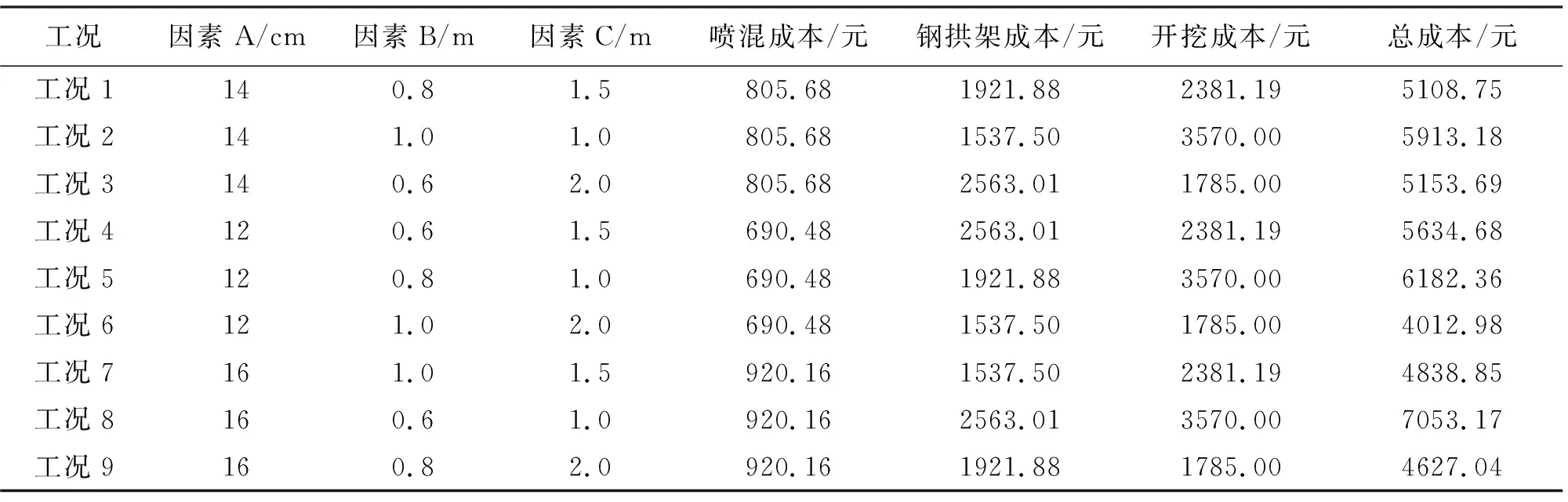
表7 引水隧洞全断面施工各工况每延米成本计算结果

由表7可看出，隧洞开挖施工中各工况下每延米的成本均不相同，各工序材料成本在其总成本中所占的比例也不同，各工况下喷混、钢拱架、开挖成本占总成本的比例如图4所示。

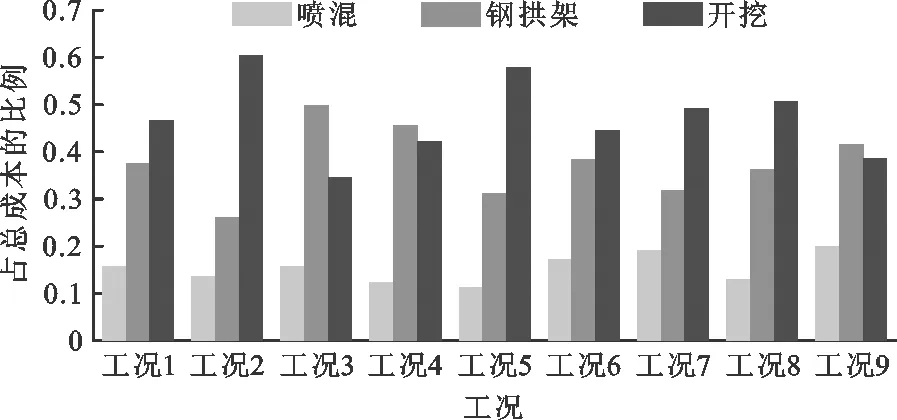
图4 引水隧洞全断面开挖各工况下喷混、钢拱架及开挖成本占比

由图4可见，开挖和钢拱架成本的占比较大，故优选方案时主要以开挖和钢拱架成本所占总成本的比例为考核目标进行分析。以各工况开挖成本占比为例，采取极差分析法研究开挖占比的影响因素主次，如表8、9所示。

表8 引水隧洞全断面施工开挖成本占比优选表

表9 引水隧洞全断面施工不同因素下开挖成本占比相关参数

同理对钢拱架成本占比也采用极差法分析其影响因素的主次关系，最后得出开挖成本占比及钢拱架成本占比的影响因素主次顺序均为：开挖进尺、初衬厚度和钢拱架间距，即C、B、A。

3.3 引水隧洞安全性与经济性综合对比分析

通过分析安全性目标和经济性目标之间的关系，确定支护成本与隧洞洞室位移及初衬应力之间的相关性，分析洞室位移和初衬应力随成本的变化趋势。

隧洞施工中洞室不同位置位移及初衬各部位应力随总成本的变化规律如图5所示。由图5(a)可看出，隧洞洞室不同位置的位移均随总成本的增大而减小，但是变化速率有所不同，其中水平收敛减小速率最大，底板隆起次之，拱顶沉降最小，表明成本的增加对水平收敛和底板隆起的影响较大，对拱顶沉降影响较小。由图5(b)可看出，隧洞初衬各位置的应力均随总成本的增大而减小，且各应力的减小速率相差不大，故而总成本的增加对各位置应力的减小影响相当。其原因为总成本的增加决定了支护措施的加强，导致隧洞位移和初衬应力的减小。

图5 引水隧洞洞室不同位置位移及初衬各部位应力随总成本的变化规律

采用指标隶属度分别求出引水隧洞洞室位移和初衬应力的综合得分，分析两者随总成本的变化规律。指标隶属度计算方法见公式(1)，其最大值为1，最小值为0。给予各指标一定的权重，求得指标隶属度加权值之和作为综合得分。其中隧洞洞室位移主要以水平收敛为主，故拱顶沉降、底板隆起和水平收敛的权重分别取0.25、0.25和0.50；应力综合得分反映了隧洞应力的整体变化，由于混凝土抗压强度远高于抗拉强度，且拱顶和底板处均为拉应力，边墙处均为压应力，拱脚处存在压应力和拉应力，故拱顶、底板、边墙和拱脚应力的权重分别取0.35、0.35、0.10和0.20。

(1)

引水隧洞洞室位移和初衬应力综合得分随总成本的变化规律如图6所示。由图6可知，隧洞位移综合得分和初衬应力综合得分均随着总成本的增大而减小，二者的变化速率也有所不同，洞室位移综合得分的减小速率略大于初衬应力综合得分的减小速率，因而总成本的增加对洞室位移的影响要大于对初衬应力的影响。

引水隧洞洞室不同位置的位移和初衬各部位的应力随钢拱架成本占比的变化规律如图7所示。由图7(a)可知，隧洞洞室位移随钢拱架占比的增大而增大，三者的变化速率有所不同，其中水平收敛的增大速率最大，底板隆起次之，拱顶下沉最小，说明钢拱架成本占比对水平收敛的影响较大，对拱顶下沉的影响较小。由图7(b)可知，隧洞初衬的边墙应力、底板应力和拱脚应力随钢拱架成本占比的增大而增大，且三者的变化速率相差不大，而拱顶应力随钢拱架成本占比的增大而减小。其原因为钢拱架主要承受的压力为拱顶压力，而底板处无钢拱架，对边墙和底板位移的影响较大，钢拱架成本占比的增大意味着开挖进尺和初衬厚度占比减小，从而导致边墙和底板位移的增大速率较大，拱顶位移变化速率较小，钢拱架成本占比增大，则拱顶应力相应减小。

图6 引水隧洞洞室位移和初衬应力综合得分随总成本的变化规律

图7 引水隧洞洞室不同位置位移及初衬各部位应力随钢拱架成本占比的变化规律

采用指标隶属度所得出的引水隧洞洞室位移和初衬应力的综合得分随钢拱架成本占比的变化规律如图8所示。

图8 引水隧洞洞室位移和初衬应力综合得分随钢拱架成本占比的变化规律

由图8可知，隧洞洞室位移和初衬应力综合得分随钢拱架占比的增大而增大，其中洞室位移综合得分的变化速率略大于初衬应力综合得分，表明钢拱架成本占比的增大对洞室位移的影响略大于对初衬应力的影响。

引水隧洞洞室不同位置的位移和初衬各部位的应力随开挖成本占比的变化规律如图9所示。

由图9(a)可知，隧洞洞室位移随开挖成本占比的增大而减小，其中水平收敛的减小速率明显大于拱顶下沉和底板隆起的减小速率，说明开挖成本占比对水平收敛的影响大于对拱顶下沉和底板隆起的影响。

图9 引水隧洞洞室不同位置位移及初衬各部位应力随开挖成本占比的变化规律

由图9(b)可知，隧洞初衬边墙、底板和拱脚应力均随开挖成本占比的增大而减小，其中拱脚应力的减小速率最大，边墙和底板应力减小速率较小，而拱顶应力随开挖成本占比的增大而增大，但增大速率较小，表明开挖成本占比对拱顶应力的影响较小，对其他部位的应力尤其是拱脚应力的影响较大。其原因为随着开挖成本占比的增大，钢拱架和初衬厚度成本占比减小，同时在总成本中开挖成本占比大于钢拱架成本占比，对于钢拱架影响较小的边墙、底板和拱脚处应力来说，决定其大小的主要因素还是开挖进尺。

采用指标隶属度所得出的引水隧洞洞室位移和初衬应力的综合得分随开挖成本占比的变化规律如图10所示。由图10可知，隧洞洞室位移和初衬应力综合得分均随开挖成本占比的增大而减小，其中洞室位移综合得分的减小速率略大于初衬应力综合得分的减小速率，说明开挖成本占比的增大对洞室位移的影响要大于对初衬应力的影响。

4 引水隧洞支护方案优化

灰色关联度评价方法是邓聚龙[19]在部分数据不确定的基础上提出的一种不确定性关联，可以对这些不确定数据进行一定的处理，发现其中某些模糊关联，给出某些影响因素的权重，从而做出相应优化分析。该方法已应用于隧洞围岩稳定性分析、隧洞底害安全性评价及施工方案优化等方面[20-22]。

图10 引水隧洞洞室位移和初衬应力综合得分随开挖成本占比的变化规律

利用灰色关联度评价方法对正交试验设计中的9种工况进行评价计算，评价指标选取与安全性相关的拱顶下沉、底板隆起、边墙收敛、初衬拱顶应力、底板应力、边墙应力、拱脚应力和与经济性相关的钢拱架占比和开挖进尺，以此构建指标矩阵X如下：

对构造矩阵X进行归一化处理，处理后的矩阵R如下：

计算关联系数矩阵ζ：

结合组合权重赋值计算各工况的关联度，计算结果见表10。

表10 各工况关联度汇总

由表10可知，各工况中关联度最大的是工况7，其关联度为0.763，最小的是工况2，其关联度为0.504，关联度越大说明隧洞洞室的稳定性越好且经济方案越优化，工况7为最优方案，即初衬厚度16 cm，钢拱架间距1.0 m，开挖进尺1.5 m。

5 结 论

(1)引水隧洞洞室初衬拱顶应力的影响因素主次顺序为钢拱架间距、初衬厚度、开挖进尺，即因素B、A、C；洞室拱顶下沉、开挖成本占比及钢拱架成本占比的影响因素主次顺序均为因素C、B、A；洞室底板隆起、水平收敛以及初衬底板应力、边墙应力和拱脚应力的影响因素主次顺序均为因素C、A、B。

(2)总成本与洞室不同位置位移、初衬各部位应力及综合得分均呈负相关，总成本对洞室水平收敛和底板隆起的影响最大，对洞室初衬各部位应力的影响相当，对洞室位移的影响总体大于对初衬应力的影响；钢拱架成本占比与洞室不同位置位移、初衬各部位应力(除拱顶应力之外)及综合得分均呈正相关，钢拱架成本占比对洞室水平收敛及拱脚应力的影响最大，对洞室位移的影响总体略大于对初衬应力的影响；开挖成本占比与洞室不同位置位移、初衬各部位应力(除拱顶应力之外)及综合得分均呈负相关，开挖成本占比对洞室水平收敛及拱脚应力的影响最大，对洞室位移的影响总体大于对初衬应力的影响。

(3)计算正交试验9个工况的关联度，关联度最大的为工况7，其关联度为0.763，关联度最小的为工况2，其关联度为0.504。优化后的方案为初衬厚度16 cm、钢拱架间距1.0 m、开挖进尺1.5 m。