液力变矩器分体型叶片设计方法

宁朋刚，蔡森华，田体先

（1.北京航天汇信科技有限公司，北京 100007；2.武汉科技大学，湖北武汉 430081）

0 引言

涡轮机械叶片在运行中，经常在吸力侧受到流动分离的影响，从而降低了效率并降低了叶片的性能。流动分离表现出边界层变厚、出现回流区等现象，从而导致阻力增大、升力减小、压力损失等问题[1]。在液力变矩器中，流动分离控制是一个亟待解决的问题，为此针对这一问题提出了一种分体型叶片设计方法。

1 叶片线型参数化设计

常规叶片线条采用一组坐标数据来表示，无法进行修改。本文采用了解析函数表示翼型或叶片，改变函数参数即可生成一簇新的叶型。由于函数本身的几何意义十分明确，通过调整不同的参数，可按预期的方向生成叶型，实现反向设计。

儒氏翼型解析式分析。

如图1 所示，以大圆圆心为坐标原点，画两个切于B 点的圆，通过小圆圆心和两个圆的切点B 的连线为OB，然后通过复变数解析函数：

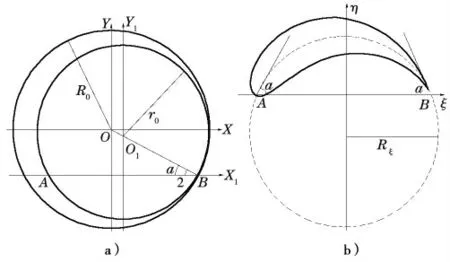
图1 儒科夫斯基翼型

进行大圆周线的保角变换，得出：

式中，x1=x-（R0-r0）cos（α/2），y1=y+R0sin（α/2），将半径为R0的圆周上各点坐标x、y 代入公式进行计算，得到儒氏翼型各点坐标，半径为r0的小圆周上的则为弧线AB，其半径为Rξ：

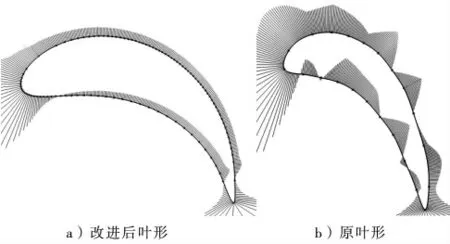
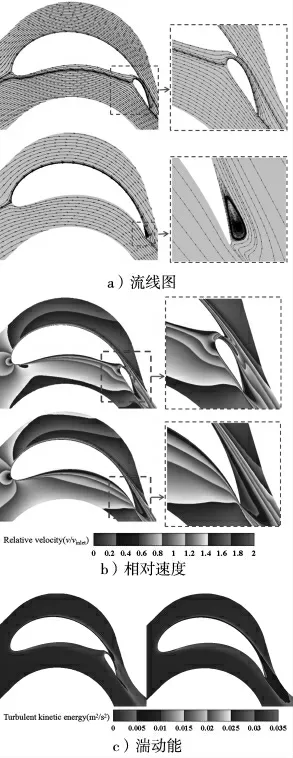
这样就得到了一个完整的翼型，但由于该翼型的尾缘较为尖锐，不符合流体动力学要求，故需要对其进行改进。将大圆沿OO1方向移动L，移动范围0

图2 为改进后叶形与原叶形曲率变化图，通过比较可以看出新叶型曲率变化连续和平滑，尾部有些许波动，原始叶形曲率被分为多段，在不同曲线连接点处曲率变化剧烈，存在着较大波动，说明通过儒氏翼型解析式对原始叶形进行优化之后能够拥有良好的头部形状和平滑的曲率变化，有着更好的流体动力学特性。

图2 新老叶形的曲率对比

2 分体型导轮叶片设计

采用Joukowsky 生成的导轮可以在原有变矩器的基础上降低空化的概率且提高性能，但是并不能完全消除这一现象，而且还可以在此基础上进行改进。本文分析液力变矩器内部流动分离特性及机理，更改叶片结构进一步来抑制流动分离，采用抑制流动分离的一种方法——分体型叶片。

根据前文分析的流场对叶片的分体位置及大小进行分析，在不改变出入口角度和厚度的前提下，对叶型进行分割处理。且分体的两个叶片均采用参数化造型的方法进行造型以便进一步精准优化。

2.1 分体型叶片设计

叶片线型依旧采用Joukowsky 解析函数生成，确定了分体位置之后，尾部用Joukowsky 解析函数在尾缘处生成一个小叶片。该尾部叶片生成满足以下条件：

（1）在不改变导轮入口角度和出口角度的前提下对定子叶片进行分割。

（2）尾翼的切口位置保证在流动分离之前，能够最大限度地抑制流动分离。

（3）为了排除曲率的影响，对后尾翼同样采用Joukowsky 进行设计，且确保出口角度和Rξ保持不变。生成的叶片如图3 所示。

图3 分体型叶型示意

2.2 流场分析

从速度云图和速度矢量图中可以看出，无论叶片是否被切割，由于叶片的大转角特性，其叶片尾缘始终存在着低动能区域，低动能区域的大小决定此流动分离和能量损失的程度。相比于原始叶片，有开槽的叶片的低速区域较小，这说明叶片分体对流动分离具有很好的抑制作用。结合轨迹图可以看出，虽然速度云图中两者均存在着低动能区域，但是原始叶片的尾缘存在着二次流动，二次流动的产生增大了流动损失，有缝翼的叶栅虽然存在着低动能区域，但是还没有形成二次流。这是由于缝翼的存在，压力面的高压流体通过缝隙进入吸力面而提高了吸力面的动能，使将分离的流体重新附着，减小了逆压梯度，抑制了流动分离。流动能是湍流速度涨落方差与流体质量乘积的1/2，根据湍流强度来判断导轮流道中的流动状况，湍流强度越大，流动越不稳定，相应的流动损失就越大。从图4 可以看出，相比于无缝翼，有缝翼的叶栅湍动能值和区域更小，流动更加稳定，流动损失越小，大大提高了叶栅的效率。

图4 流场分布

3 结论

（1）推导出机械臂的逆动力学模型，建立了机械臂末端位姿的实时解算形式。

（2）提出了机械臂基于位置的阻抗控制策略，给出了结合离线轨迹规划的的柔顺控制方法。

（3）对本文提出的控制方法进行了实验平台搭建，结果表明，采用该方法后，机械臂清洗效果可显著提高。