借助数形结合 促进深度学习
2021-02-08马徐仪
马徐仪
【摘 要】随着深度学习理念的施行,越来越多的教师意识到将学生引向数学本质学习的重要性。教师在教学“2、5的倍数的特征”一课时,不应只简单地推理尾数特征,更要引导学生探索其背后的本质原因。借助数形结合,让学生充分经历分类中追溯源头、变化中寻求不变、迁移中促进内化、比较中升华本质的过程,帮助学生在研究变与不变中,理解其本质,推理其特征,进入深度学习状态。
【关键词】数形结合;特征本质;深度学习
查阅近几年“2、5的倍数的特征”一课的研究成果,可以发现越来越多的教師努力把这节看似简单的课上得不那么简单,不再只简单地推理尾数特征,而是引导学生去探索其背后的本质原因。
本课教学一般从探究2或5的倍数特征开始,学生需经历列举、猜想、验证、结论、说理的过程。但在聚焦“为什么只看个位”这一问题时,教师常常会抓住某个学优生的回答,结合小棒或小方块去解释特征本质,其他学生则顺着学优生、教师的PPT演示努力理解尾数特征。这样,对特征本质的理解或者被教师的告知所代替,或者被学优生的思考所代替。要处理好这个问题,教师可以充分利用数形结合,在研究倍数的过程中,提炼本质,自然推导特征,促进深度学习。
【教学过程】
(一)分类中追溯源头
1.数形结合,建立关联
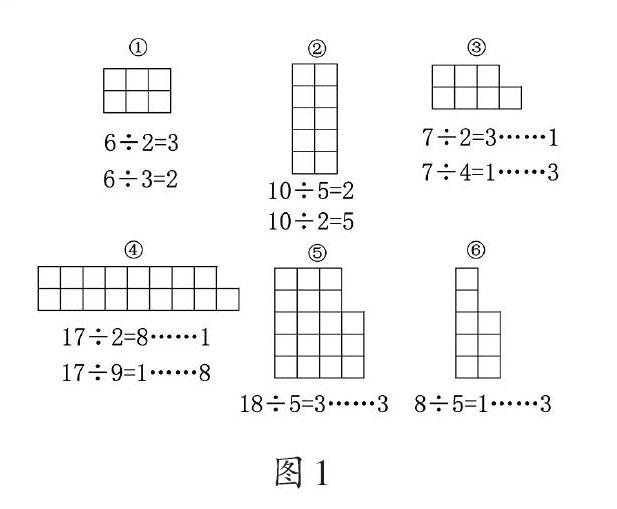
用除法算式表示方格图的意义,学生的反馈情况如图1。
(解析:从横纵两个角度分别观察,①②③④横行、竖列都可以看成每份数,都可以列出2个除法算式,而⑤⑥只能将竖列看成每份数,列出1个除法算式。学生在看方格图列除法算式的过程中,将“数”和“形”建立关联。)
2.分类整理,追溯源头
师:请把它们分分类。
生:拼成长方形的一类(①②),不能拼成长方形的一类(③④⑤⑥)。
生:有余数的一类(③④⑤⑥),另一类没有余数(①②)。
生:把可以列出2种算式的归为一类(①②③④),只能列出1种算式的归为一类(⑤⑥)。
生:把每列数规定为除数,除数是2的一类(①③④),除数是5的一类(②⑤⑥)。
师:我们可以分别以能否拼成长方形、是否有余数、列出算式的个数、除数是否相同作为标准进行分类。
师:6÷2=3,我们就说6是2的——倍数。
师:要使得一个数是另一个数的倍数,需要满足什么条件?
生:把一个数平均分,没有余数。
师:6是怎么分的?
生:把方格2个2个平均分,有这样的3列,或者把方格平均分成2行,每行有3个。
师:用除法表示平均分方格的过程,没有余数时,我们就说被除数是除数的倍数。
(解析:研究一个数倍数的特征本质,教师通常会采用教材提供的百数表,让学生去圈一圈,进而观察、猜想、验证2的倍数的特征,再研究特征本质。笔者没有采用这一做法,而是通过以数解形——用除法算式表示方格图,在分类比较中沟通图、式、倍数之间的关系,追溯倍数源头——平均分。借助方格图,学生回顾除法蕴含的平均分意义;借助除法算式,学生复习倍数概念。除法将倍数与承载平均分意义的方格图联系在了一起。研究一个数的倍数,利用方格图,采用数形结合的方法进行研究能够直指知识本源。)
(二)变化中寻求不变
1.以形助数,积累经验
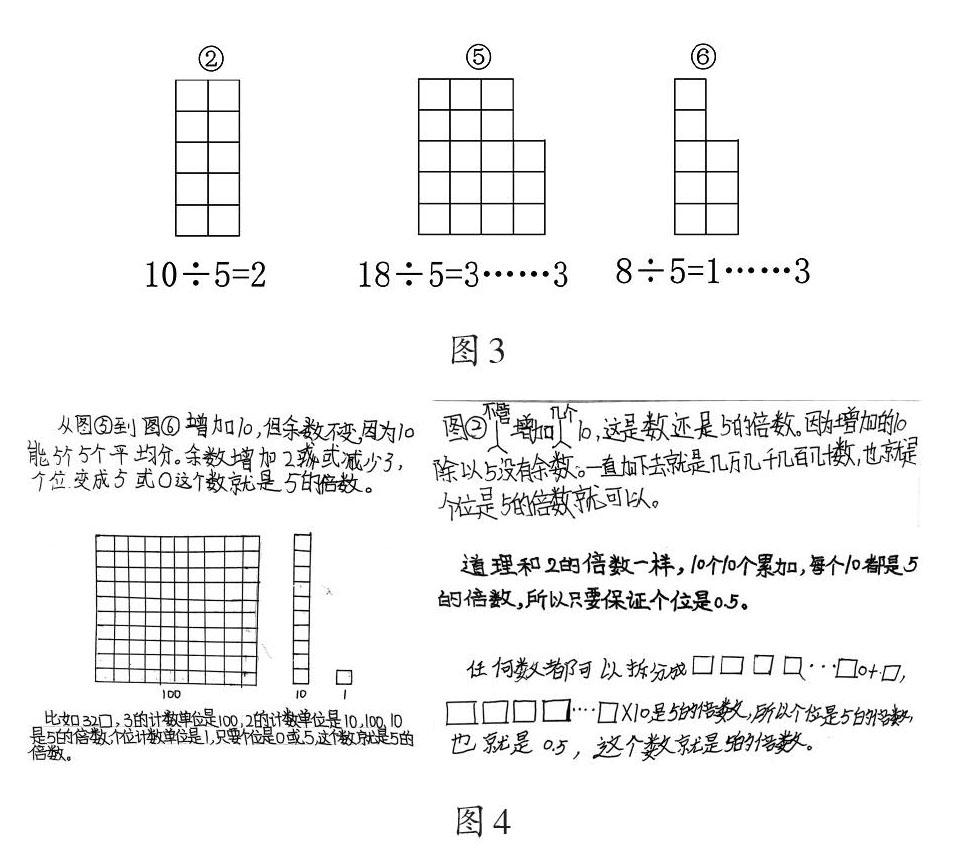
师:结合图说一说,为什么10是2、5的倍数?7为什么不是2的倍数?
生:图②中,10能2个2个分,分成5行;5个5个分,分成2列。图③中,2个方格为1列,分了3列后还剩下1个。
师:从图上看,满足什么条件就能找到一个数的倍数?
生:只要能拼成长方形就可以。因为只要能拼成长方形,总数就是每份数或份数的倍数。
(解析:以形助数,让学生结合方格图解释一个数什么时候是另一个数的倍数,什么时候不是另一个数的倍数,再一次加深了学生对成倍数关系所拼成的图形是长方形的印象。这一结论为后续探索倍数特征的本质积累了活动经验。)
2.累加变化,寻求不变
师:图④中的17,是不是2的倍数?
生:2个1列,分成8列,还剩1个,不是2的倍数。
师:有没有更快的想法?
生:7到17增加了10,10个方格2个2个分没有剩余,所以我们根据前面“7不是2的倍数”的结论,可以推测17也不是2的倍数,余数仍然是1。
师:改成27,会怎么样?
生:也不是2的倍数。因为27和17相比,又多了10,我们知道增加一个10不会产生新的余数。
师:余数还是?
生(全体):1。
师:如果接着增加下去,变成37、47、57、67……你觉得变到什么时候,它就是2的倍数?
(学生思考中,没有人举手)
师(追问):变成107总行了吧?
生:从27变到107,增加了8个10,不管有多少个10,都能2个2个平均分,余数不变。
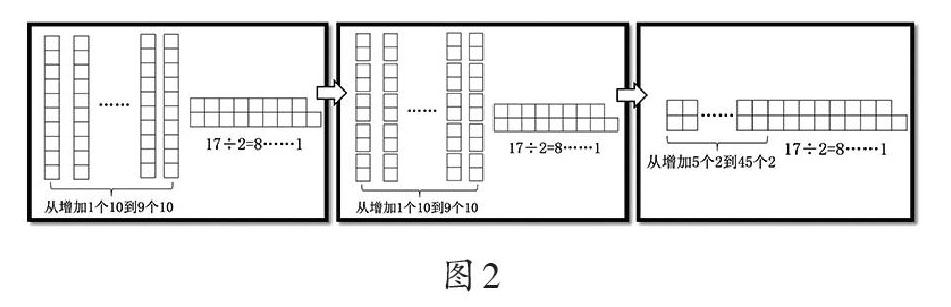
师:同学们一起来看一看,是不是这样的?(PPT演示,如图2)
师:你有什么发现?
生:十位、百位数位上的数字不管怎么变,除以2的余数不变。
(解析:“2的倍数的特征只要看个位”的结论,教学中一般是从学优生口中得到的,教师再以某个数为例,运用数形结合的方式进行再次解释。本环节以形助数,学生2个2个平均分方格,在10个10个累加变化中自然感受、理解十位、百位,甚至想象千位上的数字变化,但余数没有发生变化的原理。)
3.发现特征,解释本质
师:要使得这些数都变成2的倍数,你们打算怎么做?
