基于改进型负载转矩观测器的永磁同步电机滑模控制

颜伟平，王 兵，刘 凯，余 鑫，李江坪

（1.湖南工业大学 电气与信息工程学院，湖南 株洲 412007；2.湖南工业大学 电传动控制与智能装备湖南省重点实验室，湖南 株洲 412007）

1 研究背景

永磁同步电机（permanent magnet synchronous motor，PMSM）具有效率高、扭矩大、转速性能好等优点，被广泛应用在制造、电动汽车、工业生产等领域中[1-2]。PMSM 控制是参数时变的复杂系统，发生负载扰动或内部参数摄动时，会影响PMSM 的稳态误差、动态性能和调速范围等性能参数[3-4]。采用传统的PI 控制无法较好抑制负载转矩扰动对系统的影响，系统的抗负载扰动能力较差，不能达到高性能控制要求[5-6]。而滑模变结构控制（sliding mode control，SMC）具有动态响应快、对负载扰动及参数摄动具有强鲁棒性等优点，满足高性能控制要求，逐渐引起了学者们的重视[7-8]。

近些年，不少国内外学者将滑模变结构控制应用在PMSM 高性能伺服控制系统中[9]。如文献[10]设计了一种开环扰动观测器，并引入积分补偿，具结构简单的优点，且提高了系统的鲁棒性和快速性。文献[11]考虑到负载时变的控制场合，提出了负载转矩滑模观测器，能较好地观测负载转矩，有效削弱抖振，但观测器未利用其反馈增益值优势，在观测性能上稍显不足。文献[12]在传统观测器积分环节中引入比例环节对负载转矩进行观测，提高了观测收敛速度，但由于转速环采用传统PI 控制，抗扰性能较差。文献[13]采用滑模速度控制器代替传统PI 控制器，并改进了控制器中指数趋近率，在滑模面中引入转速误差积分项减小系统静态误差，提高了系统的抗扰能力。

为提高PMSM 控制性能，本文采用一种改进指数趋近率的滑模速度控制器取代传统滑模速度控制器，以提高系统的响应速度；为提高对负载转矩观测响应速度并减少转矩观测的波动性，将观测的负载转矩前馈补偿至电流调节器中，并在传统观测器中加入可变增益算法。设计的改进型负载转矩观测器，能减小负载波动、缩短收敛时间，进一步提升了观测器性能，减少负载扰动对控制系统的影响，提高了系统鲁棒性。

2 PMSM 数学模型

忽略铁心涡流与磁滞损耗，考虑转子上无阻尼绕组等影响，采用id=0 的PMSM 转子磁场定向控制，建立PMSM 在d-q轴旋转坐标系下的数学模型，电压方程如下：

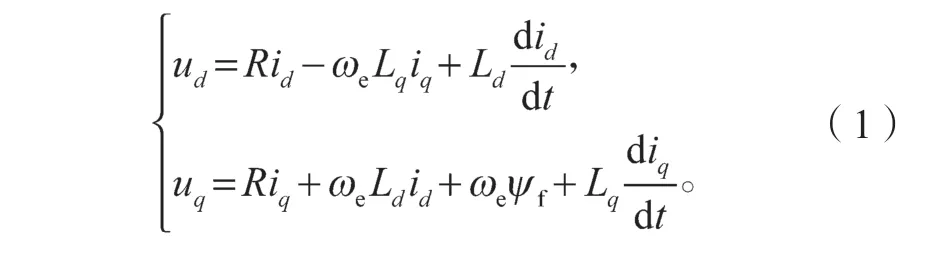
对于凸极式PMSM 矢量控制系统（采用id=0 控制方式），其电磁转矩方程如下：

PMSM 运动方程：

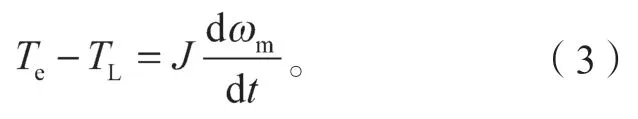
式（1）～（3）中：ud、uq分别为d-q轴的电压；

Ld、Lq分别为d-q轴的电感；

id、iq分别为d-q轴的电流；

Te为电磁转矩；

J为转动惯量；

ψf为永磁体磁链；

R为定子电阻；

ωm为转子机械角速度；

ωe为转子电角速度；

TL为负载转矩；

p为电机极对数。

3 滑模速度控制器

3.1 滑模速度控制器设计

引用文献[11]中滑模速度控制器，定义PMSM系统的状态变量如下：

式中：ω*为电机给定转速；

ω为电机实际转速。

由式（2）～（4）可知：

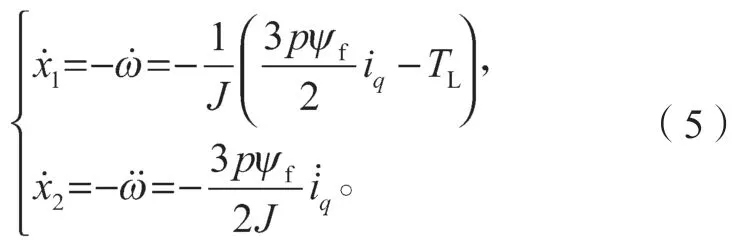
对式（5）进行 化简，令D=1.5pψf/J，u=i·q，可得系统状态空间方程为

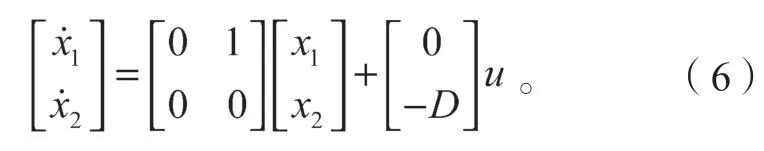
为使系统更好地达到稳态，选择滑模面函数为

式中，c为滑模面参数，且c＞0。

对式（7）求导可得：

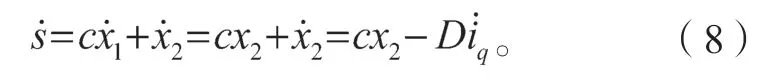
为改善滑模趋近运动中的动态品质，引用文献[11]中的指数趋近律，其表达式为

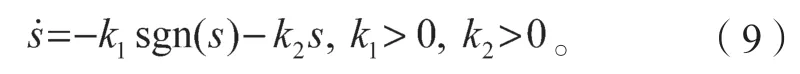
式中：-k1sgn(s)为等速趋近项；

-k2s为指数趋近项。

k1、k2两个系数分别决定滑模面的抖振和趋近过程的运动品质。

为提高系统响应速度，在传统指数趋近率的基础上进行改进，改进的趋近律为

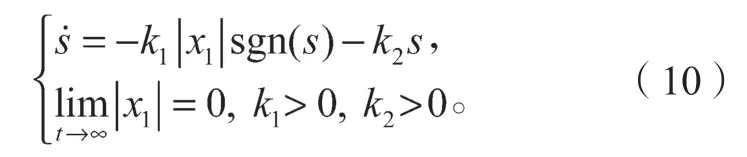
在等速趋近项中加入转速误差绝对值|x1|，使系统转速误差绝对值|x1|与系统状态变量在趋近滑模面过程中的速度k1相联系。当系统状态变量离滑模面较远时，此时|x1|较大，状态变量将以-k1|x1|sgn(s)-k2s的速度趋近滑模面，当状态变量靠近滑模面时，指数项近似为0，系统以-k1|x1|sgn(s)速度将状态变量不断减少，逐渐减少到0。

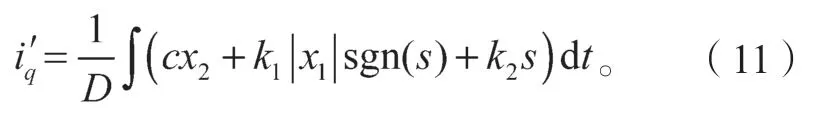
控制器中含有积分项，将控制量进行滤波，可削弱系统抖振、减少系统的稳态误差，提高系统稳定性。

3.2 稳定性分析

定义Lyapunov 函数为

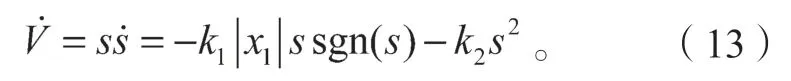
式中，k1＞0，k2＞0，s·sgn(s)≥0，故，此结果表明系统跟踪误差能在有限时间内收敛到零，系统能稳定运行。

4 负载转矩观测器

4.1 传统负载转矩观测器

滑模控制主要通过增大控制器中不连续项的幅值来抑制参数变化和外部负载扰动对系统的影响，但幅值增大会引起滑模固有抖振。为解决滑模控制系统抖振与抗扰性之间的矛盾，利用观测器实时观测负载扰动变化，将观测值前馈补偿至电流调节器中，以降低滑模控制中不连续项幅值，削弱系统抖振问题，实现对负载扰动的快速抑制。

根据PMSM 电磁转矩与运动方程，对于恒定的阶跃性负载，在变化周期内可认为是一恒定值，即，将负载转矩与电机机械角速度作为状态变量，构成PMSM 状态方程：

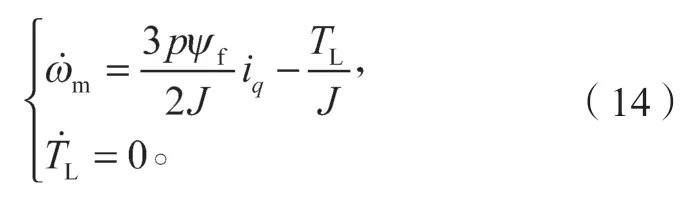
在式（14）基础上，以负载转矩与电机机械角速度为观测对象，建立如下传统负载转矩观测器：

g为观测器的反馈增益；

k为观测器的滑模增益；

根据式（15）搭建传统负载转矩观测器的原理框图，如图1 所示。

图1 传统负载转矩观测器原理框图Fig.1 Block diagram of the traditional load torque detector

将式（14）与式（15）相减，得到传统负载转矩观测器误差方程如下：

式中：e1为机械角速度估算误差，且e1=-ωm；

e2为负载转矩观测误差，且e2=-TLe2；

定义观测器滑模面为s1=e1=-ωm=0。

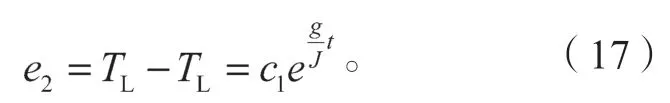
式中：c1为常数。

随着时间t的变化，观测误差e2以指数方式逐渐减少到0，且反馈增益g的取值范围与辨识速度与转矩观测波动性相关。

在传统观测器中，反馈增益g的取值大小对负载转矩观测结果影响较大。反馈增益g越大，观测转矩波动性越小，但观测转矩辨识速度越慢；反馈增益g越小，观测转矩速度越快，但观测转矩波动性越大。出于对此问题的考虑，在传统负载转矩观测器中，综合考虑负载转矩的观测速度与波动性，将反馈增益g取一个折中值，但这会舍弃大反馈增益时的波动性小和小反馈增益时的观测速度快的优势。

4.2 改进型负载转矩观测器

为了充分利用反馈增益g在高、低值时的优势，本文在传统负载转矩观测器基础上，根据两相邻时刻负载转矩观测值大小，设计一种可变增益算法，在负载转矩观测值变化小时，给予反馈增益g较大值，使观测结果波动性小，稳定性更强；在负载转矩观测值变化大时，给予反馈增益g较小值，使观测速度快，最终得到观测速度快和波动小的结果，实现反馈增益g参数自整定。可变增益原理图如图2 所示。

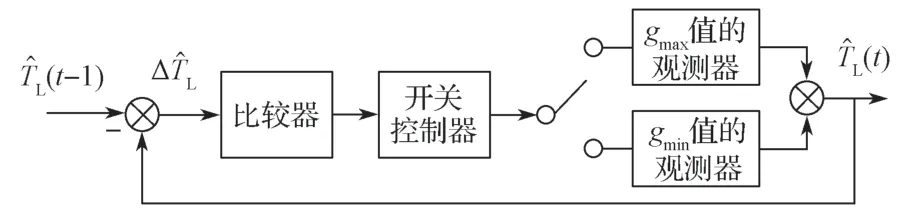
图2 可变增益算法原理图Fig.2 Schematic diagram of the variable gain algorithm

在改进型负载转矩观测器中，可变增益算法采用s 函数进行编写，在算法开始阶段，先选取gmin，确保算法能快速计算辨识结果，设置一个比较值误差ε，将负载转矩观测值前后时刻差值与ε进行比较以判断当前观测的波动情况，当大于ε认为波动大，而小于ε认为波动小。可变增益算法具体流程如图3 所示。

图3 可变增益算法流程图Fig.3 Variable gain algorithm flow chart

将可变增益算法加入到传统负载转矩观测器中，对反馈增益g实现参数自整定，得到改进型负载转矩观测器原理框图如图4 所示。

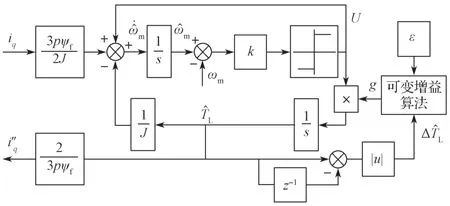
图4 改进型负载转矩观测器原理框图Fig.4 Block diagram of the improved load torque observer

在改进型负载转矩观测器对负载转矩精确测量的情况下，将负载转矩的观测值转换成转矩电流分量前馈补偿至电流调节器的输入，作为系统负载扰动的补偿输入，对滑模速度控制器的输出电流进行补偿。结合式（11），得到的转矩电流给定为

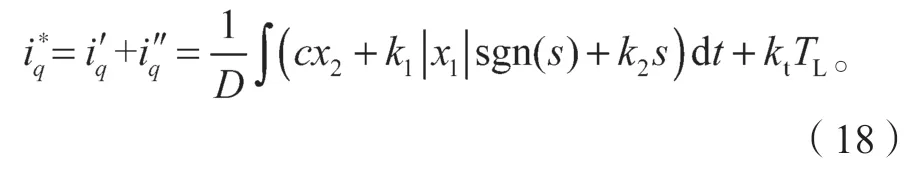
式中，kt为转矩观测补偿系数，由式（2）中电磁转矩与电流之间关系，可以得出kt应取2/(3Pψf)。

比较式（11）与式（18）可得，当负载扰动发生时，为保证电机转速恒定，则需选取较大k1、k2值来提供充足的给定电流值；而式（18）将负载转矩观测值前馈补偿至电流调节器中，在不需要较大k1、k2值的情况下就能提供负载扰动时所需的给定电流，减少滑模速度控制器的不连续幅值及输出负担，能较好地抑制系统的抖振。

5 系统仿真与结果分析

为验证本文设计的改进型负载转矩观测器的正确性及改进SMC 转矩前馈补偿控制方法的可行性，通过Matlab/Simulink 软件进行仿真研究，根据图1搭建的传统负载转矩观测器仿真模块如图5 所示，系统仿真模型如图6 所示，根据图4 搭建的改进型负载转矩观测器仿真模块如图7 所示。

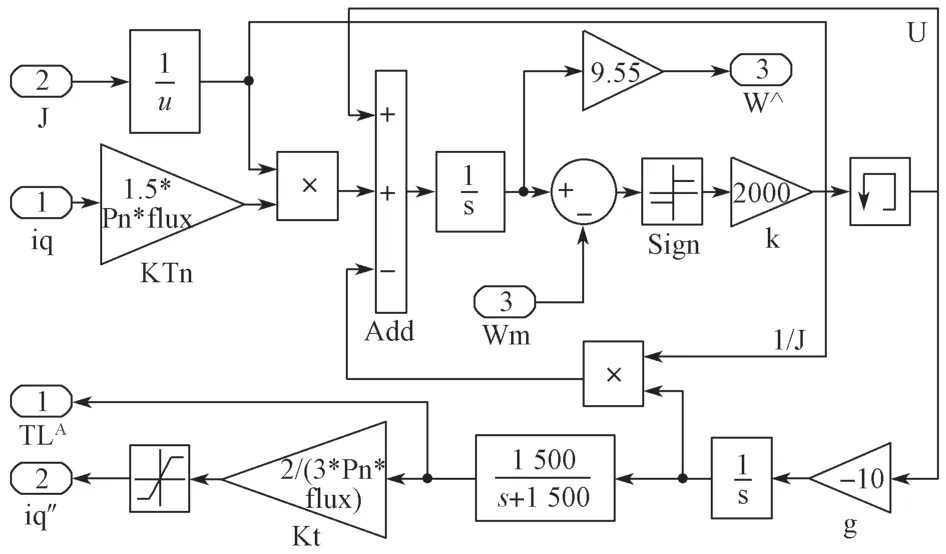
图5 传统负载转矩观测器仿真模块Fig.5 Traditional load torque observer simulation module

图6 系统仿真模型Fig.6 System simulation model

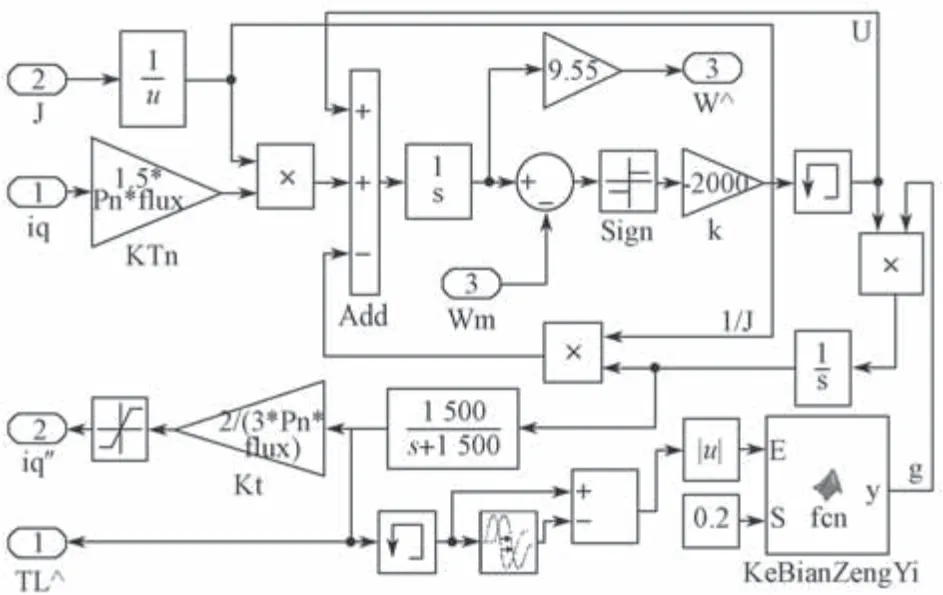
图7 改进型负载转矩观测器仿真模块Fig.7 Improved load torque observer simulation module

选取的PMSM 参数如表1 所示。

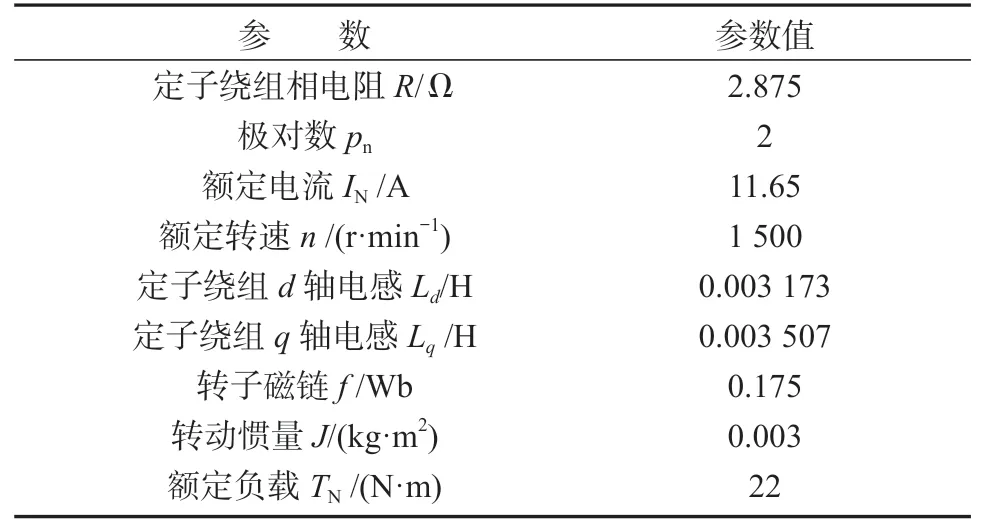
表1 PMSM 参数设置Table 1 PMSM parameters setting

5.1 转速突变分析

给定额定负载转矩为22 N·m，设定系统初始转速为1 500 r/min，0.2 s 时转速突减至1 200 r/min，0.4 s 时转速突增至1 400 r/min。图8 为两种控制策略下转速响应仿真结果。

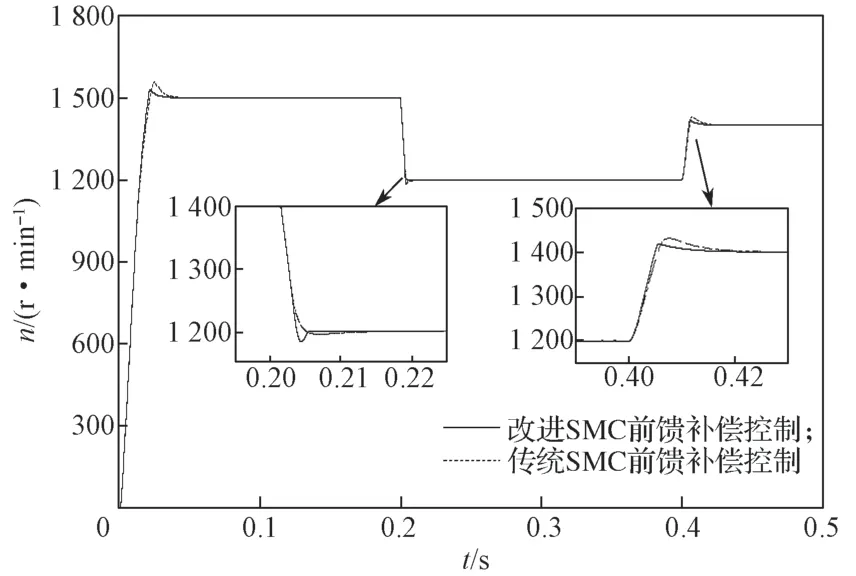
图8 两种控制策略下转速响应波形对比Fig.8 comparison of speed response waveforms under two control strategies

由图8 可以看出，传统SMC 前馈补偿控制的超调较大，调节时间长；而改进SMC 前馈补偿控制的超调较小，响应速度较快，与传统SMC 控制对比优势明显。

5.2 负载突变分析

为验证系统在负载突变时的控制性能，针对电机在不同转速工况下，进行突加、减负载转矩。给定初始负载转矩为0 N·m，在0.2 s 时由0 N·m 突增至额定负载22 N·m，0.4 s 时突减至0 N·m。

给定系统转速1 500 r/min，两种控制策略下系统突加、减负载转速响应仿真结果如图9 所示。

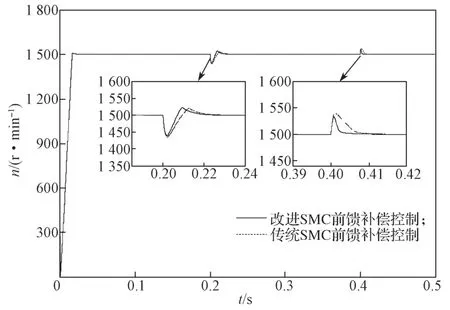
图9 突加、减负载时两种控制策略转速响应波形对比Fig.9 comparison of the speed response waveforms of the two control strategies during sudden load increase and load decrease

由图9 可以看出，空载启动下，两种控制策略超调量均较小，无较大差异，但在突加、减负载时，两种控制策略差异明显。突加额定负载时，传统SMC前馈补偿控制转速有65 r/min 左右的跌落，经过26 ms 回到给定转速；改进SMC 前馈补偿控制转速有60 r/min 左右跌落，只需19 ms 左右回到给定转速。卸负载时，传统SMC 前馈补偿控制转速有34 r/min上升，经过10 ms 回到给定值，而改进SMC 前馈补偿控制转速有30 r/min 上升，只需6 ms 即回到给定转速。相比而言，改进后系统鲁棒性更好，响应速度更快。

给定系统转速为1 500 r/min，在两种控制策略下电机在不同负载转矩作用下，加、减负载时转速变化值和调节时间如表2 所示。

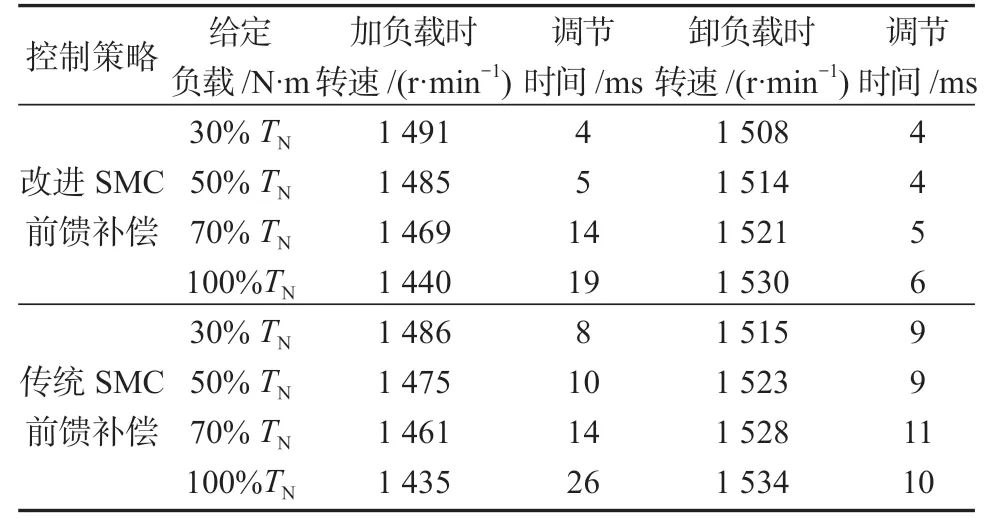
表2 两种控制策略下电机转速变化值和调节时间Table 2 Motor speed change value and adjustment time under two control strategies

分析表2 中数据可知，在不同负载转矩工况下，改进型SMC 前馈补偿控制较传统SMC 前馈补偿控制具有转速波动较小、响应速度较快、调节时间更短，能较好地抑制负载变化对系统转速的影响，抗扰动性能较强。

5.3 反馈增益系数对负载转矩观测的影响分析

负载转矩观测器基于滑模控制实现对负载转矩的观测，并将观测的负载转矩前馈补偿至电流调节器中。观测器中反馈增益g的取值会影响对负载转矩观测的结果，传统SMC 前馈补偿中反馈增益g是取折中值进行仿真分析。本文按控制指标需求先设定两个极值大致范围，然后用递推算法确定最佳值，选取反馈增益系数为gmax=-0.8，gmin=-10，折中值g=-2，对永磁同步电机的额定负载转矩进行观测，仿真结果如图10 所示。

图10 不同g 值下传统负载转矩观测器实际转矩值与观测转矩值Fig.10 The actual torque value and the observed torque value of the traditional load torque observer under different g

图10a、10b、10c 分别为传统负载转矩观测器在取小反馈增益和取折中值以及大反馈增益情况下的转矩观测波形。从收敛速度上看，当反馈增益取gmin=-10 时，收敛时间为0.004 s，收敛速度最快；当取折中值g=-2时，收敛时间为0.008 s，收敛速度较快；当取gmax=-0.8 时，收敛时间为0.025 s，收敛速度最慢。因此，反馈增益系数越小，负载转矩的观测波形收敛速度越快。此外，随着反馈增益系数变小，收敛速度变化趋势逐渐降低，当收敛速度达到一定值后，减少反馈增益系数对负载转矩的收敛速度的提高作用变小。从波动幅值上看，当反馈增益取gmin=-10 时，波动范围在0.006 N·m 左右，波形振荡幅值最大；当取折中值g=-2 时，波动范围在0.004 N·m 左右，波形振荡幅值较低；当取gmax=-0.8 时，波动范围在0.002 N·m 左右，波形振荡幅值最小。通过设定的3 个不同反馈增益值仿真结果可知，反馈增益系数越小，负载转矩观测的振荡幅值越大，波动性越强；反馈增益越大，负载转矩观测的振荡幅值越小，观测精度越高。

5.4 可变增益算法对负载转矩观测器的影响分析

在改进负载转矩观测器中，采用s 函数编写可变增益算法，取gmax=-0.8，gmin=-10 作为增益变换值，通过不断的参数调整，设置比较值ε为0.2[14]，改进型负载转矩观测器观测的仿真波形如图11 所示。

图11 改进型负载转矩观测器实际转矩值与观测转矩值Fig.11 The actual torque value and the observed torque value of the improved load torque observer

从图11 可知，在可变增益算法下，改进负载转矩观测器对负载转矩的观测收敛时间约为0.004 s，观测转矩波动范围在0.002 N·m 左右。

不同反馈增益g下，传统负载转矩观测器与改进型负载转矩观测器对负载转矩观测效果对比，如表3所示。从表3 可以看出，可变增益算法解决了传统负载转矩观测器中小反馈增益导致转矩观测波动大的问题，以及大反馈增益收敛时间长的问题，收敛时间和波动幅度指标都优于折中增益算法的。可变增益算法能快速跟踪负载转矩变化值，将传统负载转矩观测器的固定反馈增益优点保留，对缺点进行改进，达到了较好的观测效果。

表3 不同算法下观测效果对比Table 3 comparison of observation effects under different algorithms

6 结语

本文在对PMSM负载转矩观测器研究的基础上，通过改进滑模速度控制器指数趋近率函数，在传统负载转矩观测器基础上，加入可变增益算法，得到一种改进型负载转矩观测器。改进型负载转矩观测器提高了对负载转矩的辨识速度，减少了观测波动，有效抑制了系统抖振，提高了系统抗干扰性能，对永磁同步电机抗负载扰动研究有一定的参考价值。