基于分离-重构技术的6R机器人逆解新方法
2021-02-07于权伟杨加超谢楚政
于权伟,李 光,肖 帆,杨加超,谢楚政
(湖南工业大学 机械工程学院,湖南 株洲 412007)
1 研究背景
机器人运动学包括正运动学和逆运动学。正运动学是通过在工作空间内选择一组关节角来获得机器人末端执行器的姿态,对应于一个唯一解。逆运动学是给定目标位姿求解对应的关节角,其解有多个。
目前,运动学建模主要采用D-H 坐标法[1]和螺旋法[2]。D-H 坐标法虽然应用更广泛,但也存在一些不足之处,主要体现在用于标定D-H 模型的运动学参数不连续,当机器人相邻关节轴平行或接近平行时,会产生奇异性;而且D-H 坐标法需要为每个连杆建立局部坐标系,导致坐标系不灵活。而螺旋理论是应用李群知识和旋量理论提出的一种依据旋量指数积公式的运动学模型,从而推导出机器人运动方程的完整几何表示,简化机器人机构的分析,并提供串联机器人的机构参数化表示方法;利用螺旋理论建立机器人正向运动学模型,仅需要建立基础坐标系和工具坐标系,便能从整体上描述机器人的运动。
逆运动学是已知末端执行器的位姿,求解相应关节变量的过程[3]。逆运动学求解的实质是完成机器人工作空间到关节空间的映射。逆运动学方程组具有高维、非线性的特点,求解复杂且不易求出。在逆运动学中,多采用解析法、几何法、代数法和矩阵理论相结合[4]来求解6R 机器人的逆运动学问题,从而进一步求得逆运动学解。
文献[5]中采用的封闭解法,在通用性上不如数值法,但其函数构造简便、计算方便快捷。其对满足pieper 准则的机器人具有通用性,利用矩阵求逆的方法生成12 组非线性方程,并利用代数法求解该方程,获得机器人各关节角度变量的8 组解。文献[6]中利用齐次坐标变换矩阵推导出逆运动学问题的解析解,其方法在计算逆向运动学的过程中需要进行多次矩阵变换,导致求逆解速率较低。文献[7]中采用几何、代数方法和子问题进行逆运动学求解,在Matlab中利用代数消元法求解关节4和5中的奇异点;当θ5=90°时,导致θ4无法进行求解。文献[8]中针对后3 个关节轴线相交于一点的6R 工业机器人,采用臂腕分离的方法求其逆解,即将其分为两个3R 部分,虽然该方法可以避免矩阵求逆的运算,但在求逆解中:若末端位置的x、y都为0,则θ1的变化不影响腕点的位置;若连杆坐标系原点连线O2O3与O3O4共线,则θ2的两个解相等;若θ5为零,则关节4 和6 的转轴共线,导致θ4和θ6无法进行求解。文献[9]中将PUMA-560 机器人逆运动学求解分为位置求解和姿态求解两个过程,首先使用D-H 坐标法进行位置求解得到关节角θ1、θ2和θ3,然后使用单位四元数的方法求解出θ4~θ6,但求逆解过程中表达式繁琐,导致运算速率较低。文献[10]中将机器人末端执行器位姿0Th逆解问题转化为末端腕部点位姿0T6的逆解问题,排除0Th中含常量d6的多项式,简化求运动学逆解复杂度。通过反变换法求6R 机器人逆解,但求解关节4 中存在奇异点;当s5=0 时,导致θ4无法进行求解。
针对上述问题,在文献[5-10]的基础下,本文提出一种利用分离-重构技术求后3 个连续关节轴线相交于一点的6R 机器人逆解新方法。首先,采用螺旋理论的POE(exponential of product)法对PUMA-560 机器人进行正向运动学建模,为后续求逆向运动学解提供必要准备;然后通过公式变形,推导出机器人可分离的结论,并详细介绍分离点的选取与重连的几何约束条件;其次,证明了以子机器人重新结合为一个完整机器人的几何约束条件,推导出关节角的求解公式,并对每个关节角进行求解;最后,以仿真实验结果证明了本文所提方法的有效性。
2 机器人结构分离
在研究机器人运动学中,主要采用D-H 坐标法建立正向运动学模型,然后通过矩阵逆乘推导出求逆解的方程。事实上,这其中已体现将机器人结构分离的思想,但由于D-H 坐标法不具备直观的几何意义,从而导致该思想没被提炼出来。虽然文献[11]已经提出将6R 机器人分离为两个3R 子机器人的方法,但并未从理论上对其进行推广。腕部关节结构简图如图1 所示。
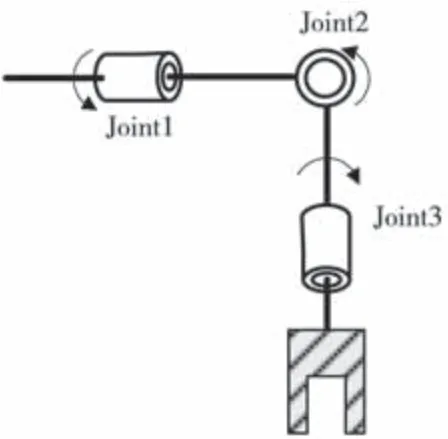
图1 腕部关节结构简图Fig.1 Schematic diagram of wrist joints
从图1 可以看出,6R 机器人腕部关节结构中,后3 个关节为轴线交于一点。本文使用几何意义更明确的螺旋理论,首先证明n自由度机器人的可分离性,再详细证明如何分离最后3 个关节为轴线交于一点的6R 机器人。
2.1 旋量和刚体运动
根据旋量理论,刚体空间运动可描述为由绕某一轴的旋转和平移复合而成。设表示刚体旋转轴的方向,r为轴上的一点,则刚体运动旋量可用ξ=[ω,ν]T表示,其中ν=q×ω,ξ同样可以被称为刚体的螺旋轴,则w的反对称矩阵为

以反对称矩阵为推广,可将运动旋量ξ的矩阵形式记为

刚体运动指数坐标如下:设ω(ω∈R3)表示旋转轴方向的单位矢量,θ(θ∈R)为转角。对于刚体每一个旋转运动,都有一个旋转矩阵R(R∈SO(3))与之对应,具体关系由Rodrigues 公式[12]给出:

式中||ω||=1。
所以一般刚体运动指数坐标可表示为

2.2 串联机器人正向运动学的指数积公式
各关节运动由相关联关节轴线的运动旋量产生,如果用ξ表示该关节轴线的单位运动旋量坐标,则沿此轴线的刚体运动可表示为
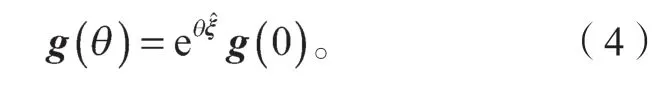
定义机器人的初始位形为机器人当θ=0 时的位形,并用表示机器人位于初始位形时的惯性坐标系与工具坐标系间的刚体变换。对于每个关节都可构造一个单位运动旋量,这时除第i个关节的其他关节均固定于初始位形(θj=0),结合公式,可得到机器人正向运动学的指数积公式,为
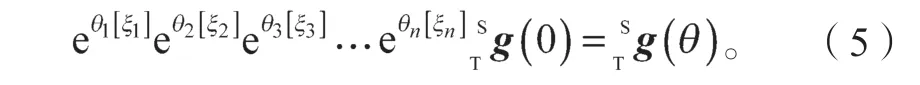
2.3 n 自由度机器人可分离证明
式(5)可变形为
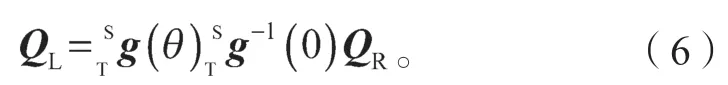
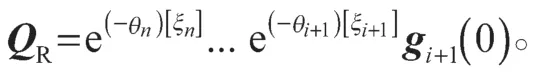
QL表示前i个关节的正向运动学,QR表示后n-i个关节的正向运动学。式中gi(0)是一个可逆的位姿矩阵,其原点位于第i+1 个关节轴轴线的原点,姿态与惯性坐标系一致,其中,第i+1 个关节轴线的原点,定义为关节i与关节i+1 两轴轴线的公垂线与关节i+1 轴线的交点。下文中所说原点均以此定义。图2 为子机器人R 基座标系未变换的情况。
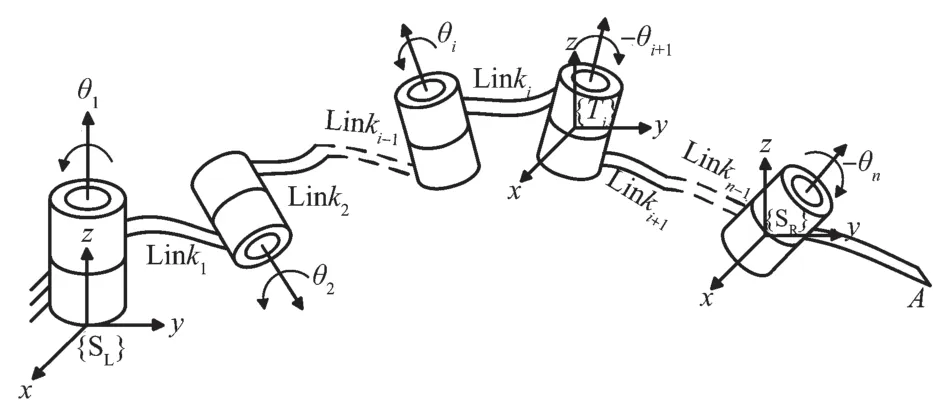
图2 子机器人R 基座标系未变换的情况Fig.2 R-based coordinate system of sub-robots without transformation
从图2 可以看出,QL表示一个i自由度机器人正向运动学,其基座标系与原n自由度机器人的惯性坐标系{SL}重合,其工具坐标系{Ti}则为gi(0)。QR则表示一个(n-i)自由度机器人正向运动学,其基坐标系{SR}位于关节n的原点,姿态与{SL}一致,其工具坐标系也为{Ti},该机器人各关节的旋转方向为负方向。式(5)右端整体可理解为QR所表示机器人的基座标系作变换后所得结果,如图3 所示。
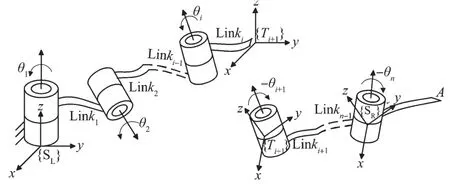
图3 子机器人变换后的情况Fig.3 Sub-robots under the transformation
综上所述,n自由度机器人可分离为两个低自由度的子机器人,上述理论同样适用含移动副的机器人。
即对n自由度机器人逆运动学求解,可理解为寻找使得两个子机器人重新结合为n自由度机器人的关节组合,可以重新结合的几何约束条件为两子机器人的工具坐标系位姿重合。该约束条件也是机器人分离的通用准则,尤其适用于分离点处的相邻关节轴轴线为共线、平行或垂直关系的机器人。
3 6R 机器人的结构分离
本节将以PUMA-560 为例,介绍6R 机器人的具体分离方法,为后面章节的逆运动学求解奠定基础。为方便描述,下文将关节1 至分离点组成的部分记为子机器人L,将分离点至关节6 组成的部分记为子机器人R。
3.1 正向运动学
图4 描述了PUMA-560 机器人在初始时各关节的螺旋轴。
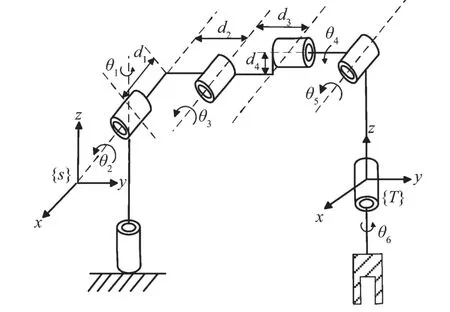
图4 PUMA-560 机器人的结构简图Fig.4 Structure schematic diagram of PUMA-560 robots
选择{S}作为惯性坐标系,{T}作为工具坐标系,{T}的原点与关节6 的原点重合。则机器人的初始位形为
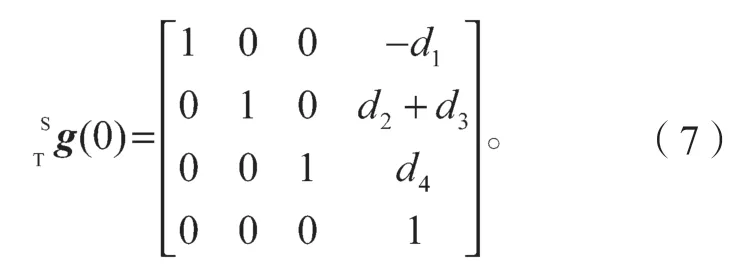
各关节螺旋轴如表1 所示。
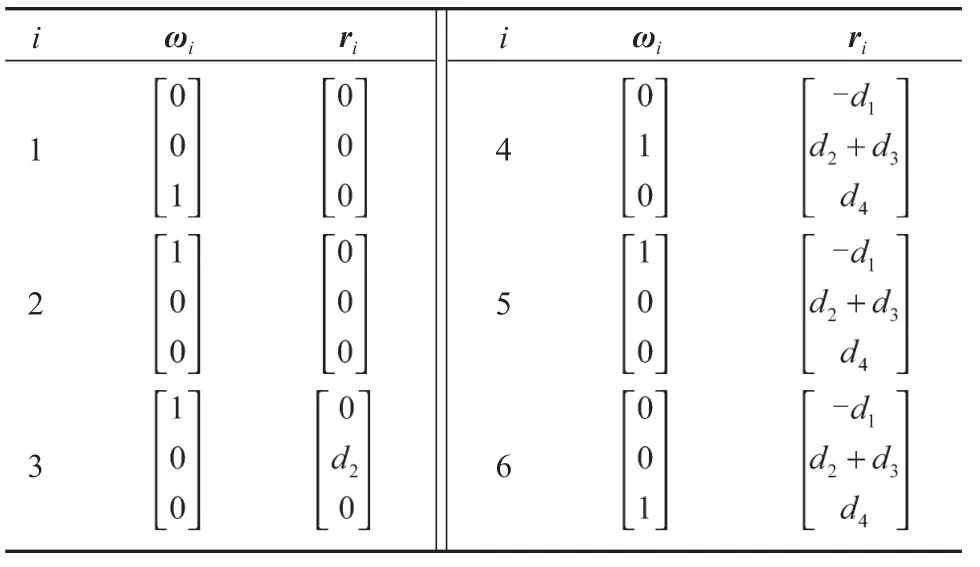
表1 PUMA-560 机器人的各关节螺旋轴Table 1 Spiral axes of each joint of PUMA-560 robots
PUMA-560 机器人的正向运动学公式为:
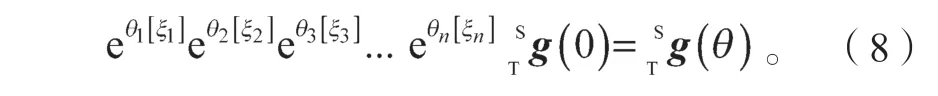
3.2 结构分离
已有文献多采用臂腕分离法[13]求6R 机器人的逆运动学解,即分为两个3R 部分,但在求逆解中θ5不能为0,否则会使关节4 和6 转轴共线,导致θ4和θ6无法进行求解。为避免奇异点,本文分离点选取关节4 的原点,将其分为4R 子机器人L 和2R 子机器人R。
由图3 可知,机器人关节1 至关节4 组成部分与3R 仿人臂结构类似,该类型机器人逆运动学已有完备的解法[14]。
由于此分离点相邻关节不满足图1 所示,因此子机器人末端工具坐标系需重新设定。图5 中原6 自由度机器人的工具坐标系变为子机器人R的基座标系,关节5 与关节6 轴线的单位向量不变,但旋转变为负方向,此时子机器人R 的基座标系还未变换。

图5 工具坐标系间的几何关系Fig.5 Geometric relations among tool coordinate systems
{TL}与{TR}分别表示两个子机器人的工具坐标系,二者的原点事实上是重合的,为便于观察,将{TL}向右进行平移。图中yL和yR与关节4 轴线重合,其方向不受θ4影响,xL和xR与关节5 轴线重合,其方向不受θ5影响;并且xL与yR共面且垂直,重合。{TR}和{TL}两个子机器人的工具坐标系重合,即TR=TL。故两个子机器人正向运动学可表示如下:
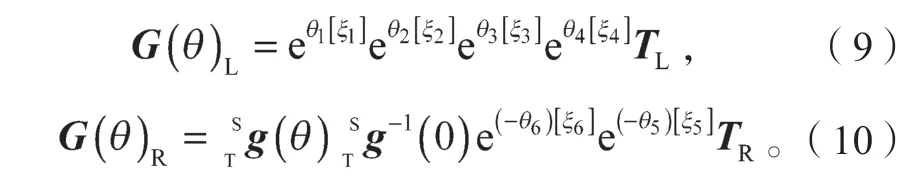
式(9)~(10)中:

将表1 中螺旋轴参数代入式(1)(2)(3)(9)(10),可得:

此时,两个子机器人可重新结合为后三关节轴线交于一点的6R 机器人的几何约束条件,变为{TL}与{TR}重合,xL与yR垂直,
4 求逆运动学解
4.1 θ1、θ2、θ3 和θ6 的求解
子机器人L 和子机器人R 可重构为6 自由度机器人应满足的第一个条件,是末端位置重合,故可令pL=pR,组成方程组:
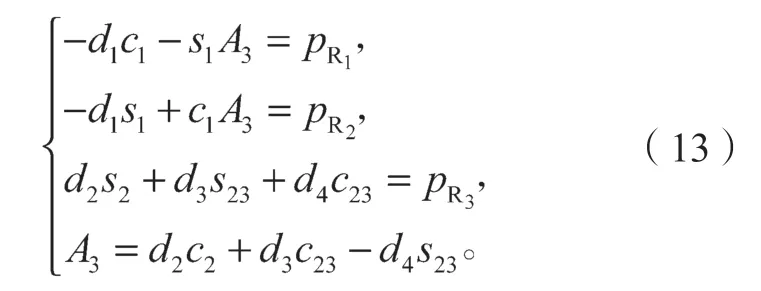
式(13) 中:sij、cij、si、ci分 别 表 示sin(θi+θj)、cos(θi+θj)、sinθi、cosθi;i,j为关节的序号;下文与此相同。
首先求式(13)的平方和,得:

式中:K1=±1;
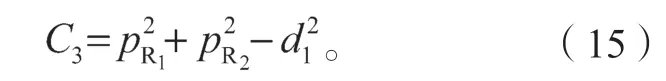
再将式(13)先平方后相加,得:
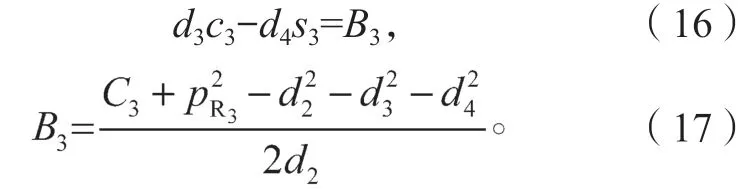
由上式得:

式中K2=±1。
由式(18)可得,当C3≥0 时θ3才有解。
确定θ3后,可通过计算式(13)(14)组成方程组,得到θ2:
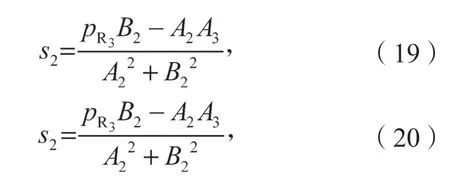

θ1可通过式(13)组成的方程组计算得出:

根据K1和K2的符号可知,θ?1、θ2和θ3可得到4组关于θ6的方程式。子机器人L 和子机器人R 可重构为6 自由度机器人应满足的第二个条件是轴线yL与轴线xR的夹角保持垂直,即|xR|=|yL|=1,可得:
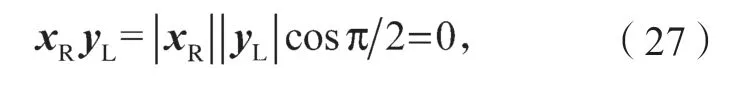
化简可得:

式中K3=±1。
由于向量yL与θ1、θ2和θ3有关,而xR只与θ6有关,故式(27)是一个仅与θ6有关的等式,根据θ1、θ2和θ3求解公式,可知θ6有8 个不同解。
4.2 θ4 和θ5 的求解
从图4 可以看出,一旦θ1、θ2、θ3和θ6确定后,即前面两个约束条件满足后,只要分别旋转θ4和θ5必然可以满足=,但是直接用该约束条件求θ4和θ5并不方便。
观察图4 可知,由于θ1、θ2、θ3和θ6确定后,向量yL与xR将保持不变,而yL与yR之间应该满足<yL,yR>=0,且此时向量yL与yR只有θ5一个未知量,故可由yLyR=1 求得θ5:
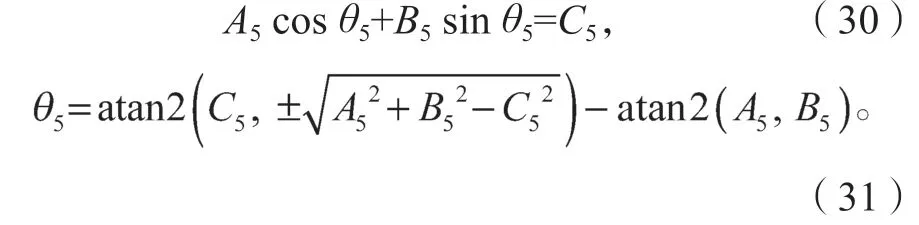
式(31)中根号部分事实上为0,θ5只有唯一解。以下给出证明。各轴的位置关系如图6 所示。
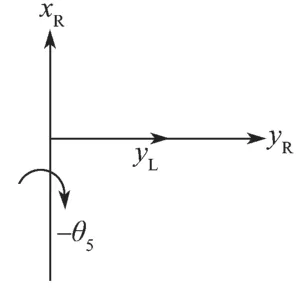
图6 各轴的位置关系Fig.6 Position relation of each axis
如图6 所示,θ5在旋转过程中,只有使得向量yR始终位于xR和yL所确定的平面内时才能满足约束条件。因此θ5在最小正周期内只有唯一解,式(31)可改写为

θ5求解后,再求θ4,使得<xL,xR>=0,同理可以求得θ4只有唯一解:
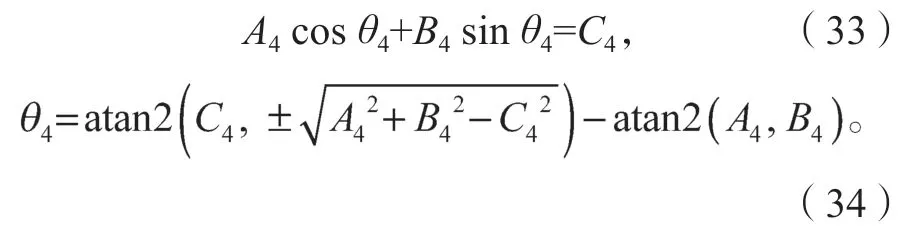
式(34)可改写为
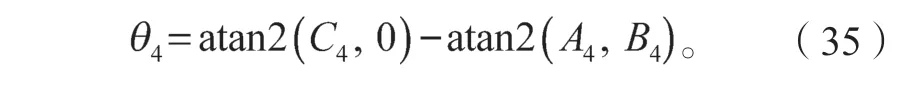
5 实验和验证
计算PUMA-560 机器人的逆运动学解,以验证算法的正确性。PUMA-560 机器人的结构参数如表2所示。

表2 PUMA-560 的D-H 参数Table 2 D-H parameters of PUMA-560
5.1 实验结果
在逆运动学算法的验证过程中,首先,在关节运动范围内给定一组初始的角度值;然后,根据POE公式计算目标的位姿;接下来根据得到的目标位姿和算法,确定每个关节的角度;在此之后,课题组再次使用获得的角度集来求解目标位姿,并且利用Matlab 对机器人的正、逆运动学进行计算。具体的验证过程如下:
1)给定目标位姿,PUMA-560 的杆长、角度值、弧度值。
杆长:d1=149.09 mm,d2=431.8 mm,d3=433.07 mm,d4=20.32 mm。
角度值:θ1=60°,θ2=50°,θ3=50°,θ4=60°,θ5=40°,θ6=-40°。
弧度值:θ1=1.047 19,θ2=0.872 78,θ3=0.872 66,θ4=1.047 19,θ5=0.698 13,θ6=-0.698 13。
2)求解正向运动学公式,得到目标位姿。
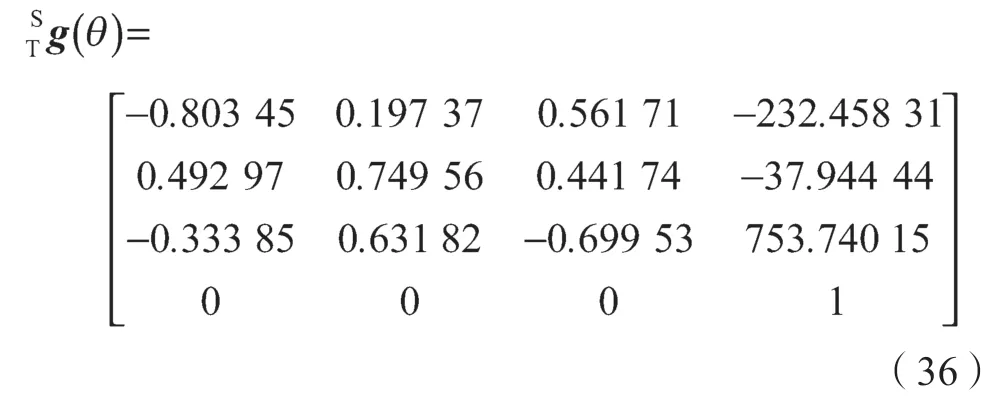
3)根据所提出的目标位姿和算法,求出所有逆运动学解,如表3 所示。
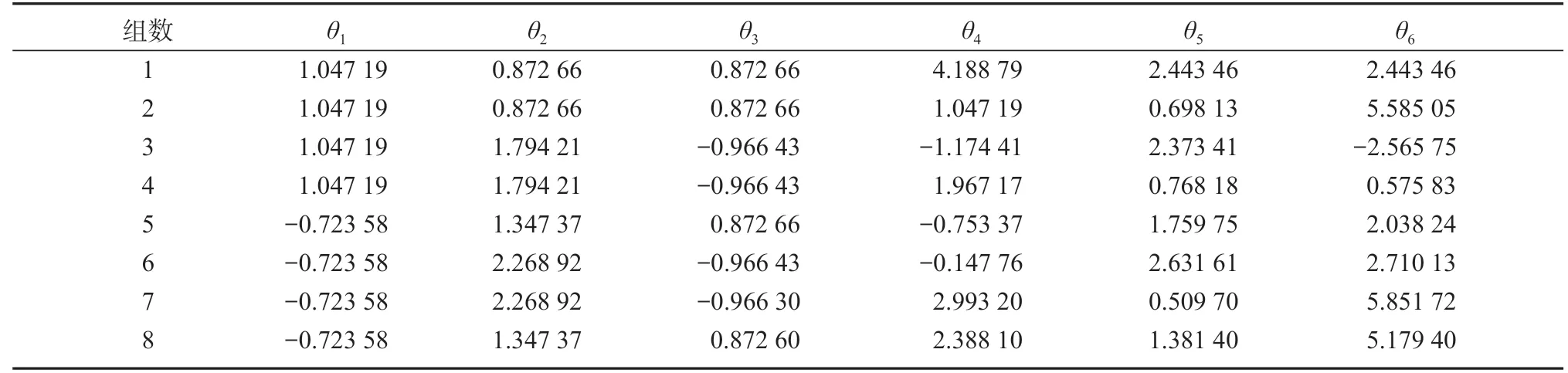
表3 目标位姿对应的逆解Table 3 Inverse solutions target pose correspondence
4)再次求正向运动学解,得到8 解的对应位姿。
5) 令En为目标位姿与实际位姿之间的误差,为第1 组的实际位姿, 根据计算步骤(2)和步骤(4)的误差,通过比较,可知第1 组解的误差最大,第5 组解的误差最小。
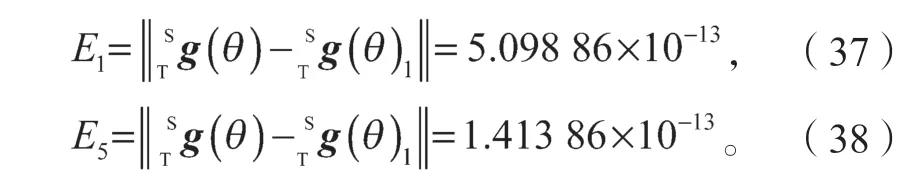
如式(37)和(38)所示,实际位姿与目标位姿间最大误差为10-13数量级,从而验证了算法的正确性和高精度性。
5.2 与D-H 坐标法比较
采用文献[6]中D-H坐标法和本文提出的新算法,分别对关节角进行1 000 次求逆运算,每次求50 组逆解的平均值,等距抽取其中的10 组用来比较。算法的计算软件为MatlabR2017b,PC 配置如下:处理器为Intel Core i7-8750H,CPU 速度为2.20 GHz,内存为8.00 GB。D-H 法与新算法求逆解耗时的比较如图7 所示。
从图7 中可看出,新算法较D-H 法在求逆运动学解的过程中速度有显著提高。D-H 法和新算法一次平均耗时分别为67.87,59.65 ms,新算法较D-H 法计算速度提高了12.1%。
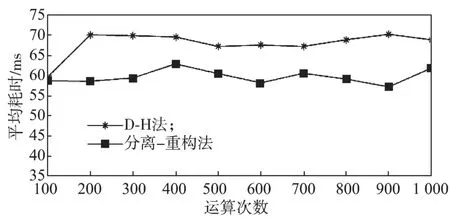
图7 D-H 法和新算法求逆解耗时比较Fig.7 Time consumption comparison between D-H method and the proposed algorithm
5.3 奇异性分析
文献[9]中针对后3 个关节轴线相交于一点的6R 机器人,利用D-H 法对PUMA-560 机器人进行正向运动学建模,采用臂腕分离法来求其逆解,即分为两个3R 部分,虽然该方法可避免矩阵求逆的运算,但在求逆解过程中,若θ5=0,则关节4 和6 转轴共线,导致θ4和θ6无法进行求解。利用本文的新算法,对上述情况进行分析:
1)给定位姿角度值:θ1=60°,θ2=50°,θ3=50°,θ4=60°,θ5=0°,θ6=-40°,求正向运动学公式,得到目标位姿:
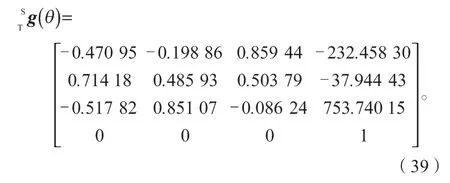
2)根据新算法和目标位姿,求出所有可能的关节角度。此时θ4、θ5、θ6会受到影响,而θ1、θ2、θ3不会受到任何影响,故可不详细列出。8 组θ4、θ5、θ6的逆运动学解如表4 所示。
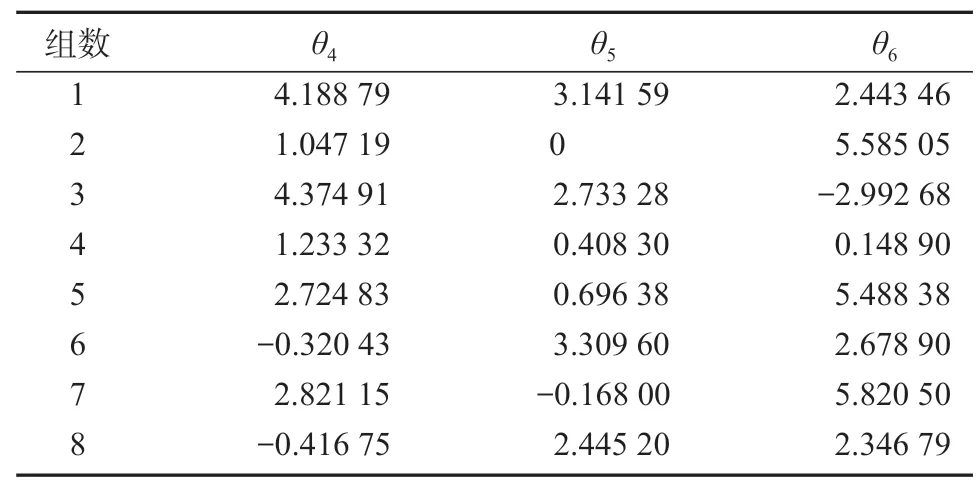
表4 8 组θ4、θ5、θ6 的逆运动学解Table 4 Solutions of eight groups of θ4,θ5 and θ6 inverse kinematics
由表4 可知,当θ5=0 时,利用本文的新算法可避免奇异点的影响,并且可求得8 组θ4、θ5、θ6的解。
5.4 结果讨论
在实验中确定了一组封闭解,即8 组解。因为PUMA-560 为后3 个关节为轴线交于一点的机器人,由新算法求得其逆运动学解如表3 所示,可知第5 组的误差最小。为验证新算法的正确性,将求得的8 组解与给定目标位姿比较,发现第1 组解与其误差最大,且实际位姿与目标位姿误差为10-13数量级,验证了算法的正确性和高精度性。
与文献[5]中封闭解法相比,新算法更具有理论推广性,同时也推导出其他关节角的具体求解方法。文献[6]中采用齐次坐标变换矩阵推导出逆运动学问题的解析解,其方法在计算逆向运动学的过程中需进行多次矩阵变换,导致运算速率较低。利用本文的新算法在求其逆解的过程,不仅避免奇异点,而且速度也有明显提高。与文献[9]的分离点相比,本文可避免奇异点,且计算过程中详细介绍了可分离条件,并用数学表达式证明了机器人的可分离性。
6 结论
本文利用螺旋理论建立了正向运动学模型,并且通过对机器人正向运动学指数积表达式变形,证明了任意机器人可分离为两个低自由度子机器人的可行性。提出后3 个关节轴线交于一点的6R 机器人分离点的选取及子机器人工具坐标系设定的方法:分离点应选取在可使子机器人具有完备逆解方法的位置;各子机器人工具坐标系的某一轴与对应子机器人末端关节轴线共线。以子机器人重新结合为6R 机器人的几何约束关系,推导出各个关节角求解公式,最后求得机器人逆运动学解;最终对PUMA-560 机器人进行验证,且实际位姿与目标位姿误差为10-13数量级,并在以下方面具有创新性:
与D-H 法求逆解速度相比,本文提出的方法对机器人结构重新解构,降低求解复杂度且几何意义明显,计算速度提高了12.1%;
本文选择的分离位置较传统臂腕分离法可避免奇异点的影响,解决了传统方法的弊端。
此外,本文提出的算法可被应用到其他类似构型的6R 串联机器人及其扩展构型逆解问题求解中,具有一定通用性。
