线控转向系统的自适应神经网络滑模控制

罗玉涛 郭海文

(华南理工大学 机械与汽车工程学院，广东 广州 510640)

汽车线控转向(SBW)系统取消了传统的转向盘到转向执行机构之间的机械连接，由电控系统直接进行转向控制，不仅有利于提高汽车的操纵稳定性和主动安全性，而且有利于推动汽车电动化和智能化的发展，是汽车转向技术的主要发展趋势[1]。

针对车轮转角控制的问题，目前已有多种控制方法应用于SBW系统，例如PID反馈控制[2- 3]和线性二次状态反馈控制[4]。但考虑系统不确定性和电机力矩扰动时，上述方法难以满足系统要求的鲁棒性。传统滑模控制(SMC)具有一定的抵抗外部干扰的能力[5- 7]，但在设计传统滑模控制器时，需要预先设定系统干扰的上界值，而且会存在明显的抖振现象。此外，有研究表明，可以通过结合智能控制和滑模控制理论来设计具有良好鲁棒性和稳定性的自适应车轮转角控制器[8- 11]。文献[8]基于传统滑模设计了具有在线训练自适应学习算法的二阶滑模控制器，能够实时估计系统干扰；文献[9] 提出了结合滑模控制和模型预测控制的容错滑模预测控制策略，使线控转向系统具有更好的鲁棒性和容错能力；文献[10]提出了一种自适应的终端滑模控制策略，该控制策略与传统滑模相比，不仅能保证系统的有限时间误差收敛性，而且对系统不确定性和力矩干扰具有更好的鲁棒性；文献[11]提出了一种自适应模糊滑模控制策略，利用模糊理论实时估计滑模控制器的切换增益，降低了传统滑模控制的保守性，并减少了车轮转角的抖振现象。

本文针对一种直驱式的线控转向系统构型，提出了基于径向基(RBF)神经网络滑模控制(RBFSMC)的车轮转角控制方法；通过建立SBW系统的数学模型，分析了系统的不确定性和电机的力矩扰动，并设计了SMC和RBFSMC控制器，再通过Matlab/Simulink和CarSim的联合仿真平台来验证RBFSMC的控制性能。

1 线控转向系统的构型

2 线控转向系统的数学建模

转向电机的动力学方程可以表示为[12]

(1)

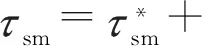
(2)

转向车轮的动力学方程可以表示为

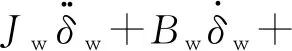
(3)

假设减速器的减速比为k，则

(4)

由式(1)、(3)、(4)可得SBW系统的动力学方程为

(5)

(6)

(7)

假设车辆的质心侧偏角和侧向加速度很小，则[14]

(8)

式中，β和γ分别为车辆质心侧偏角和横摆角速度，lf和lr分别为车轮的前、后轴距，vCG为车辆的质心速度。γ、δf和δr可以通过传感器测量，β则由整车单轨模型进行估算：

(9)

车轮与地面之间的摩擦力矩可以表示为

(10)

(11)

由式(7)可以确定回正力矩的上界为

(12)

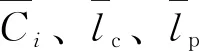
(13)

式中：id和iq为d-q轴的定子电流，可以由ia和ib通过Clark和Park变换计算得到；ud、uq、Ld和Lq分别为d-q轴的定子电压和电感；ψdm为d轴永磁体的磁链；R为定子绕组的电阻；ω为转子的电角速度；np为电机的极对数。

基于磁场定向矢量控制技术进行分析，在考虑电机的磁通谐波和电流谐波时，电机输出的实际力矩为

(14)

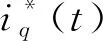
由式(14)可确定电机力矩扰动的上界为

(15)

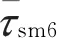
3 车轮转角控制器设计

3.1 传统滑模控制器设计

由式(5)可知，线控转向系统的动力学方程可以表示为

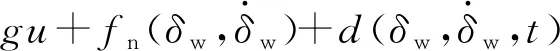
(16)

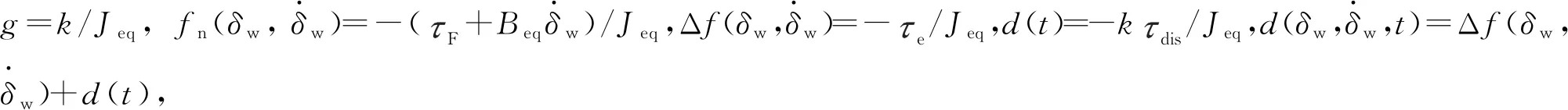
设期望车轮转角为δref，则转角误差为e=δref-δw。定义滑模面为

(17)

则控制律为

(18)

定义李雅普诺夫稳定性方程为L=s2/2，则

采用修正函数sat(s)代替sgn(s)，即

(19)

式中，Δ为边界层。sat(s)的作用是：在定义的边界层内，通过反馈控制来减小切换增益较大时滑模切换产生的抖振现象；在边界外，采用切换控制，以保证系统状态快速地趋近于滑模面。

3.2 径向基神经网络滑模控制器设计

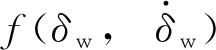
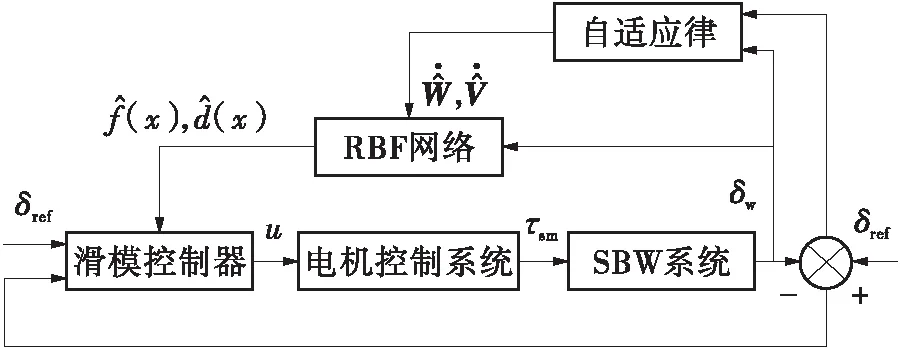
图2 RBFSMC控制框图

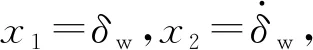
(20)

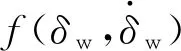
(21)

式中，hf(x)和hd(x)为RBF神经网络的高斯基函数。

控制律为

(22)

将式(22)代入式(16)和式(17)，得

(23)

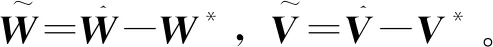
定义李雅普诺夫稳定性函数为

取自适应控制律为

(24)

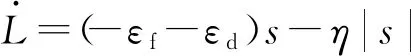
4 联合仿真试验与结果

本文基于Matlab/Simulink和CarSim平台进行联合仿真，其中选用CarSim中自带的微型轿车模型，通过屏蔽原有的机械转向系统来实现联合，整车模型参数如下：整车质量为800 kg，前轴距Lf为1.05 m，轴距L为1.6 m，机械拖距lc为0.018 m，气胎拖距lp为0.021 m，车速vCG为18 km/h。在车辆维持转向、连续转向和单/双移线工况下，对SMC和RBFSMC控制器的动态响应和稳态跟踪性能进行仿真分析。

采用图3所示的车辆前后轮侧偏刚度(Cf、Cr)和地面摩擦力矩系数(Fs)来模拟车辆行驶时系统不确定性引起的干扰；基于永磁同步电机建立磁场定向矢量控制的电机控制系统模型，以模拟电机输出的力矩扰动。

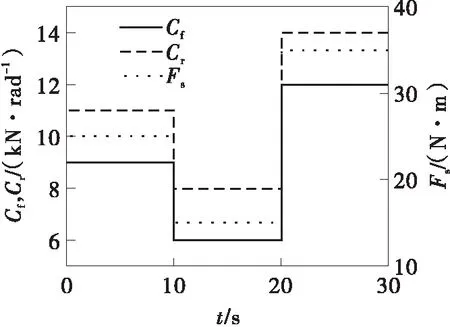
图3 车轮参数设置

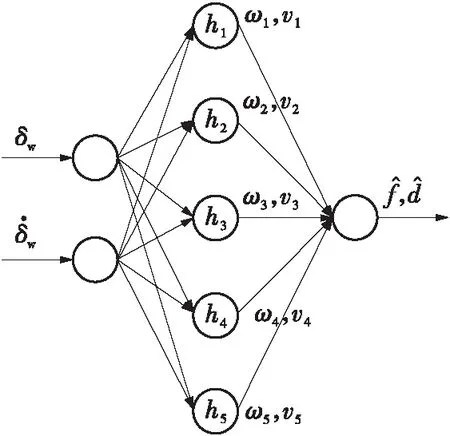
图4 RBF网络结构

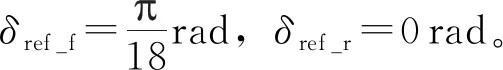
图5是维持转向工况下基于SMC的左前轮转角的仿真结果。图5(a)说明了车轮转角的快速响应和稳定维持的性能，在0.3 s时车轮转角能达到期望值，且存在-0.10°～0.25°的转角误差范围，当系统总干扰发生变化时，仍能够保持车轮转角维持的相对稳定。图5(b)表示由路面参数变化引起的系统不确定性和电机力矩扰动组成的系统总干扰，验证了通过定义车轮侧偏刚度和摩擦系数，以及建立电机控制系统模型来模拟系统总干扰的可行性。图5(c)表明，转向电机的控制力矩存在明显的抖振波动，不利于电机的实际控制。图5(d)表明，控制器的滑模函数可以维持在0位置附近，但波动范围较大。

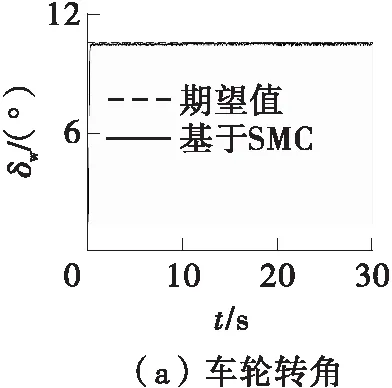
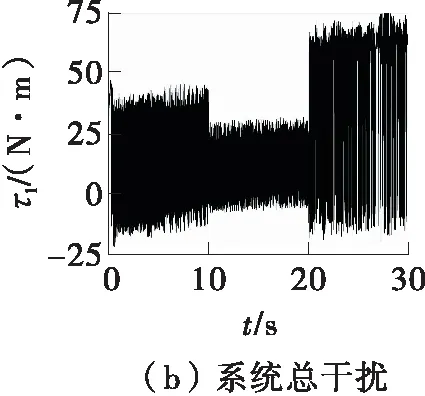
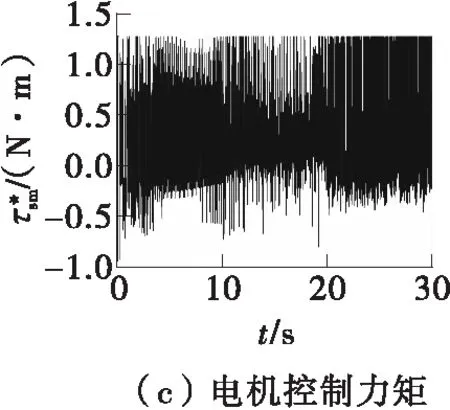
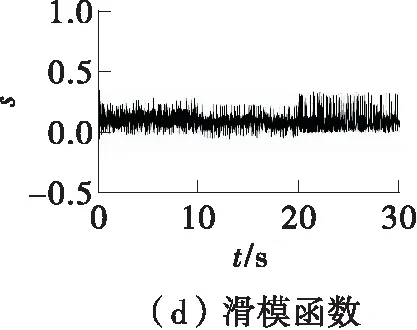
图5 维持转向工况下基于SMC的左前轮转角仿真结果

图6是维持转向工况下基于RBFSMC的左前轮转角仿真结果。图6(a)说明，在0.45 s时车轮转角能达到期望值，误差维持在-0.1°～0.1°，较SMC优化了42%。图6(c)表明，RBFSMC的转向电机的控制力矩较SMC具有更小的抖振现象，更有利于电机控制的实际应用。图6(d)表明，RBFSMC的滑模函数可以维持在理想0位置附近，较SMC的滑模函数波动范围更小，更稳定。

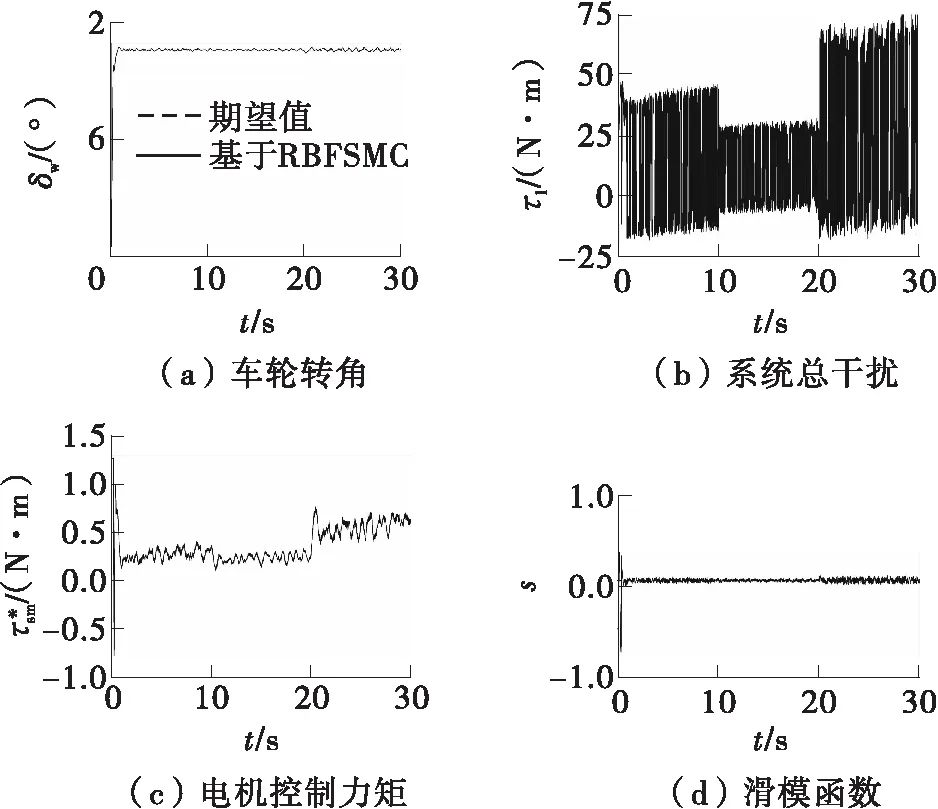
图6 维持转向工况下基于RBFSMC的左前轮转角仿真结果

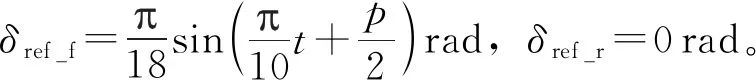
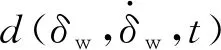
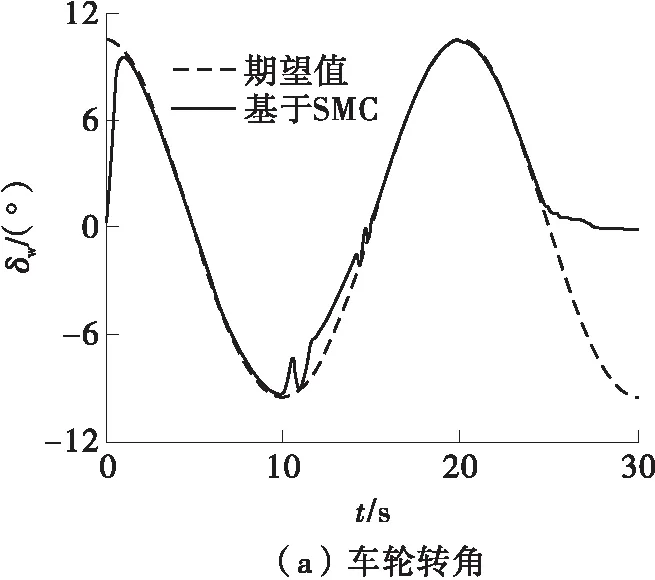
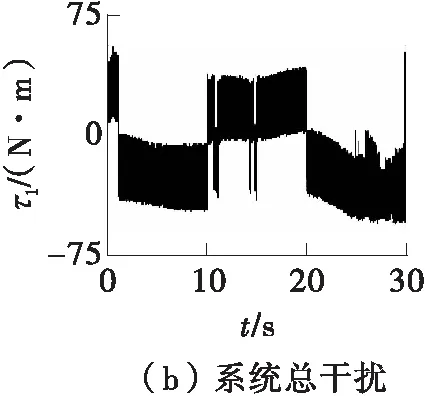
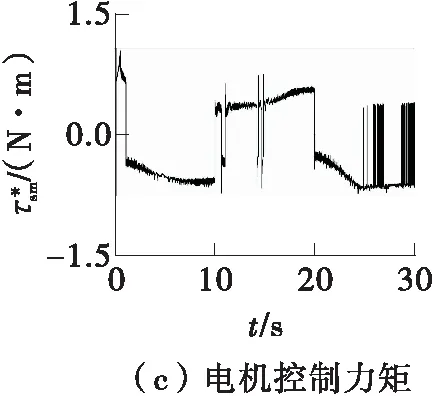
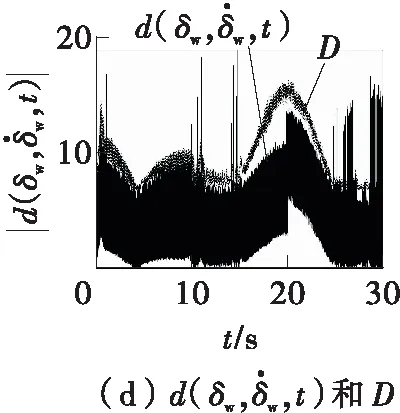
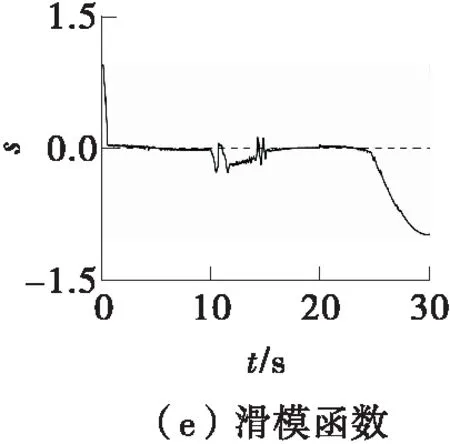
图7 连续转向工况下基于SMC的左前轮转角仿真结果

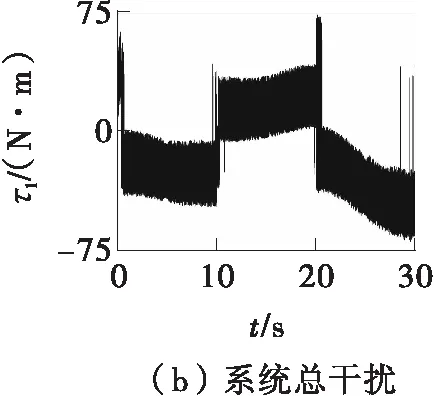
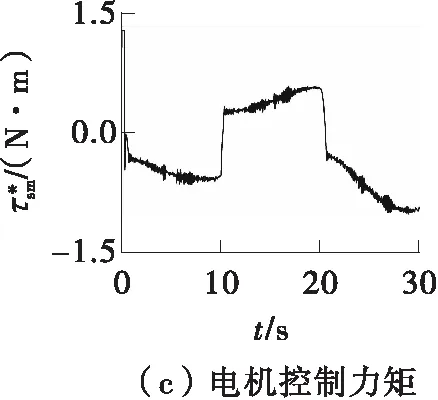
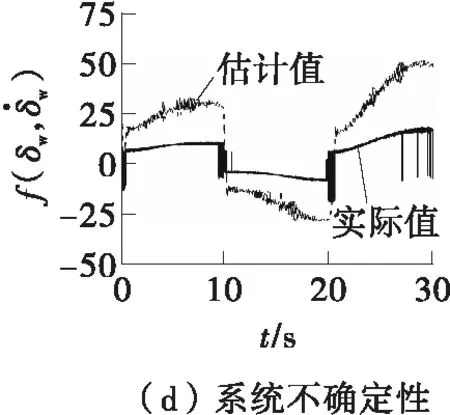
图8 连续转向工况下基于RBFSMC的左前轮转角仿真结果

工况3 为了进一步验证线控转向系统路径跟踪的性能，在CarSim中分别建立单移线和双移线工况，计算出理想路径跟踪时的车轮转角，并作为对SMC和RBFSMC仿真时输入的期望转角。

图9为单移线/双移线工况下基于SMC的左前轮转角仿真结果。从图中可知：在单/双移线工况下，SMC可以实现良好的轨迹跟踪，但SMC在跟踪期望转角时具有一定的误差，包括维持0°转角时-1°～1°范围的抖振和跟踪动态转角的误差；转向电机控制力矩存在较强的抖振现象，不利于电机的实际控制，其原因是当系统总干扰发生变化且切换项增益η取值较大时会引起明显的抖振；SMC的滑模函数虽然维持在滑模面的一定范围内，但明显的抖振现象说明SMC的稳定性较差，这说明开发更具自适应性和稳定性车轮转角控制器的必要性。

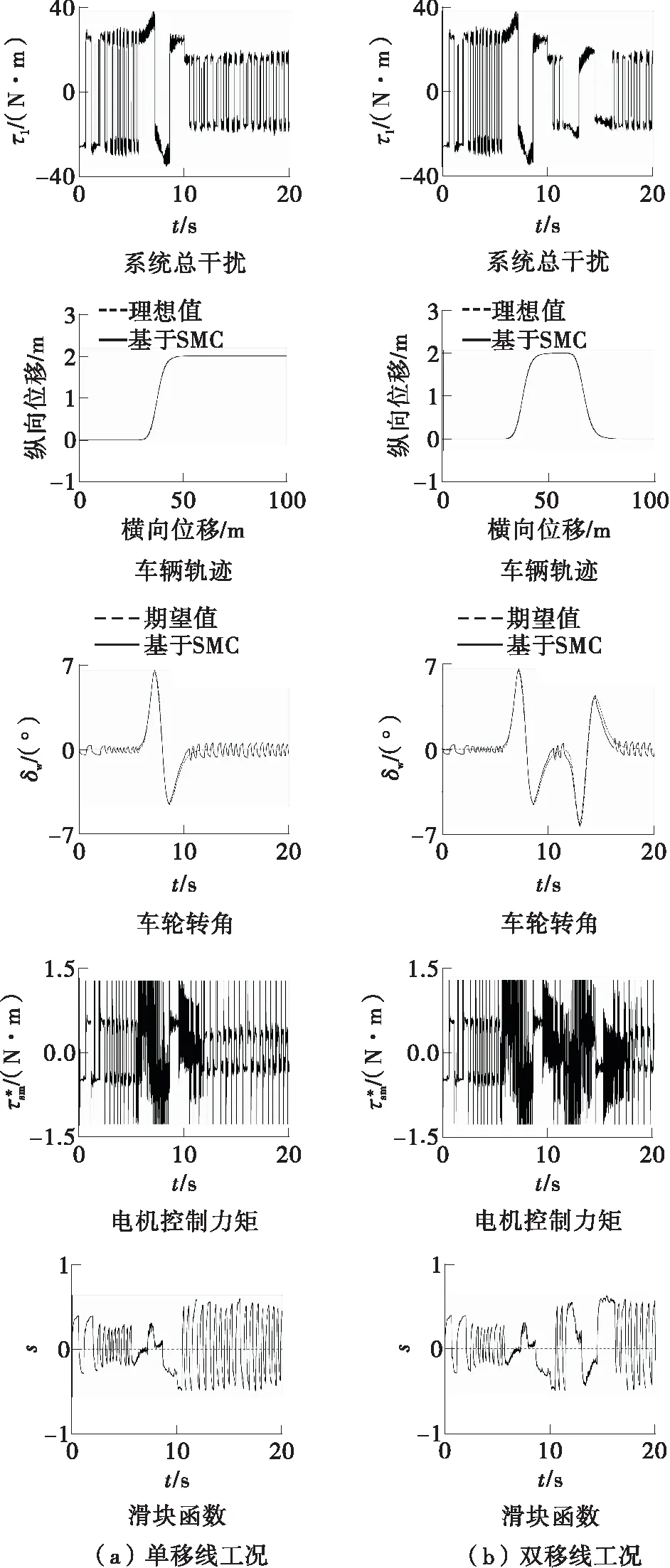
图9 单/双移线工况下基于SMC的左前轮转角仿真结果

图10为单/双移线工况下基于RBFSMC的左前轮转角仿真结果。比较图9、10可知：在单/双移线工况下，RBFSMC和SMC跟踪路径的性能差别不大，但RBFSMC的优势在于可以更稳定地维持0°车轮转角的跟踪，且在第10秒时车轮参数变化引起的转角波动更小；RBFSMC较SMC削弱了转向电机控制力矩的抖振现象，更符合电机控制的实际应用；RBFSMC的滑模函数基本上维持在滑模面附近且较SMC具有更小的波动范围和抖振现象，进一步说明了RBFSMC良好的稳定性和鲁棒性。

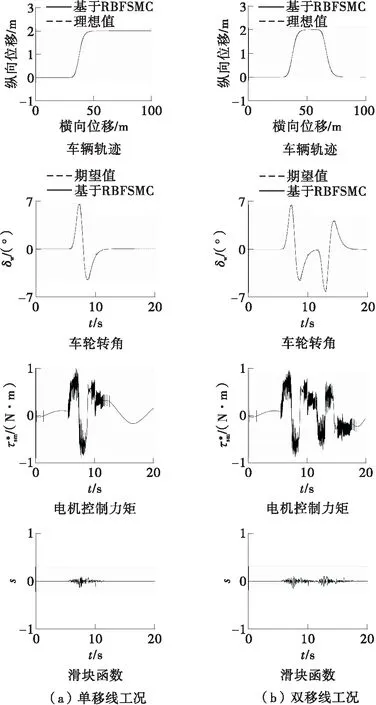
图10 单/双移线工况下基于RBFSMC的左前轮转角仿真结果

5 结论

本文基于一种直驱式的线控转向系统构型，提出了考虑系统干扰的自适应车轮转角控制方法。该方法先基于径向基神经网络对系统不确定性和转向电机力矩扰动进行实时估计，再结合滑模控制理论设计满足李雅普诺夫稳定性要求的车轮转角控制器。理论分析表明，RBFSMC提高线控转向系统性能的原因在于，采用了具有强非线性的神经网络对系统中存在的不确定性和干扰进行实时估计，从而保证转角控制器始终满足李雅普诺夫的稳定性要求，故较控制器参数固定的SMC具有更好的转角控制性能和稳定性。Matlab/Simulink和CarSim的联合仿真结果表明：在车辆维持转向和连续转向工况下，RBFSMC具有比SMC更好的转角响应和跟踪性能，具有良好的自适应性；在单移线/双移线工况下，RBFSMC不仅能够维持0°车轮转角，而且能够快速稳定地跟踪动态的车轮转角。因此，RBFSMC比SMC能更有效地削弱干扰对系统产生的影响，具有更好的鲁棒性和稳定性。