基于自适应滤波器的无人驾驶汽车速度估计

张家旭 王晨 王欣志 赵健†

(1.吉林大学 汽车仿真与控制国家重点实验室，吉林 长春 130022；2.中国第一汽车集团有限公司 智能网联研发院，吉林 长春 130011)

无人驾驶汽车被认为是解决城市交通拥堵问题的重要手段之一，而通过软测量技术准确实时地获取无人驾驶汽车速度信息是无人驾驶汽车实现容错控制、提升自身安全性的重要保证，也是解决传感器直接测量方式导致的无人驾驶汽车容错控制可靠性差、成本高等问题的有效手段[1- 2]。因此，深入研究开发无人驾驶汽车速度软测量技术对提前布局无人驾驶汽车领域具有重要的战略意义。

无人驾驶汽车速度估计方法按名义模型类别可大致划分为基于动力学模型的估计方法、基于运动学模型的估计方法和基于动力学与运动学模型的估计方法。文献[3]基于线性轮胎模型建立了包含汽车纵向速度动态、侧向速度动态和横摆角速度动态的非线性动力学模型，并采用前向欧拉离散化方法将其转化为容积卡尔曼滤波器的名义模型，实现了汽车速度的实时估计。由于线性轮胎模型无法准确描述轮胎极限工况下呈现出的强耦合和非线性特征，导致文献[3]提出的汽车速度估计方法在极限工况下存在较大的估计误差。为此，文献[4]基于魔术公式轮胎模型建立了包含汽车纵向速度动态、侧向速度动态、横摆角速度动态和4个车轮角速度动态的非线性动力学模型，并采用泰勒-李级数离散化方法将其转化为包含系统噪声统计特性的名义模型，随后利用无迹卡尔曼滤波器对汽车速度进行估计。无迹卡尔曼滤波器通常需要已知系统噪声统计特性才能实现汽车速度的高精度估计，而实际工程应用中难以准确获得系统的噪声统计特性。为此，文献[5]融合高滤波精度的平方根容积卡尔曼滤波器和强鲁棒性的平方根容积卡尔曼有限脉冲滤波器的优势，提出了汽车速度混合卡尔曼滤波器：在系统噪声统计特性估计误差较小时，采用平方根容积卡尔曼滤波器对汽车速度进行实时估计；在系统噪声统计特性估计误差较大时，采用平方根容积卡尔曼有限脉冲滤波器对汽车速度进行实时估计。由于文献[4- 5]采用的名义模型维数较大，故提出的汽车速度估计器具有较高的复杂度。为此，文献[6]解耦车身动态和车轮动态，建立了分层结构的汽车速度估计器：在车轮动态层面，利用高阶滑模观测器实时估计汽车轮胎力；在车身动态层面，将车轮动态层面估计的汽车轮胎力作为输入，利用超螺旋滑模观测器对汽车速度进行估计。文献[7]也采用该分层结构设计了汽车速度估计器，在车轮动态层面和车身动态层面，分别采用滑模观测器和扩展卡尔曼滤波器实时估计汽车轮胎力和速度。

相对于基于动力学模型的估计方法，基于运动学模型的估计方法和基于动力学与运动学模型的估计方法可进一步降低汽车速度估计器的复杂度。文献[8]采用汽车横摆角速度、纵向速度和侧向加速度描述汽车质心侧偏角变化率，并通过积分运算直接获取汽车质心侧偏角，进而利用汽车质心侧偏角定义式推导出汽车侧向速度。但积分运算通常会产生累积误差，影响汽车侧向速度的估计精度。文献[9]将汽车横摆角速度作为调度参数，建立了线性时变参数汽车运动学模型，并采用鲁棒H∞滤波方法实现了汽车速度的实时估计。文献[10]利用传感器测量的轮胎纵向力和侧向力建立了包含汽车纵向速度和侧向速度的运动学模型，并采用卡尔曼滤波器实现了汽车纵向速度和侧向速度的实时估计。文献[11]利用传感器测量的轮胎侧向力建立了包含汽车运动学和动力学特性混合名义模型，并采用扩展卡尔曼滤波器实现了汽车速度的实时估计。文献[10- 11]均将轮胎力作为可测量状态信息，但鉴于轮胎力传感器的装配位置和使用环境约束，难于满足无人驾驶汽车容错控制需求。同时，高精准度和高鲁棒性的无人驾驶汽车定位技术是自动驾驶领域的基础技术之一，但上述研究成果均未能充分利用无人驾驶汽车的定位信息进行速度估计。

有鉴于此，本文充分利用无人驾驶汽车的定位信息，建立包含汽车运动学和动力学特性的名义模型，并采用前向欧拉离散化方法将其转化为包含系统过程噪声和观测噪声统计特性的状态空间名义模型；然后采用一系列典型值描述系统未知的过程噪声和观测噪声统计特性，得到一系列包含不同系统过程噪声和观测噪声统计特性的状态空间名义模型，并针对每一个状态空间名义模型，分别采用无迹卡尔曼滤波器(UKF)对无人驾驶汽车的速度进行实时估计，通过交互式多模型(IMM)算法平滑融合无迹卡尔曼滤波器的输出，由此得到对系统过程噪声和观测噪声统计特性具有自适应能力的交互式多模型无迹卡尔曼滤波器(IMM-UKF)；最后，采用实车试验采集的数据离线验证所提出的无人驾驶汽车速度估计方法的可行性和有效性。

1 数学模型

轮胎力是驱动无人驾驶汽车速度变化的主要外力来源，但轮胎力通常呈现出强耦合和非线性特征，使得基于轮胎力描述模型设计的无人驾驶汽车速度观测器的结构复杂，运算效率低。为此，本文利用已知的无人驾驶汽车定位信息建立汽车运动学和动力学模型，并将其作为无人驾驶汽车速度估计器的名义模型。如图1所示，建立地面坐标系OXYZ和车身坐标系OVXVYVZV，无人驾驶汽车运动学和动力学方程可以描述为[12]

(1)

式中，X和Y分别为无人驾驶汽车质心点的纵向坐标和侧向坐标，φ和γ分别为无人驾驶汽车的横摆角和横摆角速度，vx、vy、ax和ay分别为无人驾驶汽车的纵向速度、侧向速度、纵向加速度和侧向加速度。

选择无人驾驶汽车纵向速度、侧向速度和横摆角作为系统状态向量，即

x=[vxvyφ]T

(2)

假设无人驾驶汽车纵向坐标、侧向坐标和横摆

图1 无人驾驶汽车模型

角为已知量。因此，本文选择无人驾驶汽车质心点的纵向坐标增量、侧向坐标增量和横摆角作为系统观测向量，即

(3)

用于实时测量汽车纵向加速度、侧向加速度和横摆角速度的Yaw-G传感器是无人驾驶汽车的标准配置[8]。因此，本文选择无人驾驶汽车纵向加速度、侧向加速度和横摆角速度作为系统输入向量:

(4)

基于式(2)-(4)描述的系统状态向量、观测向量和输入向量，利用前向欧拉法将式(1)离散化为包含零均值高斯过程白噪声wk和零均值高斯观测白噪声vk的汽车状态方程和观测方程

(5)

(6)

(7)

式中，T为采样时间。

2 交互式多模型无迹卡尔曼滤波器

无迹卡尔曼滤波器利用Unscented变换代替传统扩展卡尔曼滤波器的雅克比矩阵运算，在已知系统过程噪声和观测噪声统计特性的前提下可以获得更高的估计精度[13- 15]。但在实际工程应用中，难于精确获得系统过程噪声和观测噪声的统计特性，从而导致无迹卡尔曼滤波器的估计精度降低。同时，研究表明：在零均值高斯过程白噪声的协方差Q保持不变时，增加零均值高斯观测白噪声的协方差R可以减小高斯过程白噪声对滤波算法估计精度的影响，但会导致滤波算法收敛速度降低；在零均值高斯观测白噪声的协方差R保持不变时，增加零均值高斯过程白噪声的协方差Q可以减少滤波算法的时间延迟，但会增加高斯观测白噪声对滤波算法估计精度的影响。为此，本文针对3个包含不同系统过程噪声和观测噪声统计特性的状态空间名义模型，分别并行运行3个无迹卡尔曼滤波器，并采用交互式多模型算法融合3个无迹卡尔曼滤波器的输出，由此得到对系统过程噪声和观测噪声统计特性具有自适应能力的交互式多模型无迹卡尔曼滤波器(其总体架构如图2所示)，包括输入交互模块、UKF滤波器1、UKF滤波器2、UKF滤波器3、概率更新模块和输出融合模块。

图2 交互式多模型无迹卡尔曼滤波器总体架构

如图2所示，UKF滤波器1、UKF滤波器2和UKF滤波器3的零均值高斯过程白噪声的协方差Q和零均值高斯观测白噪声的协方差R分别设置为较小值、适中值和较大值，并假设S={S1,S2,S3}为UKF滤波器1、UKF滤波器2和UKF滤波器3构成的集合，具体的滤波过程如下：

(8)

(9)

(10)

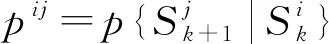
(11)

(12)

(13)

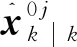
(14)

(15)

(3)概率更新模块利用UKF滤波器1、UKF滤波器2和UKF滤波器3的残差信息，计算输出k+1时刻元素Sj的条件概率，即

(16)

(17)

(18)

(19)

3 实车试验验证

本文首先使用图3所示的车辆进行实车试验，并利用Racelogic公司的VBOX测试系统记录车辆位置、速度、加速度和横摆角等信息，并同步记录CAN总线输出的方向盘转角。随后，采用Matlab软件的S-函数实现基于交互式多模型无迹卡尔曼滤波器的无人驾驶汽车速度估计方法，将实车试验记录的数据作为输入信息，以验证本文所提出估计方法的可行性和有效性。

图3 试验车辆

在试验过程中，UKF滤波器1、UKF滤波器2、UKF滤波器3的零均值高斯过程白噪声的协方差和零均值高斯观测白噪声的协方差分别设置为Q1=R1=diag{0.000 1,0.000 1,0.000 1}，Q2=R2=diag{0.001,0.001,0.001}，Q3=R3=diag{0.01,0.01,0.01}。3个UKF滤波器的转移概率构成的转移矩阵设置为

3.1 调幅正弦转向工况

在调幅正弦转向工况中，初始车速和路面附着系数分别设置为33.33 m/s和1，无人驾驶汽车的前轮转向角输入如图4(a)所示，纵向加速度、侧向加速度和横摆角速度如图4(b)所示，基于本文提出的IMM-UKF和基于UKF估计得到的无人驾驶汽车纵向速度、侧向速度和横摆角如图4(c)-4(e)所示。

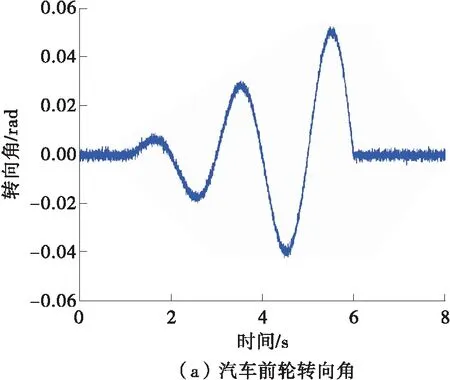
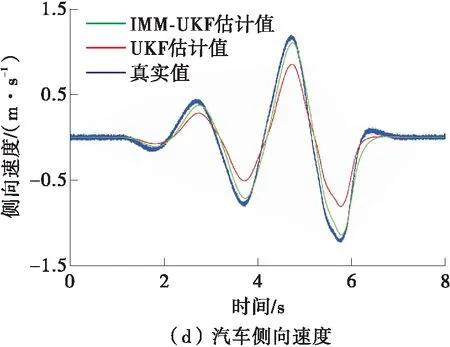
图4 调幅正弦转向工况下两种方法的仿真结果

由图4(b)可知，调幅正弦转向工况使无人驾驶汽车由线性工作区域逐渐过渡到非线性工作区域。由图4(e)可知，基于UKF和基于IMM-UKF的无人驾驶汽车速度估计方法对无人驾驶汽车横摆角均具有较高的估计精度。由图4(c)、4(d)可知，相对于基于UKF的无人驾驶汽车速度估计方法得到的汽车纵向速度和侧向速度，基于IMM-UKF的无人驾驶汽车速度估计方法在无人驾驶汽车线性工作区域和非线性工作区域均呈现出更高的估计精度。采用文献[17]的残差计算方法得到基于UKF和基于IMM-UKF的无人驾驶汽车速度估计方法的残差,如表1所示。量化结果表明：基于IMM-UKF的无人驾驶汽车速度估计方法对汽车纵向速度和侧向速度的估计精度更高。

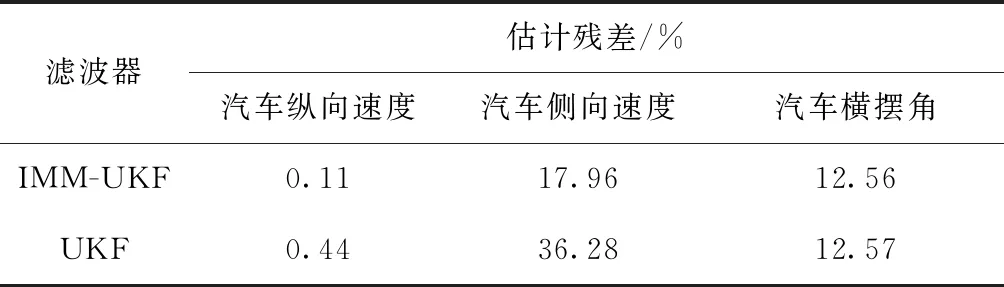
表1 调幅正弦转向工况下两种方法的估计残差

3.2 正弦延迟工况

在正弦延迟工况中，初始车速和路面附着系数分别设置为22.22 m/s和1，无人驾驶汽车前轮转向角输入如图5(a)所示，无人驾驶汽车的纵向、侧向加速度和横摆角速度如图5(b)所示，基于本文提出的IMM-UKF和基于UKF估计得到的无人驾驶汽车纵向速度、侧向速度和横摆角如图5(c)-5(e)所示。由图5(b)可知，正弦延迟工况为无人驾驶汽车的极限行驶工况。由图5(c)-5(e)可知，相对于基于UKF的无人驾驶汽车速度估计

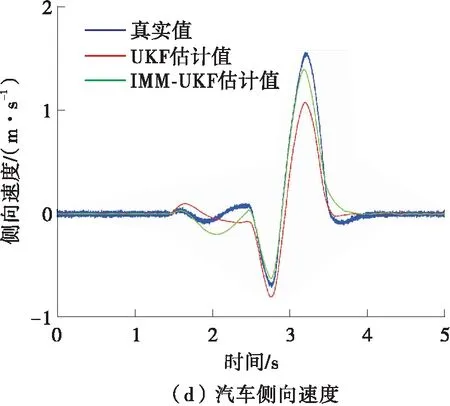
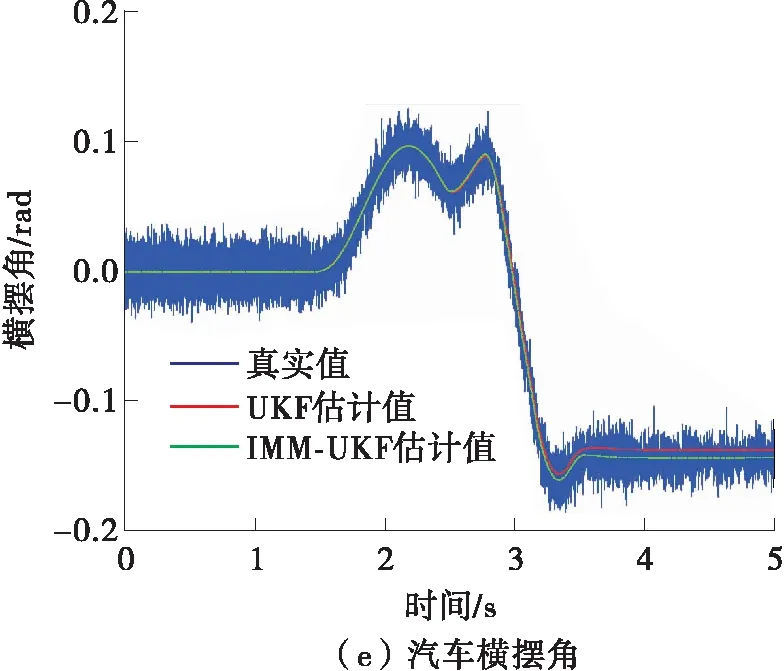
图5 正弦延迟工况下两种方法的仿真结果

方法，基于IMM-UKF的无人驾驶汽车速度估计方法具有更高的动态估计精度和稳态估计精度。采用文献[17]的残差计算方法得到基于UKF和基于IMM-UKF的无人驾驶汽车速度估计方法的残差,如表2所示。量化结果表明：基于IMM-UKF的无人驾驶汽车速度估计方法对汽车纵向速度、侧向速度和横摆角的估计精度更高。

表2 正弦延迟工况下两种方法的估计残差

4 结论

本文基于无人驾驶汽车定位信息建立了包含汽车运动学和动力学特性的名义模型，并采用前向欧拉离散化方法将其转化为包含系统过程噪声和观测噪声统计特性的状态空间名义模型；然后采用一系列典型值描述系统未知的过程噪声和观测噪声统计特性，得到一系列包含不同系统过程噪声和观测噪声统计特性的状态空间名义模型，并针对每个状态空间名义模型，分别采用无迹卡尔曼滤波器对无人驾驶汽车的速度进行实时估计，通过交互式多模型算法平滑融合无迹卡尔曼滤波器的输出，得到对系统过程噪声和观测噪声统计特性具有自适应能力的交互式多模型无迹卡尔曼滤波器；最后利用实车试验采集的数据离线验证了本文所提出的无人驾驶汽车速度估计方法的可行性和有效性。试验结果表明：基于本文提出的IMM-UKF的无人驾驶汽车速度估计方法比基于UKF的方法具有更高的估计精度；本文提出的无人驾驶汽车速度估计方法对汽车纵向速度的估计精度是传统无迹卡尔曼滤波方法的4倍，对汽车侧向速度的估计精度是传统无迹卡尔曼滤波方法的1.5倍，使得无人驾驶汽车可以利用该方法得到的车速信息实现容错控制，提升自身安全性。