切削过程中剪切区微观组织演化的预测模型

周滔 何林,2† 田鹏飞 杜飞龙,3 吴锦行

(1.贵州大学 机械工程学院，贵州 贵阳 550025；2.六盘水师范学院 矿业与土木工程学院，贵州 六盘水 553000；3.贵州大学 现代制造技术教育部重点实验室，贵州 贵阳 550025)

金属的切削过程通常会产生机械载荷和热载荷，并伴随着材料的微观组织变化。早期的解析性切削模型[1- 3]没有考虑材料微观组织性能的影响。如Merchant[1]认为主剪切区中的剪应力为常数。Lee等[3]提出了基于滑移线场理论的求解方法。Oxley等[4]考虑应变、应变速率和温度敏感性，提出了剪切区热力学分析模型。然而，这些分析方法未能反映出工件材料的复杂变形行为，尤其是微观组织演化过程的影响很少被考虑。

在材料切削过程建模时，材料模型中相关的微尺度变形机制考虑越多，在有效范围内的预测越准确。Atmani等[5]提出了切削过程多物理模型，发现基于力学阈值的应力模型预测的切削力在低速切削时更加精确。Pan等[6]将晶粒生长和材料软化的影响嵌入到Johnson-Cook(J-C)流动应力方程中，结合Oxley模型[4]迭代计算切削力，和传统的J-C材料模型相比，预测的切削力与实验值更接近。除此之外，基于物理本质的材料模型在捕捉切削过程中潜在的微尺度变形机制方面,已经被认为是一种有效的手段。Ding等[7]通过考虑相变和晶粒细化的多物理模型来预测微观组织的变化，认为中低速切削产生的晶粒细化是由材料严重塑性变形导致，高速下的白层是由热驱动相变和严重塑性变形引起的晶粒细化所致，通过切削力和残余应力的预测进一步验证了模型更加有效。Liu等[8]考虑微观结构的演化过程以及位错阻力变形机制，提出了适用于高速切削加工的统一材料模型，并利用该模型分析了变形场参数的演化过程，得到了切削诱导微观组织与变形场参数的关系图。Shen等[9]基于位错密度的材料模型研究了AZ31B镁合金在多道次低温切削加工过程中的纳米晶粒细化机制。

以上研究在考虑到材料微观组织演化对材料力学行为的影响时，大多是基于有限元法(FEM)来实现机械加工中的微观组织演化预测。相对于FEM的加工过程建模，解析模型提供了一种更简便的实现方法，具有较高的计算效率，可以显式地计算加工过程中材料的热力耦合响应。为此，本文基于非等距剪切区应变场、温度场和位错密度材料模型，构建了一种剪切区微观组织演化解析模型(UDS-DD)，并用来预测直角切削无氧铜(OFHC Cu)、铝合金(Al 6061 T6)的切削力和切屑内晶粒尺寸，通过实验验证该解析模型的有效性。

1 微观组织演化模型

切削过程中主剪切区(PSZ)发生的剪切变形是一种强塑性变形(SPD)[10- 11]，而SPD过程中晶粒细化是由于大塑性应变引发的位错运动而形成新晶界的结果[7]，这可能促进了切屑形成过程中晶粒的细化。因此，本研究采用基于位错密度的材料模型来模拟切屑的晶粒细化过程，切屑形成机理示意图如图1所示。

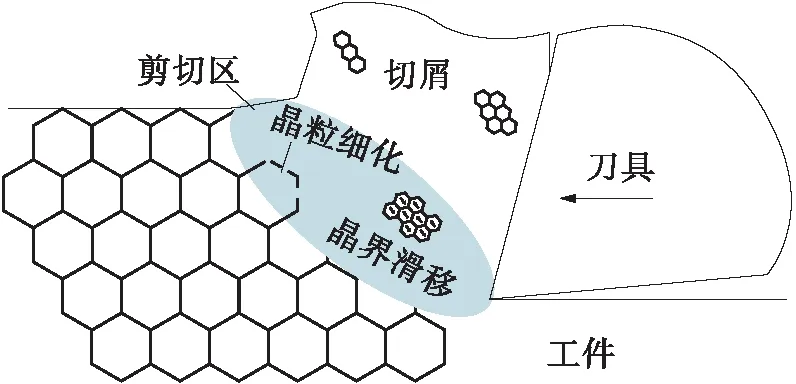
图1 剪切区晶粒细化示意图

为了预测切削过程中切屑的微观组织演变，引入位错密度模型[12]，该模型由不同类型的位错密度组成：胞内位错密度(ρc)和胞壁位错密度(ρw)，胞壁位错密度又被进一步分为统计位错密度(ρws)和几何必须位错密度(ρwg)。位错密度的演化遵循不同的计算方法：

(1)

(2)

(3)

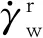
(4)

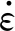
(5)

胞壁位错体积分数f、位错总密度ρtot和晶粒尺寸d的表达式如下：

f=f+(f0-f

(6)

ρtot=f(ρws+ρwg)+(1-f)ρc

(7)

(8)

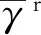
2 基于位错密度的材料模型

在本文建立的解析模型中，通过位错密度来计算金属材料的本构关系，以此确定力学行为，等效应力为

σ=σ1+σ2

(9)

(10)

(11)

(12)

(13)

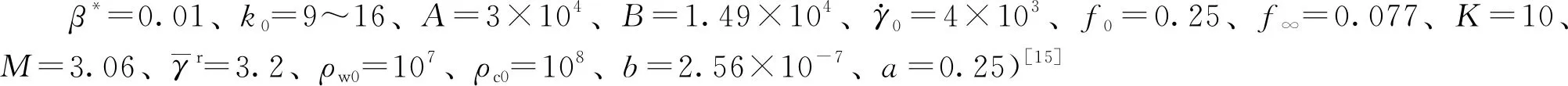
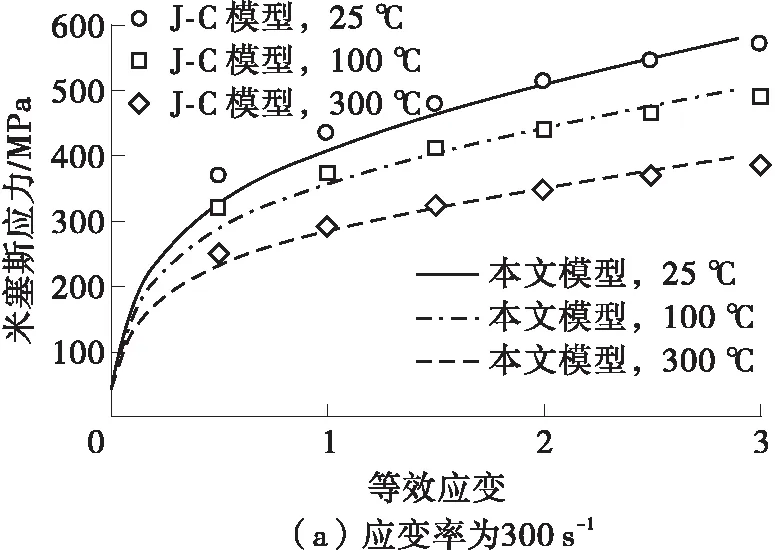
图2 基于位错密度的OFHC Cu应力-应变曲线

3 直角切削主剪切区建模

用于分析速度和力学关系的主剪切区模型有单剪切面模型[1]、平行面剪切区模型[4]和扇形剪切区模型[17]。这些模型均取得了较好的预测效果。Tounsi等[18]基于平行面剪切区模型[4]，提出了主剪切区的非等距剪切区模型，该模型显示剪切区被分为窄区和宽区，Astakhov等[19]通过实验验证了剪切区的非等距分布特征。非等距剪切区模型示意图如图3所示，主剪切区是宽度为h的平直带状区域，AB为主剪切面，CD与EF两边界相互平行，图3(a)中γ0为刀具前角，t1为切削厚度，φ为给定切削参数和刀具几何条件下的剪切角，通过φ与工件坐标系xoy的关系，可得到图3(b)所示的剪切区坐标系xsoys，以此分析剪切区应变场和温度场的变化过程，vc、vs和v分别为切屑流动速度、剪切面材料流动速度和切削速度，Fs为AB上的剪应力。

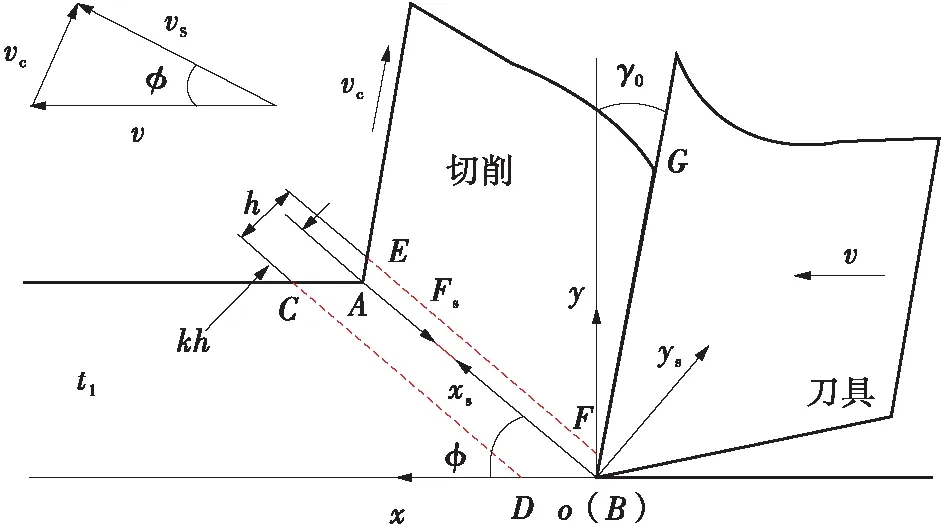
(a)工件坐标系

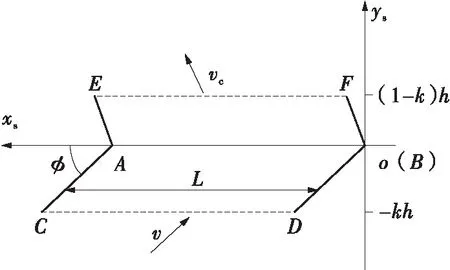
(b)剪切区坐标系

从图3的几何关系可以得到剪切面长度L和切削厚度t1的关系如下：

L=t1/sinφ

(14)

目前很少有分析方法能够仅使用材料属性和切削参数来预测φ。Toropov等[20]提出了一种基于实验和理论的简化滑移线模型，利用工作材料的热力属性和给定的切削条件,快速确定直角连续切削的剪切角，方程如下：

(15)

由于速度场必须满足塑性不可压缩性的假设，因此得到如下方程：

(16)

根据周芳娟[21]的研究，剪切角和切削速度为定值，剪切区的材料流动速度在ys方向上的分量为一常数：vys=vsinφ。Grzesik[22]研究表明，剪切区厚度值h会随着切削厚度和剪切角的变化而改变，关系式为h=t1/(10 sinφ)。考虑到切削参数对加工过程的影响，本文在计算剪切区厚度h时，采用Grzesik的计算公式。得到剪切区材料流动在ys方向上的速度和厚度之后，可以计算剪切区某一材料质点经过该区域的总时间ttot=h/vys。

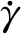
(17)

(18)

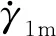
(19)

(20)

主剪切区的热源来自材料的塑性变形，剪切区瞬态温度分布可由热传导方程计算[23]。由于剪切区空间尺寸较小，故传热方程忽视了热扩散的影响。同时，在稳态切削过程中，温度随时间的偏导数为0。因此，热传导方程可以简化为只有热对流和热源项：

(21)

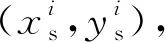
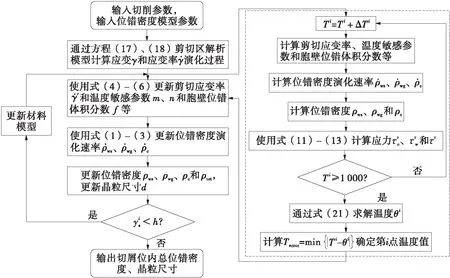
图4 剪切区微观组织演化的解析模型流程图

首先，认为主剪切面上的剪切应力分布是均匀的，剪切面的作用力为

(22)

切削力在切削方向和垂直方向的分量分别为

(23)

(24)

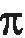
4 结果与分析

4.1 剪切区应变、应变率和温度的演化

理解应变、应变率和温度的联合演化,将有助于解释观测到的微观组织和确定有利的应变条件。根据图4所示的解析模型，使用速度分别为103.3和147.6 m/min的直角切削OFHC Cu的案例来分析晶粒细化模型的输入变量(应变、应变率和温度)随切削参数的变化规律。使用前角为0°的硬质合金刀具，切削深度为0.213 mm，切削宽度为4 mm，参数的组合来源于文献[8]。首先输入切削参数和刀具角度，计算出主剪切区的应变和应变率，根据主剪切区ys方向材料质点流动的特征，确定应变和应变率随着时间的变化过程。根据图4中结合位错密度模型的温度求解方法，计算温度在剪切区的分布。

切削速度分别为103.3和147.6 m/min时剪切区厚度方向上的应变、应变率和温度的演化过程如图5所示。可以看出，在剪切区的入口边界处和出口边界处的应变率均为0，应变率最大值在主剪切区AB上，从剪切区入口到剪切区出口边界，应变逐渐增大然后趋于稳定，温度也逐渐升高且与应变呈现出相同的趋势。假设切屑形成过程中切屑内某一点需要经过图5所示的变形和温升，则增大切削速度，会导致剪切区应变降低，应变率增大，切削温度升高；当切削速度增大时，材料流经剪切区的时间缩短，材料的变形过程更加对称。由于总应变是变形区各层局部应变的累积，在较低的切削速度下，工件材料受到更多的时间和空间范围内外力的作用，故切削速度降低会导致切屑内应变增大。

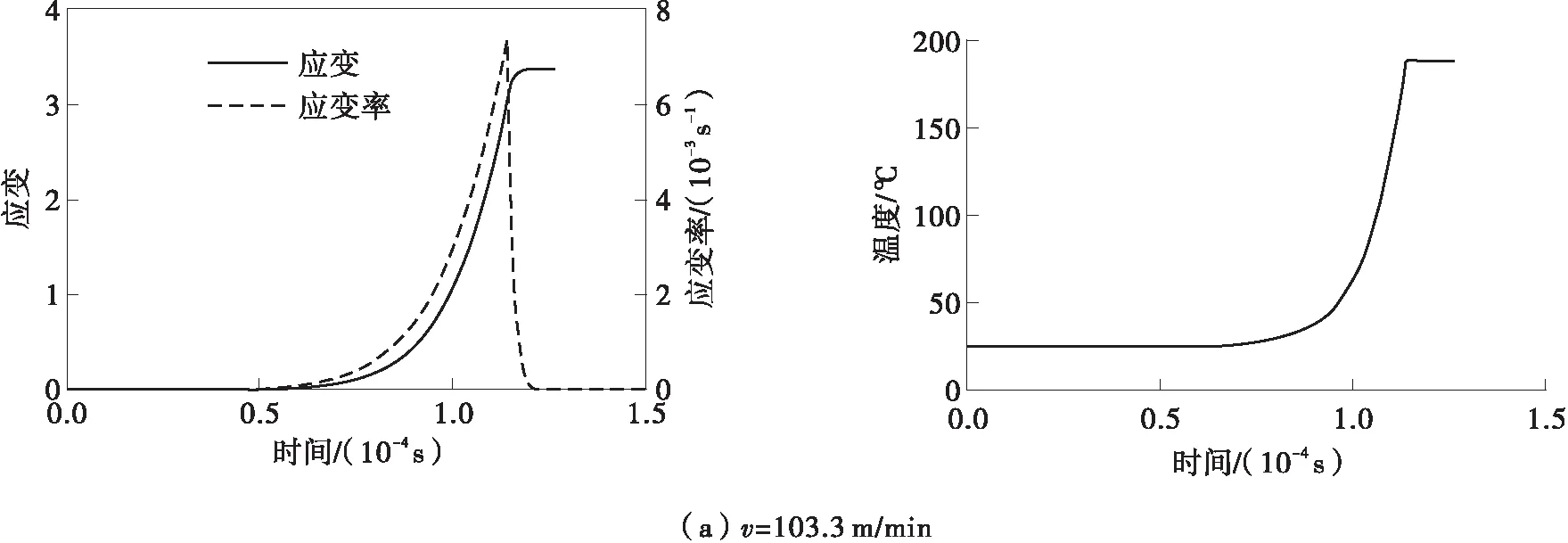
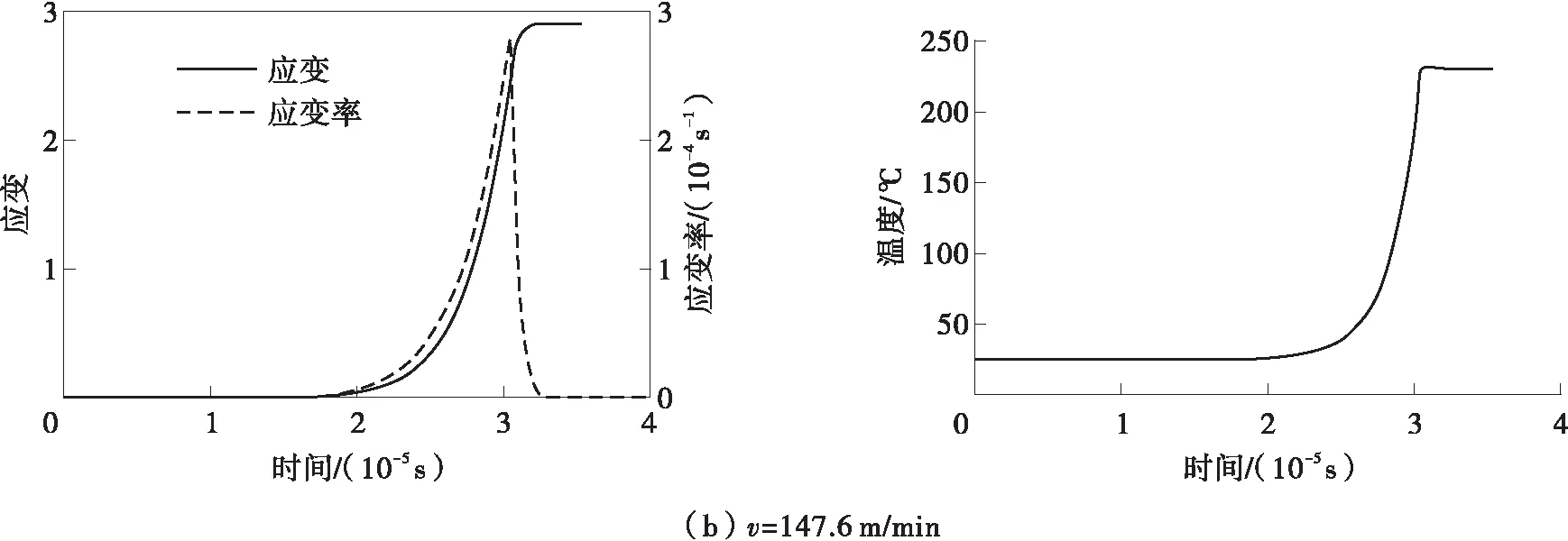
图5 剪切区的塑性应变、应变率和温度的演化

4.2 切削速度对切屑内微观组织的影响

采用本文模型分析了切削速度与显微组织(晶粒尺寸和位错密度)的关系，切削速度取为10.3、26.6、103.3、147.6和265.7 m/min，其余参数与4.1节分析所使用的参数相同，切屑的总位错密度与晶粒尺寸随着切削速度的变化如表1所示。从表中可知，切屑的总位错密度与晶粒尺寸随切削速度的增大表现出相反的变化关系。因为切削速度增大会导致变形区温度升高，应变降低，应变率增大，如4.1节分析的过程变量(应变、应变率和温度)与切削速度的关系所示。同时，增大切削速度会导致剪切角增大，主剪切区厚度减小，表明更少的材料颗粒参与塑性变形，因此所产生的变形能量减少，去除材料所需的切削能降低，位错能也降低，导致晶粒尺寸增大。Ding等[15]指出，在低应变、高切削速度和高切削温度条件下，切屑内的晶粒尺寸会增大。关于位错密度减小和晶粒尺寸增大的现象在Atmani等[5]的研究中也被发现。

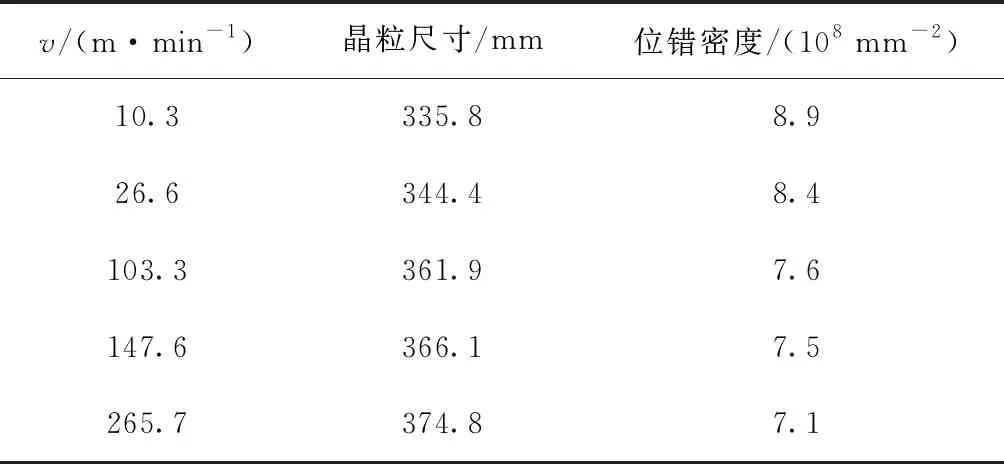
表1 OFHC Cu的切屑中位错密度和晶粒尺寸随切削速度的变化

4.3 预测结果及分析

4.3.1 剪切区力学行为预测分析

在切削过程中，刀具所受力的建模主要考虑切屑形成力，计算式见式(22)-(24)。图6给出了较大切削速度范围内切削力测量值Fx,exp和Fy,exp与本文模型的预测值Fx,USD-DD和Fy,USD-DD，切削参数与4.1节分析所使用的参数相同，图中同时给出了文献[8]材料模型的预测结果Fx,FEM和Fy,FEM。从图6(a)可以看出，切削力的预测趋势和大小与测量值吻合较好。UDS-DD解析模型与文献[8]模型均很好地预测了较大切削速度范围内切削力的变化，但UDS-DD模型在低速和高速情况下的预测值更接近于实验值。文献[21，23]分析指出，切削力随切削速度的增大表现出下降趋势，本文预测结果与文献[21，23]的分析结果一致。切削力下降的原因是由较高的变形速率和伴随的热软化效应导致的，如图5所示，当切削速度增大时，剪切区应变率增大，温度升高。根据前面的分析，在低的切削速度下，所产生的应变能较大，去除材料所需的切削能也较高，故在较低切削速度下会产生较高的切削力。

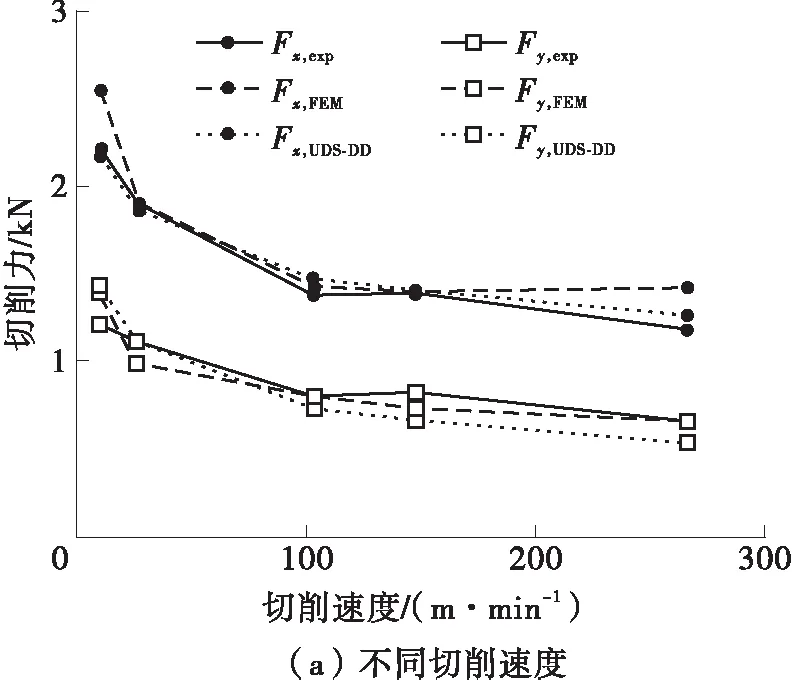
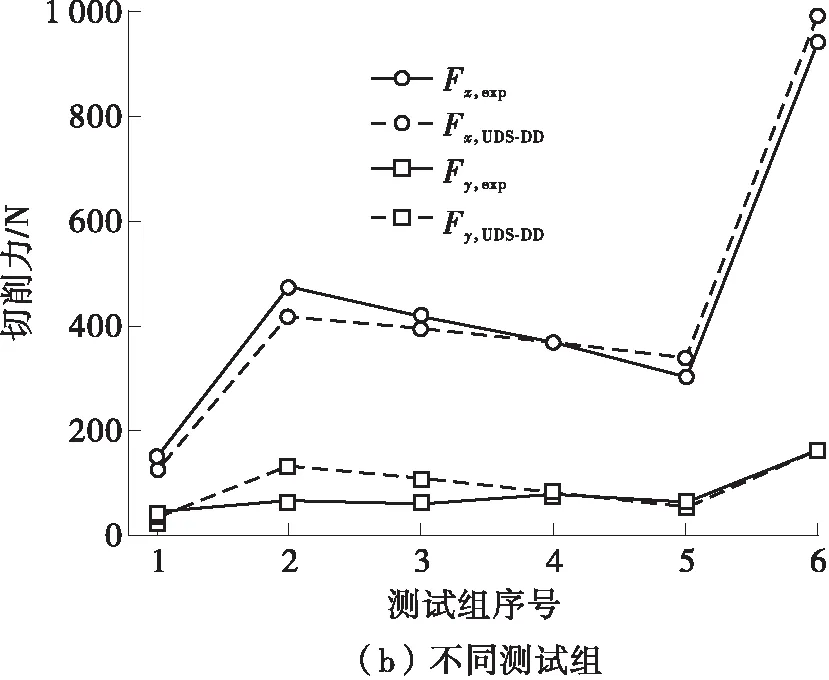
图6 OFHC Cu的切削力观测值和预测值对比

为了进一步验证本文模型预测直角切削OFHC Cu的切削力的可靠性，使用6组不同切削条件下硬质合金刀具直角切削OFHC Cu的切削力数据(见表2)[24]进行分析，其中切削宽度和前角分别为3.25 mm和+30°，本文模型对切削力的预测结果如图6(b)所示。测试组2-5的切削速度不断增大、其余切削条件不变，可以看出，UDS-DD模型预测的切削力与实验切削力的变化趋势一致，主切削力预测误差达到7.8%；测试组1、4和6的切削深度不断增大，可以观测到切削力也不断增大，且变化趋势更明显，这是因为切削深度的增大会直接影响到切削变形和刀具-切屑摩擦的增大[19]，从而引起切削力的增大。不同切削参数下OFHC Cu的切削力的有效预测间接证明了本文提出的剪切区微观组织演化模型的有效性，且与经典金属切削理论得到的力学行为相一致。

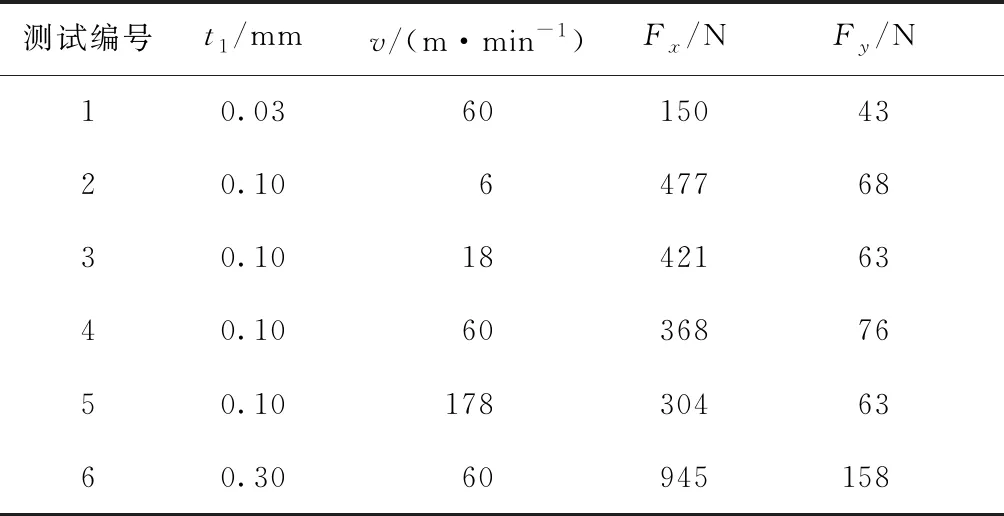
表2 不同切削条件下测量的切削力[24]

4.3.2 剪切区微观组织演化预测分析

Ding等[15]基于有限元方法在Ni等[25]的实验基础上对切屑内微观组织进行了预测，其结果和本文模型的预测结果如表3所示。从表中可知：无论是OFHC Cu还是Al 6061 T6，UDS-DD模型预测的切屑内晶粒尺寸与FEM的预测趋势非常接近，本文模型能反映切削厚度、切削速度和前角对剪切区晶粒细化的影响；在切削Al 6061 T6且前角减小时，根据式(15)可知，剪切角也会减小，因此剪切区塑性变形增大，导致位错演化速率增大，切屑内位错密度增大，晶粒细化加剧。

与Ni等[25]的实验观测结果相比，本文模型预测的切屑内晶粒尺寸误差为25%，而Ding等[15]结合FEM的预测误差为26%，本文方法与有限元方法的预测效果一致。本文模型没有考虑第二变形区对切屑形成过程中微观组织的影响，因为Atmani等[5]的研究结果显示，当金属材料经过剪切区后，第二变形区的摩擦和挤压对较宽切屑厚度范围内的微观组织的影响并不显著，在面积较大范围内切屑的位错密度和晶粒尺寸的演化主要发生在剪切区内。

表3 直角切削OFHC Cu和Al 6061 T6的预测结果

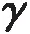
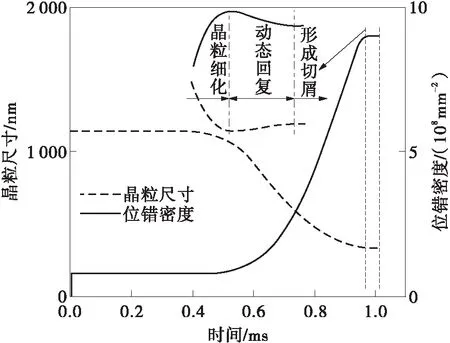
图7 切削OFHC Cu时剪切区位错密度和晶粒尺寸的演化过程

由于温度和应变的累积，此时切屑内发生动态回复，导致位错重新排列和湮灭，位错密度曲线出现轻微的隆起现象，导致晶粒尺寸出现小幅度的增大，同样的切屑动态回复现象在殷晓龙等[11]的常温切屑环境下也被发现了。式(1)和式(2)中的动态回复项表示：随温度的升高，该高温区域的位错积累率降低，从而引起晶粒尺寸的小幅度增大。该现象在文献[5，26]的模拟中也可以观测到。通过变形区后，细长的亚晶粒会断裂并形成等轴晶，切屑内位错密度和晶粒尺寸趋于平稳，因为切屑不再受到严重的塑性变形的影响，此时切屑内微观组织不再发生剧烈的变化，位错密度达到8.88×108mm-2，晶粒尺寸为331 nm。切削过程中晶粒细化过程的简化示意图如图8所示。

4.4 实验结果及分析

为了进一步验证模型的有效性，搭建了直角切削实验平台，使用型号为C6136HK的数控机床对Al 6061 T6棒材(φ200×80 mm)进行切槽加工，切削过程未使用切削液，得到槽深和槽宽约5 mm且切削宽度为3 mm的环形凸起表面，然后对外圆表面进行直角车削，同时采用KISTLER压电测力计9257B测量切削过程中的切削力。使用的Al 6061 T6材料性能参数和位错密度模型参数同4.3.2节。使用刃宽为5 mm的硬质合金MGMN500型切槽刀具，其刃口形貌及结构如图9所示，其中re为刃口半径；使用Alicona刀具形貌观测仪器测量了切槽刀具的刀尖钝圆半径、刀具后角和前角。

本文实验使用的刀具刃口半径约为35 μm，而文献[8，24]使用的刀尖刃口半径不足10 μm。当刀尖刃口较大时，为了更加精确地预测切削力，切削力的组成需要考虑犁耕力的影响[27]，本文使用滑移线场模型[28]来预测犁耕力，犁耕力计算公式见附录A。将3组不同的切削参数组合代入如图4 所示的预测模型，然后根据式(22)-(24)和式(25)-(30)分别计算切屑形成力和犁耕力，模型预测得到的切削力与实验观测的切削力如图10所示。从图中可知，切削力预测值与实验值具有较好的一致性，主切削力和垂直方向的力的预测平均绝对误差分别为6%和9%，证明了本文模型在预测切削力时的可靠性。

(a)刃口形貌

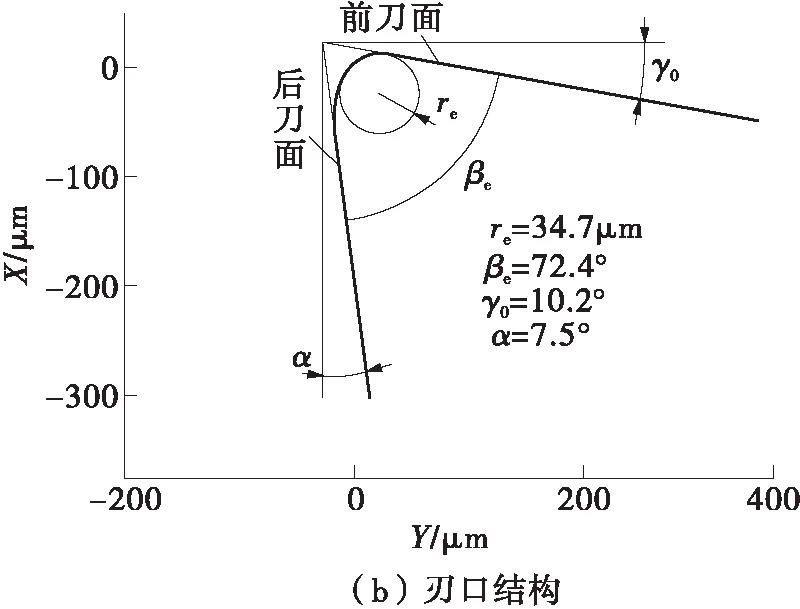
图9 切削刃的形貌和结构

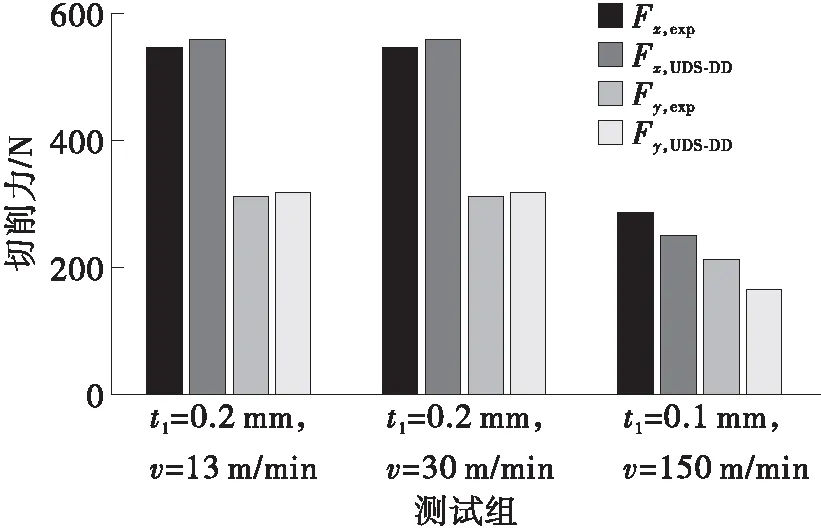
图10 直角切削Al 6061 T6切削力预测值

对切削参数为t1=0.2 mm和v=13 m/min的切屑进行离子减薄，然后使用透射电子显微镜(TEM)进行观测，得到如图11所示的切屑的TEM图像。使用Nano Measurer粒度分析软件对TEM内的晶粒尺寸进行观测分析，切屑中含亚微米级亚结构，切屑内晶粒基本上由拉长晶粒(长度<1 000 nm，宽度>100 nm)和等轴晶粒(直径200～700 nm)组成，有大量位错缠结形成位错积塞区，位错密度较高。

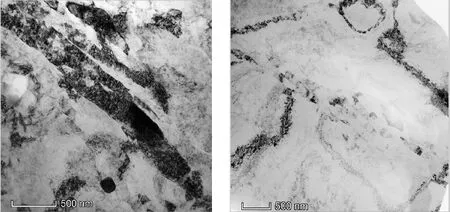
(a)拉长晶粒 (b)等轴晶粒

当直角切削Al 6061 T6的参数为t1=0.2 mm和v=13 m/min时，使用本文模型对切屑内位错密度和晶粒尺寸的演化过程进行建模，结果见图12。从图中可以看出，切屑内微观组织演化过程与图7中OFHC Cu切屑内的微观组织演化过程相似，均由剪切区严重塑性变形引起的位错运动导致。通过TEM观测到的切屑内平均晶粒尺寸约为591 nm，模型预测的切屑内晶粒尺寸为620 nm。结合4.3节中的预测结果，证明了非等距剪切区应变场、温度场和位错密度模型相结合，可以预测切屑内微观组织的演化过程。

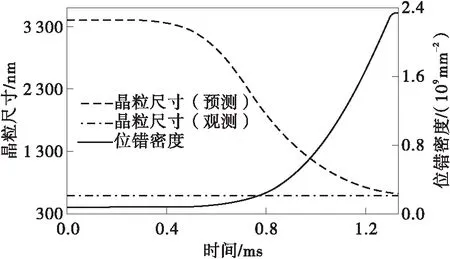
图12 切屑内位错密度和晶粒尺寸的演化过程

5 结论

本文提出了一种剪切区非等距分布和位错密度相结合的剪切区微观组织演化解析模型(UDS-DD)，通过对OFHC Cu和Al 6061 T6的直角切削模拟，在不同的切削参数范围内对切削力和晶粒尺寸进行了预测。切削模拟结果表明：切削速度增大会导致切削力降低，增大切削厚度会导致切削力增大，该趋势与经典切削力学理论相一致。切屑内晶粒尺寸的预测结果与实验数据具有很好的一致性，UDS-DD模型较好地反映了稳态切削过程中切屑的微观组织演化过程的基本特征。