一种基于QAP问题的ZK-SNARK新协议

黄平 梁伟洁

(华南理工大学 数学学院，广东 广州510640)

人们在享受着日益高效便捷的信息化服务的同时，信息安全与隐私保护问题也越发突出和尖锐，逐渐成为制约社会发展的瓶颈和挑战。密码学是构建和保障现代信息安全的强有力工具，在众多的现代密码学技术中，零知识证明(ZKP)理论因其证明可靠、泄密零化的鲜明特质符合人们对网络世界中信息的真实性和隐秘性需求而备受关注。ZKP由Goldwasser等[1]于1986年提出，它既是一种密码学思想，也是一项应用性很强的密码技术，旨在仅向验证方证明想要证明的结论外，证明方不因证明过程而泄露任何知识。零知识证明协议就是实现这一思想的证明系统。Goldwasser等构造的零知识证明协议是交互式的，随后Blum等[2]于1988年引入随机的公共参考串模型(CRS)，首次构造出非交互式零知识证明(NIZKP)。非交互式零知识证明是单向的，较交互式零知识证明具有更高的便利性和适用性。目前在非交互式零知识证明中，ZK-SNARK协议最为成熟。通过应用ZK-SNARK协议，Ben-Sasson等[3]设计出隐私性极高的零钞(Zcash)区块链数字货币系统。

Gennaro等[4]于2012年提出了二次算术程序(QAP)形式的非确定性多项式(NP)问题，并基于强QAP问题构造了ZK-SNARK。ZK-SNARK的优越性在于：计算复杂度是拟线性的[5- 7]，这使其是计算可行的；产生的证据量关于问题的规模是常数阶的。人们将Gennaro等构造的ZK-SNARK协议称为GGPR协议。GGPR协议是基于强QAP构造的，对于一般的QAP，需要先将QAP转化为强QAP，再运行ZK-SNARK。然而，一般的QAP转化为强QAP后，QAP问题的度扩大3倍以上，严重影响了运行效率。Parno等[8]对此进行了改进，提出了PGHR协议(该协议弱化了QAP问题)，基于一般的QAP构造ZK-SNARK系统，并将证据量由原来的9个群元素降低为8个，极大提高了ZK-SNARK的工作效率。不过，PGHR协议相比GGPR协议增加了密码安全性假设。

在生成CRS时，PGHR协议为QAP的多项式引入了额外的常系数因子，以增加随机性。PGHR协议设计验证式的思想是单一化的，即一个验证式实现一个条件的验证，忽略了验证式的联合效应。本文在PGHR协议的基础上，通过利用额外系数因子的互不整除性与验证式的联合效应将PGHR协议进一步压缩，得到新的ZK-SNARK协议，称为CPGHR协议，给出了新协议安全性的严格证明，并对协议的有效性进行理论分析与实验验证。

1 预备知识

首先，引入文献[9]中一些符号表示法。设函数f,g:N→[0,1]，若 ∀c>0，|>f(k)-g(k)|=O(k-c)，则记f(k)≈g(k)。若f(k)≈0，则称f关于k是可忽略的，记作negl(k)。poly(x)表示x的多项式。y=A(x;r)表示算法A输入x和随机因子r后输出y。y←A(x)表示随机选取r，并令y=A(x;r)。(y;z)←(A‖B)(x)表示y←A(x),z←B(x)。若S是一个概率空间，则y←S表示根据S的概率分布，从S随机选取y；若S是一个有限集合，则y←S表示从集合S中均匀随机抽取y。Pr[A]表示事件A发生的概率，Pr[A|>B]表示条件概率，Pr[x←S;y←T;…:p(x,y,…)]表示依次执行x←S,y←T等后，关系p(x,y,…)为真的概率。1κ表示κ个1的级联。若x是一个二进制串，则|>x|表示x的长度；若x是一个整数，则|>x|表示x的二进制串的长度，称为x的长度。[m]表示集合{0,1,…,m}。

1.1 一些重要概念

定义1Π=(G,P,V)是由NP关系R定义的语言L的一个SNARG系统，若满足下列性质：

(1)可行性，即∀(u,w)∈R，

(2)可靠性，即对任意非一致概率多项式时间敌手A，

(3)简洁性，即证据的大小

一般来说priv≠crs，此时上述SNARG称为指定验证方的。特别地，当priv=crs时，由于验证方无需特定的秘密信息，所有的验证者均可验证，因而此时的SNARG称为公开可验证的。

文献[4,11]在SNARG基础上定义了SNARK和ZK-SNARK。

上述零知识的定义是统计零知识的。零知识性保证了证据除了揭示证明方知道陈述u的解外，不泄露任何其他知识。由NIZK的定义[2]可知，ZK-SNARK是一个NIZK系统。

上述定义的关系结构如图1所示。

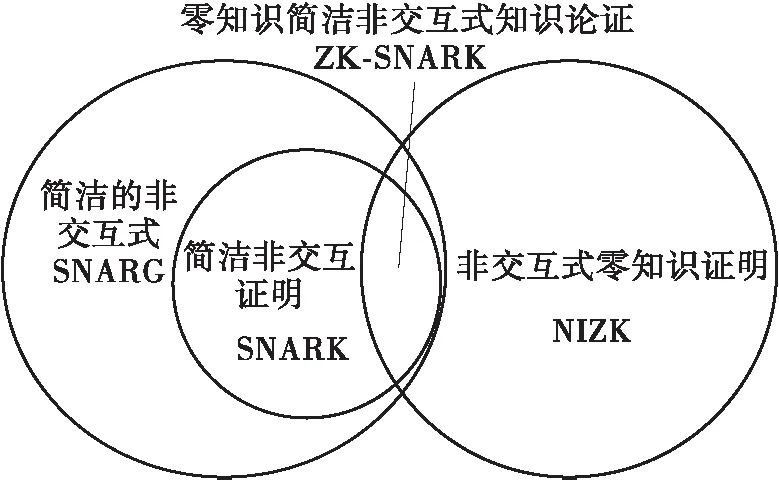
图1 一些定义的关系

1.2 椭圆曲线群与双线性对

有限群和双线性对是ZK-SNARK实现加密的关键技术。由于本文提出的新协议是基于椭圆曲线密码体制描述的，因此这里给出与之相关的定义和性质。

定义4 域F上的椭圆曲线E由下述方程定义[12]：

E:y2+a1xy+a3y=x3+a2x2+a4x+a6,

其中a1,a2,a3,a4,a6∈F且Δ≠0，Δ是E的判别式。若L是F的扩域，则E上的L有理点集合是E(L)={(x,y)∈L×L:y2+a1xy+a3y-x3-a2x2-a4x-a6=0}∪{}，其中是无穷远点。

定义5 点集E(L)配备“弦和切线”加法运算[12]构成一个加法交换群，称为椭圆曲线群，其中无穷远点是单位元。

定义6设G1和G2是两个加法群，GT是乘法群，P∈G1,Q∈G2,g∈GT，如果存在有效映射[13- 14]e:G1×G2→GT，即e(P,Q)=g，对任意P1,P2∈G1和Q1,Q2∈G2，满足：

e(P1+P2,Q1)=e(P1,Q1)e(P2,Q1)，

e(P1,Q1+Q2)=e(P1,Q1)e(P1,Q2)，

那么映射e称为从G1×G2到GT的一个双线性对。

双线性对满足如下基本特性[13- 14]：

(1)双线性性，即对任意P∈G1,Q∈G2,n∈Z，有e(nP,Q)=e(P,Q)n=e(P,nQ);

(2)非退化性，即一定存在P∈G1,Q∈G2使得e(P,Q)≠1GT，其中1GT是GT的单位元；

(3)可计算性，即存在有效的多项式时间算法计算出双线性对的值。

1.3 算术电路与QAP问题

许多NP问题可以表示为多项式函数的形式，例如求给定一个单向函数的象的原象。而一个多项式函数可以转化为一个算术电路，Gennaro等[4]定义了QAP并证明了算术电路可以转化为QAP。就像算术电路一样，QAP也存在可满足性问题[6，15]，简称QAP问题。基于QAP问题可以构造ZK-SNARK，这就是Gennaro等验证一个NP关系的零知识证明方案。下面给出QAP的定义及相关性质。

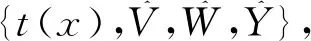
设关系R={(u,w)∈Fn′×Fn:φ(w)=u}，其中u∈Fn′是陈述，w∈Fn是对应的解，则关系R定义了一个可满足性问题，给定具体的u便得到了一个问题实例。由于函数φ与QAPQ具有对应关系，那么QAPQ也自然产生一个可满足性问题。

以下引理保证了算术电路可以转化为QAP，证明详见文献[4]。

引理1 假设C是域F上输入来自Fn、含s个乘法门的算术电路，那么存在规模为n+s、度为d的QAP计算C。

2 新协议的构造

由于本文的研究主要针对协议层，而非从算术电路到QAP转化的改进，也非ZK-SNARK协议的具体实现算法的优化，在不影响实质的条件下避繁就简，以下直接从QAP问题出发给出ZK-SNARK新协议CPGHR。

图2 新协议系统ΠLQ的结构

2.1 新协议的描述

在运行系统之前，首先选定系统公共参数：生成元分别为P1、P2的r阶加法群G1及G2和r阶乘法群GT，双线性映射e:G1×G2→GT，定义同态映射E1(x)=xP1,E2(x)=xP2,x∈Z。域F=Iq，q是素数。令指标集Imid={1,2,…,m-n′}，Iin={m-n′+1,m-n′+2,…,m}。

(1)(PKQ,VKQ)←Gen(Q)

输入QAPQ，CRS生成器Gen在F*上随机选取s、α、β、γ，在[q/4,q]中随机选取rv，在(rv,2rv)中随机选取rw，由此得到的rv、rw互不整除，并令ry=rvrw，输出证明方CRS

PKQ=({E1(rvvk(s))}k∈Imid,

{E1(αrvvk(s))}k∈Imid,{E2(rwwk(s))}k∈[m],

{E1(yk(s))}k∈[m],{E2(si)}i∈[d],

{E1(βrvvk(s)+βrwwk(s)+βyk(s))}k∈[m])

及验证方CRS

VKQ=(E1(rvv0(s)),{E1(rvvk(s))}k∈Iin,

E2(γ),E2(αγ),E1(βγ),E2(βγ),E2(ry),

E1(ryt(s)))。

第二个模块验证如下3个等式：

若这些等式均成立，则Verify输出1，否则输出0。

2.2 新协议的零知识化

为得到ZK-SNARK协议，需要对SNARK协议零知识化。按照GGPR协议的方式将上述CPGHR协议零知识化是容易的。证明方从F中随机选取δv、δw、δy，并令V′(x)=V(x)+δvt(x),W′(x)=W(x)+δwt(x),Y′(x)=Y(x)+δyt(x),h′(x)=h(x)+δwV(x)+δvW(x)+δvδwt(x)-δy。不难发现，V′(x)W′(x)-Y′(x)=h′(x)t(x)，因此，证明方只需基于V′(x)、W′(x)、Y′(x)、h′(x)生成证据即可。由于V′(x)、W′(x)、Y′(x)中包含了t(x)，证明方CRS PKQ及证明方计算需要相应调整，验证方及其CRS VKQ保持不变。由此随机化后得到的方案具备统计上零知识性，证明见文献[4]。

2.3 新协议的直观解释

3 安全性证明与性能分析

3.1 安全性证明

由定义可知，上述协议系统ΠLQ=(Gen,Prove,Verify)的可行性和简洁性是自然的。接下来需要证明该系统的可靠性，具体表述为如下定理。

定理1如果q-PDH假设和d-GKCA假设成立，其中q≥max{2d-1,d+1}，那么在定义2下证明系统ΠLQ是可靠的SNARK，且纳伪率φ≤(q/4r)-1。

在给出定理1的证明之前，先引入相关的密码安全性假设和证明需要用到的引理。

3.1.1 密码安全性假设

设κ是安全参数，q=poly(κ)，A是非一致概率多项式时间敌手。

假设1(q-PDH)q次Diffie-Hellman假设[9]成立，若对任意敌手A，有

Pr[(r,G,GT,e)←G(1κ);P←G(〗1};s←F*;

y←A(r，G，GT,e,E(1),E(s),…,E(sq),

E(sq+2),E(sq+3),…，E(s2q))：

y=E(sq+1)]=negl(κ),

其中E(x)=xP。

假设2(q-KCA) 系数安全性假设成立，若对任意敌手A，存在非一致概率多项式时间提取器χA，满足

Pr[(r,G,GT,e)←G(1κ);P←G(〗1};α,s←F*;

σ=(r,G,GT,e,E(1),E(s),…，E(sq),

本文将q-KCA假设强化，提出q-GKCA假设，因为q-KCA假设成立可以推导出q-GKCA假设成立，所以q-GKCA的安全性不低于q-KCA假设。

假设3(q-GKCA) 系数安全性假设成立，若对任意敌手A，存在非一致概率多项式时间提取器χA，满足：

Pr[(r,G1,G2,GT,e)←G(1k);P1←G1{1},

P2←G{1};α，s←F*;σ=(r,G1,G2,GT,

e,E1(m0),E1(m1),…，E1(mk),E2(αm0),

E2(αm1),…，E2(αmk)),k∈N,

n∈[k]]=negl(κ),

其中E1(x)=xP1,E2(x)=xP2。

引理1F[x]上全体至多k次多项式记为F[x](k)，F[x]上xk的系数为0的全体多项式记为F[x]。给定d，设U={uk(x)}⊂F[x](d)，由U中的多项式的线性组合生成的多项式集记为span(U)，那么存在a(x)∈F，使得{a(x)uk(x):uk(x)∈U}⊂F[x]。

引理1的证明见文献[4]。

3.1.2 定理1的证明

(1)V(x)W(x)-Y(x)=h(x)t(x)；

且(θ0,θm-n′+1,θm-n′+2,…,θm)=(1,am-n′+1,am-n′+2,…,am)。

首先证明结论①成立。

注意到，验证方的验证式(2)为

b2,jrwwj(s))。下面证明，此时验证方以不超过(q/4r)-1的概率验证通过(3)式：

由于rv、rw互不整除，ry=rvrw，(3)式成立必须满足以下两个条件：

a)rv整除b2,jwj(s)；

接下来证明结论②成立。

对于同态映射E1≠E2的一般情形，敌手A能构造虚假证据，那么在E1=E2=E的特殊情形下，更是如此。给定q-PDH问题σ=(r,G,GT,e,E(1),E(s),…,E(sq),E(sq+2),E(sq+3),…,E(s2q))。因为q>d，故随机选取互不整除的rv、rw，并令ry=rvrw后，则B可以通过σ生成{E(si)}i∈[d],

{E(rvvk(s))}k∈[m],{E(rwwk(s))}k∈[m],

{E(yk(s))}k∈[m],E(ry),E(ryt(s))。

令P={rvvk(x)+rwwk(x)+yk(x)}∪{xd}，由引理1，随机选取a(x)∈F[x](d+1)，使

{xq-da(x)p(x):p(x)∈P}⊂F[x]。

令β=sq-da(s)，则B可通过σ生成E(βp(s)),∀p(x)∈P，这是因为βp(s)=sq-da(s)p(s)的次数至多为q-d+d+1+d=q+d+1≤2q，且sq+1的系数为0。因此，B可以生成

{E(βrvvk(s)+βrwwk(s)+βyk(s)):k∈[m]}。

同理，随机选取γ′∈F*，令γ=γ′sd，那么B可以生成E(γ)和E(βγ)。以同样的方式，B生成{E(αrvvk(s)):k∈Imid}和E(αγ)。由此可知，B在没有求解q-PDH的情况下可以为A生成有效的CRS。

综上，在定义2下，由q-PDH和d-GKCA假设(q≥max{2d-1,d+1})可知，上述证明系统是可靠的SNARK，且纳伪率φ≤(q/4r)-1。证毕。

3.2 性能分析

3.2.1 理论分析

为评估新协议的改进效率，下面将新协议与PGHR协议的算法复杂度进行对比分析。由于ZK-SNARK协议的实现开销主要在于群和双线性对运算，这里仅考虑ZK-SNARK协议实现过程中涉及到的群和双线性对运算的复杂度。为方便起见，这里将椭圆曲线群和双线性对计算一般化。约定椭圆曲线群加法运算用字母J表示，点乘运算用字母M表示，双线性对运算用字母H表示。

表1 CPGHR协议与PGHR协议的算法复杂度对比

由表1可以看出，相对于PGHR协议，CPGHR协议更加精简高效。首先，CRS和证据量得到了缩减：在m远大于n′和d的场合，CRS大致压缩为原来的71%；证据量由8个群元素降低为6个，压缩率为75%。其次，CRS与证据量的压缩带来系统整体运算效率的提升是自然的，新协议对于CRS生成、证明方与验证方计算都有不小的提升。假定椭圆曲线运算开销是均匀的，那么理论上，在m远大于n′和d的场合，CRS的生成效率及证明方执行椭圆曲线群运算的计算效率大约提高28%。在n′很小的场合，仅考虑双线性对运算时，验证方的计算效率大约提高33%。

3.2.2 实验分析

本文以图3所示的算术电路为实例，取算术电路输入c1=c2=100,c3=1 000，对CPGHR协议和PGHR协议进行模拟测试。

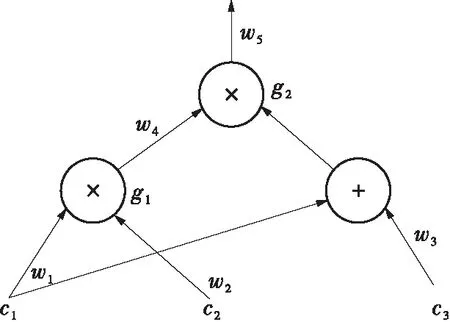
图3 一个算术电路实例

采用C++语言编程，使用PBC库中的A类双线性对实现椭圆曲线群和双线性对底层运算，群的阶数r选为160位素数，基域阶选为512位素数，100次实验结果见图4。首先，数据的波动性主要来源于协议底层的椭圆曲线与双线性对运算。从图中可以看出，PGHR协议与CPGHR协议的运行效率数据的线形是一致的，反映为效率提升值曲线的平稳性，这在一定程度上说明实验是平行化的。因此，对各实验结果取均值是合理的。为了将实验结果与理论分析结果更好地进行对比，本文将各实验结果取均值汇总，结果如表2所示，其中不考虑CRS的稀疏存储及多项式除法的时间开销。

(a)CRS生成效率

(b)证明方计算效率

(c)验证方计算效率

表2 平均性能对比

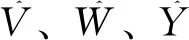
4 结论

在运用验证式联合效应的思想指导下，本文在PGHR协议的基础上做了改进，提出了更加精简高效的ZK-SNARK新协议，并对新协议的安全性、有效性进行证明和分析。新协议相较于PGHR协议的改进在于：

(1)降低了密码安全性假设要求，使其回到与GGPR协议相同的水平。

(2)进一步压缩CRS大小和证据量，CRS的大小从7m-n′+d+10个群元素降为5m-n′+d+10，其中m、n′、d是问题的规模参数，理论最小压缩率约达71%；证据量由8个群元素降为6个，压缩率达75%。

(3)提高了CRS生成计算、证明方计算效率，理论最大提高值达28%。

(4)减少了验证方双线性对的运算次数，使其从原来的12次降为8次，验证方计算效率提高了约33%。

新协议相对于PGHR协议在空间和时间开销方面均得到有效优化，这对于ZK-SNARK协议的应用具有积极的意义。特别指出，在实际应用中，证据往往需要通过网络进行传输，特别是在区块链的应用场景中，证据需要高频传输，并写入区块链系统中，证据量的压缩更加节省存储空间，也在一定程度上提高了传输效率，而证明方计算效率的提高进一步缩短了生成证据的时间，这对于需要进行高频交易的小容量区块链系统而言意义重大。

此外，本文的改进工作是协议层的，这意味着针对PGHR协议的具体实现算法的优化同样适用于新协议。