绿色发展理念下中国能源消费与碳排放的预测分析

郝园园

摘 要：自1990年以来，世界各国开始重视全球气候及能源在经济发展中的作用、追求低碳经济发展以及有效利用能源和减少环境污染的模式。改革开放加快了中国工业化生产和城市化发展进程，致使能源总消耗的需求量急剧增加，并且能源消耗产生的碳排放量不断增加。“十三五”规划提出了绿色发展理念，绿色经济是在经济高速发展过程中实现能源的低消耗、能源效率的高转化以及与环境和谐共处的发展模式。所以在保持经济高速增长的同时，励志于改变国民生产和生活方式，提高绿色低碳水平，有效控制碳排放总量，也是中国未来发展过程中一项具有约束力的目标。低碳经济是必要性、可行性的，是实现经济长久健康发展的必要途径，也是推动社会文明建设的必然选择。为了预测中国经济发展中的能源消耗和碳排放，GM（1，1）预测模型主要用于预测能源消耗和碳排放的未来发展趋势，对于改善能源消耗和碳排放具有一定的参考意义。

关键词：能源消费;碳排放;GM（1，1）预测模型;能源资源;煤炭资源

中图分类号：F206 文献标识码：A 文章编号：2096-0298（2021）01（b）--03

能源资源是社会经济发展的动力中枢，是国民生活、生产与发展的物质基础保障。回顾历史，能源的发展离不开社会的进步与发展，反之经济发展是以能源资源为核心，能源也是以经济发展为基础保障。自20世纪80年代以来，我国的经济不断加速发展，能源消费量也随之增加。目前我国的一次能源结构主要以煤炭为主，虽然近年来风电、光伏、核能等可再生能源快速发展，对天然气的利用也有所增加，但从能源消费情况和能源消费结构上看，煤炭资源消费仍占据主导地位。在能源消费结构中，煤炭消费总量占一次能源消费总量的比例一直居高不下，平均比重占70%;其他能源仅占能源总消费的30%。以2018年为例，2018年煤炭能源消费总量约27.38亿吨标准煤，占能源总消费约59%，同比增长0.96%。随着我国石油、天然气、水电核产业的不断发展，对传统资源的消费有所减缓。天然气消费总量约3.62亿吨标准煤，占能源消费总量的6.77%，同比增长15.15%。石油消费量8.77亿吨标准煤，占能源总消费的3.9%，同比增长3.89%。风电核能源消费约6.64亿吨标准煤，占消费总量的14.3%，同比增长7.08%。由此可见，煤炭能源在我国能源消费结构中占有绝对主导地位，这也是导致温室气体（二氧化碳）持续增加的一个主要原因。然而在其他能源中，尤其是风、电、水和核能等绿色清洁能源的二氧化碳排放幾乎为零，但在我国的一次能源消费结构中占比不到10%。由此看来，在未来研究工作中，优化能源产业结构，能源消费方式的多元化以及提高能源效率将成为我国减少二氧化碳排放与实现绿色可持续发展道路的主导方向。此外，近年来我国风、电、水和核能等绿色清洁能源的比重呈缓慢增长的趋势。截至2018年，绿色清洁能源由1975年的4.6%增长到了14.3%。可见，我国已经意识到能源结构与消费方式的不合理问题，开始逐步优化能源相关产业结构代替传统产业，进一步实现低碳、绿色可持续发展的战略方针，同时也为进一步实现环境与社会经济发展共存模式奠定基础，实现能源消费多元化。党的十九大以来，我国一直提倡能源产业低碳、绿色、健康、可持续发展的战略，坚持能源节能减排、低碳绿色发展与环境共存和谐发展方针。同时努力实现能源产业结构升级和优化能源产业结构，降低能耗与提高能源的使用效率，未来在能源绿色可持续发展的道路上将面临严峻的挑战，其对于众多学者而言这也成为更具有意义的研究性课题。本文通过建立灰色GM（1，1）预测模型基于1975—2018年国家统计局数据，对我国能源消费和碳排放为指标变量进行分析预测。

1 灰色GM（1，1）预测模型理论

灰色预测主要是通过系统模型对确定性信息和不确定性信息进行系统性预测，也就是数据变量在一定周期内变动状况与时间相关的灰色过程以及针对数据变动轨迹和趋势的相似度进行分析预测。所以灰色预测GM（1，1）模型如下：

GM（1，1）预测模型的精度主要是通过模型的相对误差P和均方差比值C进行检验。如果预测值与原数列精度越高，表明模型的拟合度就越好，如表1所示。

2 非线性GM（1，1）预测模型理论

在经济发展过程中，能源消费和碳排放之间是否存在线性与非线性的关系，对其影响因素较为复杂。非线性GM（1，1）模型预测是基于灰色系统预测的数据处理后再次预测，是对数据误差修正的判断，对数据的预测具备可控性。通过GM（1，1）模型不断得出新的预测值、新的残差序列值，计算出一个新的参数，建立新的动态关系。所以预测数据与原始数据变化基本一致，具有良好的精准程度。非线性GM（1，1）模型是以经典GM（1，1）模型为基础，基于原始数据x（0）（k）与x（0）（k）的线性关系的假设。若x（0）（k）与x（1）（k）不满足线性关系的条件，那么非线性GM（1，1）模型对数据拟合度的预测更佳。即建立非线性GM（1，1）模型如下：

3 回归预测模型

回归预测分析主要是通过最小二乘法利用历史数据之间的因果关系建立回归模型进行预测。该方法适用于变量单一、影响因素简单化，并且预测精度高、使用方便、对数据可进行长期预测等特点。回归分析预测法包括一元线性回归预测法、多元线性回归预测法和非线性回归预测法等。在实际数据分析中，影响预测变量的因素存在多个，那么就要通过多元进行回归分析。在多元回归分析中大多数非线性回归都可转化为线性回归来实现，其多元线性回归分析的原理与一元线性回归分析原理完全相同。

4 GM（1，1）模型预测检验

4.1 能源消费GM（1，1）预测模型

在GM（1， 1）预测模型中，如果能源消费这一变量在一定周期内的变化趋势与时间相关，所以能源消费GM（1， 1）模型如下：

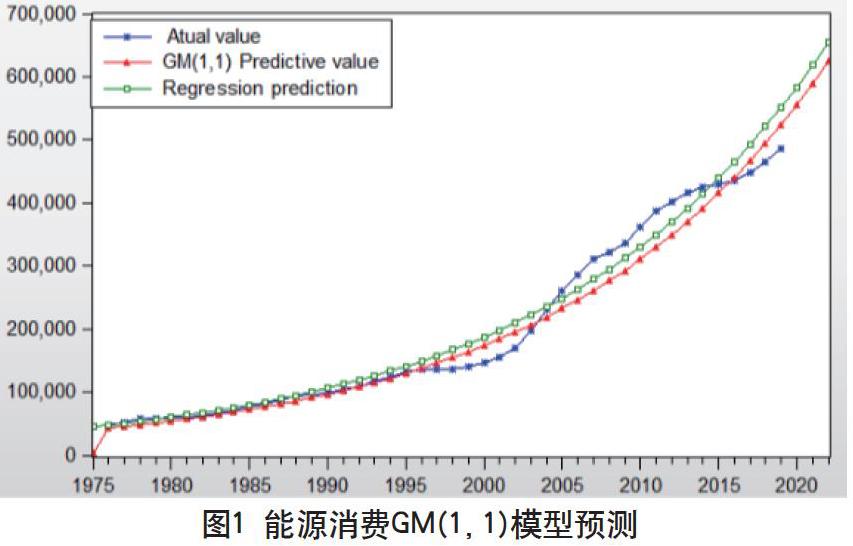
根据式（13）计算可知，能源消费GM（1，1）模型的精准度为P= 92.28% > 90%，所以GM（1，1）模型合格。由图1可知，利用GM（1，1）模型与回归预测模型的能源消费量预测值的走势和真实值的走势基本一致。GM（1，1）模型与回归预测模型相比，GM（1，1）模型更加准确存在误差较小。虽然预测结果都存在一定的误差，但对能源产业发展趋势具有一定的参考意义。2018年我国能源总消费464000万吨标准煤，随着我国的经济不断发展，未来我国能源总消费量将持续增长。如果中国的能源总消费和需求因素在未来四年内不发生重大变化，到2022年中国的能源消费总量将有可能增长至587415万吨标准煤，预计比2018年可能增长26.6%左右。

4.2 碳排放GM（1，1）预测模型

本節基于中国国家统计年鉴1975—2018年的碳排放数据，建立单一灰色GM（1，1）预测模型利用线性回归与统计方法相结合对能源消费进行预测。则碳排放GM（1，1）模型的时间响应序列如下：

根据式（13）计算可知，碳排放GM（1，1）模型的精准度为P= 88.5% > 80%，所以GM（1，1）模型合格。所以由图2可知，利用GM（1，1）模型与回归预测模型的碳排放量预测值的走势和真实值的走势基本一致。结合GM（1，1）预测模型和回归预测模型预测结果可知，随着经济不断的发展，二氧化碳的排放量不断增加，后期也存在上升的趋势，对环境与经济的协调发展带来巨大的考验。2018年我国碳排放总量超过101.45亿吨，在未来随着工业化经济不断发展，我国碳排放总量将有可能持续增长，如果中国的能源消费、人口等影响因素在未来四年内不发生重大变化，到2022年中国的能源消费总量将有可能增长至121.33亿吨左右，预计比2018年可能会增长19.5%左右。

通过灰色GM（1， 1）预测模型与回归预测模型对历史数据的预测分析，两种预测方法对我国能源消费量和碳排放的预测结果是有差距的，用回归预测模型所得的预测值大于GM（1，1）预测模型，更接近实际值。GM（1，1）预测模型对能源消费和碳排放的影响程度较大的因素充分考虑在模型中，通过已知变量来预测未来的趋势更具有解释性和理解性。

5 结语

本文基于经济发展数据对中国的能源消费总量以及碳排放总量进行了预测。对于中国能源消费总量和碳排放总量的预测，首先使用了灰色GM（1，1）模型，其次将对能源消费总量和碳排放总量具有重要影响因素考虑在内建立了回归预测模型，最后建立了中国能源消费的回归模型，预测了基准情景和低碳情景下中国2020—2022年的能源消费量以及碳排放量。因此，对于我国政府而言，在产业结构升级和宏观调控中起着至关重要的作用。第一，应加强政府对相关产业的干预与指导，制定绿色低碳可持续发展相关的政策体系，例如通过减税、风险补偿和专项资金等优惠政策鼓励中小企业进行产业结构优化与升级;第二，以完善健全碳排放交易市场和温室气体（二氧化碳）排放标准体系为目标，实行严格考核与问责制，促进绿色低碳技术推广与投入;第三，要建立健全的处罚制度，对工业企业进行定期监督检查，规范节能减排标准制度与执行力度，大力发展绿色节能环保产业，促进社会经济与环境的绿色协调可持续发展。

参考文献

谢凯，南灵.基于STIRPAT模型的陕西省建设用地对能源消费碳排放的影响[J].湖北农业科学，2016（03）：599-602.

荣蓉.山东省工业碳排放情景预测及减排策略研究[J].中外能源，2016（02）：94-100.

赵选民，段晓琛.基于STIRPAT模型的陕西省碳排放影响因素分析[J].财会月刊，2016（12）：31-34.

嫣嫣，李爽，夏青.中国居民生活用能碳排放影响因素分析——基于STIRPAT模型[J].生态经济，2017（05）：42-47.

武红，谷树忠，周洪.河北省能源消费、碳排放与经济增长的关系[J].资源科学.2011，33（10）：1897-1905.

冯思静，邓元月，马云东，等.中国能源消费预测灰色建模法[J].数学的实践与认识，2012，42（03）：78-84.

巧张勇，刘婵，姚亚平.GM（1，N）与GM（0，N）模型在能源消费碳排放预测中的比较研究[J].数学的实践与认识，2014，44（05）：72-79.

赖红松.基于灰色预测和神经网络的人口预测[J].经济地理，2004，24（02）：197-201.