海洋软黏土大直径沉桩贯入挤土效应

周 密，韩雨薇，周小文，肖自卫

（1.华南理工大学亚热带建筑科学国家重点实验室，广东 广州 510640；2.华南理工大学华南岩土研究院，广东 广州 510640；3.中铁南方投资集团有限公司，广东 深圳 518000）

随着海洋资源开发的不断扩张[1]，各类桩基础在我国港口和近海结构等工程中得到广泛应用。多桩体系是海洋工程中常见的桩基系统，而圆桩在贯入饱和海洋软黏土时，桩身将置换相同体积的土，产生巨大的侧向挤压应力，发生挤土效应，主要表现为沉桩时桩周土体发生水平位移和竖向隆起；桩周土体被重塑和扰动，应力状态发生改变，产生很高的孔隙水压力；土的原始结构遭到破坏，土体的工程性质与沉桩前相比发生了很大改变[2]。海洋桩挤土效应可能影响起重船的锚泊系统、导管架多桩基础施工等，严重时会因过大的水平位移而导致桩基础倾斜，造成工程事故。因此，研究圆桩贯入过程中桩周土体的变化规律对海洋桩基础桩体施工具有重要意义。

研究沉桩过程中挤土效应主要有圆孔扩张理论（CEM）、应变路径法（SPM）和有限单元法（FEM）[3]等三种常用方法。其中关于沉桩机理、孔隙水压力的产生与消散、单桩的极限承载力理论研究较多。王幼青等[4]为了分析挤土桩施工对相邻建筑设施的影响，在试验研究的基础上，采用Vesic圆孔扩张理论和Duncan-Chang 模型模拟土的力学性能。近年来，刘裕华等[5]应用假定有初始孔径的圆柱形扩孔理论对预制管桩施工引起的挤土效应进行了现场试验研究；周火垚等[6]在饱和软黏土中进行了足尺静压管桩挤土效应试验研究；江强等[7]基于实际工程开展了现场试验。而由于沉桩问题的复杂性，利用理论公式求得解析解或近似解时较为困难，在过去二、三十年中，有限元法和边界元法被广泛应用于沉桩机理的分析研究中，大量学者对桩土作用进行了有限元研究[8-9]。使用有限单元法能较好地模拟圆桩贯入过程中产生的挤土效应，分析土体的水平位移和垂直隆起高度，且模拟出的结果与现有试验的结论取得较好的一致性，在应用中，有助于减少和预防实际工程中的危害。

本研究运用RITSS大变形有限元数值程序，模拟圆桩贯入黏土的过程，得出贯入过程中桩周土体位移的变化规律，分析不同贯入深度和土体强度对挤土效应的影响。

1 方法

1.1 RITSS 大变形有限元方法

大变形有限元分析方法（LDFE）主要分为欧拉法（Eulerian）、拉格朗日法（Lagrangian）和任意拉格朗日欧拉法（Arbitrary Lagrangian-Eulaerian，以下简称 ALE）三种。其中任意拉格朗日欧拉法[10-11]将拉格朗日法和欧拉法结合在一起，克服了两种方法各自的缺点，ALE法中网格可以独立于物质和空间位置自由地运动，在发生较大变形时，网格不发生较大的扭曲。1998年Hu等[12]针对固体大变形问题提出了基于小变形模型计算的网格重划分和插值方法（Remeshing and Interpolation Technique with Small Strain Model，简称RITSS），该方法是任意拉格朗日欧拉法的一种。Tian等[13]优化了RITSS，提出了一种更简单、更实用的方法，通过使用ABAQUS内置程序进行插值和重划分，解决了网格重划分和插值需要在特定服务器上进行的问题。

RITSS方法的主要步骤为：1）生成初始网格；2）施加小位移或荷载进行小变形计算，提取计算结果（应力场和其它与土体特性相关场变量）；3）重划分、优化网格，得到更新边界之后的新网格对应的单元与节点信息；4）在第2步获得的应力和土体特性相关场变量中进行插值运算；5）检查位移荷载或力荷载是否达到所需条件，若不满足，则重复1～4计算步骤，若满足则结束计算。

RITSS方法能避免大变形中网格扭曲，网格会不断变化更新以确保重点关心的结构物周围的网格一直处于高精度和密度状态，使得计算顺利进行，获得高精度计算结果。目前，RITSS方法被认为是解决海洋岩土中贯入大变形问题的一种有效方法，得到了广泛应用[14-15]。

1.2 几何参数

本研究运用RITSS大变形有限元方法，模拟直径为D的圆桩贯入均质海洋软黏土过程中发生的挤土效应，分析其对临近土体的扰动，从而评估沉桩贯入对临近已有桩基础的影响。贯入深度为Lz，观测点深度为z，观测点距桩轴线距离为r。E、υ和Su分别为土体的弹性模量、泊松比和不排水抗剪强度。土体参数见表1。

计算模型采用二维轴对称模型，土体区域高宽均取50D以消除边界效应，模型的左右边界和上下边界分别采用铰约束和滚动约束。有限元网格由具有3个高斯积分点的六节点三角形单元构成，为保证计算精度，越靠近结构周边区域网格越密，其最小单元尺寸为hmin=0.05D。桩土接触面用Herrmann提出的一种弹塑性节点约束关系进行模拟，该接触法向约束关系为“硬接触”[16]，两接触面法向方向不允许穿透，接触面的极限抗滑强度为αSu，其中α为桩模与土间的摩擦系数。土体采用符合Tresca屈服准则的弹塑性材料的摩尔库伦模型模拟。结构物与土体接触与脱开通过预设准则进行判别与处理。本研究中处理准则设置为临界位移dcri=0.05hmin，其中hmin为最小网格尺寸。当材料线与桩身间的距离小于dcri时，认为两者相接触，自动断开材料线并进入分区动态管理。不同贯入阶段的模型网格见图1。

表1 土体参数Table 1 Soil parameters

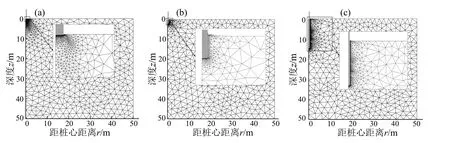
图1 模型网格Fig.1 Mesh of the model

2 结果与分析

2.1 模型验证

基于圆锥贯入仪与圆桩的相似性，将RITSS的计算结果与已有圆锥贯入仪计算及试验成果进行对比，以验证所用大变形有限元软件的可靠性[17-24]。锥体从泥面开始贯入，土体的刚度指数Ir分别设置为50、150、300和500，土体强度Su=10 kPa，D=0.035 7 m，计算承载力系数Nkt。

图2和图3为本研究方法与Baligh等[17]的应变路径法，Teh等[20]的应变路径法和混合应变路径法，Yu等[23-24]的孔穴扩张法和稳态有限元法，Van den berg[21]、Lu等[19]、Liyanapathirana[18]、Walker等[22]的大变形有限元法的结果对比。

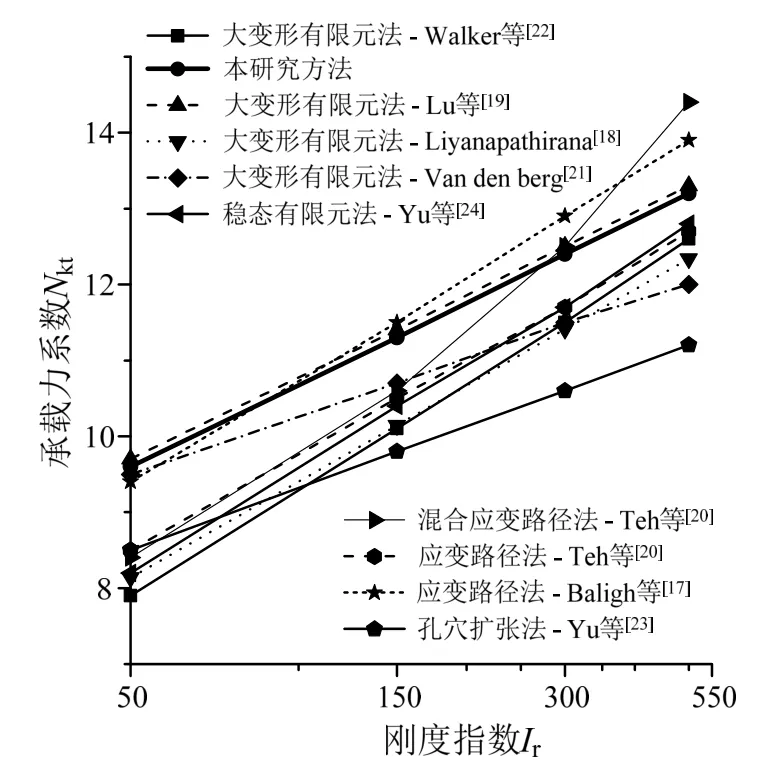
图2 光滑锥体（α=0）模型验证Fig.2 Comparison of cone factor Nkt with previous solutions for the smooth cone (α=0)

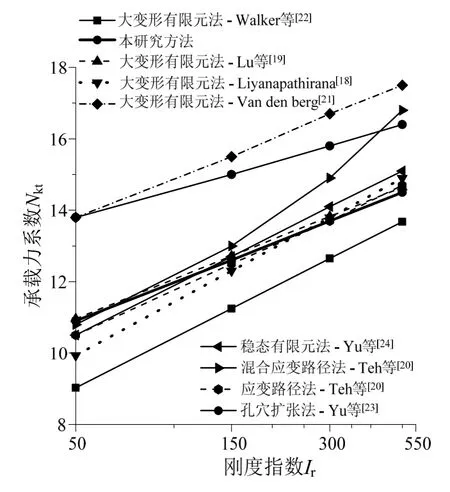
图3 粗糙锥体（α=1）模型验证Fig.3 Comparison of cone factor Nkt with previous solutions for the rough cone (α=1)

由图2可见，对于光滑椎体，本研究方法与Baligh等[17]的应变路径法和Lu等[19]的大变形有限元法结论一致。图3显示，对于粗糙椎体，本研究方法所得结果与Teh等[20]的应变路径法、Yu等[24]的稳态有限元法和Lu等[19]的大变形有限元法的结果一致。可见，本研究所用软件计算结果与已有研究结果取得了较好的一致性。

2.2 贯入深度对桩周土体水平位移的影响

圆桩贯入土体的过程中，桩周土体发生严重扰动，土体表面会发生明显隆起，桩侧土体发生水平向位移。距离圆桩越近，土体受到的扰动越大，位移越明显。由土体流动模型（图4）可见，在浅层贯入区域（d/D=1.3），桩底部土体发生旋转失效，诱发桩底部土体向上运动，从而导致桩身附近表层土体隆起显著增加。随着贯入深度的增加（d/D=10），土体流动规律发生变化，桩底部土体主要向侧向运动，这样会诱发离桩较远处的地基表面发生隆起，由于土体隆起范围扩大，而贯入土体的桩的体积增量固定，因此增加的隆起位移小。

改变圆桩贯入深度Lz以研究贯入深度对桩周土体水平位移的影响，土体重度γ′=6 kN/m³，黏聚力c=20 kPa，桩体直径D=1 m，其余参数见表1中组Ⅰ-1～Ⅰ-4。图5(a)、(b)、(c)中观测点距圆桩中轴线的水平距离r分别为1R、2R、3R（R为圆桩半径），纵坐标为观测点深度z，横坐标为观测点的水平位移δr。由图5可见，桩长较短，贯入深度较小时，距桩心1R处土体的水平位移随深度的增加而快速增加，距桩心2R和3R处土体的水平位移随深度的增加呈现先减少后快速增加的规律。由于地表的土体被桩向外挤出，桩周土的水平位移δr随距圆桩中轴线的距离r的增大而减小，越靠近桩的地方，土体受到的扰动越大，挤土效应越明显，该处水平位移随深度增加而快速增加，这与李家华等[3]运用ABAQUS进行数值模拟得出的结论一致。对不同的贯入深度，水平位移极值均出现在桩底部，这是因为桩端土体受扰动程度最强，土体位移变形最大。

图4 土体流动模型Fig.4 Soil-flow mechanism

当贯入深度Lz=5 m时，水平位移在深度z=5 m处达到最大，此后迅速衰减，影响范围深10 m；当贯入深度Lz=10 m时，水平位移在深度z=10 m处达到最大，此后迅速衰减，影响范围深15 m，由于桩底处土体受扰动较大，因此贯入深度较小时，水平位移均在桩底处达到最大。当贯入深度Lz分别为15 m和20 m时，水平位移均在深度z=12 m处达到最大，在桩底（深度分别为15 m和20 m处）开始迅速衰减，影响范围深度分别为20 m和25 m，这是由于在土颗粒间的相互作用下，桩周土水平位移有极值，达到其极值后，桩底下部桩周土体水平位移随深度的增加而快速衰减。

对于深层贯入的圆桩，在贯入深度达到Lz/D=6后，土体的水平位移随深度的增长而趋于稳定，在Lz/D=12时，桩周土的水平位移达到最大，与Hwang等[25]观测得出的该距离（10D）相近。桩在贯入过程中的土体流动显示，圆桩贯入时影响范围集中在桩段，在桩端下部影响范围外的土体扰动相对较小，因此，当贯入深度达到Lz/D=12后，随着圆桩贯入深度和土体深度的增加，桩周土的水平位移都不再增加。

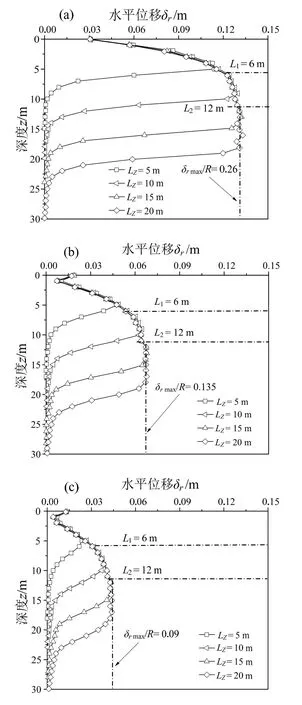
图5 贯入深度对水平位移的影响Fig.5 Effect of penetration depth on lateral displacement

2.3 贯入深度对桩周土体隆起高度的影响

改变圆桩贯入深度Lz以研究贯入深度对桩周土体隆起高度的影响，土体重度γ′、黏聚力c、桩体直径D取值同2.2节，其余参数见表1中组Ⅱ-1～Ⅱ-4。由图6可见，由于地表的土体被桩向外挤出，桩周土体的隆起高度δz随观测点距圆桩中轴线的水平距离r的增大而减小，越靠近桩的地方，挤土效应越明显，隆起高度变化越快。桩在浅层贯入区域及深层区域的土体流动均显示，其在靠近桩的地方土体向上流动的位移最大。贯入深度越大，由于圆桩排开的土体量增多，相同深度处的土体隆起高度越大。

在距圆桩中轴线距离r=Lz范围外，土体隆起量近似为零，这是由于随着土体与距离圆桩中轴线的距离r的增大，超负荷应力衰减，桩身对土体的扰动越来越小，故笔者认为圆桩对桩周土体垂直隆起的影响范围为1倍桩长左右，且越靠近桩，挤土效应越明显，在远离桩的方向上土体隆起高度的衰减越快。随着贯入深度的增加，影响范围逐渐增加，桩周土体隆起高度累计增加越多。土体隆起规律与Zhao等[26]运用有限元软件模拟桶桩在黏土中的贯入过程得到的土体隆起规律一致。

图6 贯入深度对隆起高度的影响Fig.6 Effect of penetration depth on soil heave height

2.4 土体强度对桩周土体水平位移的影响

改变土体弹性模量E以研究土体强度对桩周土体水平位移的影响，土体重度γ′、黏聚力c、桩体直径D取值同2.2节，其余参数见表1中组Ⅲ-1～Ⅲ-4。由图7可见，土体强度对桩周土体水平位移的影响不大，主要体现在深度为1～10 m的土体处，在这段深度（10D）内，土体强度越小，距桩心越近，相同深度处的土体水平位移越大；在此范围外，由于选用的是饱和黏性土，贯入过程中不排水，土体体积几乎不发生变化，土体强度对桩周土的水平位移基本没有影响。这与Zhou等[27]运用有限元软件研究PCC贯入饱和黏性土时获得的结论相同。

2.5 桩周土体水平位移及隆起高度计算公式

桩周土体水平位移δr受土体的几何位置影响较大（即深度z和距桩轴线的水平距离r），水平位移最大值受土体弹性模量E的影响较小，可以忽略。因此，本研究利用大变形有限元计算结果拟合出桩周土体水平位移δr受贯入深度Lz和距桩轴线水平距离影响的函数关系式（式1）。将公式计算结果与数值模拟结果进行对比（图8），在最大值处基本吻合。

桩周土体隆起高度δz受土体距桩轴线的水平距离r以及圆桩的贯入深度Lz影响。拟合出桩周土体隆起高度δz受贯入深度Lz和距桩轴线水平距离r影响的函数关系式（式2）。将公式计算结果与数值模拟结果进行对比（图9），结果基本吻合。

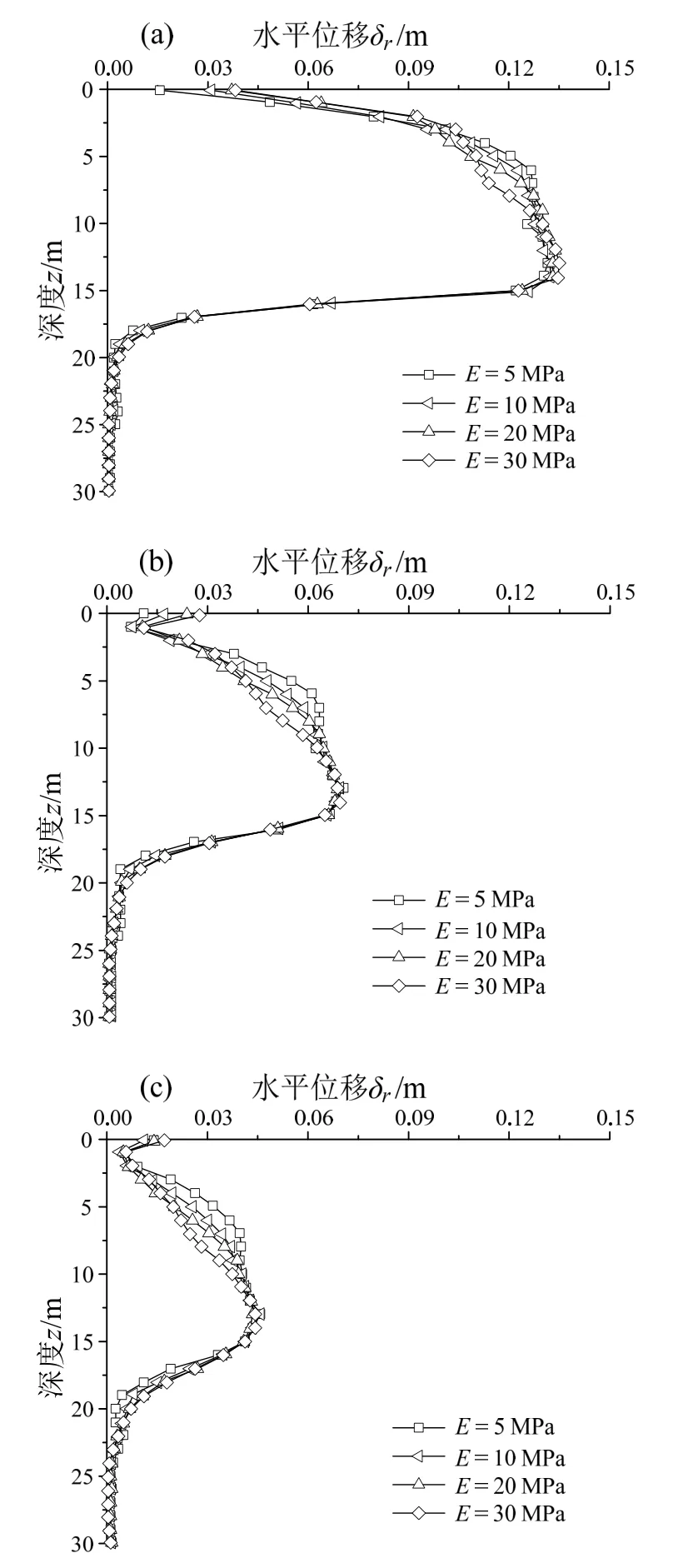
图7 土体强度对水平位移的影响Fig.7 Effect of soil strength on lateral displacement

图8 水平位移预测公式Fig.8 Prediction formula of horizontal displacement

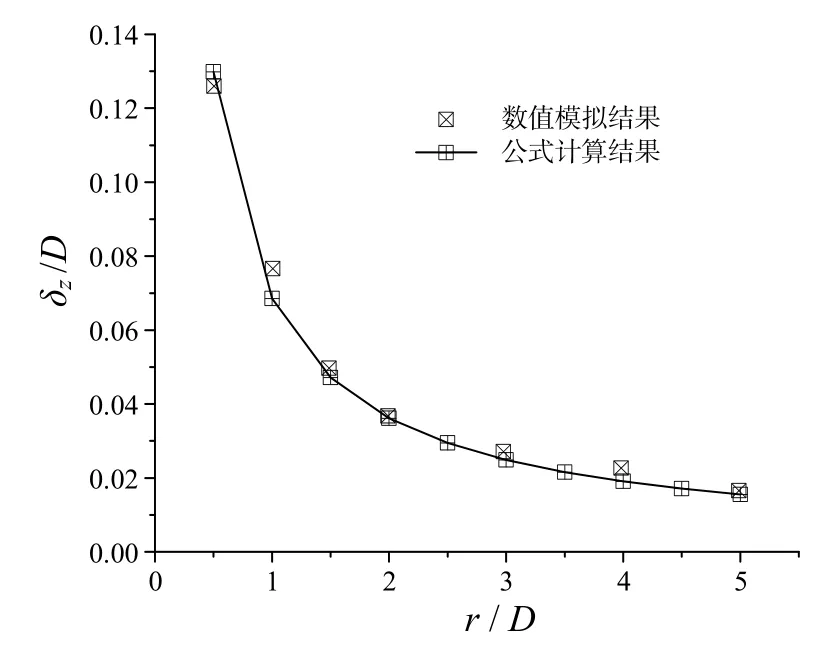
图9 桩周土体隆起高度预测公式Fig.9 Prediction formula of soil heave around pile

3 结论

为研究圆桩贯入海洋黏土过程中发生挤土效应对临近桩基础的影响，本团队运用RITSS大变形有限元方法模拟圆桩贯入饱和黏土的过程，考虑圆桩贯入深度Lz、桩周土体距圆桩中轴线距离r、土体深度z以及土体弹性模量E四个因素，得出以下结论：(1)在贯入深度Lz/D＞6时，桩周土体的水平位移随深度的增长而趋于稳定，当Lz/D=12时桩周土体的水平位移达到最大，在距桩1R～3R处，桩周最大水平位移为0.26R。(2)桩周土体的水平位移随距圆桩中轴线的距离的增大而减小，距圆桩中轴线越近，水平位移随深度增长越快。(3)贯入深度越大，距圆桩中轴线越近，相同深度处的土体隆起高度越大，在距圆桩中轴线距离r=Lz范围外，土体隆起量近似为零，本研究认为圆桩对桩周土体垂直隆起的影响范围为1倍桩长左右。(4)拟合出桩周土体水平位移和隆起高度的计算公式，能够预测沉桩对临近土体扰动的影响范围，能较为准确地评估多桩系统中沉桩对临近桩基础的影响。