时域下空间曲线曲率及挠率问题的研究

许 飞，刘翠香，闵祥娟，单彩虹，曹贻鹏

（陆军装甲兵学院基础部，北京 100072）

0 引言

在战术弹道导弹拦截领域，传统的基于视线（LOS）角速度的比例导引及其变形，以其易于实现、高效而得到广泛的应用［1-2］，其在本质上是在目标不机动、系统无延时、控制能量不受约束情况下产生零脱靶量和控制量的平方积最小的制导律［2］。但现代战争中的拦截目标机动性强、制导环境恶劣、飞行轨迹无法准确预测等现实问题，也对导引律的设计和应用提出了更高的要求，针对这些问题，相继提出了最优制导、自适应制导、微分对策及神经网络制导等大量的现代制导规律，但真正在实际中应用更多的是如比例导引及其变形的古典制导律［3］。

空间域下拦截弹的制导问题可抽象为空间曲线问题，是微分几何主要的研究对象，曲线性态在局部上完全由曲率和挠率所决定，为此，可通过实时调整曲率和挠率的取值，实现拦截弹的路径预测和规划。本文以拦截弹的实时位置信息为原点，建立活动标架，结合拦截弹的实时速度建立关于弧长的Frenet 公式，并将其转化为时域上的Frenet 公式，根据视线运动方程和弹目相对运动方程推导了曲率和挠率指令表达式，从指令表达式上看，相关变化量易于测量，便于仿真，是对拦截弹路径规划及有效制导的有益探索。

1 空间曲线的活动标架和Frenet 公式

1.1 弧长域下的空间曲线及Frenet 公式

拦截弹制导策略问题可抽象化为E3上具有一个自由度的质点运动问题，其向量形式的参数方程可表示为［4-5］

1.2 时域下的空间曲线及Frenet 公式

在传统的拦截弹制导策略研究中，通常采用的独立参数为时间变量t，与采用弧长参数s 之间具有关系式［6-7］

联立式（12）～式（14），可得到具有形式（1）的时域下的Frenet 公式

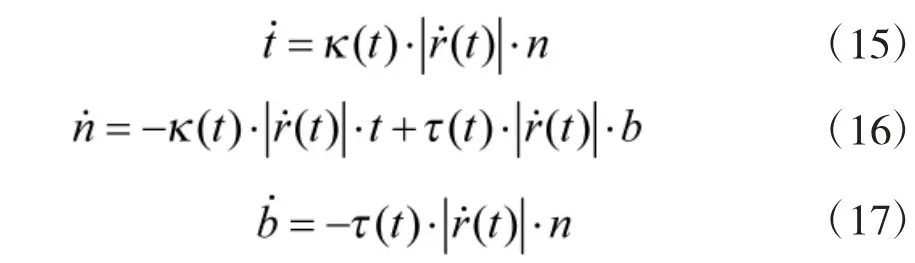
通过对式（12）～式（14）的简单计算，可得空间曲线方程在时域下的曲率和挠率计算公式

式（5）、式（6）、式（18）、式（19）即为弧长域及时域下的曲率、挠率表达式，下面将对实际问题进行几何建模，推导能够应用于实际的曲率和挠率公式，从而用于拦截弹制导的路径规划。

2 拦截弹制导的几何模型建立

2.1 视线运动方程的推导

图1 拦截弹活动标架

根据视线旋转的几何关系，可建立关于视线运动的Frenet 公式

2.2 拦截弹运动方程的推导

2.2.1 弹目运动方程的推导

在本节中，下角标T，M 分别表示目标弹和拦截弹，弹目相对运动的几何模型如图2 所示，其中，rM是拦截弹的有向距离，vM为拦截弹速度矢量，大小为vM，tM，nM是拦截弹运动的方向切向量和主法向量，r 是弹目的有向距离，θM是弹目视线角，φM，φM是拦截弹运动方向与弹目视线和其法向量的夹角，同时目标弹也有上述相关几何描述，如图2 所示。

图2 弹目相对运动几何模型

在2.2.1 节中得到了弹目视线的切向量、主法向量及副法向量的表达式（22），其形式完全由拦截弹与目标弹的速度及实时位置信息所决定。

2.2.2 空间曲线曲率指令的推导

对式（21）进行变形可得

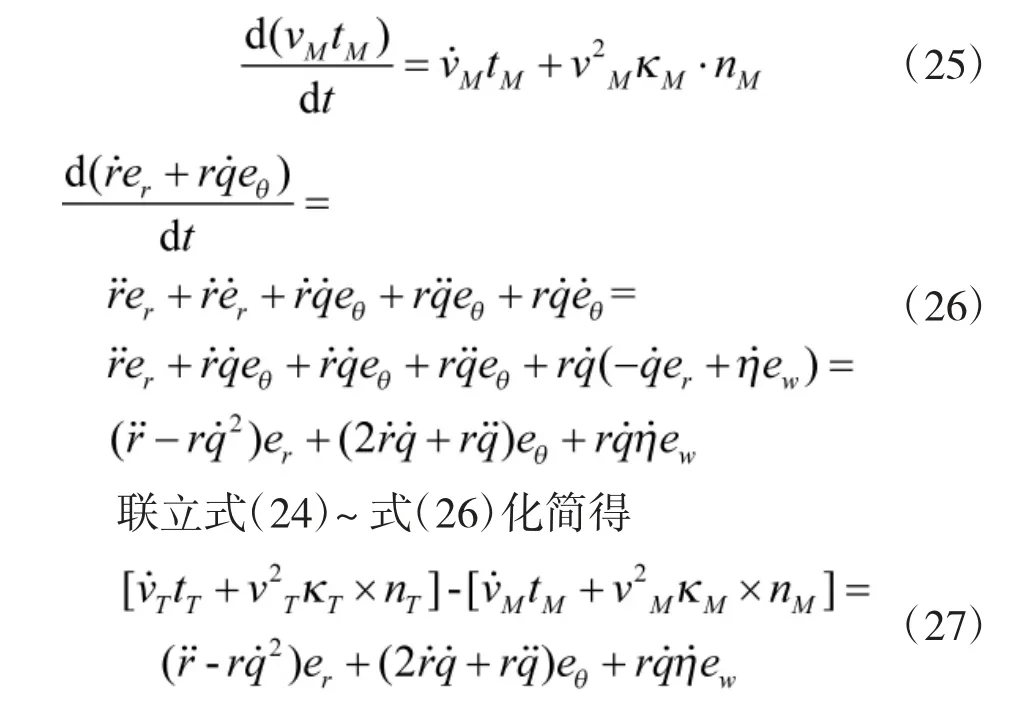
由于曲率用于控制拦截弹的转向，其方向与eθ同向，则可对式（27）两端同乘eθ得

2.2.3 空间曲线挠率指令的推导

在2.2.2 与2.2.3 节中详细地推导了拦截弹制导的曲率和挠率指令表达式，其中，曲率指令表达式又分为恒速和变速两种拦截方式，适用范围更广，且表达式的各个变量均是可测的，易于后续模拟仿真的实现。

3 结论

拦截弹路径规划及制导过程实际上就是空间曲线性态研究问题，本文通过弧长域下的Frenet 公式转化到时域下的Frenet 公式，又进一步推导了在恒定速度拦截和变速拦截两种情况下的曲率和挠率的指令表达式，从结果上看，指令表达式的各量都可以根据弹目实时位置信息和速度信息求得，后续将依托曲率和挠率的指令表达式进行离散化处理，利用MATLAB、PYTHON 相关软件进行模拟仿真。