卡尔曼滤波补偿在潜载光电跟瞄中的应用*

张雨恒，刘宗凯，周本谋，刘禹铭

（1.南京理工大学瞬态物理国家重点实验室，南京 210094；2.南京理工大学自动化学院，南京 210094）

0 引言

潜载光电设备在目标的捕获跟踪阶段，由于艏摇、纵摇、横摇的扰动，跟踪误差会增大。只对视轴稳定采取优化，无法完全消除自身扰动的影响，甚至会导致跟踪失败。视轴优化中，影响光电跟踪系统的主要因素除了目标的运动及平移，还有目标的旋转运动。文献［1］通过对脱靶量的滤波预测进行延时补偿，提高光电设备的跟踪精度。文献［2］针对舰载光电设备的扰动进行了建模，计算出船摇扰动的角速度作为前馈补偿，减小了跟踪误差。文献［3］使用改进的Singer 模型的卡尔曼滤波，研究了一种对非线性状态目标更有效的跟踪算法。Singer 模型相较于传统的CA（匀加速）和CV（匀速度）机动模型，将目标的机动认作是时间相关的有色噪声序列而非统计独立的白噪声序列作用的结果，对应于目标包含匀速和匀加速之间的运动，较CA 和CV 模型有更大的目标机动模式覆盖范围［4］。本文在潜艇与地面坐标的转换基础下，对整个随动系统中的粗跟踪系统，应用PID 控制以及通过Singer 模型的Kalman 滤波的方法得出前馈补偿，并结合精跟踪FSM 快速反应镜控制系统，完成整个光电设备的复合控制。

1 设计原理

1.1 坐标转换

潜艇姿态可以用潜艇甲板坐标系相对于大地水平坐标系的摇摆角度（艏摇角αH，纵摇角αP，横摇角αR）来表征。目标点在大地坐标系中的方位角为A，俯仰角为E。由于CCD 采样周期较小，单位时间内潜艇平移造成的方位和俯仰角度的变化也较小，相对于艇摇运动，可以忽略平移运动的影响。下面引用文献［4］对潜艇光轴坐标的转换。

仅在发生艏摇、纵摇以及横摇扰动下，目标点G（x，y，z）在大地坐标系中的方位角和俯仰角可以通过αH、αP、αR逐一解算到下一时刻视轴坐标系中，将大地坐标系（X，Y，Z）下目标点的坐标转换到潜艇坐标系（Xd，Yd，Zd），需要经过3 次坐标变换：1）艇体绕OZ 轴以角速度ωH转动αH（艏摇角）；2）艇体再绕OY 轴以角速度ωP旋转αP角（纵摇角）；3）艇体再绕OX 轴以ωR旋转αR（横摇角），如图1 所示。

这3 次摇摆姿势解算可以写成如下矩阵形式：

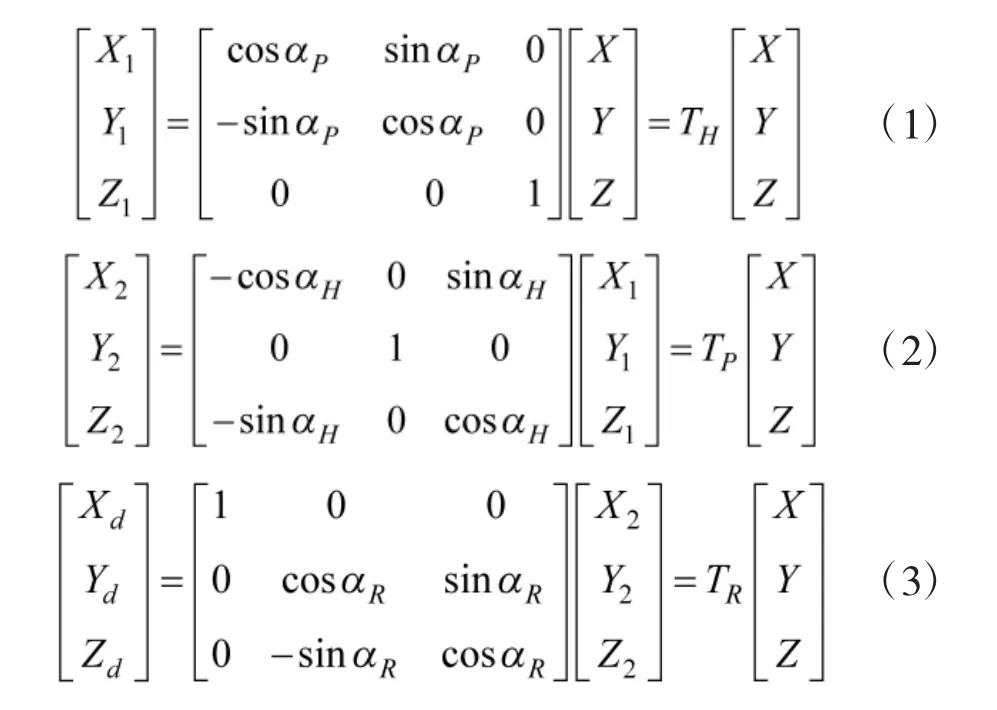
经过3 次坐标变换得出艇体坐标为：

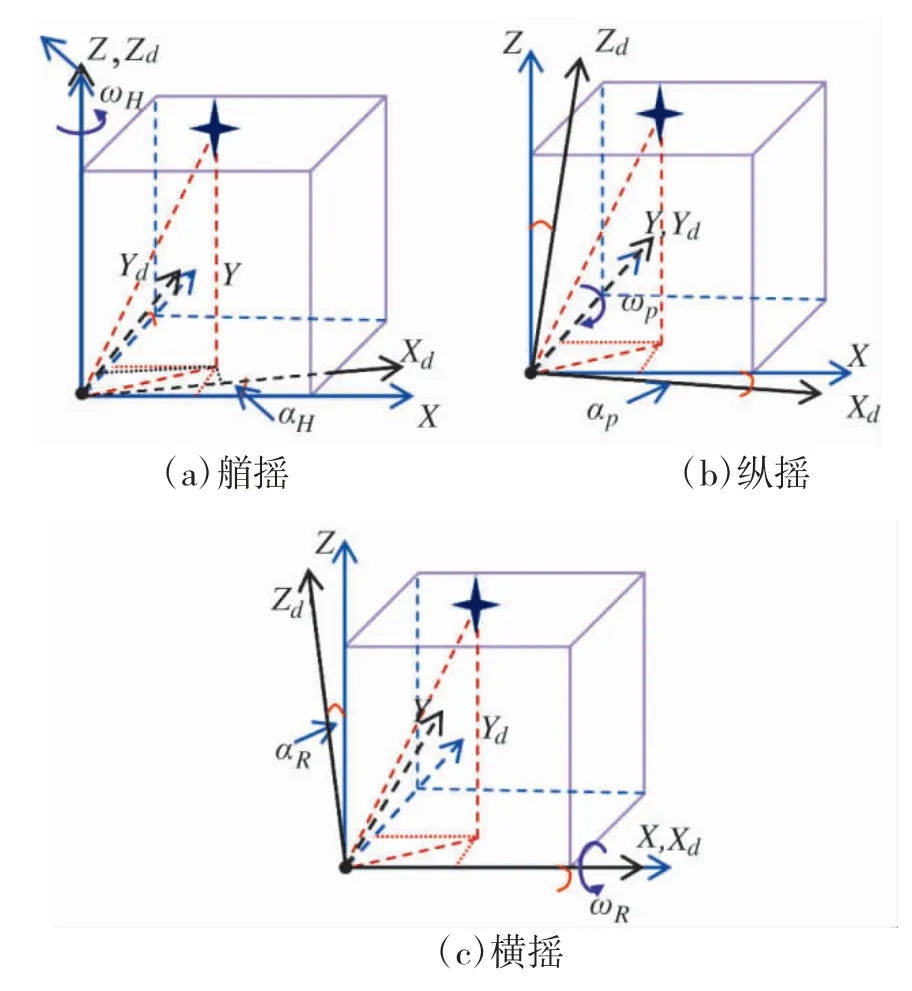
图1 坐标转换示意图

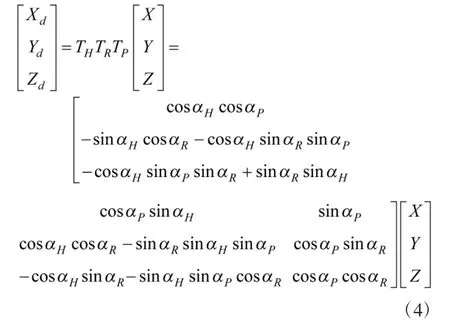
将潜艇光轴坐标系下的直角坐标点（Xd，Yd，Zd）转换为方位和俯仰角（Ad，Ed）［5］：

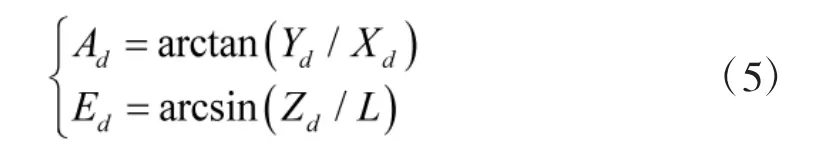
式中，L 为斜距，即探测点与目标之间的距离。联立方程可得：

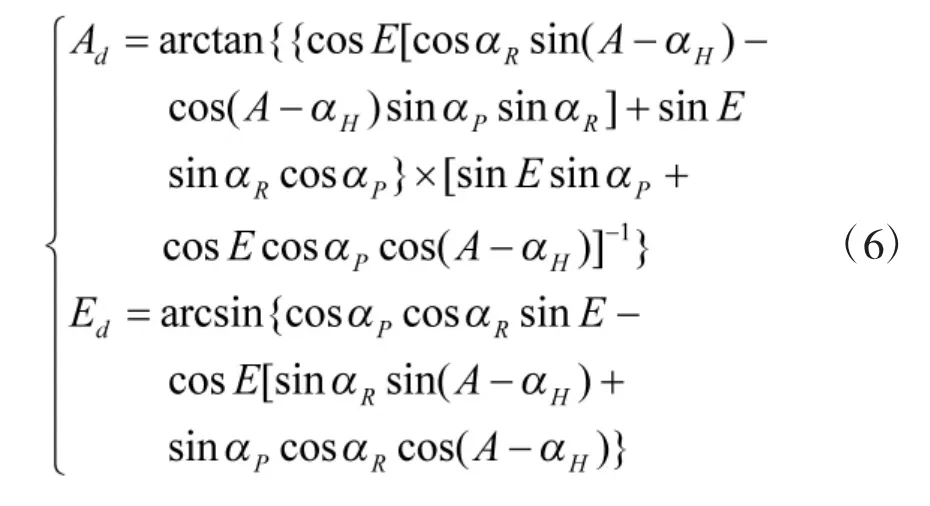
1.2 Singer 模型的Kalman 滤波前馈控制原理

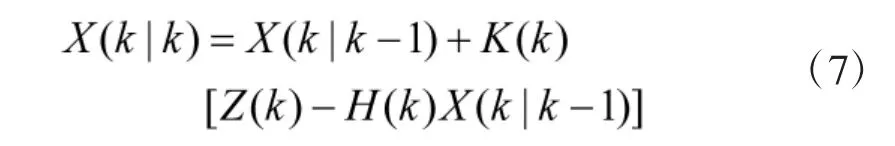
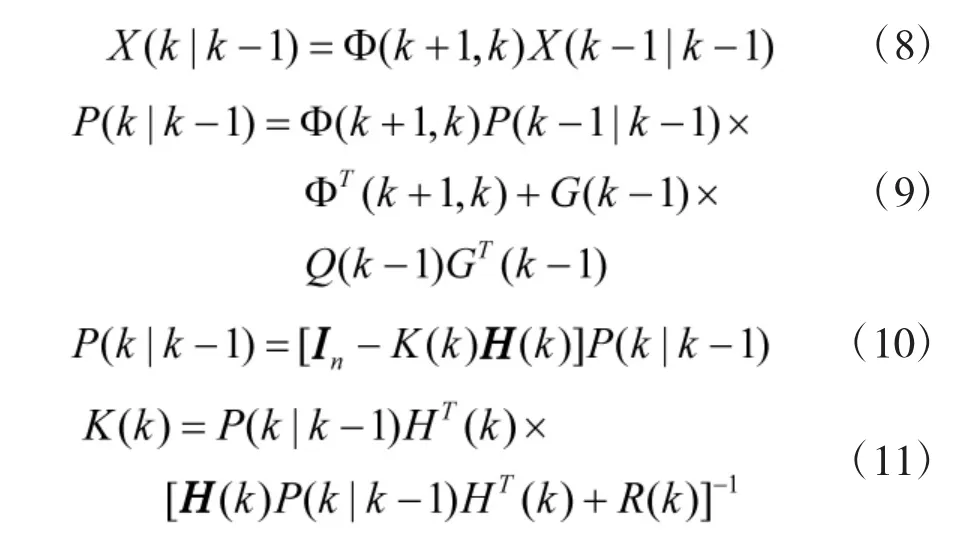
Kalman 滤波的基本方程为其中，X（k）为n 维目标状态向量，Z（k）为n 维目标量测向量，In为n 维单位矩阵，G（k），H（k）以及Φ（k）为常数矩阵用于表示状态方程。

CV 机动模型假设运动目标为匀速直线运动的状态，即目标的加速度值为0；CA 机动模型假设运动目标为匀加速直线运动的状态，即目标的加速度的导数为0，但由于干扰的存在，CV 模型中目标的加速度不能维持在零值，CA 模型中目标加速度的导数不能维持在零值，因此，在这两个模型下都采用均值为0 的高斯白噪声表示噪声的变化。

在跟踪圆形运动时，CA 模型考虑了目标运动的加速度成分，在拐弯时跟踪结果明显好于CV 模型。跟踪蛇形运动时，由于加速度的噪声分布已经不再满足CA 模型的假设条件，所以在拐弯处的误差较大。Singer 机动模型的噪声则假设为有色噪声，这一般更符合实际噪声，所以在处理圆形以及蛇形机动时有更好的效果。

Singer 时间相关模型提出机动目标加速度的时间相关函数为指数衰减形式［6］：

2 前馈控制系统的实现

2.1 粗跟踪控制系统介绍

粗通道主要是由直流力矩电机和转台构成，数学建模和仿真时，认为方位和俯仰角传递函数一致。首先，对直流力矩电机进行建模，这里将跟踪转台作为负载，将其惯量折算到直流力矩电机的转轴上，忽略电流的波动性，则电流为直流，直流力矩电机可近似为线性元件。由电机工作原理和电枢回路电压平衡方程可以推导出直流力矩电机的传递函数，仿真框图如图2 所示。

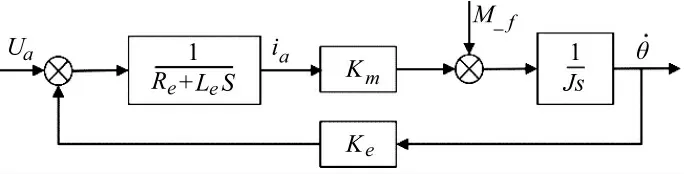
图2 力矩电机数学模型

Ua为电机的控制电压输入，Re、Le分别为电枢的电阻和电感，ia为电机的驱动电流，Km、Ke分别为转矩灵敏度系数和反电动势系数，Mf为扰动力矩，J为电枢转动惯量。

整个控制系统控制回路的建模是力矩电机电压和角速度之间的传递函数，需经速度环和位置环的转换。为了提高响应速度，在速度环中采用PI 控制器，位置环中采用PID 控制器［7-8］。

通过Kalman 滤波的基本方程，Singer 运动模型的状态方程的离散化表示为

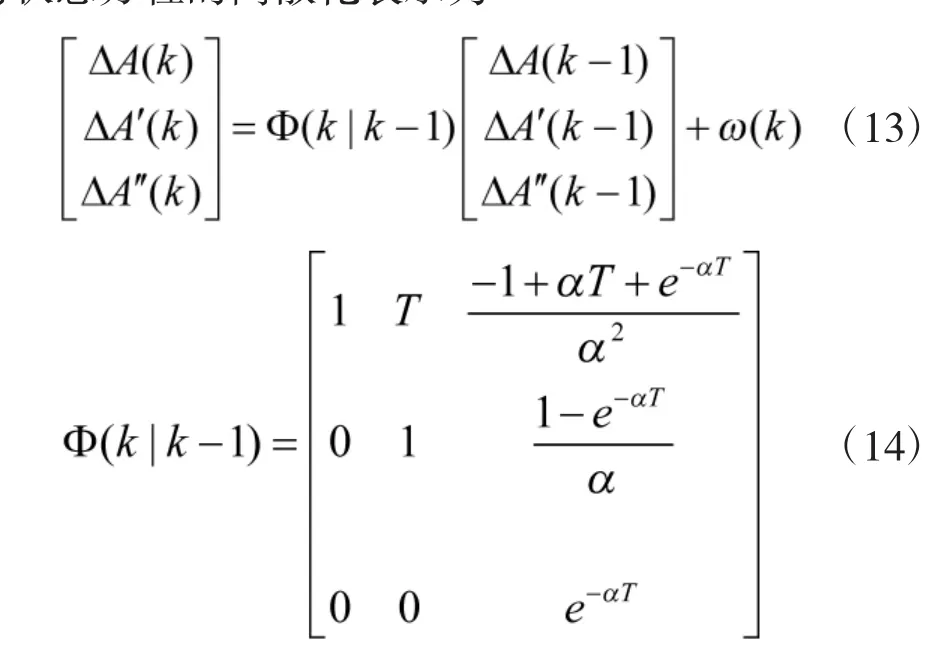
其中，T 为采样周期，Q 为系统噪声的方差矩阵［9］，ω（k）均值为0。

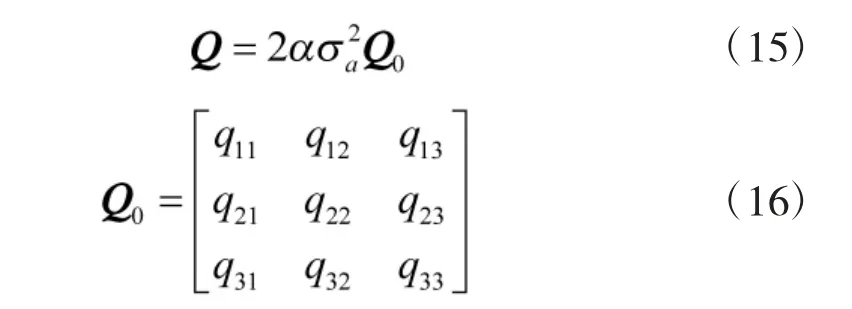
其中，

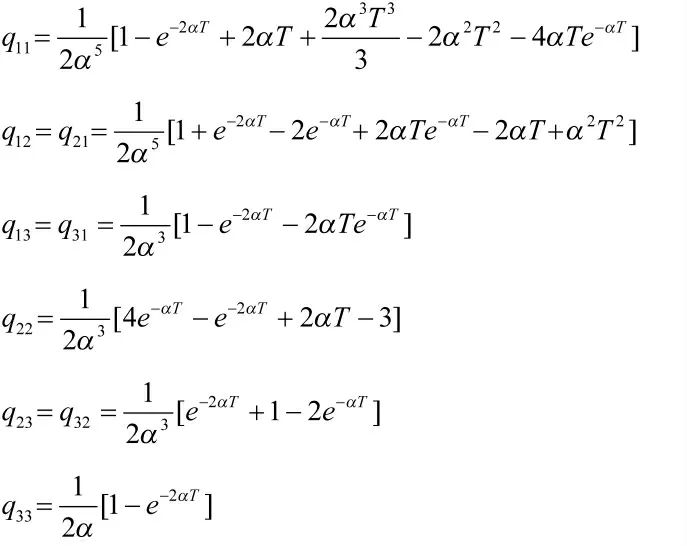
以方位角控制回路为例，随动系统和Simlink仿真图如图3 所示。

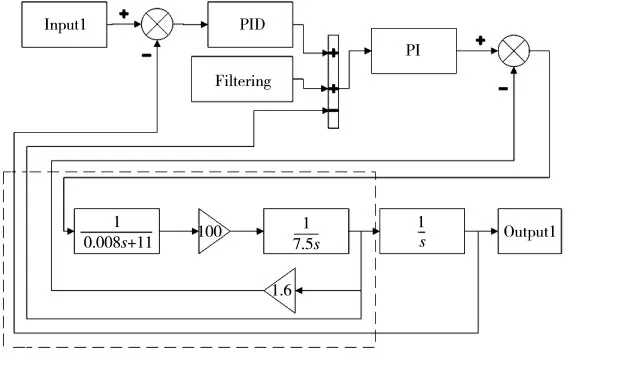
图3 粗跟踪系统仿真图

图中PID 控制器所在环路为位置环，PI 控制器所在环路为速度环，Input1 输入包含了脱靶量信息，Filtering 输入的是滤波之后的扰动数据，下半部虚框部分是实验所选用电机的传递函数。粗跟踪控制系统通过对输入的船摇扰动数据和当前方位角合成的扰动输入进行滤波，得到滤波之后的数据，再结合脱靶量信息反馈给控制系统，得到粗跟踪系统的跟踪误差。

2.2 精跟踪FSM 快速反应镜控制系统介绍

快速反应镜的跟踪特性是当粗跟踪输入的跟踪误差足够小时，精跟踪系统中的出光光路才能够准确。仿真研究采用的FSM 快速反应镜是德国PI公司的P-T04K010 压电陶瓷偏摆镜，快速反应镜的4 个运动支点在搭载镜片之后，可以实现俯仰和倾斜两个自由度的微调。物理摆角幅度为±12.5 mrad，而P-T04K010 精度闭环精度为5 μrad。实验中通过频谱仪测出的FSM 快反镜系统闭环状态下的频响曲线，其闭环传递函数［10-11］：

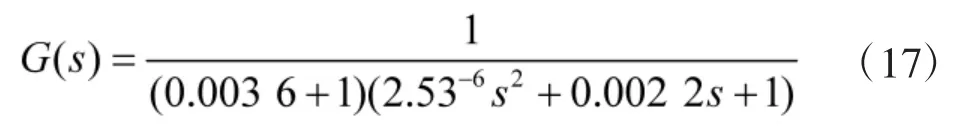
仿真系统图如图4 所示。

图4 精跟踪系统仿真图

快速反应镜仿真系统中的输入Input2 为图2粗跟踪的误差Error，Output2 为输出。通过PID 控制器控制驱动元件的运动来实现快速反射镜的偏转，凭借其质量轻、响应速度快的特点，可以及时修正跟踪误差，减小转台跟踪残差。

3 仿真分析

根据式（2）解算所得方位角以及俯仰角脱靶量输出曲线如图5 所示。

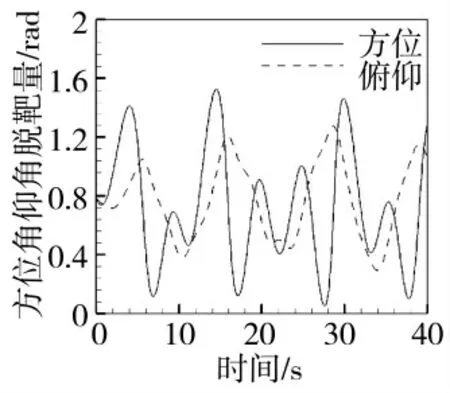
图5 方位俯仰角脱靶量

仿真中，粗跟踪通道的工作频率为20 Hz，由于有相机图像分辨率误差、信号处理误差等，通常将仿真采用的量测噪声均方差设为4.85''，系统噪声由式（14）与式（15）所得。

下页图6 中脱靶量的输入为2 s，前幅值为0，2.05 s 后幅值为1 rad 的阶跃信号，对Singer 模型以及CA 模型进行了对比，阶跃响应仿真图以及跟踪误差仿真结果见图6。

可以看出，Singer 模型下的误差结果相较于CA模型下的跟踪误差，拥有更快的响应速度并且能够更快地收敛，Singer 模型在大约2.9 s 时就已经稳定，而CA 模型则在大约3.2 s 时才稳定。图中稳态误差出现较大波动主要原因是量测噪声，这样的残差可以由精跟踪控制系统减小。

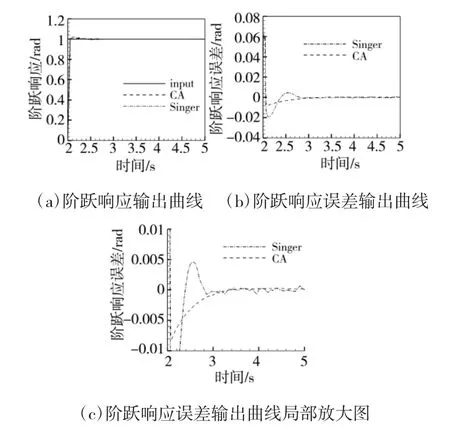
图6 粗跟踪控制系统阶跃响应

在图7 的仿真结果中，输入信号为图5 中的方位角扰动量合成的脱靶量信息，前馈补偿为对纯扰动量滤波得到的速度补偿。在数值仿真下对光电控制系统是否有速度前馈进行了对比，在没有速度前馈时，方位和俯仰的跟踪误差最大可达±0.004 5 rad；在加入滤波的速度前馈之后，方位跟踪误差最大约为±0.000 9 rad，俯仰跟踪误差最大约为±0.001 rad。可以看出，经过卡尔曼滤波补偿控制系统的跟踪误差明显小于无补偿的控制系统。

图7 粗跟踪误差对比

4 结论

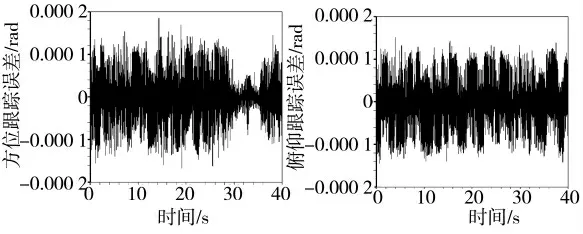
图8 复合控制跟踪输出误差

本文以潜载光电控制系统为研究对象，通过Matlab 仿真分析了艏摇、横摇、纵摇3 种运动对控制系统的影响。在潜艇坐标转换基础上，对潜艇扰动进行Singer 模型下的Kalman 滤波，将滤波预测到的速度值前馈到速度环，提高复合轴控制的跟踪精度。仿真实验以方位角为例，表明扰动经由坐标变换以及粗精复合控制之后，能够有效减少误差，相较于CA 模型，Singer 模型拥有更快的响应速度和收敛速度。粗通道方位角跟踪误差在未加入反馈时约为±0.004 5 rad，在加入反馈之后跟踪误差约为±0.000 9 rad，复合轴控制跟踪误差范围减少至±0.000 2 rad。