通用防空反导火力优化分配方法*
2021-02-03王玉茜
王玉茜,张 栋
(1.江南机电设计研究所,贵阳 550009;2.西北工业大学航天学院,西安 710072)
0 引言
未来联合防空反导作战环境下,通常是多个火力单元对多个目标实施火力拦截。对目标实施高效拦截,必然要考虑对不同目标的火力如何进行分配,即通常所说的目标分配或火力分配。由于各火力单位对目标的毁伤效能以及诸目标本身价值及威胁性等的不同,火力分配受到多种约束条件的限制,火力单位对目标的分配也存在多种方案。火力单位最优分配的任务就在于发挥诸火力单位的整体协调优势,寻求在给定约束条件下,总的射击效果最好的分配方案[1]。在火力分配方面,文献[2]研究了面向多目标优化火力分配问题的前瞻式边际贪婪算法。文献[3]提出了一个结合贪婪规则的蚁群算法求解单目标火力分配问题。在多平台协同防空武器调度方面,国内外关于这方面的研究较少。文献[4-5]提出了多平台协同防空武器调度的方案,并建立了调度数学模型。文献[6-7]基于资源调度模型,建立了协同防空武器的调度模型,并提出了相应的调度模型与算法。
本文对防空反导作战火力分配问题进行深入分析,考虑到防空和反导问题的差异性,详细建立了通用优化模型,并针对其特点设计了优化算法。
1 区域防空反导火力分配原则
在区域防空反导作战中,火力任务规划遵行的主要原则是:优先射击高威胁目标,整体上达到最优分配,同时要考虑各个火力单元的杀伤效能及武器消耗,以达到最大作战效能和防御效能。具体分配原则如下:
原则1:优先响应人工干预命令;
原则2:威胁大的目标优先分配;
原则3:目标分配火力单位必须满足资源约束和空间约束条件;
原则4:当弹道导弹类目标的预测弹道通过两个及两个以上火力单位火力重叠区时,优先采用集火射击进行拦截,即将目标分配给两个或两个以上可分配的火力单位;
原则5:每个目标尽可能都分配到至少一个火力单元。
2 火力分配模型设计
针对上述分配原则,设计优化分配模型约束条件和目标函数。
2.1 约束条件建模
2.1.1 资源约束
约束条件考虑:
1)每个火力单元最大执行任务能力
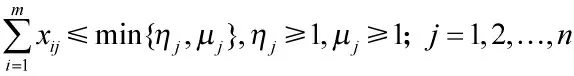
其中,ηj为火力单元j 的最大可用拦截弹数量,μj为火力单元j 当前可用导弹跟踪通道。
2)每个目标的最大被执行任务容量
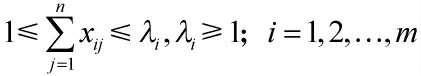
3)每个火力单元的工作状态
SZTj=0,表示火力单元j 的状态为正常,即可进行正常火力拦截。
2.1.2 空间关系约束

5)针对弹道导弹类目标,预测弹道与火力单元杀伤区有交点
设火力单元j 最大杀伤区对应的参数有:杀伤目标高度最大值Hmaxj、杀伤目标高度最小值Hminj、杀伤区远界斜距水平距离ryYj、杀伤区近界水平投影ryJj、最大航路捷径Pmaxj。
预测落点与火力单元的水平距离不大于ryYj且预测高度小于Hmaxj时有预测航路捷径小于Pmaxj,则认为该目标与火力单元杀伤区有交点。
6)针对弹道导弹类目标,预测弹道通过杀伤区时的速度不大于Vmaxj
可简化为:当预测高度小于Hmaxj时且预测航路捷径小于Pmaxj时,预测速度不大于Vmaxj。
2.1.3 其他约束
其他约束考虑人工干预的情况和火力单元反馈的建议放弃约束。其中,当指挥人员通过人工干预的方式或通过上级命令指定火力单元j 拦截目标i(或不拦截目标i)时,也需要增加约束条件:xij=1(或xij=0)。
另外,若火力单元反馈有对某目标的建议放弃标志SFQij,也应转换为如下约束条件:当SFQij=1 时,置xij=0,表示火力单元j 对目标i 给出放弃建议时,不将目标i 分配给火力单元j。
2.2 目标函数建模
定义目标函数为综合效能最大:
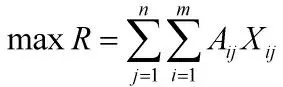
其中,Aij表示第j 个火力单元射击第i 个来袭目标的效益指标值。该值取决于火力单元j 对目标i 的射击效益值Cij、第j 个火力单元射击第i 个来袭目标时单次消耗费用Fij。
2.2.1 射击效益计算
火力单元j 对目标i 的射击效益值Cij由下式确定:

其中,Wi为第i 个来袭目标的威胁程度,取值为1/wi,wi为目标威胁排序。
取值方法如下:针对每个火力单元,首先按A类、B 类、C 类进行排序,然后同类目标中按可拦截时间Tyji从小到大进行排序。
A 类表示人工干预指定类目标;B 类表示对我方保卫要地有威胁的目标;C 类表示对我方无威胁的目标。

射击有利度Qij主要取决于火力单元j 对目标i的可拦截性fij、杀伤概率pij,以及目标在该火力单元发射区内停留时间T2ij(该参数可反映是否能多次拦截)、飞临发射区的时间T1ij(该参数可反映分配的紧急程度)。Qij表达式如下:

可拦截性fij通过空间约束条件可得,通过该方法将约束条件变为目标函数的一个因子。
火力单元j 对目标i 的杀伤概率pij与该目标是否被制导雷达跟踪上密切相关,未被制导雷达跟踪上的目标通常其信息来自于监视预警或上级情报,测量精度比较低,用该信息进行制导拦截,杀伤概率会极大降低;另外,传感器受干扰后,也会导致杀伤概率降低。因此,火力单元j 对目标i 的杀伤概率pij用下式进行修正:

当目标i 未指示给制导雷达时,影响因子k 与当前目标参数精度和火力单元制导体制有关,可取值为如下的值:

2.2.2 消耗费用指标计算
第j 个火力单元射击第i 个来袭目标时消耗的费用指标Fij计算公式如下:

2.2.3 综合目标函数建立根据第2.2.1 和第2.2.2 设计内容,火力任务规划的目标函数为:

从以上目标函数和约束条件可看出,火力任务规划的目标函数受到传感器分配和跟踪结果的影响,约束条件也受到人工干预的影响。因此,本文建立的模型是一个柔性可变的模型,根据战场状态的变化自动调整目标函数和约束条件。
3 基于离散粒子群的求解算法设计
针对第2 节中的任务规划模型进行求解,首先梳理满足SZTj=0 的火力单元,对满足上述条件的火力单元才进行目标分配;再考虑经人工干预目标,此类目标与火力单元的分配关系为固定值,不需再计算,即在求解模型过程中固定该值即可。因此,拦截器任务规划模型可简化为:
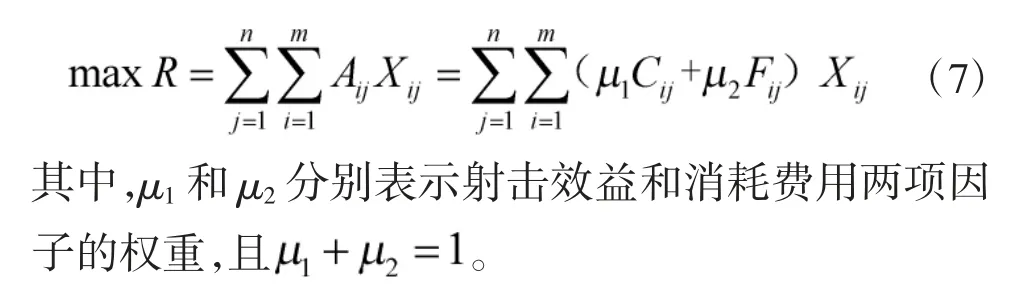
约束条件为:
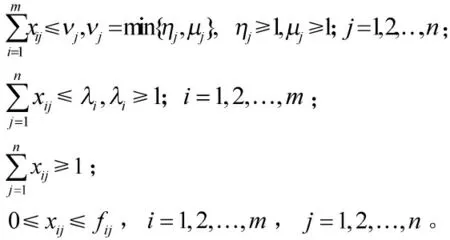
基于离散粒子群算法的求解步骤如下[8]:
第1 步:初始化粒子群,包括群体规模,每个粒子的速度和位置;
第2 步:计算每个粒子的适应度值,见式(8);
第3 步:对每个粒子,用它的适应度值和个体极值比较,如果个体适应度值大于个体极值,则将当前的个体极值替换为适应度值;用它的适应度值和全局极值比较,如果个体适应度值大于全局极值,则将当前的全局极值替换为个体适应度值;
第4 步:更新各粒子的位置和速度,见式(12)~式(13);
第5 步:当算法达到停止条件(前后两拍效能值误差小于一小数且持续20 拍,或达到最大循环次数),则停止搜索并输出结果;否则返回到第2 步继续搜索。具体流程如图1 所示。
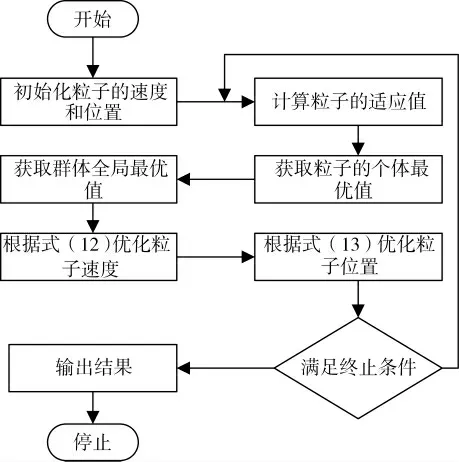
图1 基于离散粒子群优化算法实现流程
其中,粒子编码、适应度函数、位置和速度的更新方法设计如下:
1)粒子编码
粒子编码分为粒子的位置和速度两部分。每一个粒子都代表一个任务规划问题的可行解,因此,第k 个粒子的位置定义为n×m 的分配方案矩阵Xk。
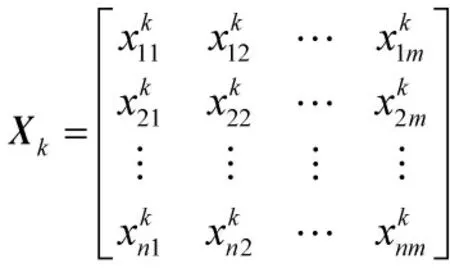
离散粒子群算法中粒子速度不再是连续空间所指的速度,而是用来计算粒子位置取值为1 的概率值,粒子k 的速度用矩阵表示如下:

2)适应度函数
适应度函数的取值方式通常考虑规划模型中的目标函数和约束条件,一般利用惩罚函数表示约束条件带来的影响,此时适应度函数可取如下公式:

由于m(·)函数是描述在资源有限的条件下种群增长规律的一个最佳数学模型,图像呈现S 形状,并且函数的输出值在[0,1]内,所以利用该函数将速度转换成目标与火力单元匹配的概率值。
4 仿真试验
4.1 试验环境
1)编程语言:Matlab;
2)试验平台:Windows XP;
3)CPU:3.3 GHz。
4.2 仿真参数选取及仿真结果

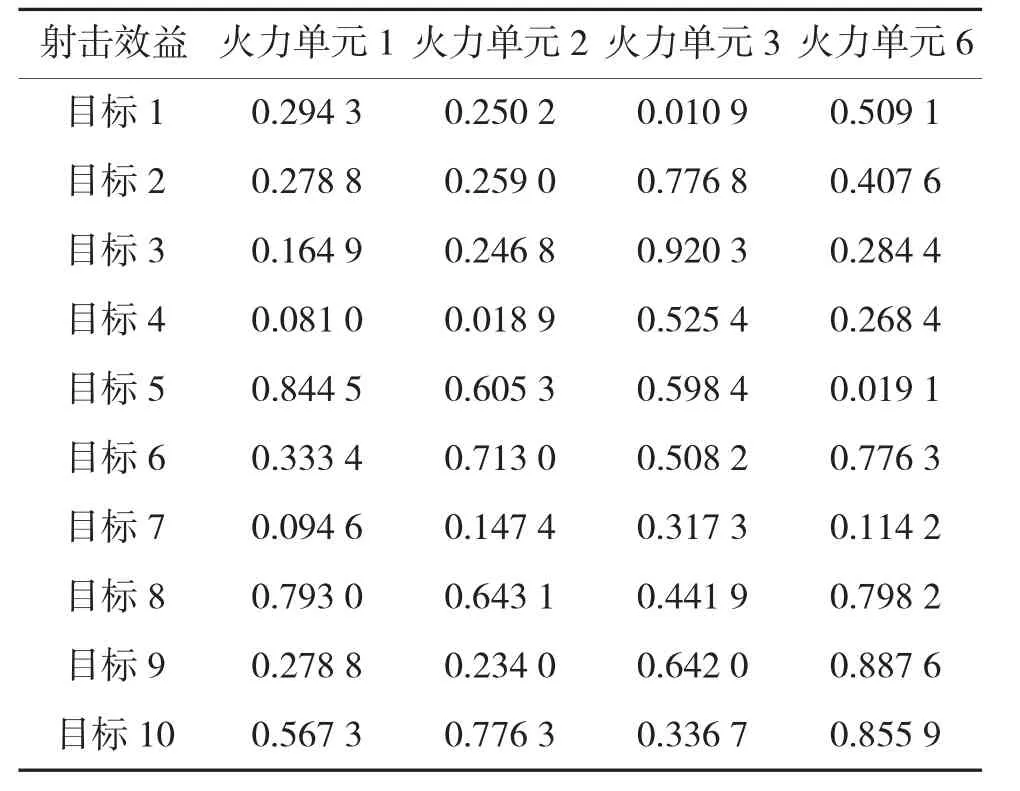
表1 火力单元对目标的射击效益(部分参数)
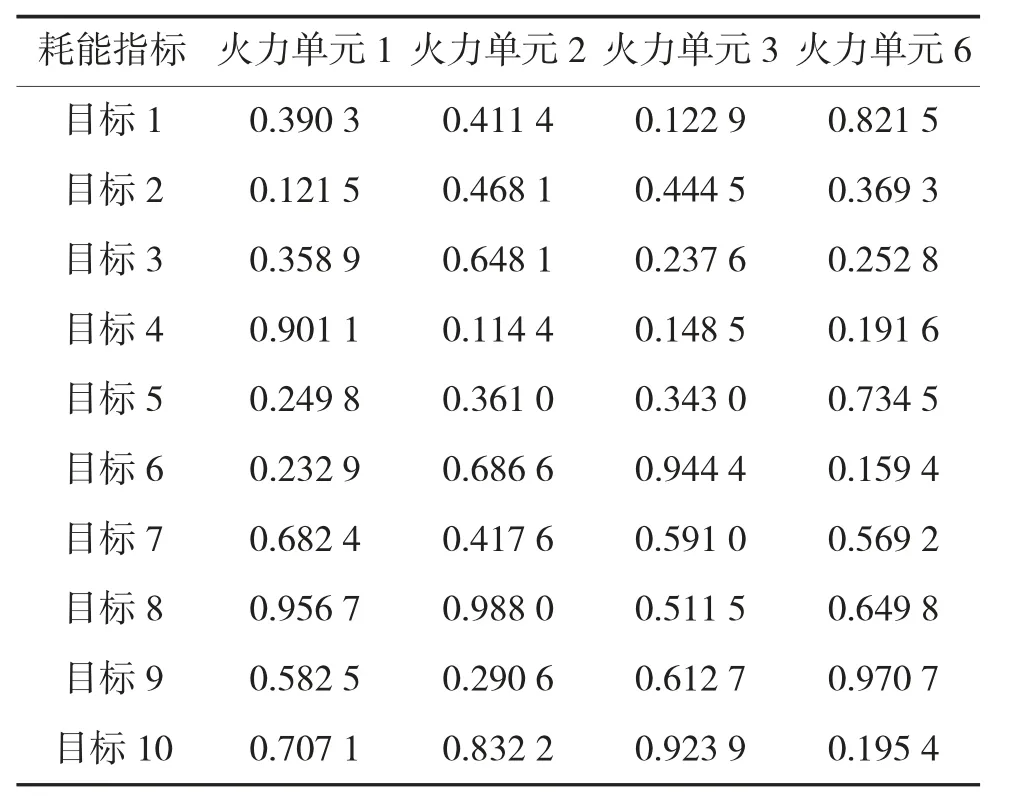
表2 火力单元对目标的消耗费用指标(部分参数)

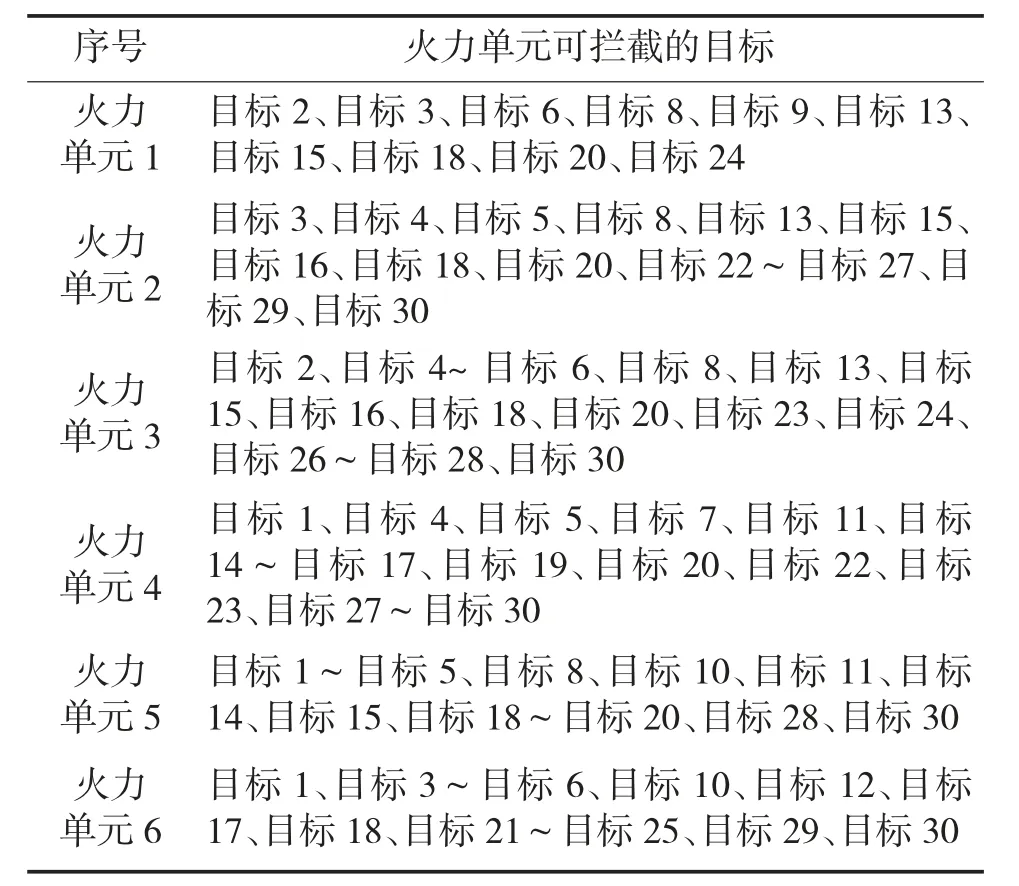
表3 火力单元对目标的可拦截性
对于初始种群个数选取,综合考虑寻优能力和消耗时间,一般来说种群规模越大寻优能力越强,但一次运行时间消费较大。考虑工程应用需求,采用多次仿真寻优的方法确定初始种群粒子个数。基本思想如下:
第1 步:确定初始粒子个数为N,例如:取值为5;
第2 步:基于上述初始参数进行问题求解,并记录运行时间和最终效能值;
第3 步:按一定规则改变初始种群粒子个数(如依次增加5),再次执行步骤2;当运行时间大于一定时间阈值(如:2 s)或者前后两次计算得到的最终效能值之差小于一小数(如后一次效能值的1 %)时,则退出。
经10 次仿真,取退出循环时粒子个数的平均值作为初始粒子种群个数。经仿真得出初始粒子个数为52。
利用上述初始参数,得到一次求解结果如图2所示。
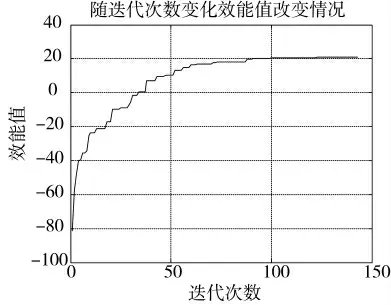
图2 随迭代次数变化粒子群优化效果
在上述条件下,得到目标与火力单元的配对关系如表4 所示。
从上述结果可得,优化计算得到的火力单元和目标的配对关系满足表3 中的可拦截性要求,且根据目标函数可知此结果效能值最大,因此,采用离散粒子群可对火力单元规划模型进行有效求解。
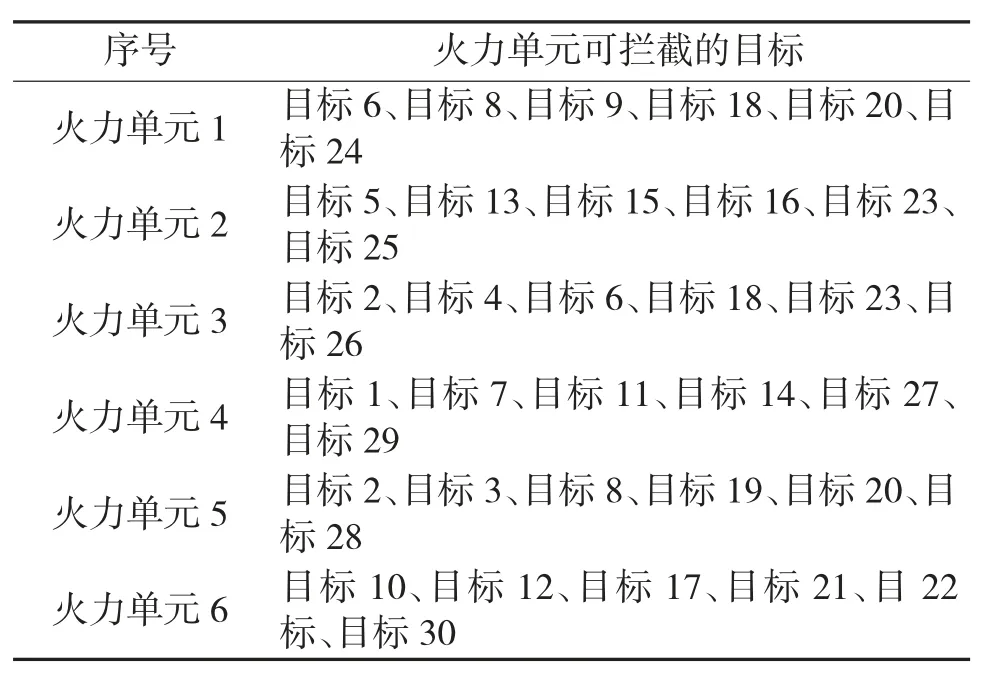
表4 火力单元与目标的分配关系
由于离散粒子群算法中粒子更新方法利用了随机变量,因此,每次执行结果不一样,在工程应用中为了保证目标分配的稳定性,可将上一拍得到的结果作为当前拍粒子初始值进行寻优处理。
5 结论
本文针对防空反导作战过程中的火力分配问题,结合作战实际详细设计了目标优化分配模型,并基于离散粒子群进行了模型求解方法设计和实例应用。该方法通过仿真验证了模型的合理性和算法的可行性,对区域反导指挥控制系统研制具有一定指导意义,具有良好的工程应用前景。
