基于VMD-LSTM的小电流接地系统故障选线方法
2021-02-01翟二杰舒征宇黄志鹏
翟二杰,舒征宇,汪 俊,黄志鹏
(三峡大学电气与新能源学院,湖北 宜昌 443000)
1 引言
我国中压配电网普遍采用小电流接地的方式运行,其发生单相接地故障的几率高达80%[1]。但由于发生单相接地故障时故障电流幅值较小,暂态过程持续时间短,容易受故障初始相角、接地电阻以及采样频率等因素影响,致使小电流接地系统故障选线问题成为配网自动化过程中的难题[2-4]。
近年来,以神经网络、支持向量机(Support Vector Machine,SVM)等为代表的基于人工智能的故障选线方法由于具有较高的选线精度和较好的鲁棒性,被广泛应用于配电网单相接地故障选线中。比如文献[5]根据故障初相角的不同,通过建立两类SVM分类器来解决接地电阻较大造成的配电网单相接地故障选线难的问题。文献[6]将蚁群算法优化后的BP神经网络应用于配电网故障选线,提高网络训练速度的同时,有效降低了选线误判率;文献[7,8]利用ADABOOST算法将多个分类方法级联,从而提高对复杂分类样本的处理能力,实现综合选线。上述各基于人工智能的方法在故障选线问题上取得了一定的成效,但都忽略了单相接地故障的零序电流是随时间变化的量,而BP神经网络和SVM分类器均属于浅层神经网络,它们与ADABOOST算法一样,在处理有延续性的时间序列方面存在不足,使得在某些极端情况下以及采样频率较低时容易造成误判。
长短期记忆神经网络(Long Short-Term Memory Neural Network,LSTM)作为一种具有记忆能力的递归型神经网络,其在处理有关时间序列的问题上具有显著优势,近年来在各个领域开始受到广泛关注。鉴于此,本文将LSTM神经网络应用于故障选线,提出一种基于VMD-LSTM 的小电流接地系统故障选线新方法。通过变分模态分解(Variational Mode Decomposition,VMD)算法将各出线零序电流分解成能直观体现零序电流基本组成的本征模态分量(IMF),将不同分量的能量值按时段代入到训练完成的LSTM网络中,实现故障选线。其实质是建立模态分量的能量随时序变化特征与故障线路之间的联系,从而实现不同场景下的故障线路快速辨识。
2 故障零序电流特性与组成
小电流接地系统可以分为中性点不接地系统和中性点经消弧线圈接地系统。本文以中性点经消弧线圈接地系统为例分析配电网系统发生单相接地故障后的零序电流特性及组成(中性点不接地系统可以看做是消弧线圈接地系统中电阻值无限大的一种特殊情况),假设C为消弧线圈接地系统的所有相对地电容,L0为等效电感,R0为零序回路中的等效电阻,rL、L分别为有功损耗电阻和电感,u0为等效零序电源电压。等效电路如图1所示。

图1 单相接地故障零序等效电路图Fig.1 Single-phase ground fault zero sequence equivalent circuit diagram
由图1可知,故障零序电流id由故障电容电流iC和流经消弧线圈的电感电流iL组成,其计算如式式(1)所示:
(1)
式中,ICm、ILm分别为电容电流和电感电流的极值;ω为系统角频率;ωf为暂态自由振荡分量的角频率;δ为自由振荡分量的衰减系数;φ为故障发生时刻的相角。
由式(1)可知,故障零序电流id由稳态分量和暂态分量构成,其中稳态分量为稳态电容电流和稳态电感电流的幅值之和,其变化频率与工频相近;暂态分量则由电容电流的暂态自由振荡分量与电感电流的暂态直流分量构成,前者振荡频率高,衰减快,后者几乎无振荡,衰减较慢甚至无衰减。由此可见,故障零序电流亦可看作是工频交流分量、高频振荡分量和衰减直流分量三部分叠加而成。
为此,本文采用VMD算法对各出线零序电流进行分解,提取高、中、低频分量,计算故障线路与非故障线路不同分量在不同时间段内的能量值,利用LSTM网络处理时间序列的显著优势实现故障选线。
3 基于VMD的零序电流分解
3.1 VMD分解原理及步骤
变分模态分解(VMD)是一种自适应、完全非递归的模态变分和信号处理的方法[9]。其基本原理是确定时间序列的模态分解个数后,可以自适应地匹配每种模态的最佳中心频率和估计带宽,有效分离本征模态分量(IMF)、划分信号频域,从而得到给定信号的有效分解成分,最终获得变分问题的最优解[10],有效弥补了EMD算法[11]分解不直观、模态混叠较严重的缺陷。VMD算法具体分解步骤如下:
(1)构造变分。其基本原则是寻求K个模态分量uk(t),在保证各个模态分量之和等于原始信号f的前提下,使模态分量估计带宽相加最小。对应的约束变分模型公式为:
(2)
式中,{uk}={u1,u2,…,uk}为各模态分量;{wk}={w1,w2,…,wk}为各模态分量中心频率;δ(t)为冲激函数。
(2)求解变分。为求得该约束变分问题的最优解,引入拉格朗日乘子λ(t)和二次惩罚因子α,将约束变分问题转变为非约束变分问题,得到增广拉格朗日表达式为:
(3)
式中,α可保证信号重构精度;λ(t)增强了约束的严格性。
经过上述变换,子模态的带宽估计问题就被巧妙地转变成寻求增广拉格朗日公式鞍点问题。采用乘法算子交替方向法(Alternate Direction Method of Multipliers,ADMM)结合傅里叶变换解决上述变分问题,通过式(4)~式(6)迭代优化ukn+1,wkn+1及λn+1,最终求得增广拉格朗日表达式的“鞍点”。
(4)

经过上述分析,VMD的主要迭代求解步骤可表示如下:
步骤1: 初始化{uk1},{wk1},λ1和最大迭代次数N,令n=0;
步骤2: 根据式(4)和式(5)更新uk,wk;
步骤3: 根据式(6)更新λ,n=n+1;
步骤4:根据式(7)分析收敛性(本文ε设定为1.0×10-6),若不满足式(7)或n (7) 由第2节分析可知,故障零序电流主要由工频交流分量、高频振荡分量和衰减直流分量组成。故本文设置VMD分解的分量个数K=3,从而将故障零序电流的三种分量进行有效分离。此处以第5.1节场景1为例来说明VMD分解的有效性,其故障线路零序电流VMD分解结果如图2所示。 图2 故障线路零序电流VMD分解结果图Fig.2 VMD decomposition results of fault line zero sequence current 从图2中不难看出,通过VMD分解后得到的三个本征模态分量与故障线路零序电流的三个组成分量特性一致,可以说明,经过VMD算法的3层分解后,直流分量、工频交流分量以及高频振荡分量被有效且直观地分离出来。 对比图2中的VMD分解结果可以发现,在相同时间段内三个模态分量的能量存在差异,且同一分量在不同的时间段内衰减速度也有所不同。 考虑到LSTM神经网络处理时间序列的显著优势,本文将采集到的零序电流信号进行VMD分解后,分别计算不同时段下各个分量的能量值,将其代入到LSTM网络中进行故障选线。能量计算步骤如下: 步骤1:将零序电流信号平均划分为M个时间段,记为[T1,T2,…,Ti,…,TM],其中,i为时间段编号。由于单相接地故障暂态过程持续时间较短,常在1~3个工频周期内结束[12],故本文选取故障发生后的2个工频周波进行时段划分。本文M取8,此时网络训练时间最短,准确率也较高。 步骤2:VMD分解的第k个分量IMFk在Ti时间段的能量Ek,ij为: (8) 式中,j为线路编号;Ti,max和Ti,min分别对应Ti时间段的时间上限和时间下限;K为零序电流VMD分量个数,本文K取3。 在实际场景中,当出现故障初始相角较小、接地电阻较大、采样频率较低等极端情况时,采集到的各出线零序电流幅值较小,使得VMD分解后的各分量幅值和能量值也较小。为增强VMD分解后的各分量信号,本文对故障发生后的所有零序电流进行VMD分解,得到各线路的高、中、低频模态分量后,根据式(9)对其进行归一化处理,再进行能量计算。 (9) 式中,IMFkg,j表示第k个模态分量的归一化幅值;IMFk,j表示第k个模态分量的实际幅值;IMFkmax,j表示第k个模态分量中的幅值最大值。表1所示为5.1节场景1中各线路零序电流VMD分量归一化前能量值Ek,j和归一化后能量值Ekg,j的对比结果。 由表1可知,归一化处理后,各健康线路零序电流VMD分量能量值相较于故障线路的同一分量能量值均有不同程度的增大,相当于变相增强了各线路的零序电流幅值。 表1 归一化前后各线路零序电流VMD分量的能量值Tab.1 Energy value of VMD component of zero-sequence current of each line before and after normalization LSTM(长短期记忆神经网络)是一种具有长短时记忆功能的深度神经网络,可以很好地处理时间序列数据的预测和分类问题,目前已广泛应用于语音识别、自然语言处理等领域中[13-15]。 图3所示为LSTM的结构图,其主要由三个门(即图3中的虚线框图,从左往右依次为遗忘门、输入门、输出门)组成,通过三个门的相互配合,LSTM能更加有效地决定哪些历史信息被遗忘,哪些输入信息被保留,哪些信息可以被输出,从而更加高效地处理时间序列。 图3 LSTM结构图Fig.3 LSTM structure diagram 图3中,x(ti)为LSTM神经网络ti时刻的网络输入,本文中x(ti)=[E1,ij,E2,ij,E3,ij];h(ti)为ti时刻的网络输出;C(ti)为ti时刻网络的单元状态输出;f(ti),i(ti),o(ti),C′(ti)分别表示遗忘门输出,输入门输出,输出门输出和当前输入单元状态;σ和tanh均为激活函数,其中σ为sigmoid函数,tanh为双曲正切函数。 在LSTM模型训练过程中,首先根据初始设定的参数按照式(10)运算更新LSTM模型中各门参数,并进一步根据式(11)运算得到网络的输出结果: (10) (11) 式中,Wf、Wi、Wc、Wo分别代表遗忘门、输入门、当前输入单元状态和输出门的权重矩阵;bf、bi、bc、bo则表示遗忘门、输入门、当前输入单元状态和输出门的偏置矩阵;此8个参数矩阵为待求的参数矩阵,在模型的训练过程中逐步优化和更新。 按照式(11)计算出网络的输出值后,根据式(12)计算输出值与实际值之间的误差C,将误差反向传播,并按式(13)更新网络权重和偏置: C=|h′(ti)-h(ti)| (12) (13) 式中,h′(ti)表示LSTM网络实际值,本文取值0或1,其中0代表健康线路,1代表故障线路;h(ti)表示LSTM网络输出值;α表示学习率;W和b代表更新前的权重和偏置;W′和b′代表更新后的权重和偏置。 由前文分析可知,故障零序电流的直流分量、工频交流分量以及高频振荡分量可以通过VMD算法 有效且直观地分离出来。不同的VMD分量在同一时间段内的能量大小不同,且各分量在不同时间段的能量值(即能量衰减速度)也有差异,其中,高频振荡分量衰减最快,直流分量衰减较为缓慢,工频交流分量几乎不衰减。 图4 基于VMD-LSTM的故障选线流程图Fig.4 Flow chart of fault line selection based on VMD-LSTM 为此,本文借助LSTM网络处理时间序列的显著优势,依据故障线路与非故障线路零序电流各分量能量随时间变化特征的不同实现故障选线。 基于VMD-LSTM的小电流接地系统单相接地故障选线流程图如图4所示,步骤如下: 步骤1:采集各线路零序电流Ij。其中j为线路编号。 步骤2:VMD分解。确定预分解分量的个数K,根据式(2)~式(7)对Ij进行VMD分解,构建并求解变分。本文设置K=3,得到第j条线路零序电流的三个模态分量[IMF1,j,IMF2,j,IMF3,j]。 步骤3:归一化处理。根据式(9)将IMFk,j进行归一化处理,所得分量记为IMFkg,j。 步骤4:时段划分。将采集到的零序电流数据序列按采集时间划分为M个时段[T1,T2,…,TM]。根据式(8)计算IMFkg,j在Ti时段下的能量值Ekg,ij,其中i表示时间段编号,M取8。 步骤5:将各分量能量值Ekg,ij按时段输入到LSTM神经网络,训练LSTM 神经网络,建立不同分量的能量值随时间变化特征与故障线路的多层级映射关系,实现故障选线。 本文以10 kV中性点经消弧线圈接地系统为研究对象,利用MATLAB/Simulink软件搭建仿真模型,如图5所示。 图5 中性点经消弧线圈接地系统示意图Fig.5 Schematic diagram of neutral point grounding system through arc suppression coil 图5中共包含五条出线,其中“J”表示架空线路,“D”表示电缆线路。消弧线圈采用5%的过补偿方式,其余线路参数如表2所示。假设0.02 s时系统发生单相接地故障,持续时间为0.08 s,选择算法为0de23tb,relative tolerance为1e-3,其他参数为默认值。 表2 各线路电气参数Tab.2 Electrical parameters of each line 如表3所示,本文通过改变仿真模型中的故障初始相角、故障点接地电阻、故障点距母线距离来模拟不同场景下的系统单相接地故障,并使用“To Workspace”模块对仿真波形进行采样,采样频率为400次/周波。 表3 典型接地故障的样本集合Tab.3 Sample collection of typical ground faults 表3中,φ为故障初始相角,Rf为故障点的接地电阻,df为故障点到母线的距离。实验共采集到750组非故障样本,150组故障样本,总计900组样本。将故障样本与非故障样本进行混合后,随机选择800组样本来进行VMD-LSTM模型的训练,剩余100组作为测试样本来检验故障选线的准确率,其中LSTM网络输出值接近于1的判断为故障线路,接近于0的判断为非故障线路。 表4所示为测试样本中三种典型的单相接地故障,本文将以此来说明所提方法的有效性。 表4 三种典型的故障场景Tab.4 Three typical failure scenarios 图6为三种场景下故障线路零序电流对比。 图6 场景1至场景3故障线路零序电流对比Fig.6 Comparison of zero-sequence currents of fault lines in scenarios 1 to 3 由图6可知,发生单相接地故障后,故障线路零序电流的幅值会受到故障初始相角、接地电阻以及故障距离的影响而呈现出明显的差异。为此本文分别将三种场景下采集到的各出线零序电流进行VMD分解和分量归一化处理,按时间段计算各分量能量值。图7所示即为各线路VMD分量能量随时间变化曲线。 从图7中可以看出,在上述三种场景中,故障线路与非故障线路的VMD分量能量值随时间变化曲线存在明显的差别,故利用可以处理时间序列的LSTM神经网络来进行故障选线具有很大的优势。鉴于此,本文将各分量的能量值按时段依次输入到训练完成的LSTM神经网络中,所得选线结果如表5所示。 表5 VMD-LSTM故障选线结果Tab.5 VMD-LSTM fault line selection results 由表5可知,基于VMD-LSTM的故障选线方法可以取得良好的选线效果。此外,对100组测试样本利用VMD-LSTM方法进行故障选线,选线准确率高达94.63%。 近年来,大量的电力电子设备被广泛应用于电力系统中,这些装置会产生大量的噪声数据,并严重影响故障线路与健康线路的零序电流分布,增加选线难度。为此,本文通过在采集到的各线路零序电流波形上叠加信噪比为10 dB的高斯白噪声来检验噪声干扰情况下VMD-LSTM选线方法的有效性。 图7 各场景VMD分量能量随时间变化图Fig.7 Variation of energy of VMD components of each scene with time 图8所示即为上述3个场景添加高斯白噪声后的故障线路零序电流。 图8 噪声信号对零序电流信号的影响Fig.8 Effect of noise signal on zero-sequence current signal 从图8中不难看出,添加高斯白噪声后,场景1和场景2故障线路零序电流受噪声影响较小,而场景3故障线路零序电流变化较为明显。受篇幅所限,以下将主要以场景3为例来说明噪声干扰情况下VMD-LSTM方法的选线效果。噪声干扰时场景3中的VMD分量能量随时间变化曲线如图9所示。 图9 噪声干扰时场景3VMD分量能量随时间变化曲线Fig.9 Variation curve of energy of VMD component of scene 3 with time under noise interference 如图9所示,加入噪声干扰后,故障线路与非故障线路的VMD分量能量值随时间变化曲线依然存在差别,将各VMD分量能量按时段依次输入到LSTM神经网络后依然可以实现正确选线。此外,本文将添加高斯白噪声后的100组测试样本,分别采用VMD-LSTM选线法、文献[5]中的SVM分类器(EEMD-SVM)、文献[6]中的蚁群算法优化后的BP神经网络(BP)以及文献[7]中的ADABOOST算法进行对比,所得结果如表6所示。 表6 噪声干扰下的故障选线结果Tab.6 Results of fault line selection under noise interference 由表6可知,在有噪声干扰的情况下,经过蚁群算法优化后的BP神经网络选线准确率较低,这是因为当出现类似于场景3的高阻接地故障时,其本身故障特征较弱,且BP神经网络结构简单,抗干扰能力差,因而在加入高斯白噪声后其选线误判率较高。 工程应用中,各信号采样不同步的问题往往难以避免。为此,本文在100组测试样本中将故障线路的采样滞后健康线路0.002 s,如图10所示。 图10 采样不同步时的各线路零序电流信号Fig.10 Zero sequence current signal of each line with unsynchronized sampling 图11所示为采样不同步时场景3中各线路VMD分量能量随时间变化曲线。 图11 采样不同步场景3 VMD分量能量随时间变化图Fig.11 Variation of energy of VMD components in scene 3 with time with unsynchronized sampling 对比图7和图11中场景3的VMD分量能量值随时间变化曲线,可以发现,采样不同步时,故障线路的VMD分量能量峰值出现了后移。在100组测试样本中采用前文所述的4种方法进行对比,所得结果如表7所示。 表7 采样不同步时的故障选线结果Tab.7 Fault line selection results with unsynchronized sampling 由表7可知,当发生采样不同步时,相比于本文所提的VMD-LSTM方法,其余方法选线准确率均有所下降。这是因为发生采样不同步时,各线路零序电流发生时序错位,使得故障线路与健康线路同一时刻的极性、幅值差异规律被打乱,依靠一个或多个时间点对应的线路幅值和极性差异来进行故障选线的方法误判率较高。而本文通过计算多个连续时间段的能量,尽量减小点错位带来的选线误差,又借助LSTM神经网络的“记忆”特性,基于较长时间尺度的能量变化曲线来实现故障选线,因而受采样不同步的影响较小。 实际采样的零序电流信号由于采样频率的限制,有些故障信息可能丢失,致使故障线路的特征不明显,造成“误选”或“漏选”[16,17]。为验证本文所提方法在采样频率较低时的有效性,本文以5.1节场景1为基础,将故障线路替换为线路4,分别以每个周波10、40、100、400次的频率对故障线路零序电流进行采样,所得图形如图12所示。 图12 不同采样频率对零序电流信号的影响Fig.12 Effect of different sampling frequencies on zero-sequence current signal 由图12可知,当以每个周波10次、40次的频率进行采样时,其零序电流在故障初期幅值较小,存在较大的能量损失,影响故障选线的准确率。 考虑到实际工程应用的技术限制,本文在上述场景的基础上,以40次/周波的频率对线路4零序电流信号进行采样,并在此基础上进行故障选线,图13所示为低频采样时各线路VMD分量能量随时间变化曲线。 如图13所示,低频采样情况下,各线路的VMD分量能量值随时间变化曲线相较于其他故障类型变化较为明显,但故障线路与健康线路差别仍较大。在100组测试样本中采用前文所述的4种方法进行对比,所得结果如表8所示。 由表8可知,当采样频率较低时,采样得到的零序电流信号会产生能量损失。此外,当暂态过程持续时间较短,而采样频率较低时,采集到的零序电流信号相较于原始信号会丢失一个或多个波峰、波谷信息,依靠极性、幅值、初始相角进行故障选线的EEMD-SVM、BP、ADABOOST等方法发生选线错误。而本文所提方法在VMD分解后采用归一化处理,变相地对VMD分量信号进行了增强,且本文基于长时间尺度的能量变化规律进行故障选线,因此,即便在采样频率较低、信号存在能量损失的情况下,依然可以保障故障选线结果的准确率。 图13 低频采样时VMD分量能量随时间变化图Fig.13 Time-dependent graph of VMD component energy of scene 1 during low-frequency sampling 表8 低频率采样时的故障选线结果Tab.8 Fault line selection results at low frequency sampling 本文提出一种基于VMD-LSTM的小电流接地系统单相接地故障选线方法。本文首先对系统中各线路的零序电流进行VMD分解和归一化处理,进而得到不同频段零序电流的增强分量;考虑到长短时记忆神经网络在处理时间序列方面的显著优势,本文将增强后的各零序电流分量进行时段划分,并计算各时段能量,将其作为神经网络的输入,进而实现故障选线。仿真结果表明,本文所提方法在有噪声干扰、异步采样、低采样频率、接地电阻较大等故障特征较弱的场景下具有较高的选线准确率。3.2 基于VMD分解的能量计算



4 基于VMD-LSTM的故障选线
4.1 LSTM算法简介

4.2 基于VMD-LSTM的故障选线流程

5 仿真案例分析


5.1 基于VMD-LSTM故障选线结果分析




5.2 噪声干扰对方法选线结果准确率的影响




5.3 异步采样对方法选线结果准确率的影响



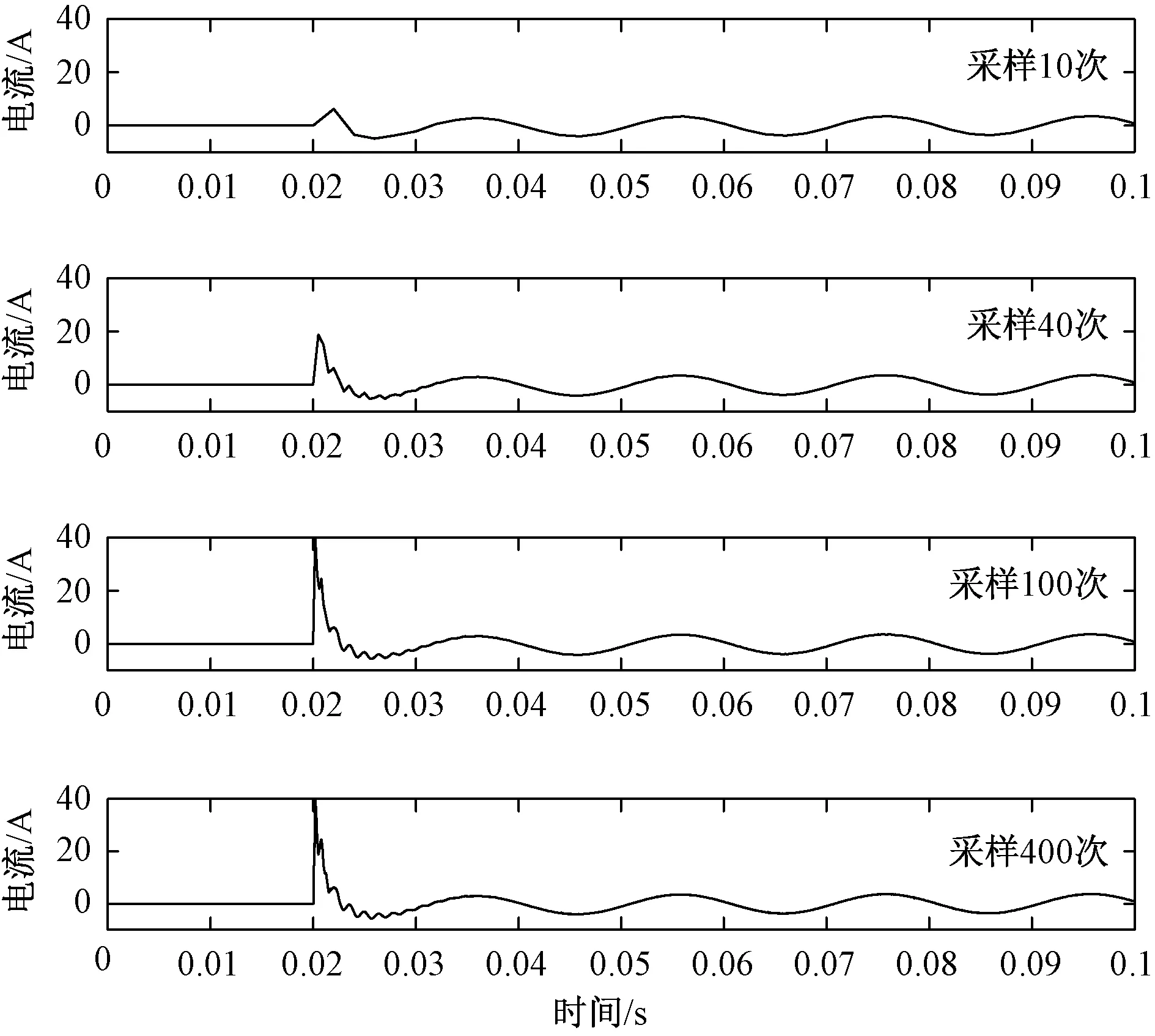
5.4 采样频率对方法选线结果准确率的影响


6 结论
