基于SE-DenseNet的变压器故障诊断

郭如雁，彭敏放，曹振其

(湖南大学电气与信息工程学院，湖南 长沙 410082)

1 引言

变压器是电力系统中传输电能的重要设备，关于变压器故障诊断的研究对电力系统的运行、维护和检修具有十分重要的意义。在电力系统中500/220 kV和500/330 kV油浸式变压器是各变电站常用的设备，虽然变压器的故障率较低，但由于附件(如分接开关)质量问题，线匝、线饼间的绝缘损坏，内部绝缘距离不够，绝缘油被污染，雷击，出口短路，长期过载，过电压运行等内外部原因，均能造成变压器的重大故障，给国民经济造成严重损失。为保障电力系统的安全可靠稳定运行，国内外各学者围绕变压器故障诊断，做了多个方向的研究。文献[1]通过小波变换对绕组行波的频率响应进行分析，文献[2]通过测量变压器原边电压电流利用二端口网络知识在线监测短路阻抗，文献[3]通过提取变压器振动信号的时域特征进行主分量分析，文献[4]通过迁移学习将故障数据清洗得到的有效知识输入支持向量机进行故障分类，文献[5]基于变压器油溶解气体(Dissolved Gas Analysis, DGA)的油色谱数据结合深度神经网络进行分析等。由于前四者分别具有电磁干扰、对故障反映的灵敏度低、感应高压造成的安全隐患、集成多个二分类诊断器效率不高等问题，目前基于DGA的故障诊断[6,7]依然是变压器故障诊断的主要方法之一。

基于DGA诊断有实时在线进行，安全无干扰、发现变压器早期潜伏性故障[8]等优点，结合深度学习神经网络强大的特征提取并进行多分类的能力，能较大地提高变压器故障诊断的准确率，并且所建模型具有性能稳定、易收敛的优点，是一个新颖且发展前景广阔的研究方向。至今国内已知的基于深度学习的变压器故障诊断神经网络有四种[9-12]。这四种网络均能实现多分类，但由于变压器故障样本数据较少，需要使用数据增强进一步提高模型的泛化能力。卷积神经网络擅长提取抽象特征，能够将高维空间向量非线性变换映射到低维空间从而实现线性可分，在图像分类、目标检测等问题上取得了很大的成功。本文所提出的基于SE-DenseNet变压器故障诊断模型,就是深度压缩、激励网络和深度稠密网络的结合。模型的输入采用无编码比值法[13]所提出的9种不同组合形式的特征气体比率值，模型的输出为9种故障类型的各自概率值，将概率值代入softmax交叉熵损失函数中，再使用Adam算法最优化该损失函数，最终使SE-DenseNet模型的预测准确率收敛。

基于大云物移智技术平台的智能传感器在线监测的变压器油色谱数据不平衡，且故障数据量少，为此提出WGAN[14]网络进行数据增强，即样本生成技术，WGAN可生成同一故障类别同特征的多类样本数据，为样本原始特征非线性化表示提供了充足的数据源。本文在已有故障数据的基础上利用WGAN 将故障样本数量增加近一倍。实验证明SE-DenseNet模型预测效果在同类网络中最好。

2 SE-DenseNet框架

2.1 SE module介绍

本文构造一种能学习到特征图各通道的空间相关性和各通道的权重大小的SE模块，在DenseNet神经网络中加入SE[15]操作。SE模块对输入其中的特征图每个通道的重要性进行学习，将得到的权重与对应的通道相乘，输出各通道权重得到校准后的特征图，即进行特征选择，使有用特征得到加强，无用特征得到削弱，完成特征重标定，以提高神经网络的辨别能力，其功能模块如图1所示。

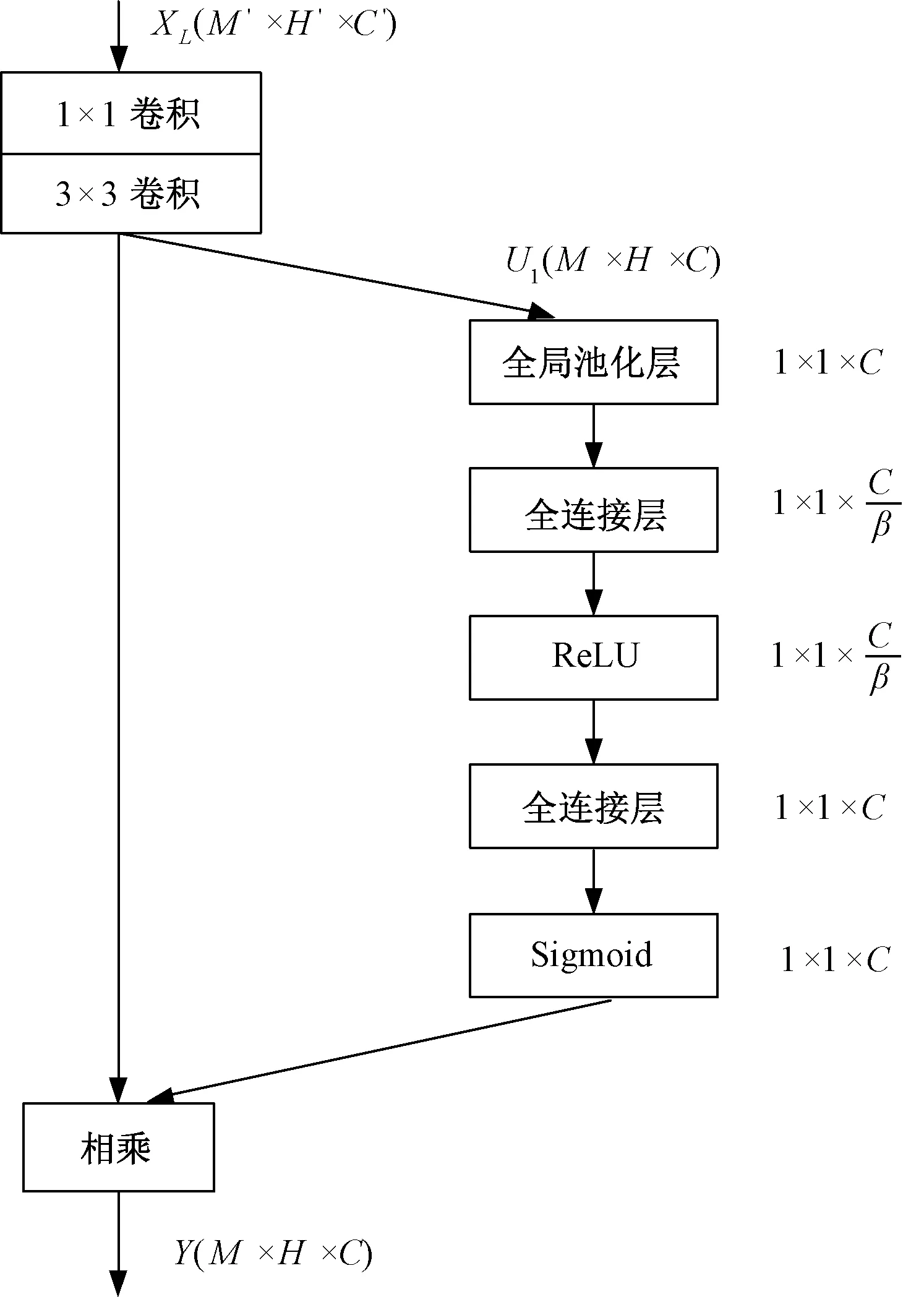
图1 SE模块图Fig.1 SE module

(1)通过卷积操作将第L层特征图XL变换为张量U1，即：

U1=WL⊗f(BN(WL-1⊗f(BN([X0X1…XL-1]))))

(1)

式中，BN表示批量归一化处理；f(·)为ReLU函数；WL-1，WL分别为大小为1×1，3×3 的卷积核。

(2)挤压操作，此环节是全局池化层，将特征图形状[M,H,C]压缩为[1,1,C]，得到该层特征图的c个通道的数值分布情况，其数学描述如式(2)：

(2)

式中，uc表示卷积操作后第c个通道特征图；zc为挤压操作后第c个通道特征图。M,H,C代表特征矩阵U1的三维信息；c为第个c通道。

(3)激励操作，其数学原理是式(3)：

sc=Fex(z,W)=σ(g(z,W))=σ(W2f(W1zc))

(3)

式中，W1∈R(C/β)×C；W2∈RC×(C/β)；f(·)表示ReLU激活函数；σ是Sigmoid函数；β为维度变换率，在本文中取16，以减少计算量。最后将所得尺度矩阵sc的c个元素与特征图U1的c个通道一一对应相乘，输出得到Y=[y1y2…yc]，其数学原理是式(4)：

Y=Fscale(uc,sc)=sc·uc

(4)

式中，sc表示先挤压后激励所得到的向量，其维数为c；uc表示卷积操作后的特征图，其通道数为c。

由以上分析可知，SE模块通过先压缩再激励输入，将特征图以通道为单位映射成一个具有全局性的实数，最后将此实数与输入对应相乘，完成特征图各通道的相关性学习。

2.2 SE-DenseNet网络结构特点

DenseNet[16]主要特点是将每一层特征图与前面所有层的特征图在通道数的维度上进行累加，网络的每一层对特征值进行少量的学习，降低了冗余性[17]。Densenet的优点是通过稠密连接将神经网络的各层特征进行了融合，特征得到了重复利用，可以减少计算量，其跳跃结构使各层输入特征图可以直接与最后的损失函数相连，接受最终损失函数的监督，解决梯度消失问题，使网络的信息流通顺畅。

本文介绍的SE-DenseNet将SE模块与Densenet的优点结合，其网络配置信息如表1所示，结构如图2所示。由表1和图2可知，相较于传统DenseNet神经网络，SE-DenseNet的创新之处在于：

(1)将稠密连接结构块上的转换层中包含的平均池化层去掉，保留BN层，ReLU层和1×1的卷积，得到新的转换层，可以保留全局信息，增强网络的稳定性，减少资源占用。

(2)SE模块再将经稠密连接块得到的特征图与经新的转换层得到的特征图进行各通道权重校准，增强有益特征，抑制无用特征，使网络的性能得到有效提高。

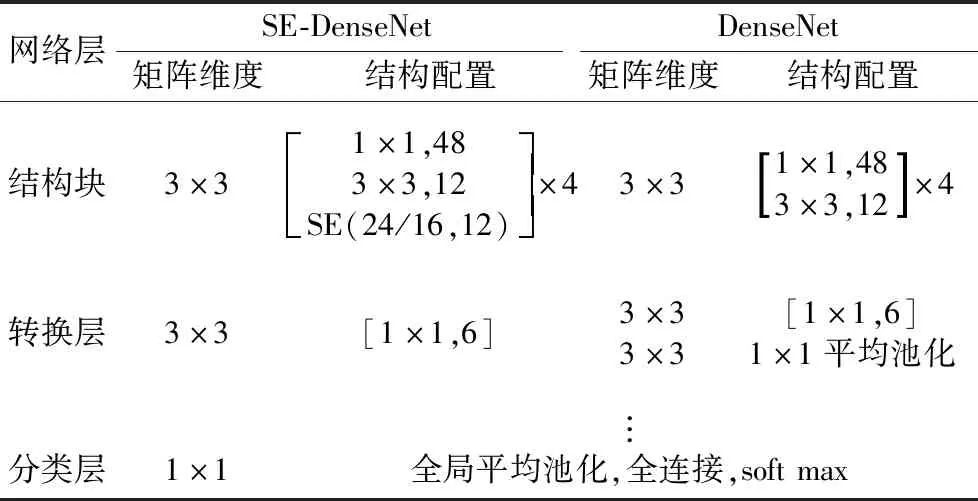
表1 SE-DenseNet网络配置信息表Tab.1 SE-DenseNet network configuration information

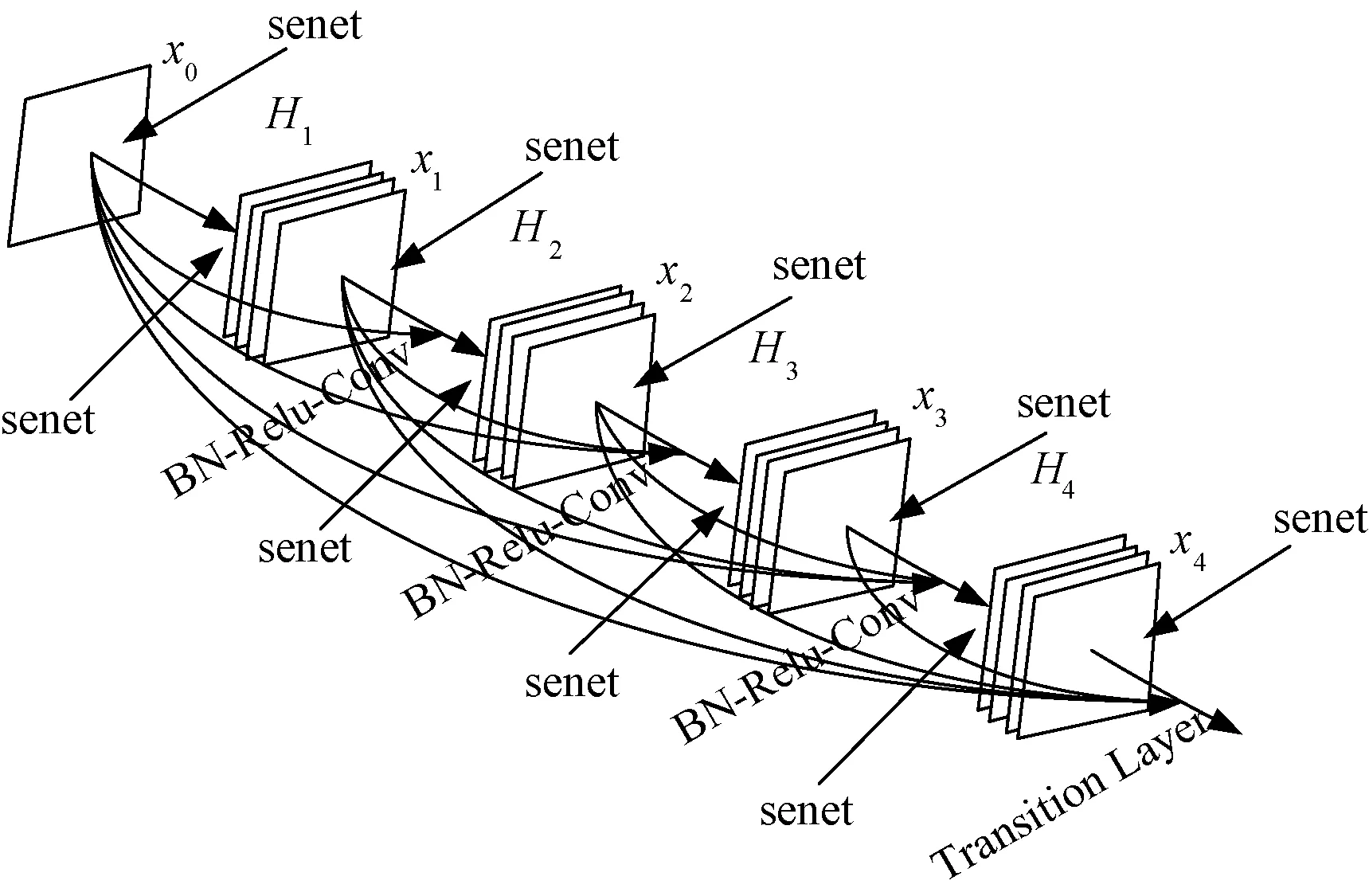
图2 SE-DenseNet示意图Fig.2 SE-DenseNet

3 提高模型性能的方法

本文在DenseNet程序的基础上，采用6种方法改进SE-DenseNet模型的收敛效果和预测准确率：指数衰减学习率确保模型参数较快的更新速度和在全局最优点收敛；L2正则化使模型待估参数衰减，以减少计算资源占用；dropout减弱特征之间的依赖性，以防止过拟合；Adam算法使用迭代次数和指数衰减率对梯度均值和梯度平方均值进行了校正，使算法对梯度的预测更加精准；使用批量归一化可减少初始化的影响，提高训练速度；运用ReLU函数可提高神经网络逼近任意非线性函数的能力。这6种方法具体介绍如下。

3.1 指数衰减学习率

学习率是用梯度更新模型待估参数的速率，当学习率较大时，网络参数更新较快，在模型训练初期局部收敛较快，随着迭代次数增加时，模型会在全局最优点回荡，此时较小的学习率能使模型收敛，因此提出学习率随迭代次数进行指数级衰减，如式 (5)：

decayed_learning_rate=learning_rate×decay_rate^(global_step/decay_steps)

(5)

式中，decayed_learning_rate为衰减后的学习率；decay_rate是衰减指数；global_step是当前的迭代轮数；decay_steps是衰减速度。

3.2 Dropout策略

Dropout是一种正则化方法，它在一次训练中让隐含层神经元以概率P抑制，丢弃隐含层一部分神经元，同时保留被丢弃节点的参数值，在误差反向传播时仅更新被激活神经元的参数值，在下一次训练时重复上述过程，每次训练得到一个不同的神经网络，最后集成这些网络。在测试集上运行模型时，将模型学习到的权值矩阵乘以概率P，使模型预测准确。dropout将性质相反的过拟合相互削弱，在不同隐含层子集中均可学到相应特征，以减弱特征之间的依赖性，防止过拟合。

3.3 L2正则化

为了将权重和偏置参数收敛为稀疏性更好的矩阵，以减少计算量，通常在目标函数上附加一项参数惩罚项，在用梯度下降更新参数时，权重矩阵会乘以一个小于1的缩放因子，将权重正则化至零点，若未添加惩罚项的原损失函数的Hessian矩阵为H，则H的特征值越小，权重收缩至零点的效果越明显，L2正则化公式为：

(6)

式中，ω，b为神经网络模型待寻优参数θ；X为输入向量；ypredictedi为预测值；yi为真实标签值；α为正则项系数。α能增加输入X的方差，因此L2正则化使权重往稀疏性好的方向衰减，在以下要介绍的Adam算法中，f(θ;X,y)为损失函数。

3.4 Adam算法

Adam算法是一种用一阶梯度对损失函数进行最优化的方法，该算法所需存储小，准确率高，能避免模型在最优点大幅振荡，因此适用于大规模数据集和参数的神经网络。该算法的流程如图3所示。

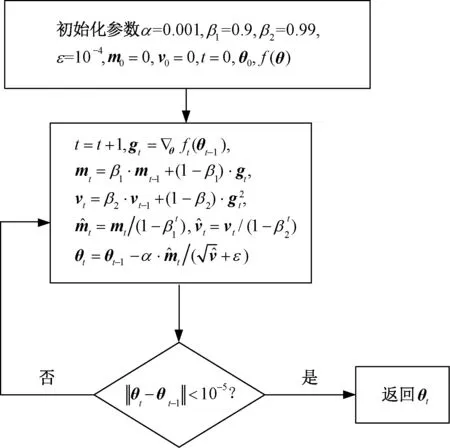
图3 Adam算法流程Fig.3 Adam algorithm flow

(1)设置超参数学习率α，一阶矩估计指数衰减率β1，二阶原点矩估计指数衰减率β2，α采用指数衰减学习率，其值从0.001开始随迭代次数t按指数规律衰减。初始化参数θ0向量的各元素，一阶矩向量m0，二阶矩向量v0。

(2)求出f(θ)对θ的偏导数θf(θt-1)，得梯度向量gt，用gt按指数加权平均值公式更新带偏差的一阶矩估计mt，同理，用梯度向量的逐元素平方更新带偏差的二阶原点矩估计vt。用指数衰减率β1，β2计算偏差修正的一阶矩估计和二阶原点矩估计将与的比值取代梯度下降法的gt，对参数进行更新，图3中“·”表示乘法。

(3)进行收敛准则校验，若收敛则停止更新返回参数θt，否则重新计算步骤(2)、(3)直至收敛。

3.5 批量归一化

对批量归一化(Batch Normalization，BN)做出解释：训练网络时，对于正向传播，一个批量的每张特征图输入神经元为x={x1,x2,…,xm}，归一化公式为：

(7)

式中，u为样本均值；σ2为样本方差；缩放系数γ和平移系数β为类似于权重的可学习参数。通过变换重构，使网络学习到所要提取的特征的数据分布，反向传播时通过链式求导求得梯度，从而改变训练权值；测试网络时，对于多个批量样本的均值u和方差σ2，计算u′,σ′时采用滑动平均的技巧：

(8)

式中，变量u′在第t批次记为u′(t)；θ(t)为变量u′在第t批次取值；α∈[0,1)，当α=0时，则不使用滑动平均；当α≠0，使用滑动平均计算法，减少内存占用。通过BN可以防止梯度弥散和爆炸。

3.6 ReLU激活函数

使用ReLU非线性激活函数可以使神经网络拟合各种函数，ReLU函数的定义是：

f(x)=max(0,x)，x∈(-∞,+∞)

(9)

式中，x为输入张量。该函数可将输入映射到正数域，ReLU函数占用计算资源小，当输入为负数，该神经元处于抑制状态，当输入x为正值时，由于其导数为常数1，不会导致梯度变小，模型参数能保持收敛。综上可得基于SE-DenseNet变压器故障诊断流程如图4所示。

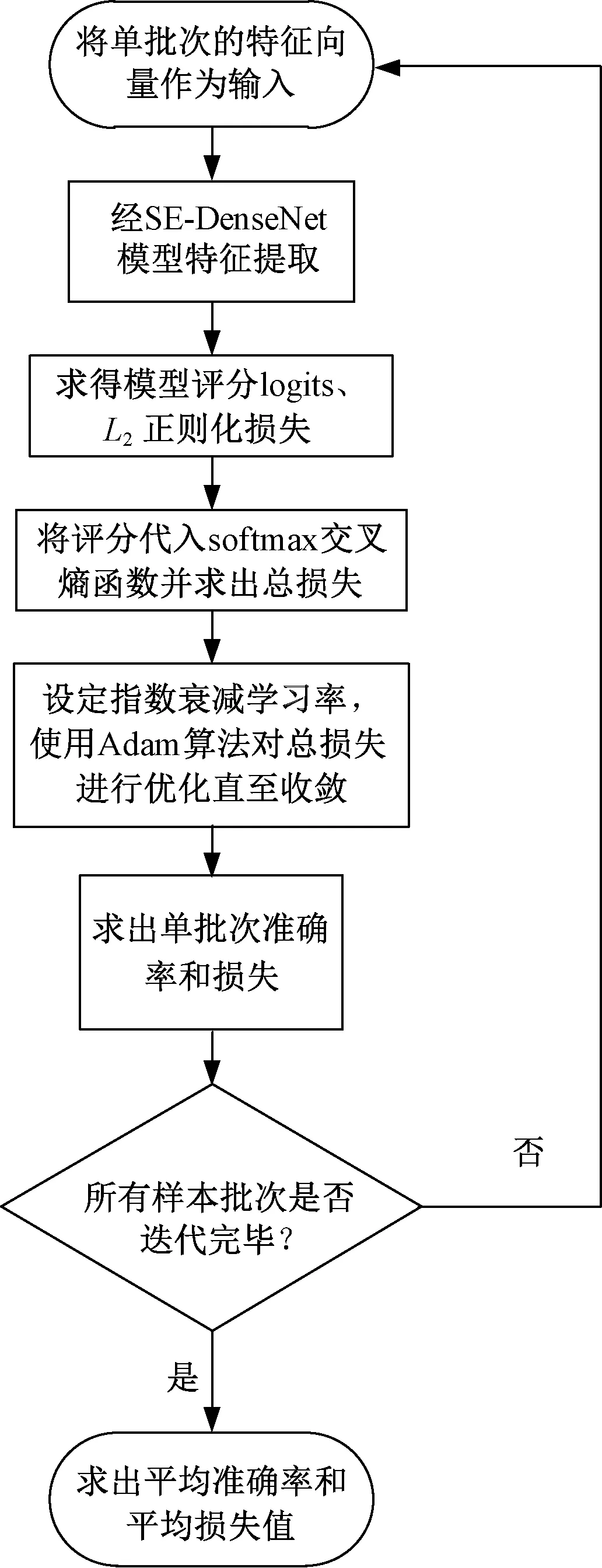
图4 SE-DenseNet诊断流程Fig.4 SE-DenseNet diagnosis process

4 特征向量选取

4.1 无编码比值法及输入特征向量的选取

根据《变压器油中溶解气体分析和判断导则》[18]所述，变压器发生故障时，变压器油中会产生七种含量不同的气体[19]，将其中的氢气(H2)、甲烷(CH4)、乙烷(C2H6)、乙烯(C2H4)、乙炔(C2H2)的体积分数作为观察对象，依据在线监测的气体含量数据，可采用IEC三比值法[20]、四比值法[21](包括Dornenburg法，Rogers法，德国四比值法)、大卫三角形法[22]进行故障诊断，但故障编码不多，由于缺码的原因导致有些故障无法判断。本文采用无编码比值法，即直接由比值确定故障，不用将气体含量的比值进行编码，将变压器的故障区分为9种：低能放电兼过热MF1、高能放电兼过热MF2、局部放电PD、低能放电D1、高能放电D2、低温过热T1(<300℃)、中温过热T2(300～700℃)、高温过热T3(>700℃)、正常N。将以下特征气体浓度比值作为输入特征量：

CH4/H2，C2H2/C2H4，C2H4/C2H6，C2H2/(C1+C2)/%,H2/(H2+C1+C2)/%,C2H4/(C1+C2)/%,CH4/(C1+C2)/%,C2H6/(C1+C2)/%,(CH4+C2H4)/(C1+C2)/%

式中，C1为一阶碳氢化合物CH4；C2为二阶碳氢化合物C2H6、C2H4、C2H2体积分数之和，输入特征信息含量丰富，适用于SE-DenseNet深度神经网络。

4.2 故障类型独热编码

针对9种故障类型，采用one-hot编码。将MF1、MF2、PD、D1、D2、T1、T2、T3、N依次序编码为：[0,0,0,0,0,0,0,0,1],[0,0,0,0,0,0,0,1,0],[0,0,0,0,0,0,1,0,0],[0,0,0,0,0,1,0,0,0],[0,0,0,0,1,0,0,0,0],[0,0,0,1,0,0,0,0,0],[0,0,1,0,0,0,0,0,0],[0,1,0,0,0,0,0,0,0],[1,0,0,0,0,0,0,0,0]。针对本文探讨的分类问题，使用softmax交叉熵来作为目标函数的一部分。

5 WGAN的数据增强

WGAN是有监督的学习，本文使用WGAN将数据空间规模扩大，依据原始数据，生成特征一致，但数值不同、故障类型可以被识别为同一种类型的数据，以提高SE-DenseNet神经网络的泛化能力。

5.1 GAN的原理

生成对抗网络(Generative Adversarial Networks，GAN)[25]由生成器G和判别器D组成，生成器G将噪音数据生成为与真实数据分布相似的数据，并尽量骗过判别器，使判别器将生成的数据判断为真(1)。判别器的作用是辨别数据的真(1)伪(0)。因此使判别器不断的学习，以提高它的判别能力，让判别器效果更好，在生成器和判别器对抗学习中，最后判别器分辨不出生成数据的真伪，即生成的数据特征和真实数据的特征也就高度一致了，损失函数即为式(10)：

(10)

式中，x为真实数据；pdata(x)为真实数据分布；z为噪音数据；pz(z)为噪音数据分布；D(·)为判别器；G(·)为生成器。损失函数的功能是最大化D的判断能力，使最小化G和真实数据的分布之间的差异。判别器中使D(x)接近1，D(G(z))接近0，生成器中使D(G(z))接近1。Ex～pdata(x)和Ez～pz(z)表示真实数据和生成数据的概率,E表示期望。

5.2 WGAN的说明

WGAN中使用平滑的EM(Earth-Mover)距离，用梯度下降法优化参数时，可以提供梯度，实现两分布距离度量，在EM距离中加入李普希兹约束，使网络满足稳定性要求。以已知故障类型样本的五种特征气体含量为真实数据，从九种故障中任选一种，样本量10左右，在区间[-1，1]中随机选取服从均匀分布的噪音数据，将两者输入WGAN模型得生成数据gen_data，用关于gen_data的一次函数生成同种故障类型的样本数据data。总共生成1500条样本数据，为验证生成数据与原始数据特征一致性，预先使用1630条原始数据训练SE-DenseNet模型，再分别将生成的各种故障类型数据作为输入，得到的SE-DenseNet模型预测准确率如表2所示。

表2 生成数据作为输入的模型准确率Tab.2 Accuracy of model with generated data as input

表2的准确率为将生成的某一故障类型数据输入模型，重复预测12次得到的平均值。准确率最低的故障类型为正常，其值为86.72%，最高为低能放电兼过热，其值为98.43%，当将所有生成样本输入模型时得到的准确率值为90.41%，表2数据充分说明生成数据具有与原始数据一致的特征。

6 算例分析

本实验使用的软件框架为tensorflow 1.12，win10系统，硬件为intel core i7，1.80 GHz，内存16 GB，英伟达显卡MX-150,2 GB显存。本文使用某水电站的500/330 kV变压器的1 630条数据作为原始数据，使用WGAN生成了1 500条数据。将生成数据和原始数据合并成3 130条数据的样本集，两者随机充分混合后，按9∶1的比例分为训练集和测试集。运用t-SNE技术将样本数据进行可视化，得到初始分类效果如图5所示，可知未经SE-DenseNet模型特征提取处理的数据分类效果较为分散。

图5 原始分类效果Fig.5 Original classification effect

在CNN，Densenet和SE-DenseNet中，将数据输入各自模型，迭代300个epoch(每个epoch代表整个数据集完整处理一次)，可得训练集和测试集的准确率如图6和图7所示。

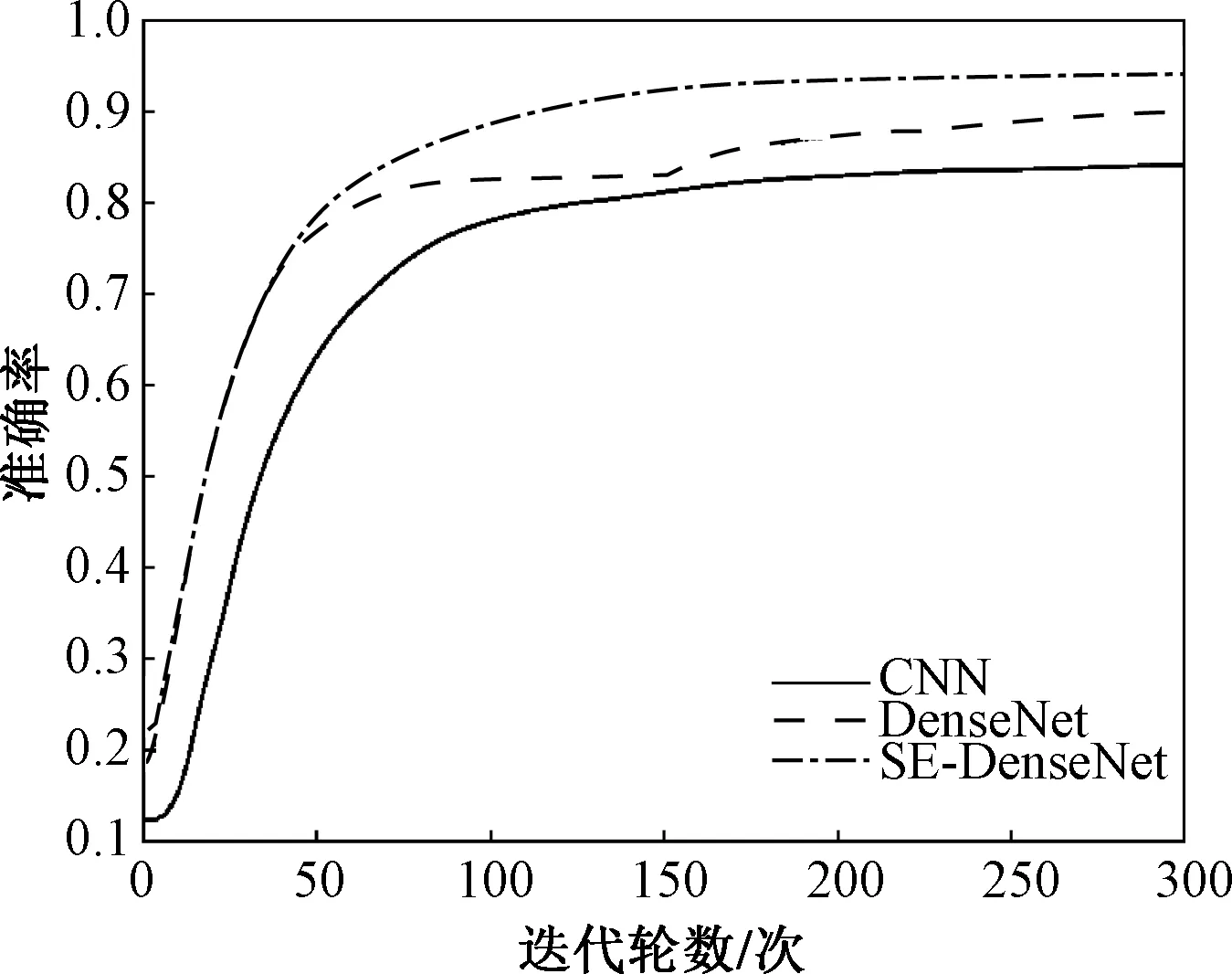
图6 训练集准确率图Fig.6 Accuracy graph of training set

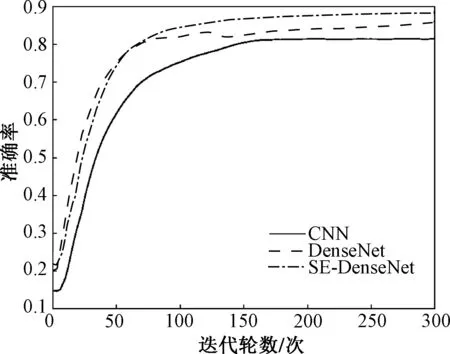
图7 测试集准确率图Fig.7 Test set accuracy chart

由图6和图7可知，CNN，Densenet，SE-DenseNet训练集、测试集准确率的最终收敛值如表3所示。

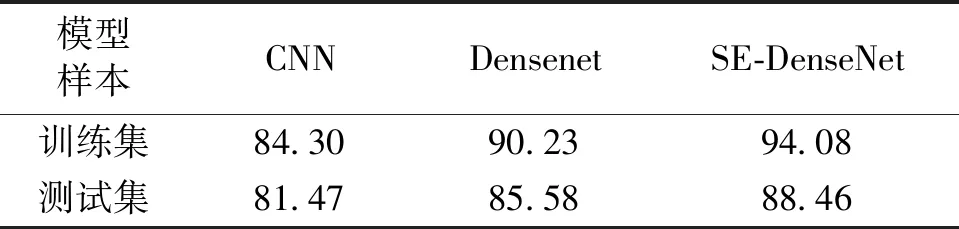
表3 各神经网络的准确率Tab.3 The accuracy of each neural network (%)

此处训练集样本量为2 816，测试集样本量为312。训练集准确率的定义是将单批次64个样本作为模型输入，共44个批次，将单批次的准确率累加，再除以44求得平均准确率。单批次准确率是模型评分logits向量中的最大值的索引号与真实标签(已转为独热编码向量)中的最大值索引号相等的次数之和除以单批次样本量。每44个批次为一回迭代轮数，共300回迭代轮数，模型采用最终收敛的平均准确率。测试集是单批次26个样本，共12个批次，其平均准确率同理可得。

由图6可知，当数据为训练集时，CNN、Densenet、SE-DenseNet分别在迭代220、250、200次后趋于稳定。通过观察可得Densenet准确率上升的速度最快，SE-DenseNet由于挤压和激励环节操作，准确率上升速度位居其次，在迭代48次后，SE-DenseNet的训练集的准确率高于Densenet，最终SE-DenseNet网络在训练集上的准确率为三者最高：94.08%，分别比DenseNet和CNN高出了3.85%和9.78%。由图7可知，当数据为测试集时，CNN、Densenet、SE-DenseNet分别在迭代160、135、140次后收敛，在迭代初期，Densenet准确率上升的速度最快，迭代65次后，SE-DenseNet的准确率高于Densenet，最终SE-DenseNet在测试集上的准确率为88.46%，在三者之中最高，分别比DenseNet和CNN高出了2.88%和6.99%。

CNN由于数据样本量不够，提取特征的能力相较于数据特征信息流通更为顺畅的DenseNet和SE-DenseNet较低，容易出现过拟合，所以准确率最低，SE-DenseNet由于在DenseNet基础上嵌入SE操作，使得网络能更快的学习到重要特征，降低了DenseNet网络融合数据特征时产生的冗余性，所以准确率最高。

从图8和图9可以看出SE-DenseNet模型在训练集和测试集上的最终损失值分别为0.270 1和0.605 8，由此得出SE-DenseNet损失值很小，说明SE-DenseNet模型预测很准确。

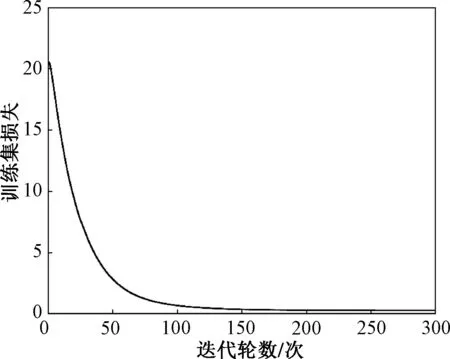
图8 SE-DenseNet的训练集损失函数下降图Fig.8 SE-DenseNet training set loss function decline graph

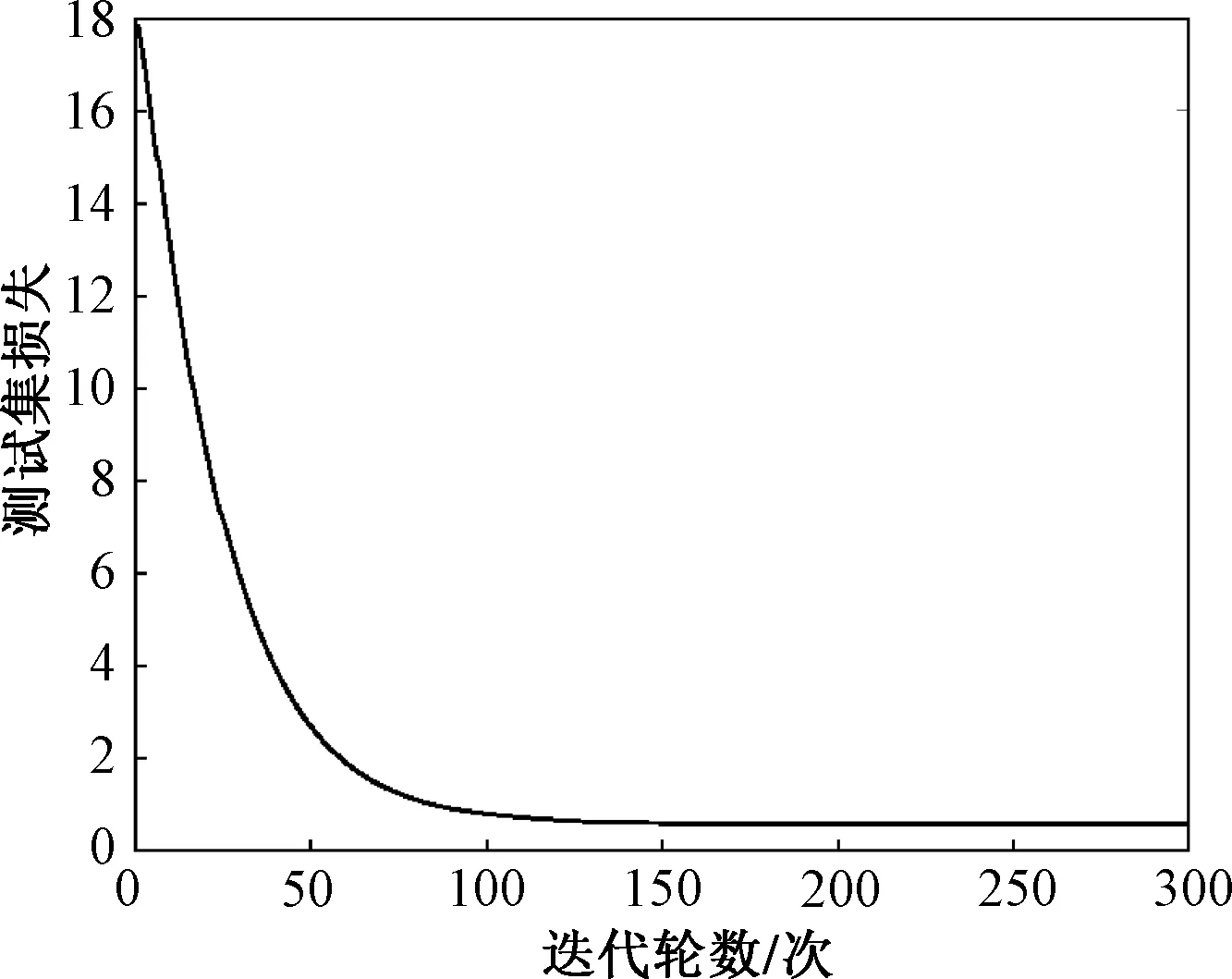
图9 SE-DenseNet的测试集损失函数下降图Fig.9 SE-DenseNet test set loss function decline graph

为了验证SE-DenseNet模型的优良的预测性能，将其与DenseNet在与本节上文同样的数据集的条件下进行训练对比，在测试集的结果如表4和表5所示。

此处准确率定义同表3，由表4可得模型改进后，在相同的网络层数下，SE-DenseNet比DenseNet测试集准确率都要高，平均高出1.504%，为验证模型的稳定性，继续对SE-DenseNet进行深层训练，由表4和5可得SE-DenseNet模型在56层时达到稳定状态，准确率维持在88.46%。经表4和表5的对比可知，由于SE模块的特征重标定，结合DenseNet的特征重复利用的优点，本文所提出的SE-DenseNet模型有着优良的性能和很高预测准确率。

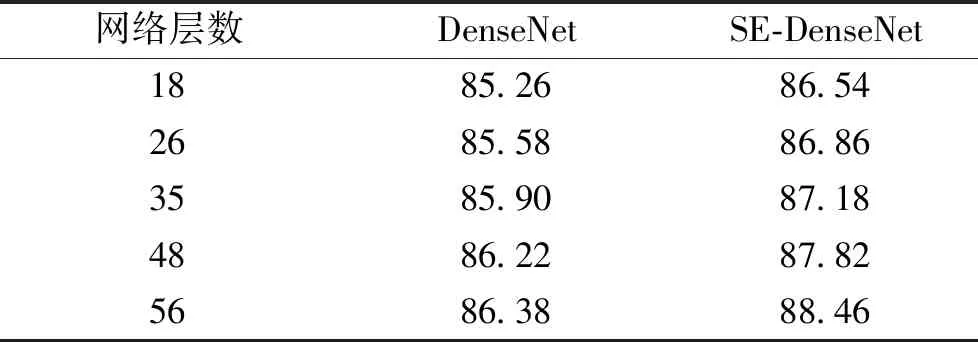
表4 模型改进前后测试集分类准确率对比Tab.4 Comparison of classification accuracy (%)

表5 深层SE-DenseNet测试集分类准确率Tab.5 Deep SE-DenseNet accuracy (%)

在每一单批次迭代过程中，经SE-DenseNet模型的特征提取后，将模型得到的评分数据logits输入softmax交叉熵函数之前，将评分数据logits保存至文档中，然后再进行分类训练。当评分数据迭代更新至第300轮，即分类训练结束时，将最终的评分数据提取出来并进行t-SNE的可视化，可得最终分类效果如图10所示。由图10可得经本文提出的SE-DenseNet模型特征提取后样本数据分类效果更集中。结合图6和图7、表3和表4中的数据对比以及对图8～图10的分析，可知本文提出的SE-DenseNet诊断模型收敛性能最好，泛化能力最强。

图10 最终分类效果Fig.10 Final classification effect

7 结论

针对变压器在已有故障数据条件下，故障类型难以判断、诊断准确率较低的情况，本文结合WGAN数据增强提出了SE-DenseNet模型，能准确细致地检测出故障数据与故障类型的内在联系，结论如下：

(1)基于无编码比值法原理的CNN，DenseNet，SE-DenseNet变压器故障诊断准确率普遍较高，SE-DenseNet加入了特征图校准权重的SE模块，抑制无用特征，增强有用特征，同时充分利用DenseNet的梯度流通顺畅，计算冗余性较低的优点，结合运用指数衰减学习率、dropout、L2正则化，运用Adam收敛算法，批量归一化及ReLU函数，经表3和表4的对比可知，相较于传统的CNN和DenseNet,本文提出的SE-DenseNet性能更好，预测准确率最高。

(2)无编码比值法在变压器的故障判断中，能将复合故障和单一故障区分开来，使模型判断能力得到很大的提高，泛化能力增强。在WGAN数据增强时，虽然生成了特征一致的同故障类型数据，但还可进一步研究关于生成数据gen_data的经验公式，以提高特征一致性程度和模型的预测准确率。

(3)SE-DenseNet神经网络模型的加深与样本空间规模的扩大有着密切联系，通过实验已找到本文数据集下SE-DenseNet具有最佳性能的网络层数，今后的工作将研究模型性能的提高与故障样本规模扩大之间的关联，以及使用更有效的迭代收敛算法，对原模型进行优化，使模型收敛速度更快，泛化能力更优秀。