基于差分-公共功率与滑模控制的直流互联交流电网振荡抑制
2021-02-01彭光强熊林云
李 清,彭光强,熊林云
(1. 中国南方电网有限责任公司超高压输电公司检修试验中心,广东 广州 510663;2. 重庆大学电气工程学院,重庆 400000)
1 引言
在传统电力系统中,区域内以及跨区域低频机电振荡通常由本系统中同步发电机惯量、阻尼系数、电力系统调节器以及励磁控制系统所决定的。因此,已有诸多针对传统电力系统的功率振荡抑制的研究[1-5]。而相关功率振荡抑制方法也可运用于高压直流(HVDC)输电系统中。早期的研究通常基于电流源型变流器,而近些年基于电压源型变流器(VSC)的功率振荡抑制方法得到了越来越广泛的关注,如文献[6-8]提出了一系列基于VSC-HVDC互联的电力系统低频振荡抑制方法。
在现代电力系统中,含电力电子器件的可再生能源装置逐步替换传统发电厂。然而,基于传统控制策略的电力电子变换器难以为系统提供相应的物理惯量,而系统等效惯量的降低会在严重扰动情况下危及系统安全性。因此,亟需研究电力电子变换器渗透主网引起的功率振荡问题。为补偿系统缺失的惯量,文献[9-12]提出了一系列控制策略用于模拟HVDC系统中同步电机的动态特性并用于改善系统的频率稳定性。然而,在大多数情况下,这些控制方法都假定直流电压控制与同步电机动态处于同样的时间尺度,因而可能会影响系统的直流电压稳定。
为提高多电力电子电力系统的频率振荡抑制能力,诸多学者提出了采用HVDC联络线的控制方法抑制系统振荡,而这些方法通常都不考虑多电力电子电力系统中的惯量缺失问题。如文献[7]提出了一种针对离岸风电场HVDC联络线功率振荡的控制方法;文献[13]提出了一种基于FACTS装置与的协同控制策略用于抑制跨区域低频振荡;文献[14]提出一种基于有功功率调制的含多HVDC联络线的区域内振荡抑制方法。此外,基于广域信号测量的功率振荡抑制方法也得到了广泛关注,如文献[15]提出了一种基于广域信号测量与线性二次型高斯调节器的振荡抑制器;文献[16]提出一种基于监督控制器与实时频率测量信号的跨区域振荡抑制方法;而文献[17]提出了一种鲁棒控制器用于解决局部以及全局通讯中断情况下的跨区域振荡抑制问题。这些方法在一定程度上能够有效抑制系统功率振荡,然而其都需要稳定快速的通讯网络,因而增加了系统的复杂度且降低了系统可靠性;文献[18]则提出了一种广域信号测量中含通讯延迟的控制器用于抑制跨区域振荡。而为降低对HVDC母线之间高带宽通讯网络的依赖,有学者提出通过直流母线电压变化来反映交流电网频率波动的方法,并设计了相应的振荡抑制控制器。文献[19]首次提出了一种不需要通讯网络的功率振荡抑制器,其运用于离岸风电场并通过VSC-HVDC联络线为交流系统提供虚拟惯量。
本文旨在提出一种基于差分-公共功率与滑模控制的交流电网振荡抑制方法。首先引进交流电网之间的虚拟机电摩擦的概念,并提出一种针对VSC型HVDC联络线的振荡控制器。随后建立互联电力系统的转子摇摆方程等效模型,并通过本控制策略为HVDC联络线两端系统提供调频以及频率振荡抑制服务。其中,引进了差分-公共功率的概念以实现本控制方法,进而实现了对HVDC联络线的直流电压与功率传输的解耦控制。随后,通过滑模控制改进两个等效发电机对参考转速的追踪性能,因而保证系统在发电功率波动情况下的控制器鲁棒特性。本控制方法结构简单、易于实现,且无需HVDC两侧变换器之间的通讯联络,因而降低了对高带宽通讯网络的依赖。最后,通过仿真算例验证了本方法的有效性。
2 系统模型
2.1 参考系统模型
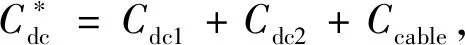

图1 含HVDC联络线的互联等效电力系统控制框图Fig.1 Control diagram of equivalent power system with HVDC connection
以等效发电机G1为例,其线性化摇摆方程可以用如下状态方程描述(本方程对于发电机G2同样适用)[20, 21]:
(1)
式中,H1为本区域等效惯性常数;ω1为本区域角频率;Δ为增量符号;Pm1为机械功率;Pe1为本区域负荷;D1为本区域等效阻尼系数。其中,Pm1由一个等效发电机速度调节器控制,其由一个一阶低通滤波器表征。而发电机速度调节器的频域形式动态方程为:
(2)
式中,P*和ω*分别为有功功率与角频率参考值。为简化分析,在后续计算中省略增量符号Δ。
上述模型为传统交流电网的一个简化模型,其由一个二阶系统表征。因此,本模型能够很好地描述本文引进控制系统的耦合效应,且本模型将用于表征HVDC终端测量所得的频率振荡。
2.2 差分-公共功率概念
本文所提出的差分-公共功率的概念如图2所示,其运用于一对背靠背VSC变换器中。差分-公共功率分别定义为:
pcm=-(po1+po2)
(3)
(4)
式中,po1和po2分别为线路经VSC1和VSC2注入交流电网1和交流电网2的有功功率;pcm和pΔ分别为公共功率与差分功率。两个新变量的优势在于:其可以将决策直流母线电压动态的有功潮流与网络G2向G1流动的有功潮流相解耦。因而,采用式(3)和式(4)所示定义后,可以实现如下功能:
(1)通过控制公共功率量pcm实现对直流母线电压的快速精确控制。
(2)通过控制差分功率pΔ实现控制两台等效发电机之间的虚拟机电摩擦。
此外,通过式(3)和式(4)可以得出两个等效系统对应的输出功率,分别为:
(5)
(6)
式(5)和式(6)将用于计算两个VSC对应的参考功率。

图2 基于差分-公共功率的背靠背VSC潮流分布图Fig.2 Power flow distribution of back-to-back VSC with common-differential power
3 虚拟摩擦概念
3.1 差分功率及其等效机械模型
在以上提出的概念中,若不考虑功率损耗以及LCL型滤波器中储存的能量,差分功率pΔ则对应于两个网络之间的有功功率交换。而差分功率可等效为两个交流网络之间的机械摩擦,因此,定义如下变量:
(7)

图3 本文所提虚拟摩擦以及公共功率电压控制器Fig.3 Virtual friction and common power controller proposed in this paper
当差分功率控制器的暂态响应明显快于等效电机G1与G2时,在系统层分析时其动态特性可以忽略。因此,差分功率可以表示为如下形式:
(8)
此外,忽略功率损耗时,有Pe1=-po1,Pe2=-po2。将式(5)和式(6)代入式(1),有:
(9)
(10)


图4 本文所采用互联电力系统模型Fig.4 Interconnected power system model utilized in this paper
3.2 基于公共功率的直流电压控制器
当忽略线路功率损耗以及储存于LCL滤波器中的能量时,直流母线电容器中存储的功率具有如下动态特性。
(11)
值得注意的是,因公共功率pcm与直流电容所储存的能量之间有着直接的联系,因而可以通过图3(b)所示的PI控制器对公共功率进行控制以进一步实现对直流电容电压的控制。
4 基于滑模的等效电机控制
4.1 基于滑模控制的等效电机转速控制
为保证等效电机G1与G2精确追踪其参考转速,采用滑模控制方法实现对G1与G2转子转速的控制。针对式(9)和式(10),构造如下追踪误差变量。
(12)

(13)
(14)
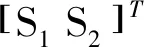

(15)
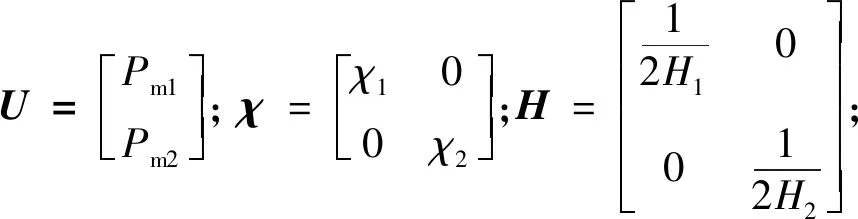
选择如下滑模控制趋近律:
(16)
式中,K为对角元素全为正的对角矩阵;0<ζ<1;D(S)为关于S的函数,其具体形式为:
D(S)=λ+(1-λ)e-β|S|
(17)
式中,0<λ;β<1。当采用式(16)时,能够最优化滑模控制器的综合控制性能,即当状态变量轨迹距离滑模面较远时,加速状态轨迹的趋近速度;而当状态变量轨迹逼近滑模面或在滑模面两侧反复穿越时,符号函数前的增益系数较小,因而能够最大程度降低滑模控制的抖振幅值。因而,本趋近律具有较好的控制性能。
将式(16)代入式(15),可得两台等效发电机转速控制输入为:
(18)
4.2 有功-无功功率与电压控制器
(19)
式中,Ddc为直流电压下垂系数。将系统1与系统2的输出功率相减后,有如下式:

(20)


图5 对应VSC1的直流电压与虚拟摩擦控制器框图Fig.5 Control diagram of DC voltage and virtual friction control for VSC1
在图2所示系统中,两个VSC都能够对直流电压进行控制,因而,在设计直流电压控制器时,应当避免使用两个积分运算。因而,设计如下的比例控制器:
(21)

(22)
随后计算有功-无功功率控制器的参考电压。本文所提控制器参考电压计算过程如图5(c)所示,通过图5(c)可以计算出pΔ与pcm参考值。进而可以通过式(5)和式(6)得出有功功率参考值,如下:
(23)
(24)
而注入两端系统的无功功率可采用下式进行独立设定并控制:
(25)

综上,本文所提基于虚拟摩擦与滑模控制的区域间频率振荡抑制方法如图6所示。

图6 基于滑模控制与虚拟摩擦的频率振荡抑制方法Fig.6 Proposed frequency oscillation damping method based on sliding mode control and virtual friction
5 仿真验证
5.1 仿真平台与参数选择

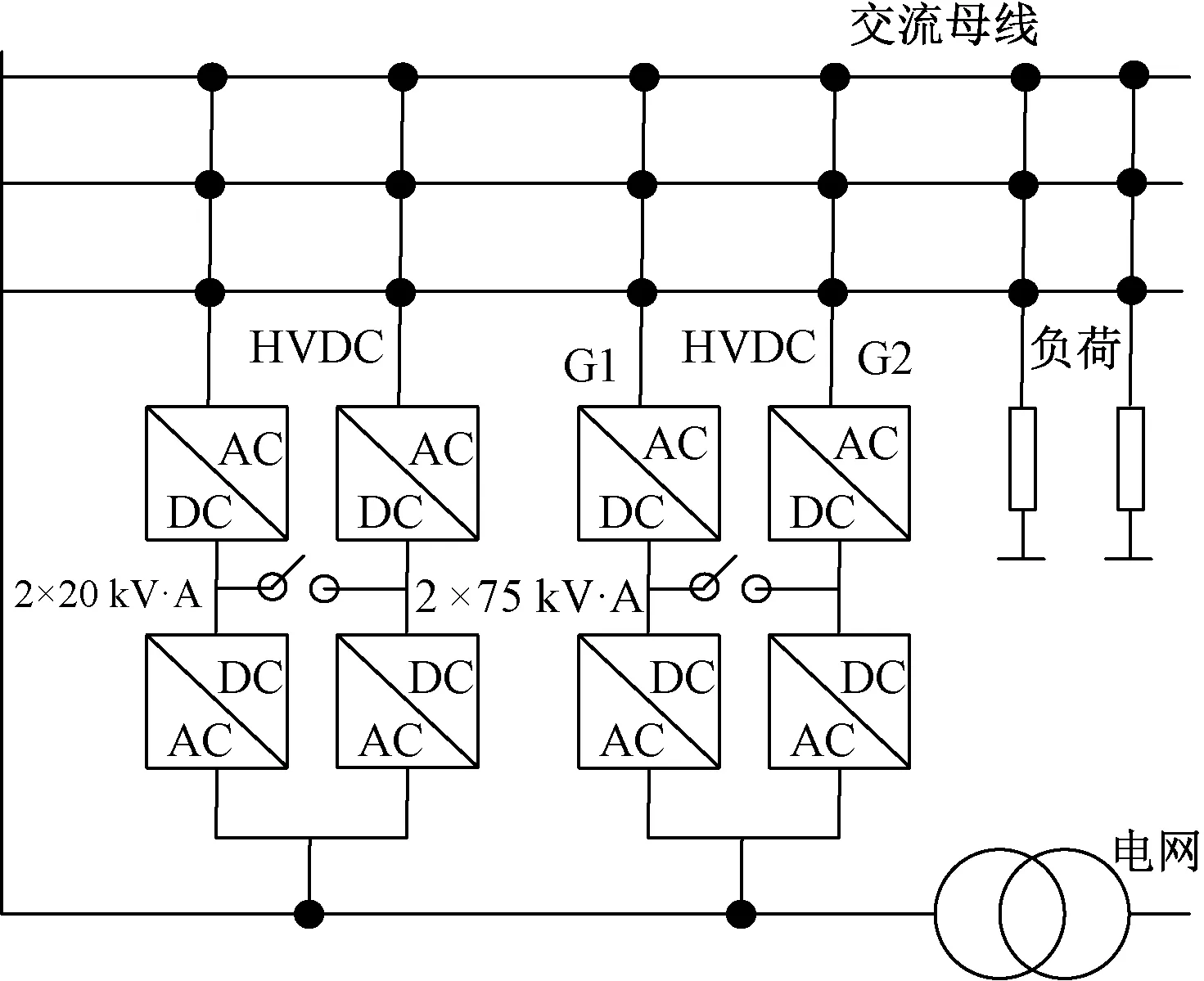
图7 本文采用的交流系统仿真平台Fig.7 AC system simulation platform utilized in this paper
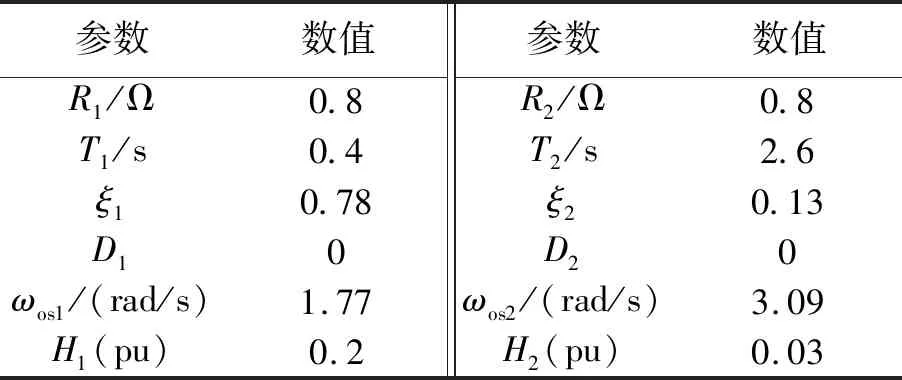
表1 发电机等效模型参数Tab.1 Parameters of the generator equivalent model
5.2 虚拟摩擦概念验证
为验证本文所提虚拟摩擦概念对于本系统的有效性和意义,需要研究其虚拟摩擦增益Bω对于系统等效电机G1和G2振荡的影响。图8为在不同增益值下两个等效电机传递函数ω1(s)/Pe1(s)与ω2(s)/Pe2(s)的波特图。当引进虚拟摩擦增益Bω后,会在两个系统之间建立耦合关系。而当Bω增大时,G2的谐振峰值会逐渐减小。

图8 不同虚拟摩擦值下传递函数波特图Fig.8 Bode diagram of transfer function with different values of virtual friction
图9为等效系统2中出现负荷阶跃变化时两个系统在不同Bω数值下的暂态响应曲线。当Bω=0时,两个系统处于解耦状态,且系统2处的负荷阶跃变化造成了较为严重的频率振荡现象。而当Bω的取值大于0时,两个系统之间通过虚拟摩擦进行耦合,因而系统2处的负荷阶跃变化能够由两个系统共同承担,进而降低频率振荡强度。此外,从图10(b)可以看出,当Bω数值增大时,两个系统之间的耦合强度增加,因而系统1能够承担更多的负荷增长量,并有效抑制两个互联系统之间产生的频率振荡。
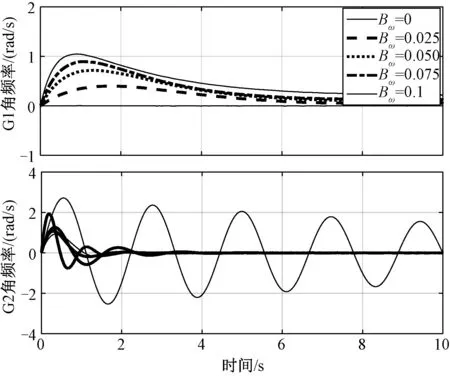
图9 G2出现负荷阶跃变化时两个网络的暂态响应曲线Fig.9 Simulation results of transient response of two grids with load step change in G2
5.3 弱阻尼下振荡抑制性能评估
为验证本文所提有功-无功功率与电压控制器的控制性能,考虑两台发电机中G2处于弱阻尼模式下的仿真。系统参数仍采用表1所示参数,并可计算出系统的最小阻尼系数,其为Bω的函数。同时,通过选取虚拟摩擦Bω的值最大化系统的阻尼系数。在本算例中,虚拟摩擦的最优值设置为Bω=0.05。通过设定不同的阻尼比以及参考功率值,两台等效电机仿真结果如图10和图11所示。

图10 不同虚拟摩擦值下微分功率参考值产生阶跃变化时两台等效发电机的暂态仿真曲线Fig.10 Transient simulation results of two equivalent generators with step change in differential power reference value at different virtual frictio

图11 不同虚拟摩擦值下G2负荷发生阶跃变化时两台等效发电机的暂态仿真曲线Fig.11 Transient simulation results of two equivalent generators with load step change in G2 at different virtual frictions
在图10中,图10(a)为两个系统间不存在虚拟摩擦时,系统差分功率参考值产生阶跃变化时两台等效发电机的暂态仿真曲线。由图10(a)可以看出,系统差分功率能够快速跟踪参考值变化,且G1显示出较好的振荡阻尼特性。然而,当参考有功功率变化时,发电机G2表现出较差的振荡阻尼性能,并产生了较为明显的振荡。同理,图11(a)为不含虚拟摩擦情况下,G2本地负荷突增情况下的暂态仿真曲线。由图11(a) 可以看出,G2同样表现出较差的振荡阻尼特性,这与4.2节的分析结果保持一致。
图10(b)为虚拟摩擦Bω=0.05且差分功率参考值发生阶跃变化时的仿真曲线。此时,通过提出的虚拟摩擦以及转速滑模控制器用于建立两台发电机之间的耦合关系,并采用3.2节的有功-无功功率控制器实现两个系统之间的功率交换。在图10(b)中,差分功率能够根据交流电网的频率动态特性表现出快速的暂态响应,并防止低频振荡的产生。同时,通过两个系统之间的直流电压实现信息交互,以实现对于有功功率缺口的响应。图11(b)为虚拟摩擦系数维持在Bω=0.05时,G2系统出现负荷阶跃变化时的仿真结果。当G2出现负荷突增时,差分功率能够表现出较强的暂态特性,并导致有功功率由G1向G2流动以满足负荷需求,进而抑制低频振荡。在图10(b)和图11(b)两个算例中,直流电压都表现出了一定的信息共享特性,其暂态特性直接反应交流系统的频率变化,因而其能够用于决策某一端口的有功功率缺口。
5.4 发电功率波动下振荡抑制性能对比
为验证本文所提基于滑模控制在发电功率波动情况下的振荡抑制性能,将其与基于PI控制的振荡抑制控制器进行对比。在本算例中,PI控制器参数与滑模控制器参数都通过静态调参使其保持最优控制性能,由此得出的仿真结果如图12~图14所示。在图12~图14中,两个系统中都出现10%额定容量的负荷突增,且发电机发电功率出现不同程度的波动。其中,图12表示系统1发电功率突降5%情况下的仿真曲线;图13表示系统2发电功率突降5%的仿真曲线;图14表示系统1和系统2发电功率同时突降3%情况下的仿真曲线。由差分-公共功率的定义式(3)和式(4)可知,系统的瞬时发电功率改变时将会改变差分-公共功率的值,进而改变控制器中对应参数值。此时,对于系统鲁棒性有较高要求。

图12 系统1发电功率突降5%情况下的仿真曲线Fig.12 Simulation results when there is a 5% generation capacity decrease in system 1

图13 系统2发电功率突降5%的仿真曲线Fig.13 Simulation results with 5% generation capacity decrease in system 2

图14 系统1和系统2发电功率同时突降3%情况下的仿真曲线Fig.14 Simulation results with 3% generation capacity decrease in system 1 and system 2
由图12~图14可知,当出现负荷突增时,两个系统都会出现不同程度的频率振荡。而由于本文中差分功率以及公共功率作为控制器的参数存在,其受控制器本身鲁棒性影响。从图12~图14所示仿真结果可以看出,当两个区域中任一区域出现发电功率跌落时,采用滑模控制方法的控制性能优于传统PI控制方法。由图12可以看出,采用滑模控制时,G1频率振荡幅值明显小于采用PI控制器的振荡幅值;由图13可知,当采用PI控制时,G1频率响应曲线调节时间为22 s,而当采用滑模控制时,调节时间为9.1 s,较PI控制有明显改善;而从图14中G1频率响应曲线可以看出,采用滑模控制时其调节时间以及频率振荡幅值较PI控制都有明显改善,由此体现出滑模控制较强的鲁棒性。
6 结论
本文提出了一种基于差分-公共功率与虚拟摩擦的HVDC互联交流电网振荡抑制控制方法。首先建立两个交流系统之间的等效模型,并引进差分-公共功率的概念,其能够有效表征两个交流系统的功率波动,并作为控制器参数用于响应系统负荷波动。随后,引进虚拟摩擦的概念用于表征两个系统之间的功率交换。同时,将直流电压作为衡量两个交流电网频率波动的指标,因而避免了两个交流系统之间的通讯。随后,提出了基于滑模控制的等效发电机转速控制方法,用于改善系统对于发电功率波动的鲁棒性。通过仿真算例,验证了虚拟摩擦概念的有效性;同时,验证了本文所提控制器在弱阻尼下的振荡抑制性能;最后通过等值发电机功率突降的算例验证了本文所提控制器的鲁棒性。
