潜堤上规则波辐射应力的数值研究

穆浩然马小舟毛艳军高 翔

(1.大连理工大学 建设工程学部,辽宁 大连116024;2.海岸和近海工程国家重点实验室,辽宁 大连116024)

辐射应力概念最初是由Longuest-Higgins和Stewart[1]提出并给出了适用于计算微幅波辐射应力值的简化公式。在近岸波浪的传播运动中,由于海水深度变浅导致了波浪产生严重变形甚至破碎,从而引起辐射应力的强烈改变,辐射应力变化对沿岸波生流、波浪增水(set-up)、波浪减水(set-down)有着重要影响,也是低频波浪生成的重要驱动力。Longuest-Higgins和Stewart[2]认为波浪辐射应力的增加将促使波群中自由长波的释放;Symonds等[3]建立了控制方程中含有辐射应力受迫项的碎波拍模型,认为波群中波浪破碎点前后移动引起辐射应力在时间及空间上的改变产生了低频波浪;Kostense[4]定性地验证了短波群波浪破碎点移动导致低频波浪产生的理论。因此,为了更加准确地了解辐射应力这一波浪特性,众多学者通过理论分析,数值和实验模拟的手段进行辐射应力的计算。对于常水深Graham[5]提出用有限差分法计算辐射应力张量;郑金海和严以新[6]利用线性波理论研究波浪辐射应力张量随深度变化的分布规律,并给出适用于任意波向角的辐射应力的表达式;Xia等[7]提出了辐射应力垂向剖面的定义和计算公式,并利用斜坡上波生流的实验结果证明了模型的准确性;Stive和Wind[8]利用实验数据,通过线性外推法近似求得湍流波浪速度剖面来计算辐射应力沿程变化;温秀媛等[9]利用改进色散关系的Boussinesq方程推导出了全新的辐射应力计算公式,探究辐射应力对波浪增减水的影响。然而,上述辐射应力计算方法都难以获得碎浪带内详细的流场信息,并存在着一定程度的条件假设和公式简化,因此计算所得辐射应力结果误差较大。

基于OpenFOAM[10]软件开源程序建立数值水槽则是模拟波浪破碎区流场信息的一个较为可行的手段,可以详细研究完整计算域内波浪辐射应力随波浪传播而产生的变化过程。查晶晶和万德成[11]基于OpenFOAM软件进行的数值造波实验验证了此数值方法造波和消波方式的可靠性;王东旭等[12]利用此软件较好地模拟了孤立波在潜礁上的波浪破碎及水跃现象;毛艳军等[13]应用Open FOAM软件求解了箱式浮式防波堤的水动力性能,并分析了其作为垂荡浮子式波能转换装置的能量转换性能;姚宇等[14]运用Open-FOAM软件模拟孤立波在岛礁地形的传播,数值输出的破碎区内波形及流速与实验结果对比良好;张陈浩和郑茜[15]利用OpenFOAM软件模拟规则波在浅滩上的破碎变形,模拟结果与实验结果相吻合,且输出了能较好体现波浪破碎整体过程的流场信息。

本文拟应用OpenFOAM软件来模拟波浪在潜堤地形下的传播破碎,在进行平底水槽线性波的数值模拟和数值模型模拟波浪的准确性及计算辐射应力方法的有效性验证后,进行规则波在潜堤地形下传播破碎的模拟研究,在此基础上对辐射应力沿程变化的特点及其对波浪增减水的影响开展了研究,并探讨了平底地形下辐射应力与波幅偏移量之间的关系。

1 理论基础

1.1 控制方程

本文采用基于Open FOAM软件的造波模块waves2Foam[16]开展波浪传播变形的数值模拟。坐标系统为笛卡尔坐标系,x方向为波浪的入射方向,y方向为垂向,z方向为沿水槽的宽度方向,基于不可压缩流体的运动特点,控制方程为:

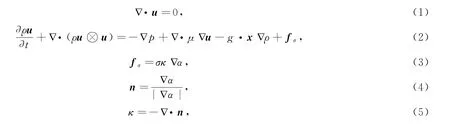
式(1)～式(5)中,ρ为混合流体的密度;u为流体的速度场;t为时间;μ为动力黏性系数;g为重力加速度;x为位置矢量;fσ为自由表面的张力;σ为张力系数;κ为自由表面的平均曲率;n为界面单位法向量;α为流体体积分数。

对于自由表面的处理,根据VOF法将2种流体看作一种混合流体,实现每个单元相界面的追踪,引入相函数:

在求解时,式(2)中的混合流体的密度ρ可用液体密度ρ1和气体密度ρ2表示,动力黏性系数μ可用液体黏性系数μ1和气体黏性系数μ2来表示:

同时,α满足输运方程:

传统的VOF法需要反复地进行自由表面的重构,降低了计算效率,因此Weller[17]引入了额外的人工压缩项来实现对自由水面的精确捕捉,式(9)可变为

式中:uc为适用于压缩自由面及调整自由面尖锐程度的速度场,新增加的人工压缩项只对界面过渡区起作用,不会影响到周围流场。

1.2 辐射应力公式

将作用于单位面积水柱体的总动量流的时均值减去没有波浪作用时的静水压力定义为波浪辐射应力。Longest-Higgins和Stewart[18]给出的水平x方向辐射应力(S xx)的定义公式为

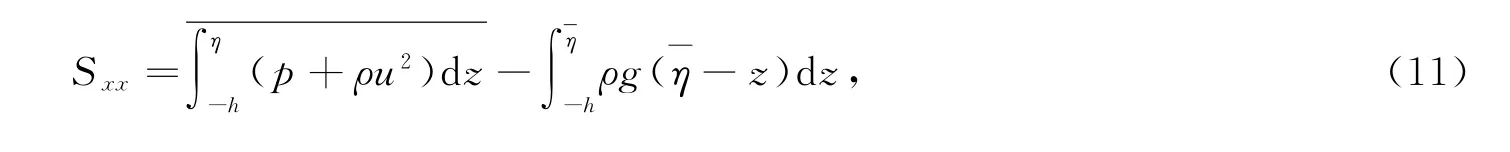
式中:u为质点速度在x方向的分量;h为水深;η为水面高程;i为平均水面高程;p为总压。

对于微幅波,辐射应力计算公式可简化为

2 模型验证

2.1 波形验证

表1 不同工况下的网格尺寸Table 1 Sensitivity analysis of grid size

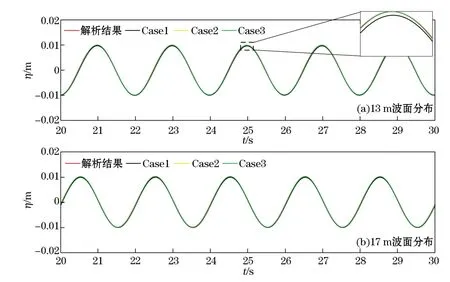
图1 不同网格尺寸下波面变化与解析波面对比Fig.1 Comparison diagram of wave surface between experimental results and numerical simulation with different grid size

将模型作用于模拟平底水槽中线性波的传播,其模拟工况为:波高0.02 m,波周期2 s,水深1 m,计算域长30 m,高1.1 m,数值水槽前端和后端各设置6 m松弛区(消波),模拟计算时长30 s,采用自动调整计算时间步长的方法,设置输出时间步长Δt=0.02 s。模型应用Case1,Case2和Case3三种不同大小的网格设置来进行敏感性分析,具体网格尺寸见表1。不同网格尺寸下波面对比如图1所示,由图可见,Case1网格尺度下模拟的波浪波峰值明显低于解析结果,由此产生的误差将影响到之后的数值计算,而Case2和Case3网格尺度下模拟的波浪则与理论解对应很好。因此,为保证波浪辐射应力计算结果的准确性并且能够节约计算资源,本文采用Case2网格尺寸进行模拟计算。得到了较好的数值模拟结果,其波面与理论波面的运动趋势及波峰波谷值均吻合较好,误差较小,由此说明本文所用数值模型可以很好地模拟波浪运动。

2.2 辐射应力计算结果验证

将上述工况中数值模拟计算的辐射应力沿程变化结果与微幅波理论下辐射应力结果进行比对,对比结果如图2所示。由式12和式13计算得到微辐波理论下的辐射应力值为0.4709 N/m,数值模拟结果中辐射应力值有较小幅度的振荡,可能是由波浪沿水槽传播过程中波幅产生微小差异所致,但整体而言,本模型模拟结果与理论结果对应得较好,说明本数值模型模拟波浪运动输出的流场、压力场较准确,辐射应力计算方法也是可行的。

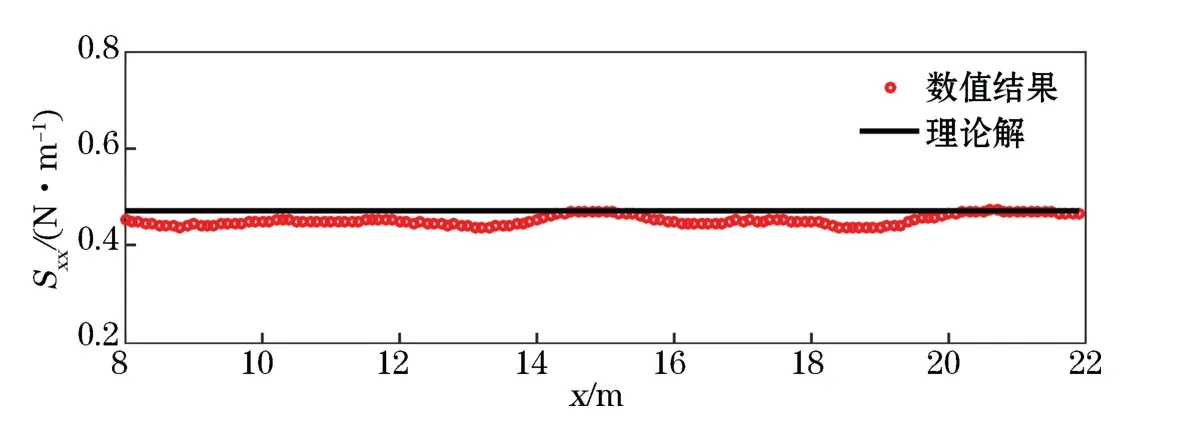
图2 平底水槽中数值模拟辐射应力值及微辐波理论辐射应力结果对比Fig.2 Comparison of numerical simulation and airy wavetheory results of radiation stress at flat tank

3 潜堤地形下辐射应力计算及波浪增减水模拟

潜堤地形的实验案例采用Beji和Battjes[19]的实验地形及工况,数值模拟Case A和CaseB两种工况下波浪的传播,并计算辐射应力及波浪增减水的沿程变化情况。本文采用层流模型来进行数值计算,利用相对较小的网格尺度进行波浪破碎的求解,能够得到较好的波浪模拟结果,且与湍流模型RANS相比,层流模型计算所得的破波区内波浪运动与实际波浪运动更为相似,能更好地模拟出波浪的破碎形态和波浪破碎后波面的起伏振荡现象,由于篇幅有限,在此不作更多的说明。数值模型布置如图3所示,堤顶高度为0.3 m,波浪沿水槽正向传播。数值模拟计算域长40.0 m,前后各设置8.0 m松弛区,计算时长为50 s,CaseA,CaseB均采用自动调整计算时间步长的方法,输出时间步长分别为Δt=0.02 s,Δt=0.025 s。总网格量均为80万,x方向网格尺寸为0.01 m,y方向网格尺寸为0.0025 m。数值模拟实验工况如表2所示。

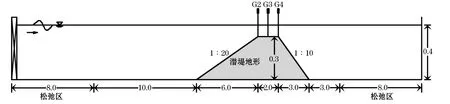
图3 潜堤地形布置(m)Fig.3 Layout of the submerged bars(m)

表2 潜堤地形实验工况列表Table 2 List of experimental cases of submerged bars topography

3.1 波形对比

当波浪传播到潜堤前坡坡顶位置时,非线性效应达到最大,波浪发生明显的破碎。将堤顶G2,G3和G4三处波面的时间变化曲线与实验结果对比,结果见图4,可以看出,在波浪初破阶段,Case A和CaseB工况的G2,G3处数模波峰波谷值与实验结果对应较好;在波浪完全破碎后(G4),2个工况的数值模拟计算结果均出现了低估峰值和谷值的现象。但是数值模拟的两工况的整体运动趋势,特别是破碎后波浪振荡趋势与实验现象基本一致,说明该数值模型可以较好地反映实验中波浪破碎后的实际运动,模拟的波浪破碎具有较大的可信度。图5给出了潜堤堤顶位置(24～26 m处)波浪破碎时的流场信息,可以清楚地看到,当破碎发生时,破碎点周围水质点的速度方向均指向破碎点处,越靠近破碎点的水质点速度值越大,在破碎波面处水质点运动最为剧烈,速度值达到最大。而距离破碎点较远的流场中,水质点速度较小,水体流动较为温和,但是受前一破碎波浪的影响,水体中水质点移动较为混乱,方向具有不确定性,这与波浪运动的实际情况较为符合,因此本数值方法计算所得流场信息较为可信。

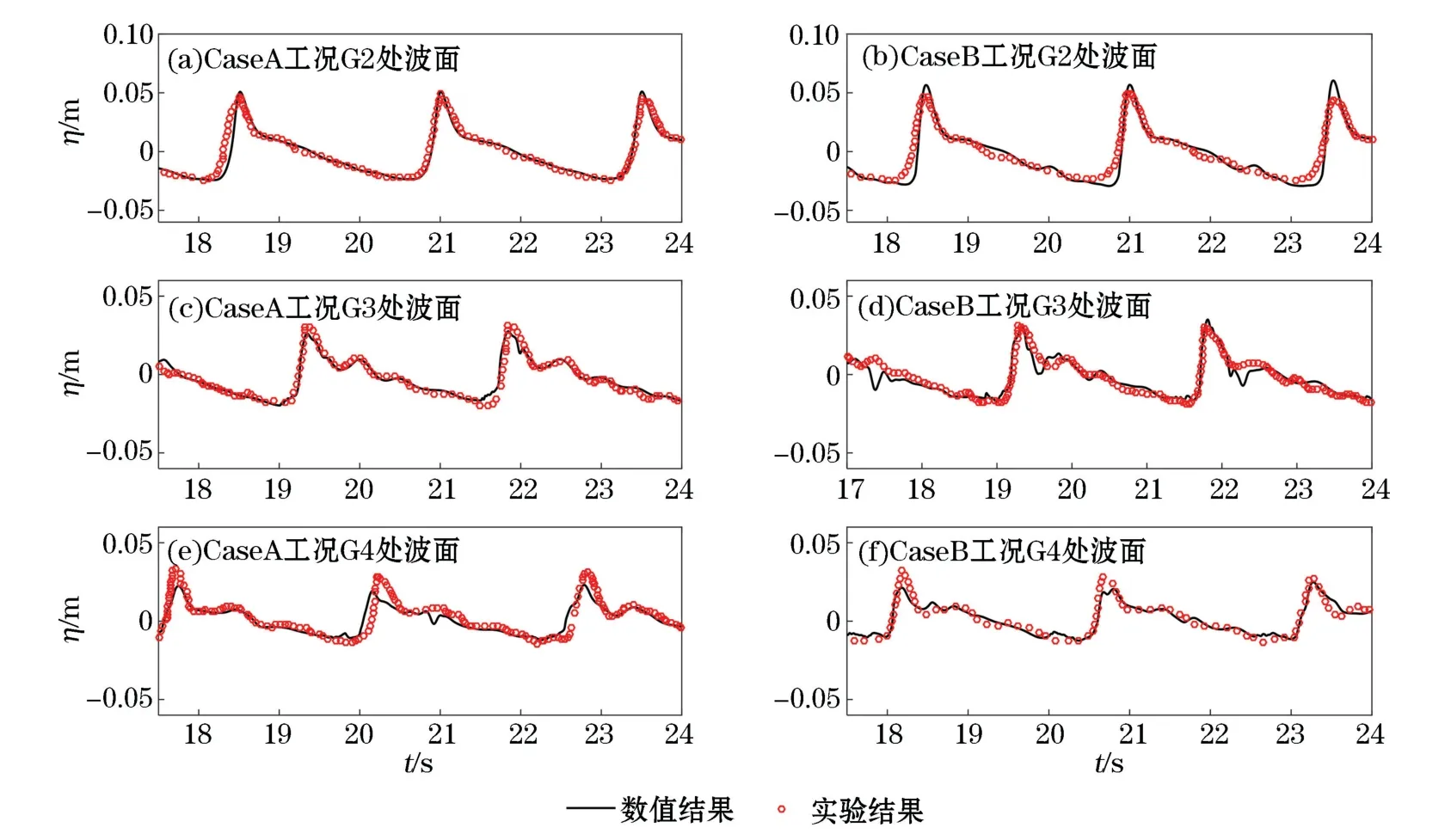
图4 CaseA和CaseB两种工况下G2、G3、G4处波面对比Fig.4 Comparison of wave surface at G2,G3 and G4 under CaseA and CaseB

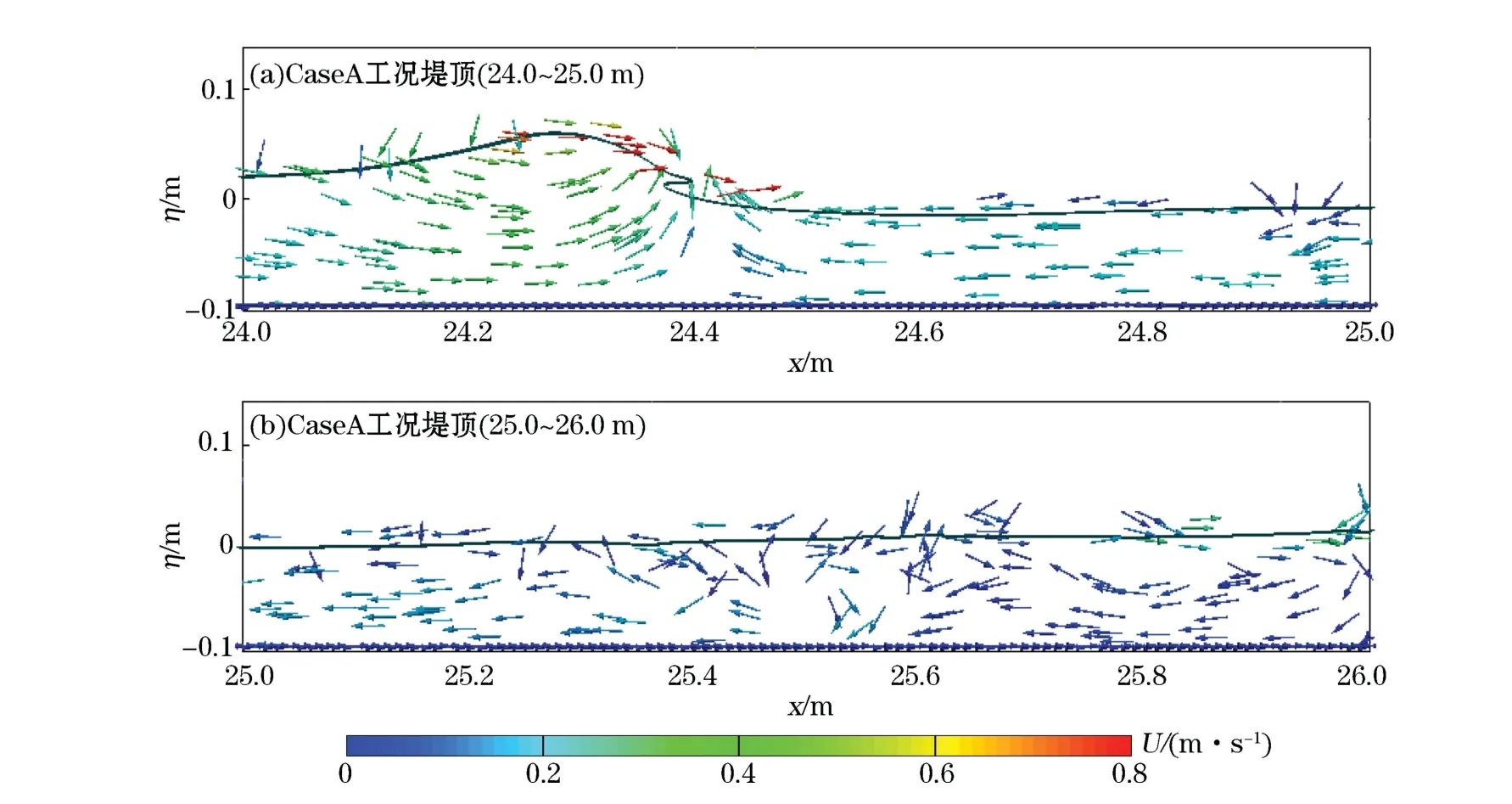
图5 Case A工况堤顶位置流场分布Fig.5 The flow field distribution at the top of the dam under Case A

3.2 辐射应力与波浪增减水

当波浪传播到潜堤区域时,会发生浅水变形并最终产生破碎,继而波高骤降,波浪动量减小,辐射应力将沿程发生变化,进而影响平均水平面的改变,这一波浪平均水平面的变化便称为波浪的增减水。当规则波沿x方向正向入射时,依据波浪增减水方程可知:

当辐射应力(S xx)沿程增长,即时,则波浪将产生减水现象;当辐射应力沿程降低,即时,则波浪将产生增水现象。波浪增减水的值即为波面升高的时均值与静水面位置的差值。本文根据数值模型输出的波面数据,进行周期内时间平均,得到Case A和CaseB两个工况下的波浪增减水变化。

图6和图7给出了潜堤地形下2种工况的波浪辐射应力和波浪增减水的沿程变化曲线。2个工况均能明显看出,当波浪传播在堤前平底时,辐射应力基本呈稳定值,到潜堤前坡坡底附近其值开始增大,直至堤顶处达到最大值,随后产生下降的趋势,在潜堤后坡面处由于水深的增加,辐射应力值再次增大,直至堤后平底水槽处趋于平稳。而波浪增减水的沿程变化趋势恰好与之相反。由于波浪完全破碎,波浪成分不稳定,在堤后坡面至平底处的辐射应力和平均水平面均有明显震荡,但是整体变化趋势依旧能较好地满足波浪增减水方程。

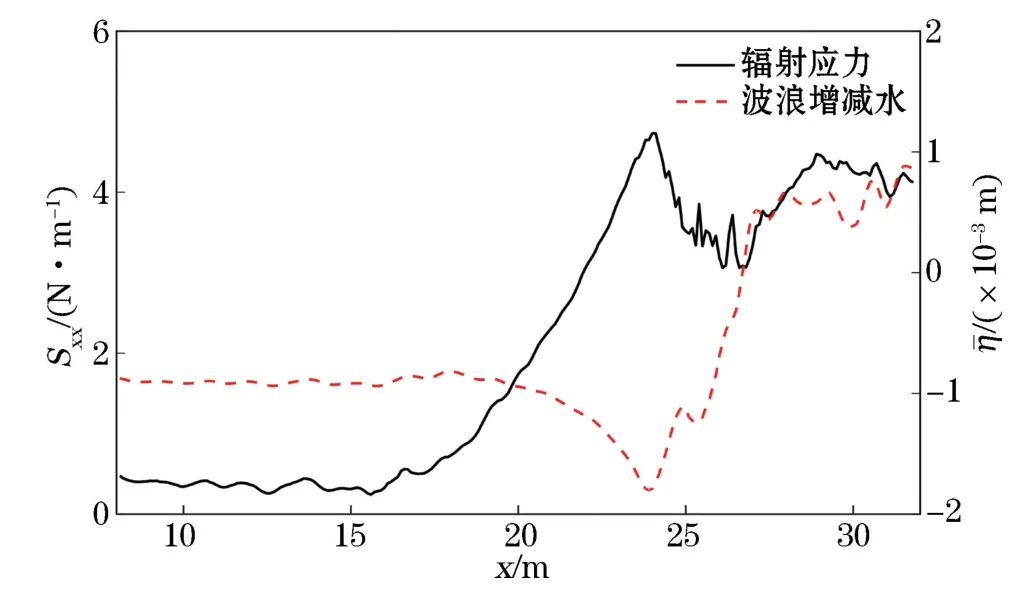
图6 CaseA波浪辐射应力与增减水沿程变化情况Fig.6 Variation of wave radiation stress and wave set-up,wave set-down under Case A

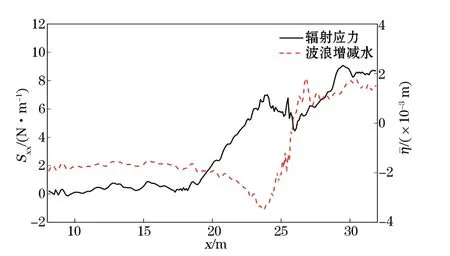
图7 CaseB波浪辐射应力与增减水沿程变化情况Fig.7 Variation of wave radiation stress and wave set-up,wave set-down under CaseB

另外,在堤前平底处,模型稳定后的辐射应力结果较小,这是由于随着波浪的传播,堤前反射波使波幅随着时间推移产生下沉现象,从而导致辐射应力定义公式中的速度积分项和动压积分项变小,最终导致了辐射应力结果偏低。由图8可见,Case A工况下15 m水槽处波面过程曲线及波幅偏移值随时间变化的曲线,将波幅偏移值量化为波浪上下幅值之和,并将其进行无量纲化,其中au表示波浪的上幅值,ad表示波浪的下幅值。波幅的偏移值在30 s后基本达到稳定状态,同时由图9可见数值水槽前端平底15 m处不同周期内的波幅偏移值与其对应的辐射应力值关系,较明显地反映出潜堤工况下的平底水槽部分辐射应力结果与对应周期内波浪幅值的偏移值成正相关,且受波幅变动影响较为敏感,波幅偏移值越小,辐射应力值越低。结合图8和图9来看,图8中当波浪波幅偏移值达到稳定状态时,其值对应于图9中辐射应力值大概为0.5 N/m处的点,较理论预估值低,而波浪传播初期的波浪偏移值对应的同周期内的辐射应力结果约为3 N/m,这与理论预估值基本一致,由此可见平底水槽处波浪稳定时辐射应力结果偏低是波幅偏移值变小造成的。而造成波浪波幅产生振荡的原因还需进一步地分析探讨。

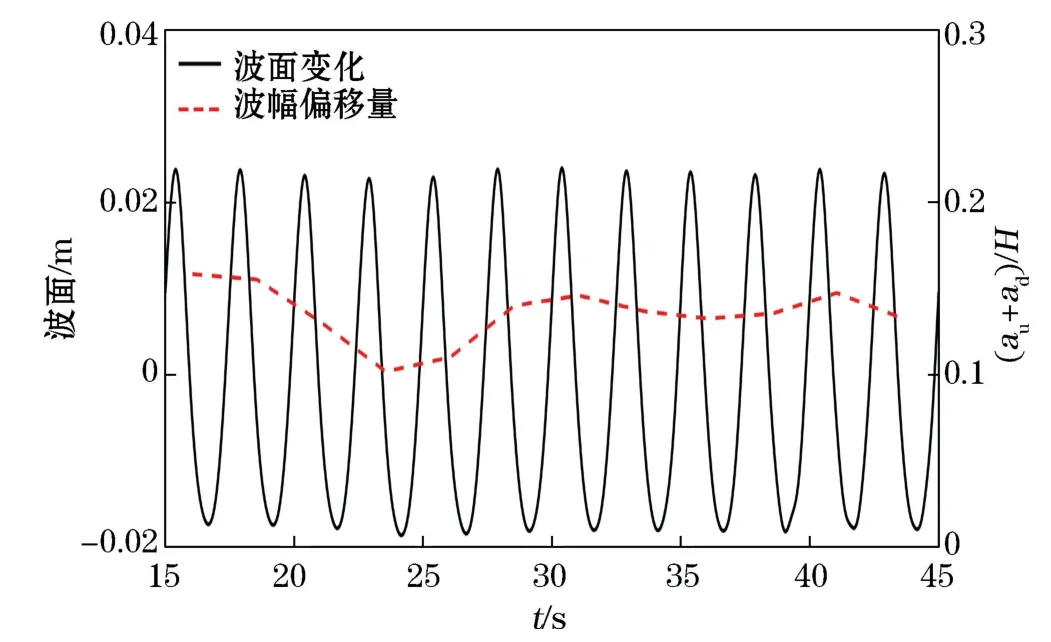
图8 CaseA工况中水槽15 m处波面变化及波幅偏移量变化Fig.8 Wave surface change and amplitude offset change at 15 m on the tank under Case A

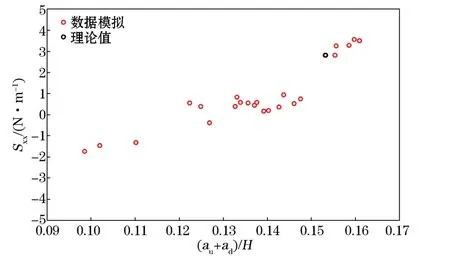
图9 CaseA工况水槽15 m处不同周期内波浪波幅偏移量与其对应辐射应力值关系Fig.9 The relation figure between wave amplitude offset and corresponding value of radiation stress at 15 m of tank under CaseA

4 结 语

本文应用Open FOAM数值模型模拟有破碎情况下潜堤地形的波浪传播,详细地输出了碎浪区波浪运动的流场信息,完整地计算了波浪在堤前平底、堤身及堤后平底处整个沿程的辐射应力和波浪增减水变化,并探究了堤前平底处辐射应力值受波幅偏移值的影响。

结果表明,数值模拟波浪在平底水槽中传播的波形及辐射应力结果与解析结果吻合较好;在含潜堤地形的水槽中,得到了与实验结果相吻合的破波区波面对比图,并计算输出了整个水槽内包括碎浪带及堤后平底水槽处的波浪辐射应力变化,发现波浪完全破碎后堤后坡面及平底处辐射应力呈先增大后趋于平稳的趋势,且堤后平底处较堤前平底处辐射应力值更大。

辐射应力结果与波浪增减水变化趋势在碎浪带内也能较好地对应波浪增减水方程;并且由于波浪反射造成的波幅的上浮与下沉,会间接导致辐射应力结果的增大与减小,且辐射应力值受波幅偏移值影响较为敏感。