海平面上升对中国沿海地区极值水位重现期的影响
2021-02-01圆纪棋严左军成李直龙罗凤云
庄 圆纪棋严左军成李直龙罗凤云
(浙江海洋大学 海洋科学与技术学院,浙江 舟山316022)
极值水位是指若干年内才有可能出现的高水位或低水位[1]。极值水位在海岸工程、海上工程、防洪防潮工程中有着重要的作用,是决定海洋工程能否满足安全需求的重要参考依据。在港口等海洋工程建设中,需对正常条件(即作业条件)和极端条件(即恶劣环境条件)下的极值水位做出估计。观测资料的长短不同,所采用的极值水位估计方法也不同[2-5],我国《港口与航道水文规范》[6]指出,在拥有长期水位观测资料的情况下可采用极值分布法;在拥有数年水位观测资料时可采用同步差比法;当仅有短期水位资料时,则需先求出设计水位再加减一个由附近验潮站长期资料得出的常数从而得出校核水位。但是这些方法需要验潮站本身或者临近的验潮站具有完整的长期观测资料,该条件比较苛刻通常难以满足,因此很难利用这些方法估计极值水位。为了解决观测资料时间不够长的困难,Pugh和Vassie[7]提出了用联合概率的方法计算极值水位,仅用短期实测数据便能求出极值水位,基于此,我国的方国洪等[1]对联合概率法进行改进,提出了条件分布联合概率法计算极值水位。但联合概率方法和条件分布联合概率方法在计算极值水位时都忽略了海平面长期变化对极值水位的影响。Marcos和Rohmer[8]研究表明,随着海平面上升,百年一遇的极值水位至少会缩短至50 a一遇。此外,研究表明,较长时间段内(比如50 a或者100 a)平均水位的长期变化也会对该时间段内的极值水位有一定的贡献[9-11]。因此在估计50 a一遇或者100 a一遇的极值水位时应当考虑海平面的变化以及平均水位的长期变化。
由温室效应产生的全球气候变暖将引起海平面上升,对沿海国家和地区居民、财产及生态系统的安全造成巨大的威胁。IPCC(Intergovernmental Panel on Climate Change)第五次气候评估报告中用典型浓度路径(Representative Concentration Pathway,RCP)来代表不同浓度的温室气体排放情景,按由低至高分别为RCP2.6、RCP4.5、RCP6.0和RCP8.5的四种情景,分别对不同情景下的海平面上升做出了预测[12-14]。
基于我国沿海10个验潮站资料,将利用皮尔森Ⅲ型(P-Ⅲ)模型探讨不同RCP情景下海平面上升对我国沿海地区极值水位重现期的影响,以期为我国沿海地区未来的海岸工程建设和防洪、防潮等海洋工程的建设提供参考,以更好地应对全球气候变化。
1 研究区域与数据来源
为了更准确地计算中国沿海的极值水位重现期的变化,本文选取了葫芦岛、秦皇岛、青岛、连云港、长涂、坎门、厦门、汕尾、北海及东方共10个验潮站的资料,各验潮站较为均匀地分布于我国渤海、黄海、东海和南海四个海区(图1),各站点数据的时间间隔均为1 h,但数据的时间范围及各验潮站所代表的潮汐类型各有不同(表1)。本文选取的站点具有较好的代表性,如汕尾站是南海受陆架影响较大的代表站点,东方站则是南海开阔海区的代表站点,北海站是北部湾沿岸的代表站点,厦门站则是台湾海峡的代表站点。此外,Santamaria和Vafeidis[15]指出不同的潮汐类型会对极值水位产生不同的影响,因此各验潮站的潮汐类型也涵盖了规则半日潮、规则全日潮、不规则半日潮和混合全日四种类型。

图1 中国沿海地区10个验潮站的位置Fig.1 Locations of the 10 tide gauge stations along the coast of China

表1 10个验潮站数据年份与潮汐类型Table 1 Data period and tidal type of the 10 tidal stations
采用的海平面上升数据是基于CMIP5(Coupled Model Inter-comparison Project Phase 5)并结合温室气体排放得到的。4种RCP情景(RCP2.6,RCP4.5,RCP6.0和RCP8.5)下2050年和2100年的未来海平面上升值如表2所示[12-14]。

表2 不同RCP情景下海平面的上升值[12-14]Table 2 Sea level rise under different RCP scenarios cm
2 研究方法
为研究不同RCP情景下海平面上升对中国沿海地区极值水位重现期的影响,首先需要得到RCP情景下的极值水位,其次再利用皮尔森Ⅲ型(P-Ⅲ)模型对极值水位重现期进行预测。RCP情景下的极值水位(Scenario Extreme Water Level,SEWL)被定义为未来海平面上升(Sea Level Rise,SLR)与当前极值水位(Current Extreme Water Level,CEWL)的结合。
2.1 天文高潮的计算方法
本文将潮汐采用调和分潮表示式:
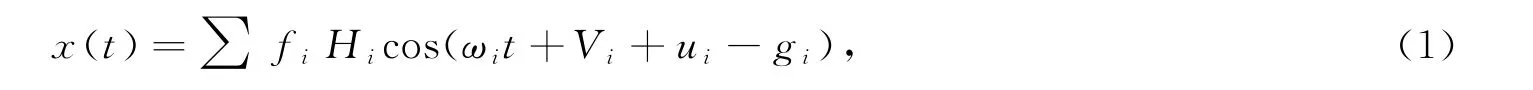
式中,t为时间,f为交点因子,i代表分潮,H和g为调和常数即振幅和迟角,ω为分潮角速度,V为分潮初相角,u为相角的交点订正。
验潮站的实际潮位由天文潮位和非天文潮水位两部分组成,非天文潮水位主要是风暴引起风暴增水。本文参考方国洪等[1]提出的天文潮位与非天文潮位分离方法将实际潮位分离得到天文潮和风暴增水两部分。首先对验潮站的资料逐年进行调和分析求出该验潮站各年的潮汐调和常数,再利用各年的潮汐调和常数对应后报各年的天文潮位,最后将后报的天文潮组成一个长时间序列并取最大值即为天文高潮,将验潮站的实际潮位减去天文潮位即可得风暴增水的值。例如,葫芦岛潮位数据的时间范围为1960—1986年,该潮位由天文潮和非天文潮位组成,要得到葫芦岛1960—1986年的天文潮的做法是:先对1960年的数据进行调和分析,得到1960年的潮汐调和常数,再后报出1960年的天文潮;依次类推,分别得到1961年和1962年直到1986年的每年的天文潮,最后将每年的天文潮按时间先后排列得到1960—1986年的天文潮。之所以用每年分析所得潮汐调和常数后报当年潮汐,而不用多年平均潮汐调和常数后报,是因为实际上各年分析所得潮汐调和常数有一定变化,用当年分析结果后报有利于更好消除潮汐部分的影响[1]。
2.2 风暴增水累积概率分布
从每个验潮站的观测时间序列数据中减去天文潮位便可得到风暴增水。每年的风暴增水年最大值构成一个风暴增水极值序列,利用该序列在P-Ⅲ模型的基础上拟合概率分布函数,依次得到所有观测站的风暴增水极值曲线。
f(x)是P-Ⅲ的概率密度函数:

式中,Γ(α)为Gamma函数;x为风暴增水值;α,β和α0为形状、尺度和位置参数其中,为风暴增水的平均值,Cv和Cs分别为分散系数和偏态系数,Cv=为验潮站数据时间序列的长度;Cs/Cv的值在每个站都是恒定的。
极值水位发生的概率p的计算公式为

式中,x p为在特定的p下的风暴增水极值,F(x)为风暴增水的累积概率分布函数。
2.3 CEWL和SEWL的累积概率分布
当前极值水位(CEWL,g p)指风暴增水极值与天文高潮相叠加的水位,计算方法为
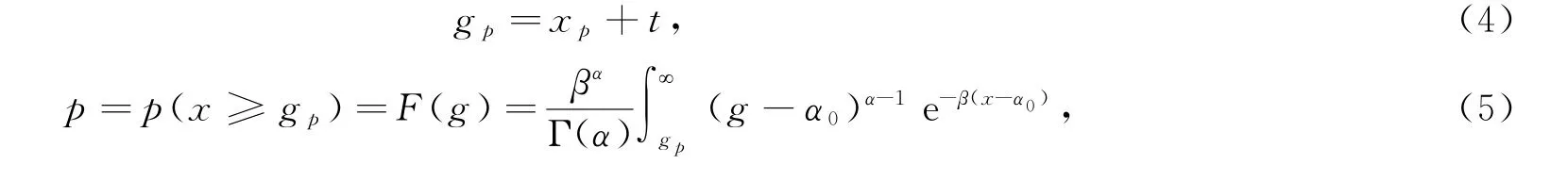
式中,t为天文高潮的高度,F(g)为CEWL的累积概率分布函数。
气候变化和海平面上升对风暴潮的强度和发生频率都可能产生影响,但是这种影响目前很难定量化,因此在一些气候变化背景下的风暴潮相关研究中,通常假设风暴潮强度和发生频率在统计上是不变的[17-19]。本文采取类似的做法,我们认为在各RCP情景下,风暴潮的强度和发生的频率是不变的,即不考虑气候变化和海平面上升对风暴潮强度和发生频率的影响。因此,RCP情景下的极值水位(SEWL,h p)可以认为是当前极值水位和不同RCP情景海平面上升高度的线性叠加,即:

式中,r为海平面上升的高度,F(h)为SEWL的累积概率分布函数。
2.4 极值水位重现期的计算方法
通常来说,极值水位的重现期是沿海风险评估与国防决策的重要指标。计算极值水位的重现期T公式为:T=1/p。
3 结 果
3.1 各验潮站的天文高潮
利用调和分析法对所搜集的验潮站资料进行处理,计算出本研究选取的10个验潮站的天文高潮值,如图2所示。结果表明:10个站的天文高潮值为94~326 cm,平均值为232 cm。其中厦门站的天文高潮值最大,为326 cm;秦皇岛站的天文高潮值最小,为94 cm。不同验潮站所处海区的地形差异是引起天文潮高度差异的重要原因。
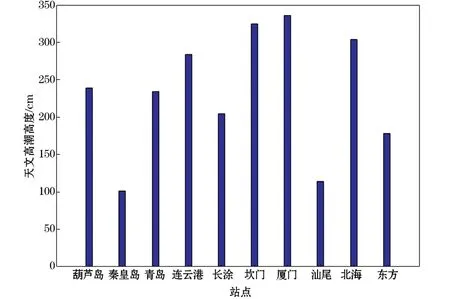
图2 10个验潮站的天文高潮高度Fig.2 High tidal heights recorded at the 10 tide gauge stations
3.2 风暴增水的累计概率分布
将长期观测记录的水位数据减去调和分析得到的天文潮数据后得到的风暴增水数据拟合到P-Ⅲ模型,可得风暴增水的累计概率分布曲线,如图3所示。由图3可知,当p=0.01%时,连云港站的风暴增水极值最大,为313 cm;坎门站次之,为295 cm;东方站最小,为192 cm。当p=99.9%时,连云港站的风暴增水极值最大,为90 cm;厦门站次之,为79 cm;东方站最小,为41 cm。这表明本研究中使用的站点之间的累积概率分布曲线存在明显差异。利用图3的数据,我们可以求得极端风暴增水的重现期,如表3所示。
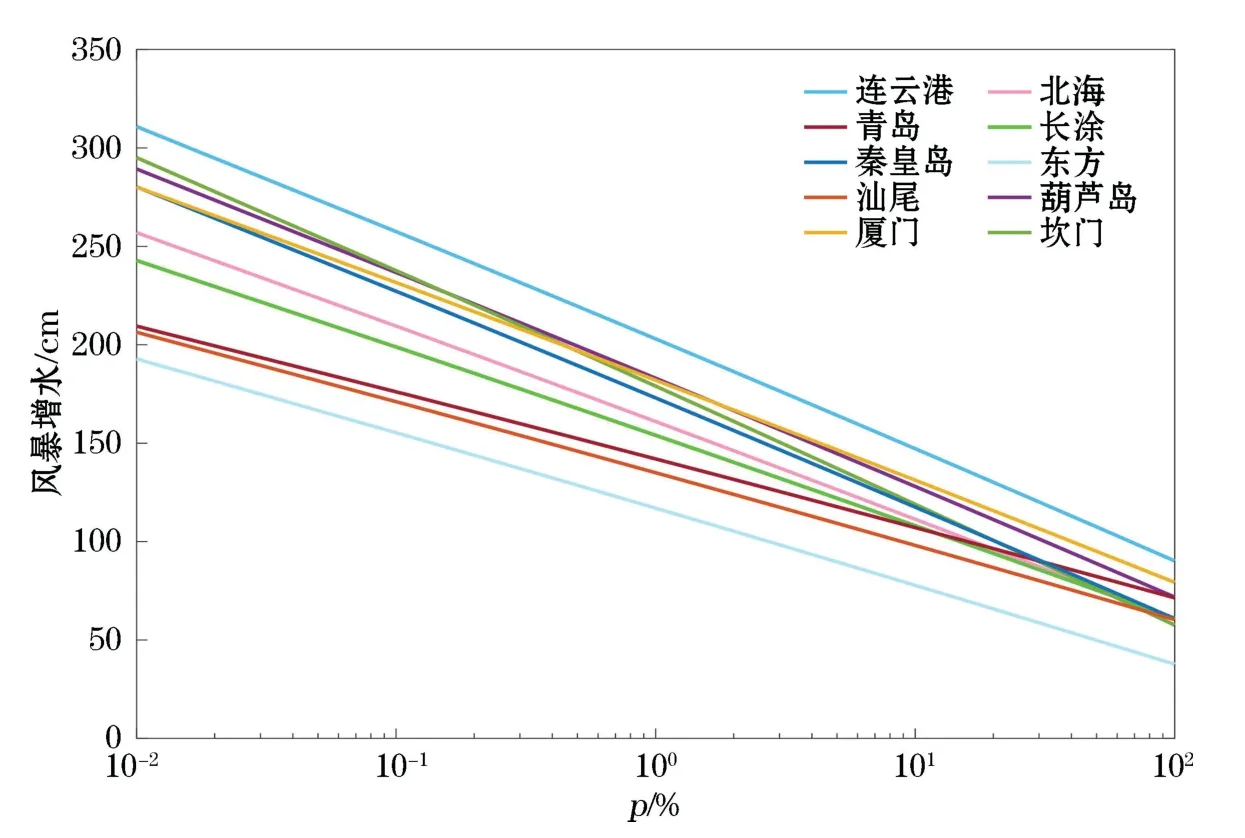
图3 验潮站记录的风暴增水累积概率分布曲线Fig.3 Cumulative probability distribution curves for the storm surges recorded at the 10 tide gauge stations
Katherine等[20]指出,沿海水位是由确定性(如天文潮)和随机性过程(如波浪、风暴潮和海平面异常)共同驱动产生的。每个过程对水位的贡献取决于气候和地质的区域差异,以及海滩形态、海岸方向和大陆架水深的局部尺度变化。中国沿海海岸线较长,所研究的10个验潮站的地理环境有差异,受到不同的水文与气象环境因素影响,故各个验潮站的风暴增水极值不同。由表3可以看出,当风暴增水极值重现期为100 a时,本研究中的风暴增水116~202 cm,其中连云港站百年一遇的风暴增水极值最大,为202 cm;东方站的最小,为98 cm。

表3 代表性重现期的风暴增水极值Table 3 Storm surge extreme values corresponding to representative recurrence periods cm
3.3 研究站位的CEWL和SEWL累积概率分布
将每个验潮站的风暴增水的最大值分别与其天文高潮相结合,叠加的高度数据拟合到P-Ⅲ模型,可以得到当前极值水位的累计概率分布曲线,如图4所示。由图4可知,所有验潮站的当前极值水位累计概率分布曲线和风暴增水累计概率分布曲线相比均增加。当p=0.01%时,坎门站的当前极值水位的极值最大,为626 cm;厦门站次之,为625 cm;汕尾站最小,为324 cm。当p=99.9%时,厦门站的当前极值水位的极值最大,为425 cm;坎门站次之,为383 cm;秦皇岛站最小,为160 cm。

图4 10个潮汐站的CEWL累积概率分布曲线Fig.4 Cumulative probability distribution curves for the CEWLs at the 10 tide gauge stations
将不同RCP情景下的海平面上升高度值叠加到当前极值水位,叠加的高度数据拟合到P-Ⅲ模型,可得到不同RCP情景下极值水位发生的概率。以汕尾站和坎门站为例,分析2个站在4个RCP情景下(每个RCP中最低值、平均值和最高值三个级别)2050年和2100年极值水位发生的概率以说明海平面上升对极值水位的影响,结果如图5所示。为了体现海平面上升对极值水位重现期的影响,当前极值水位累计频率概率曲线也包括在图5中。由图5可知:海平面上升导致相同概率下RCP情景下的极值水位显著高于当前极值水位;4种RCP情景相比,相同概率下RCP8.5的极值水位最高,RCP4.5和RCP6.0次之,RCP2.6情景下的极值水位最低;相同概率下2100年的RCP情景下极值水位显著高于2050年的RCP情景下极值水位。
利用单一的RCP情景下极值水位发生的概率可以估算出其极值水位与其相应的重现期。以汕尾站为例:RCP4.5情景下,2050年的极值水位为210~350 cm,到2100年极值水位增加为240~390 cm。同样,在RCP8.5情景下,2050年的极值水位为220~360 cm,2100年极值水位增加到240~410 cm。
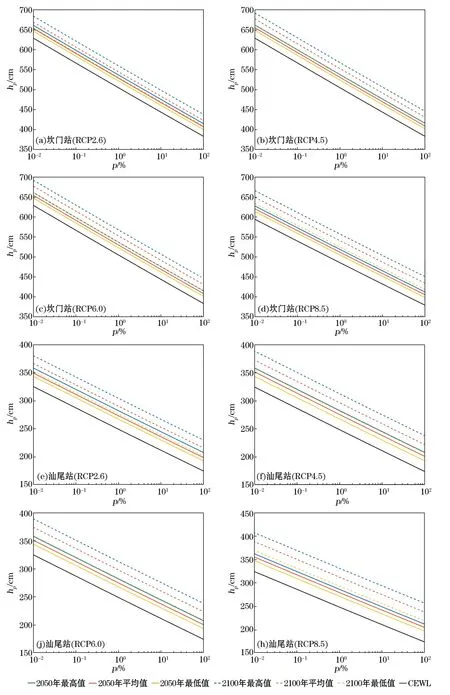
图5 4个RCP情景下的坎门站和汕尾站的SEWL频率曲线Fig.5 SEWLs for Shanwei and Kanmen Stations under the four RCP scenarios
3.4 海平面变化下重现期的变化
不同程度的海平面上升对极值水位的重现期影响也不一样。本文计算了从当前极值水位到RCP情景下极值水位重现期的变化,并且对比了相同极值水位下当前极值水位重现期与RCP情景下极值水位的变化,如表4所示。由表4可以看出,随着海平面的上升,RCP情景下极值水位的重现期相比于当前极值水位重现期会显著缩短,2100年的下降趋势比2050年更为显著。在RCP8.5(高水平)情景下,当前极值水位重现期为50 a的水位在2050年将变为8 a一次,到2100年将会变为1 a一次。同样,当前极值水位重现期为100 a的水位在2050年将变为17 a一次,到2100年将会变为2 a一次。对于当前极值水位重现期为1000 a的水位在2050年将变为172 a一次,到2100年将会变为25 a一次。此外,其他RCP情景下的不同3个级别的重现期变化也将显著缩短,这意味着随着海平面的上升,重现期较长的极值水位将更加频繁地发生。
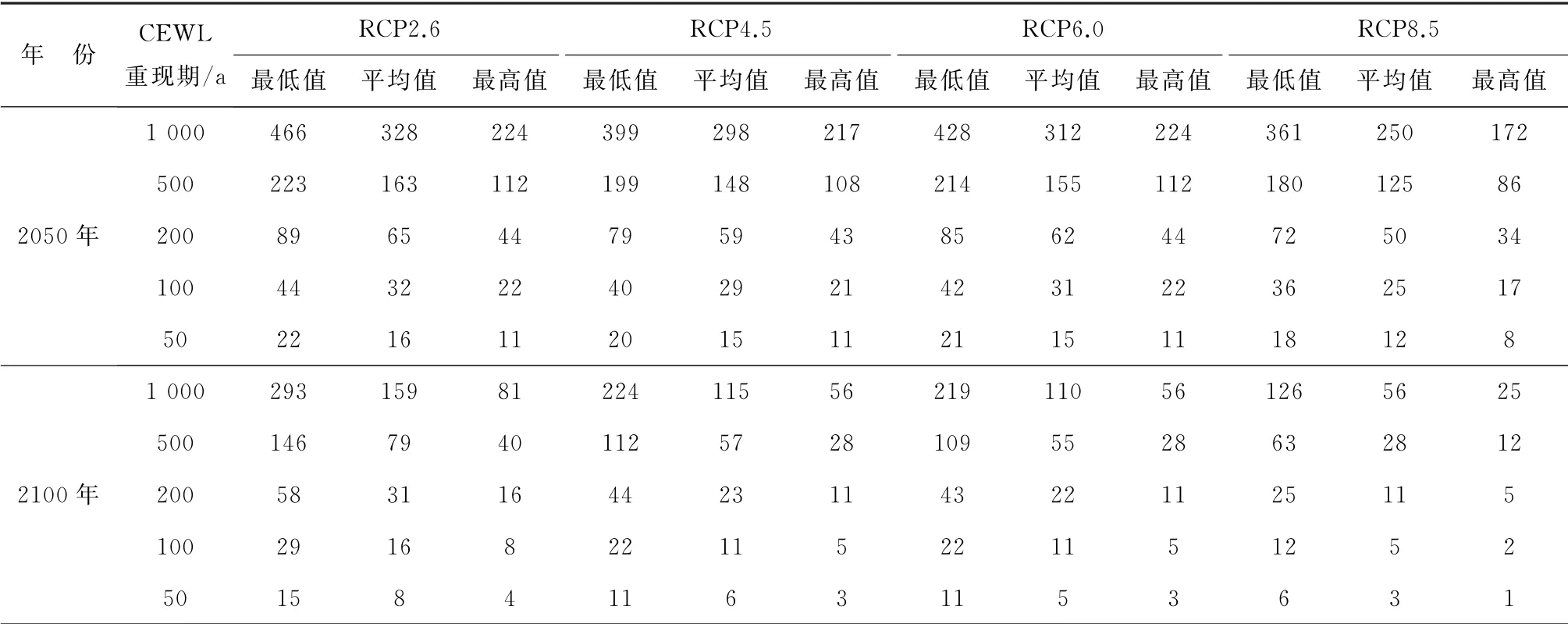
表4 SEWL的平均重现期Table 4 Averaged recurrence periods of the SEWLs a
4 结 论
将未来的海平面上升高度与当前极值水位相结合,通过P-Ⅲ模型重新计算极值水位,并计算其重现期,将当前极值水位的重现期与RCP情景下极值水位的重现期进行对比,分析海平面上升对极值水位重现期的影响。以中国沿海为例,研究结果表明:由于气候变化引起的海平面上升,极端水位的重现期明显缩短;具体来说,当前极值水位和RCP情景下极值水位在不同时间尺度的RCP情景和每个RCP情景中的水位之间的变化表明了海平面上升对极值水位的变化有显著的影响。重现期在RCP8.5情景下缩短最为显著;例如,对RCP8.5下的高水平的预测,即使是目前概率很低的当前极值水位千年一遇事件,在RCP8.5(高水平)情景下2050年将会变成172 a一遇;这表明由海平面上升导致的极值水位重现期的显著缩短将会使沿海地区的风险将显著增加。
本文计算极值水位的方法仍有一些可以改进的地方,在计算RCP情景下极值水位时使用的海平面上升数据为全球海平面上升高度数据,由于海平面上升的全球分布在空间上是不均匀的,在研究特定区域的极值水位重现期受海平面上升的影响时,使用特定海域的海平面上升数据能够得到更为精确的结果。
