PIV亚像素匹配精度及粒子大小和浓度的影响

李 超蒋暑民马洪余戴德君黄传江

(1.自然资源部 第一海洋研究所,山东 青岛266061;

2.青岛海洋科学与技术试点国家实验室 区域海洋动力学与数值模拟功能实验室,山东 青岛266237;3.自然资源部 海洋环境科学与数值模拟重点实验室,山东 青岛266061)

激光粒子图像测速技术(Particle Image Velocimetry,PIV)是采用高速CCD相机、激光器等设备对流场进行成像,再通过对相邻两幅流场图像加以互相关分析获取测量区域的流速和流向的方法[1]。相较于传统的单点测量方法,PIV技术具有多点同时测量、非接触测量、瞬时性和高分辨率等优点。因此,自20世纪80年代PIV技术被Adrian等学者提出以后迅速发展[2-5],并被应用在多个方面,如燃烧的火焰场、内燃机、微血管、飞机机翼复杂的外形流动以及火炮发射口流场测量等。

在应用PIV过程中,首先,需要向待测流场中均匀散播示踪粒子,这些粒子应具备如下特性:反光性良好、跟随性良好、不改变流体性质,各个示踪粒子之间互不影响等[6-8];然后,利用脉冲激光或连续激光片光源照亮待测量的流场区域,高速CCD相机摄取激光面上的粒子分布,在极短的时间内记录粒子图像帧序列;最后,选定合适的窗口针对粒子图像序列进行互相关分析和亚像素算法分析,计算得出2帧图像中相对应的粒子位移的大小和方向,从而获得测量区域的瞬时速度场[9-10]。在这个过程中,图像匹配是整个测量过程中的关键技术之一,示踪粒子直径的大小和粒子的浓度对整个测量结果也起着至关重要的作用[11]。

相邻图像的相关分析或图像匹配是PIV技术获取流场信息的关键,对原始图像的相关分析[12-13]通常分为2步:1)通过相关搜索匹配获得整像素位移,2)在整像素位移基础上进行亚像素的位移匹配。整像素位移很容易获得,但在实际流场中,所选匹配区域的位移值一般不会恰好为像素的整数倍,所以整像素的位移精度在实际应用中远远不够[14]。为了提高PIV的测量精度,通常采取3种方法:1)提高高速CCD相机的分辨率,但是由于当前相机技术限制,CCD相机的分辨率有限,很多时候并不能满足需求;2)提高摄像系统的放大倍数,但放大倍数的增加意味着可测量面积的减小;3)采用亚像素位移匹配算法,亚像素位移算法在高精度PIV测量中具有重要的意义[15-16]。

本文比较了二次多项式曲面拟合法和基于梯度的亚像素位移匹配算法,给出2种算法的匹配精度和各自的特点,并进一步评估了匹配窗口的大小、示踪粒子的直径和粒子的浓度对测量精度的影响。相关结果对于合理使用PIV技术开展实验和测量结果误差分析具有一定的参考价值。

1 数据与方法

1.1 计算机仿真粒子图像

为了比较不同的亚像素定位算法精度且找到合适的粒子大小和粒子浓度,必须采用能够精确控制位移的粒子图像。本文采用Zhou和Goodson[17]提出的算法,利用计算机产生随机分布的高斯光斑来模拟粒子的分布,并精确控制粒子的移动距离。仿真粒子图像的生成函数可表示为

式中:x,y为仿真粒子图像每个像素灰度值所对应的位置;I1,I2分别是原始仿真粒子图像和精确移动后的仿真粒子图像灰度值;△u,△v为原始图像仿真粒子移动的位移分量;s为仿真粒子的数目;I0为仿真粒子的中心光强;x k,y k为仿真粒子在原始图像中的中心位置;a为仿真粒子的直径。

利用式(1)、式(2)生成2幅仿真粒子图像,如图1所示:其中,仿真粒子图像大小为128像素×128像素;仿真粒子数目为300个,中心光强为255,直径为4个像素。图1a为原始仿真粒子图像,图1b是在图1a基础上所有粒子向右移动1.5个像素后的仿真图像,即△u=1.5且△v=0的情况。

图1 仿真粒子图像Fig.1 Particle images simulated by computer

1.2 亚像素位移匹配算法

1.2.1 互相关匹配算法获取整像素位移

亚像素位移的获取首先通过互相关匹配获得整像素位移,然后再基于整像素匹配结果进行亚像素匹配。互相关匹配需要2幅粒子图像,在前一时刻粒子图像中选取匹配窗口f(x,y),在后一时刻粒子图像中选取同样大小的匹配窗口g(i,j)进行匹配,其中相关系数最大的窗口位置即可视为2帧照片的整像素位移量。本文整像素位移的获取采用Willert和Gharib[18]在1991年提出的相关函数:

式中,R(i,j)为相关系数;(x,y)为前一时刻匹配窗口内灰度值对应位置坐标;i,j为后一时刻匹配窗口相对于前一时刻窗口的整像素移动位置,一般选择窗口大小为32像素×32像素或64像素×64像素;通过上述相关函数获取整像素位移之后,需要进一步通过亚像素位移匹配算法来提高测量精度。本文比较了曲面拟合法和基于梯度的亚像素位移算法。

1.2.2 曲面拟合法

实际计算中常用的曲面拟合法为二次多项式曲面拟合,拟合的参量为获取整像素位移时计算得到的相关系数。二次多项式曲面拟合法需要先选定拟合窗口,通常选取拟合窗口为3×3,即根据整像素位移结果及其周围相近8个点的相关系数组成3×3的相关系数矩阵,利用二次多项式拟合为连续曲面,找出此曲面的极值点所对应的位置即为最佳匹配结果。

二次多项式的解析方程为

式中,C为曲面拟合相关系数,(x,y)为以整像素位移匹配结果为中心点建立坐标系中的坐标点,用最小二乘法求解待定系数k i,进而可求得极大值点,该极大值点对应位置即曲面拟合法获得的亚像素精度的位移值。

1.2.3 基于梯度的亚像素位移算法

鉴于在PIV测量过程中,粒子位移量不大,假设位移前后同一点的灰度值相同,则:

式中,f(x,y)和g(x,y)分别为前一时刻和后一时刻所对应的匹配窗口内的灰度值;△x,△y为整像素位移值;x0和y0为亚像素位移值。将式(5)进行一阶泰勒展开并舍去高阶小量,可得:

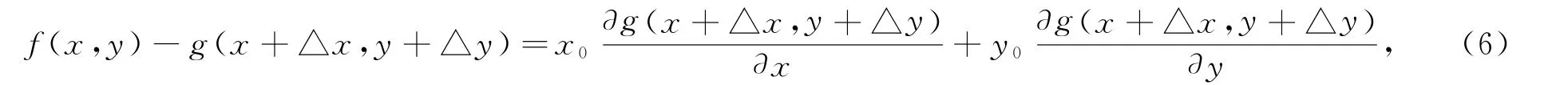
假设匹配窗口m×m内各个像素点的位移都相等,就有m×m个式(6),再利用最小二乘法可以推导出:

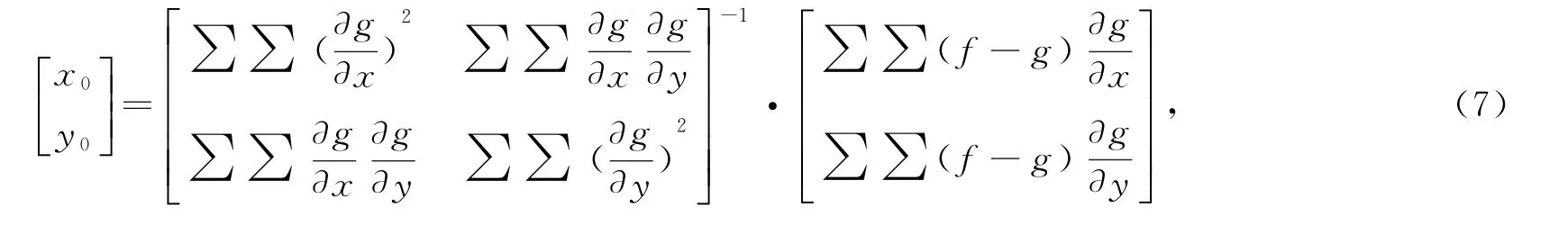
求得亚像素位移值x0和y0并结合整像素位移即可获得精度较高的位移值。

2 结果与分析

2.1 曲面拟合法与基于梯度亚像素位移算法精度对比

前文介绍了曲面拟合法和基于梯度亚像素位移算法,下面将对这2种亚像素算法的匹配精度和特征进行对比。首先针对粒子均匀移动的理想情况进行分析,所谓均匀移动指的是图像中的所有粒子移动大小和方向完全一致。利用的仿真粒子图像大小为128像素×128像素,仿真粒子数目为1000个,仿真粒子直径为3个像素。图像互相关匹配时的匹配窗口大小为32像素×32像素。图像互相关匹配前进行简单的滤波,并不会影响仿真粒子的直径大小。图2给出了二次多项式曲面拟合法与基于梯度亚像素位移算法的匹配精度及特征。

图2 二次多项式曲面拟合法与基于梯度亚像素位移算法得到的亚像素匹配结果及误差对比Fig.2 Subpixel displacements and errors by using quadratic polynomial surface fitting and subpixel displacement algorithm based on gray gradient

图2a和图2b为使用二次多项式曲面拟合法得到的结果,图2c和图2d为使用基于梯度的亚像素位移算法得到的结果。针对选定的真实位移量,通过选取不同的图像对和在前一时刻图像中选取不同窗口位置,在下一时刻图像中进行匹配,获得多个匹配结果,进而进行误差分析。图2为针对每个选定的真实位移量,100次匹配实验结果:二次多项式曲面拟合法整像素位移时的误差较小,约为0.02个像素,而在非整像素位移时误差比较大(图2a),且平均误差值随着粒子真实位移的改变呈现出周期性的变化(图2b),但均在0.08个像素内;基于梯度亚像素位移算法在整像素时的误差为0,所有误差也在0.08个像素左右(图2c,图2d)。

多次匹配实验结果的平均绝对误差分析(表1)可以看出:二次多项式曲面拟合法和基于梯度亚像素位移算法在相同匹配窗口时x方向和y方向的匹配精度差别不大。二次多项式曲面拟合法的计算精度随匹配窗口的增大而提高,基于梯度亚像素位移算法在不同匹配窗口下的平均绝对误差大致相同。在匹配窗口为16像素×16像素时,基于梯度亚像素位移算法的匹配精度要优于二次多项式曲面拟合法的匹配精度;匹配窗口为32像素×32像素时,2种算法的匹配精度大致相同;匹配窗口为64像素×64像素时,二次多项式曲面拟合法要优于基于梯度亚像素位移算法。

表1 不同窗口大小下两种亚像素匹配平均绝对误差比较Table 1 Mean absolute errors of subpixel displacements by using quadratic polynomial surface fitting and subpixel displacement algorithm based on gray gradient for different window sizes

2.2 粒子浓度对测量结果的影响

在PIV测量流体过程中需要向流体中撒播示踪粒子,粒子浓度对PIV的测量精度有着十分重要的影响。利用准确控制仿真粒子图像的位移和不断改变生成粒子的数目,可以找到合适的粒子浓度范围,对实际实验过程中的PIV测量有一定的指导意义。图3给出了采用二次多项式曲面拟合法时不同粒子浓度对匹配精度的影响,采用的仿真粒子图像大小为128像素×128像素,仿真粒子直径为3个像素,仿真粒子真实位移为向右和向上分别移动1.5个像素。选择合适的匹配窗口大小,通过选取不同的图像对和在前一时刻图像中选取不同窗口位置,在下一时刻图像中进行匹配,获得100个匹配结果,进而统计得到误差分析结果。

图3给出了匹配窗口为16像素×16像素时,匹配误差随仿真粒子浓度的变化,这里粒子浓度指仿真粒子个数与仿真粒子图像总像素值的比值。从图中可以看出:匹配窗口为16像素×16像素时,粒子浓度0.04～0.36最为合适。改变匹配窗口大小后,最合适的仿真粒子浓度区间也发生改变,匹配窗口为32像素×32像素时,最合适的粒子浓度区间为0.008～0.440,匹配窗口为64像素×64像素时,最合适的粒子浓度区间为0.002～0.530。也就是说,匹配窗口越大,其包含的灰度值信息越多,最合适的粒子浓度范围也越大,建议在实际实验时,同时考虑所研究科学问题对流场空间分辨率的要求(匹配窗口的大小)和实验经济性,选择合适的粒子浓度。

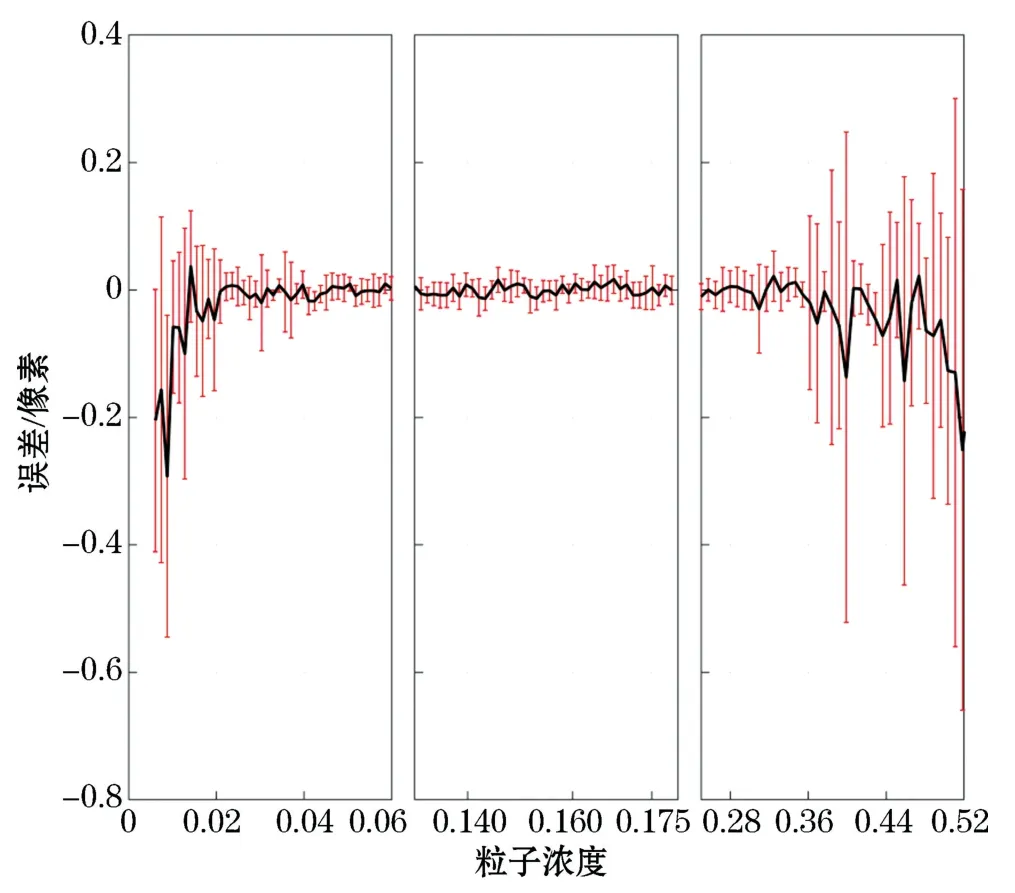
图3 亚像素匹配误差随仿真粒子浓度变化图(16像素×16像素)Fig.3 Variation of subpixel displacement errors with particle concentration(16 pixels×16 pixels)

需要说明的是,这里所指的粒子浓度是仿真粒子个数与仿真粒子图像总像素值的比值。在利用计算机生成仿真图像时,设置了避免粒子重合的算法,但也只是保证仿真粒子中心位置不会重合,导致在生成的仿真图像中,会不可避免的产生粒子边缘重合现象。因而本文给出的结果对于实验中所需的最低粒子浓度具有一定的指导意义。

2.3 粒子直径对测量结果的影响

PIV是一种非接触式测量技术,粒子的选择对测量结果有比较大的影响,首先粒子的密度必须与所测量流体的密度接近,这样选取的示踪粒子才能具有较好的跟随性,能很好地反映流场信息,粒子直径大小对测量精度也有很大的影响。我们利用精确控制仿真粒子的大小并采用二次多项式曲面拟合法来分析测量误差的变化,进而确定适合的粒子大小。仿真粒子图像大小为128像素×128像素,仿真粒子的数目为1000个,对应的粒子浓度为0.061,仿真粒子位移为向右和向上分别移动1.5个像素。通过选取不同的图像对和在前一时刻图像中选取不同窗口位置,在下一时刻图像中进行匹配,获得100个匹配结果,进而统计得到误差。

图4给出了不同匹配窗口下不同粒子直径时的误差大小。在匹配窗口为16像素×16像素时,粒子直径为2个像素和3个像素时误差较小,其中粒子直径为3个像素时误差最小。当匹配窗口为32像素×32像素时,粒子直径合适的范围为3～5个像素,在粒子直径为3个像素时误差最小,其误差值在0.02个像素内。当匹配窗口变为64像素×64像素时,粒子直径合适的范围为3～6个像素,粒子直径在5个像素时匹配精度最佳,其中粒子直径为3,4,5个像素时的误差值在0.02个像素内。总之,随着匹配窗口的增大,粒子直径合适的范围也在扩大。从整体来看,在这3种匹配窗口下,粒子直径为3个像素时的匹配误差均可接受。一般来讲,粒子直径越小,其跟随性越好,尤其是在测量湍流流场条件下,对粒子的跟随性的要求更高。

图4 不同匹配窗口下亚像素匹配误差随粒子直径变化图Fig.4 Variation of subpixel displacement errors with particle diameter for different window sizes

3 理想涡旋流场下的误差分析

前文在亚像素匹配精度分析时均采用粒子均匀移动的图像,匹配窗口内部位移相同,其运动方式较为简单,而在PIV的现实应用中很少会出现这种理想流动情况。因此,采用存在理想涡旋的粒子图像,分析其亚像素匹配误差更具有实际应用价值,下面对这种复杂的流场情况进行分析。仿真粒子图像大小为256像素×256像素,仿真粒子数目为3500个,对应的粒子浓度为0.053,仿真粒子直径为3个像素,仿真粒子的位移采用线性增加的方法,即距离旋涡中心越远,粒子的位移越大且方向垂直于旋涡中心指向该点的矢量。粒子图像互相关匹配时的匹配窗口大小为16像素×16像素,图5为二次多项式曲面拟合法与基于梯度亚像素位移算法得到的粒子影像及反演涡旋流场图,可以看出二者的差别不大,都能很好的表征涡旋的流场情况。

图6给出了使用二次多项式曲面拟合法和基于梯度亚像素位移算法得到误差分析结果,由图6可见:使用基于梯度亚像素位移算法得到的误差比使用二次多项式曲面拟合法得到的误差要小,使用二次多项式曲面拟合法的匹配误差基本稳定在0.2个像素以内,使用基于梯度亚像素位移算法得到的误差基本在0.05个像素以内。在粒子沿直线运动时,且匹配窗口为16像素×16像素情况下,基于梯度亚像素位移算法匹配精度高于二次多项式曲面拟合法。在复杂的流动状态下,匹配窗口内部存在粒子的相对位移时,基于梯度亚像素位移算法的匹配精度也明显优于二次多项式曲面拟合法。

图5 二次多项式曲面拟合法与基于梯度亚像素位移算法得到的涡旋流场Fig.5 Particle image and the vortex flow field obtained by using quadratic polynomial surface fitting and subpixel displacement algorithm based on gray gradient

图6 二次多项式曲面拟合法与基于梯度亚像素位移算法得到的误差对比Fig.6 Errors by using quadratic polynomial surface fitting and subpixel displacement algorithm based on gray gradient for the idealized vortex flow

4 PIV在水槽实验中的应用

2012年自然资源部第一海洋研究所建设了风-浪-流多功能实验水槽,水槽长45.0 m,宽1.0 m,高1.8 m,实验时水深一般设为1.2 m,为实现平稳出流,水槽两端各设增压腔一个。利用该水槽开展了波湍相互作用等实验研究。图7为风-浪-流多功能实验水槽玻璃段的示意图(玻璃段长32.4 m),造波机安装在水槽的首端,消波板安装在水槽尾部。在开展波-湍相互作用实验时,利用格栅振动产生湍流,采用PIV和ADV(Acoustic Doppler Velocimetry)测量水体速度,激光片光源平行于水槽,振动格栅位于测量区域的下方[20]。

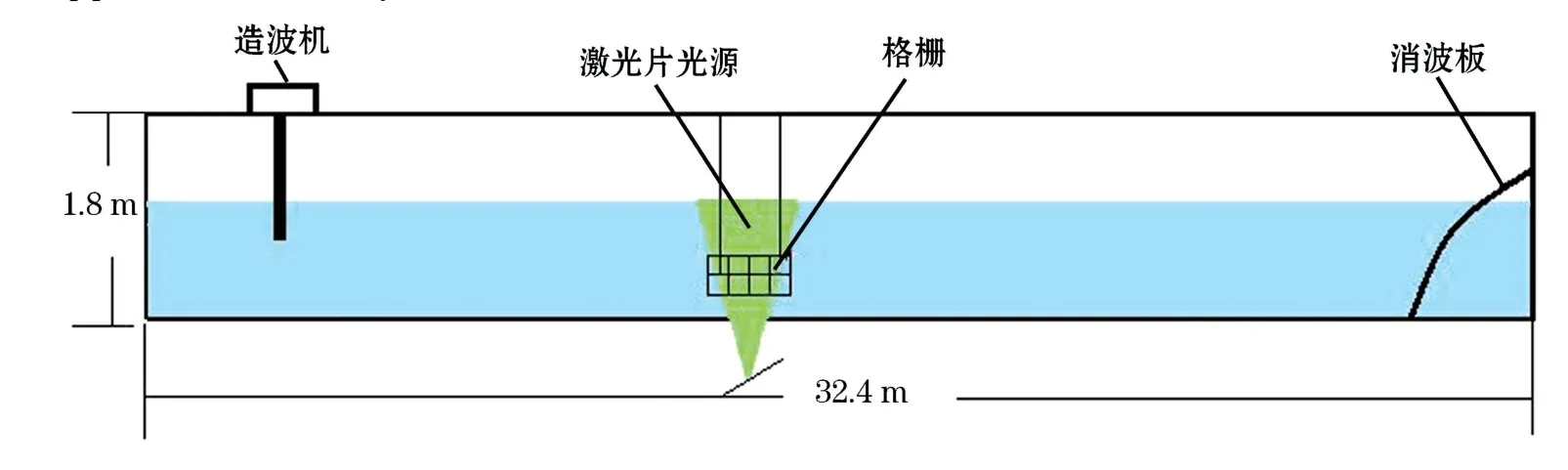
图7 风-浪-流多功能实验水槽玻璃段示意图Fig.7 Schematic diagram of wind-wave-flow multifunctional tank

图8给出的是格栅在水面以下26～31 cm处上下振动(频率为3 Hz,振幅为5 cm)时垂直采样得到的PIV影像。PIV测量时,以激光脉冲作为光源,采用高速CCD相机记录粒子图像,每两帧粒子图像之间的时间间隔为5 ms,采样频率为14.5 Hz,即每两对粒子图像之间时间间隔为0.069 s,粒子图像分辨率为1192像素×1600像素,对应的物理空间约为9.5 cm×12.8 cm,PIV影像的上端距水面约为4 cm。以其中一对粒子图像为例进行分析,对所选择的两帧粒子图像进行简单的滤波后识别出粒子直径的平均大小为2.96个像素,粒子直径不是整数,主要原因在于所用的示踪粒子在原始物理形态上就难以保证大小均匀,另外在利用图像识别粒子大小时,采用先识别每个粒子的面积,再假设每个粒子为圆形计算得出的粒子直径大小。PIV影像中粒子个数约为10600个,对应粒子浓度为0.0056。互相关匹配窗口选取64像素×64像素,利用二次多项式曲面拟合法和基于梯度亚像素位移算法进行亚像素匹配,结果如图8所示。2种算法反演得到的速度场除了个别点有差别之外,大部分区域都几乎一致。

图8 水槽格栅振动产生湍流实验PIV粒子影像及反演流场Fig.8 Particle image and the flow field of grid-generated turbulence in wave tank

我们选取了格栅振动试验中测得的200对连续的粒子图像,比较了2种算法所得速度场。图9给出了某一点(距水面14.720 cm,距测量区域左侧4.576 cm)2种亚像素算法所得速度的对比图,u为水平方向流速,v为垂直方向流速。互相关匹配窗口为64像素×64像素,两种亚像素算法所得流速变化趋势与量值基本一致,在使用合适的粒子大小和浓度时,2种亚像素算法均能得到较好的结果。

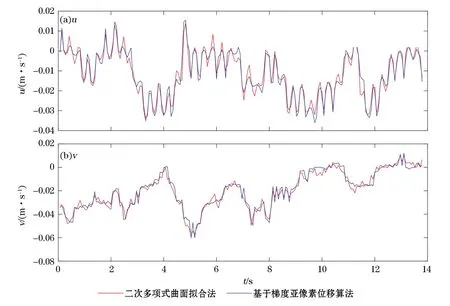
图9 二次多项式曲面拟合法与基于梯度亚像素位移算法得到的速度对比Fig.9 Comparisons of velocities obtained by using quadratic polynomial surface fitting and subpixel displacement algorithm based on gray gradient

5 结 论

本研究利用计算机仿真PIV粒子图像,通过精确控制粒子位移,讨论了不同匹配窗口下二次多项式曲面拟合法与基于梯度亚像素位移算法的匹配精度;进一步讨论了粒子浓度和直径大小对PIV测量结果的影响,给出了合适的粒子浓度范围和最佳的粒子直径大小;进而分析了理想旋涡流场下2种亚像素算法的误差,最后将2种算法应用到实际水槽实验PIV影像分析中。具体结论如下:

1)比较了二次多项式曲面拟合法与基于梯度亚像素位移算法2种方法,给出了不同窗口下二者的匹配精度。针对粒子均匀移动的理想情况,在相同匹配窗口时,x方向和y方向的匹配精度差别不大。二次多项式曲面拟合法匹配精度随着匹配窗口的增大而提高,基于梯度亚像素位移算法匹配精度几乎不随窗口变化,但两种亚像素算法的匹配精度均在0.1个像素内。

2)匹配窗口为16像素×16像素时,最合适的粒子浓度区间为0.040～0.360;匹配窗口为32像素×32像素时,最合适的粒子浓度区间为0.008～0.440;匹配窗口为64像素×64像素时,最合适的粒子浓度区间为0.002～0.530。匹配窗口越大,最合适的粒子浓度范围越大。在不同的匹配窗口下,粒子直径为3个像素时的误差均较小,为保证粒子跟随性,建议在PIV实际使用过程中,选择直径为3个像素的粒子为宜。

3)针对理想旋涡的粒子图像,利用基于梯度亚像素位移算法得到的误差比利用二次多项式曲面拟合法得到的误差要小,二次多项式曲面拟合法的匹配误差基本稳定在0.2个像素内,而基于梯度亚像素位移算法得到的误差基本在0.05个像素以内。