无穷维Hamilton算子谱理论研究综述

2021-02-01阿拉坦仓吴德玉

内蒙古师范大学学报(自然科学汉文版) 2021年1期

阿拉坦仓, 吴德玉

(1.内蒙古师范大学数学科学学院,内蒙古呼和浩特 010022; 2.内蒙古大学数学科学学院,内蒙古呼和浩特 010021)

0 引言

Hilbert空间中线性算子理论,尤其自伴算子谱理论是20世纪数学科学领域取得的最重要成果之一。有界自伴算子谱理论的奠基人D.Hilbert,在1904年至1910年完成的关于积分方程的六篇论文中阐述了有界自伴算子谱理论的思想。为研究量子力学问题,1927年至1929年J.von Neumann将有界自伴算子谱理论推广到了无界自伴算子领域。20世纪30年代,F.Riesz和M.S.Stone等人进一步完善了无界自伴算子谱理论框架。目前,自伴算子谱理论已经形成了比较完善的框架体系。众所周知的求解偏微分方程的分离变量法,又称Fourier级数法,就是以自伴算子谱理论为基础的。需要注意的是,当系统对应的算子是自伴算子时,该系统能量是守恒的,亦称封闭系统。然而,实际问题中也存在诸多能量不守恒的开放系统,其状态算子为非自伴算子。如散射理论和量子场理论领域的连续谱扰动问题以及量子力学中的特征值扰动问题,均属于非自伴算子谱理论范畴。因此,有必要研究非自伴算子的谱理论,拓广Fourier级数法的适用范围。目前,关于非自伴算子谱理论研究方法主要有预解算子方法、分块算子矩阵方法以及扰动理论等,虽然取得了一些重要突破,但还未形成完善的框架体系,非自伴算子谱理论是当代数学和力学领域亟待解决的重要理论问题之一。

如上所述,一般非自伴算子谱理论研究相对于自伴算子谱理论要复杂深刻。鉴于此,可以研究难度介于自伴算子和一般非自伴算子之间的算子。而这类算子就是无穷维Hamilton算子,它是由线性无穷维Hamilton 正则系统导出的具有深刻力学背景的分块算子矩阵。研究可知,利用自伴算子特征函数系的正交性,可以解决特征展开式中的系数计算问题,这是Sturm-Liouville问题及分离变量法的理论基础。一般非自伴算子的特征函数系不具有正交性,特征展开式中的系数计算问题至今是个难题。而无穷维Hamilton算子的特征函数系具有辛正交性,利用辛正交性可以解决特征展开式中的系数计算问题,这是钟万勰院士创立的弹性力学求解新体系[1]的理论基础。特征展开式的系数计算问题解决以后,面临的关键问题是特征展开式的收敛性问题,即特征函数系的完备性问题。该问题通过无穷维Hamilton算子的谱理论有望得到解决。因此,阿拉坦仓教授自1993年开始从偏微分方程的基本解转入研究无穷维Hamilton算子谱理论,这在国际上是起步较早的。

定义1设X是Hilbert空间,H:D(H)⊂X×X→X×X是线性算子,如果它具有分块形式

其中A、B、C是稠定闭线性算子且B=B*,C=C*,则称H为无穷维Hamilton算子。如果B,C均为自伴且非负算子,则称无穷维Hamilton算子H为非负Hamilton算子。

无穷维Hamilton算子的谱理论研究具有重要学术价值。无穷维Hamilton算子是介于自伴算子和一般非自伴算子之间的一类特殊的分块算子矩阵。关于无穷维Hamilton算子谱理论研究涉及Hilbert空间中线性算子理论、Krein空间中线性算子理论、辛空间中线性算子理论以及分块算子矩阵等诸多方面,具有很好的学术广度。此外,Sturm-Liouville问题是将Hilbert-Schmidt定理从有界自伴算子推广到了无界自伴算子的情形,然而无穷维Hamilton算子不仅将Hilbert-Schmidt定理从有界算子推广到了无界算子,还将自伴的情形推广到了非自伴的情形,具有很好的学术深度。

无穷维Hamilton算子的谱理论研究具有重要实际应用价值。钟万勰院士创立的弹性力学求解新体系,其理论基础是无穷维Hamilton算子特征函数系的完备性,而通过无穷维Hamilton算子的谱理论研究有望可以解决特征函数系的完备性问题。Hamilton矩阵谱对称问题是冯康院士课题组创立的辛几何算法[2]的理论基础,而通过无穷维Hamilton算子剩余谱分布,可以刻画无穷维Hamilton算子谱的对称问题。此外,吴文俊院士创立的吴方法[3]与Hamilton系统反问题之间联系紧密。

目前,研究无穷维Hamilton算子谱理论的学者很多,包括国外的Azizov[4]、Kurina[5-6]、Langer[7]以及Wyss[8]等,国内有以阿拉坦仓教授为带头人的无穷维Hamilton算子研究团队[9-12]、钟万勰[13-16]、周建方[17]等。随着无穷维Hamilton算子谱理论研究的深入,国内外核心期刊上发表的论文数量也大幅增加,如《中国科学:数学(中、英文版)》《数学学报(中、英文版)》《数学年刊》《数学物理学报》、AppliedMathematicalModelling、LinearAlgebraandItsAppliations、LinearandMultilinearAlgebra、IntegralEquationsandOperatorTheory、JournalofOperatorTheory、OperatorsandMatrices、MathematischeNachrichten等。鉴于此,本文对无穷维Hamilton算子谱理论研究团队及所取得的研究成果做一综述,其内容包括团队带头人及核心成员构成、无穷维Hamilton算子辛自伴性、无穷维Hamilton算子特征函数系的完备性以及无穷维Hamilton算子数值域等领域取得的成果。此外,本文还提出了关于无穷维Hamilton算子谱理论方面有待解决的问题。

1 无穷维Hamilton算子研究团队现状

无穷维Hamilton算子研究团队带头人是阿拉坦仓教授,现任内蒙古师范大学党委副书记、校长。他是第十三届全国政协委员,国家民委决策咨询委员会委员,曾获得内蒙古自治区青年科技标兵、内蒙古自治区青年科技奖、内蒙古自治区有突出贡献的中青年专家、内蒙古自治区自然科学二等奖和三等奖、宝钢优秀教师奖、内蒙古自治区教学名师、全国优秀科技工作者等荣誉和奖项,并入选内蒙古自治区新世纪“321人才工程”第一层次人选、内蒙古自治区高等教育人才培养“111工程”第二层次人选以及内蒙古自治区“草原英才”等人才工程。因为在无穷维Hamilton算子谱理论方面的奠基性工作,阿拉坦仓教授主持承担的成果项目“无穷维Hamilton算子及其应用”获得了2007年度内蒙古自治区自然科学三等奖。2008年阿拉坦仓教授创建了无穷维Hamilton系统研究中心,团队成员由他培养的博士和硕士组成。无穷维Hamilton系统研究中心的成立为无穷维Hamilton算子谱理论研究提供了重要平台,解决了无穷维Hamilton算子特征函数系的完备性问题以及谱的结构等重要问题,使得无穷维Hamilton算子谱理论研究取得重要进展。基于此,他主持承担的成果项目“无穷维Hamilton算子的谱结构及其完备性”获得了2011年度内蒙古自治区自然科学二等奖。2012年开始,阿拉坦仓教授提出了基于一般分块算子矩阵,利用数值域理论和本质谱理论,包括经典数值域、广义数值域、Fredholm性质、Weyl性质等,来研究无穷维Hamilton算子谱结构的建设性研究思路,取得了一系列具有开创性的成果,从而被评为全国优秀科技工作者。2018年,他带领的“数学教学科研蒙汉双语教师团队”入选教育部首批“全国高校黄大年式教师团队”。目前,无穷维Hamilton算子研究团队核心成员中有教授6人、博士研究生导师5人、硕士研究生导师6人,团队成员共主持国家自然科学基金18项,完成学术专著4部,完成教材2部,其中包括“十二五”规划蒙古文教材1部,完成学术论文300余篇,其中SCI检索100余篇。

2 无穷维Hamilton算子辛自共轭性

从一般的分块算子矩阵角度来说,无穷维Hamilton算子满足

(JH)*⊃JH,

(JH)*=JH,

则称无穷维Hamilton算子是辛自共轭(或称辛自伴)。无论研究无穷维Hamilton算子谱分布、谱扰动还是特征函数系的完备性问题,都离不开无穷维Hamilton算子的辛自共轭性。于是,运用扰动理论以及Schur分解给出如下结论:

(1) (JH)*=JH;

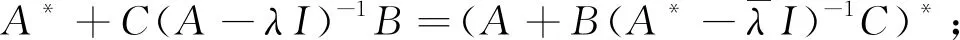
根据上述定理易得,当C关于A的相对界小于1且B关于A*的相对界不超过1,或者当C关于A的相对界不超过1且B关于A*的相对界小于1,则无穷维Hamilton算子是辛自共轭的。此时,自然可以提出的问题是: 两个相对界的乘积小于1能否保证其无穷维Hamilton算子的辛自共轭呢？答案是肯定的。

上述结果将无穷维Hamilton算子共轭算子的运算问题巧妙地转化成了Schur补的共轭以及线性算子相对界的计算问题,具有重要意义。类似地,还可以考虑斜对角占优的无穷维Hamilton算子。

3 无穷维Hamilton算子特征函数系的完备性

在Sturm-Liouville问题和Hilbert-Schmidt定理中利用自伴算子特征函数系的正交性解决了特征展开式系数计算问题。然而,无穷维Hamilton算子特征向量和广义特征向量具有辛正交性,故辛特征展开式的系数计算问题同样可以解决。于是,在Hamilton体系下采用分离变量法亟待解决的问题是展开式的收敛性问题,即完备性问题。由此可得如下结论,为弹性力学求解新体系提供了理论保障。

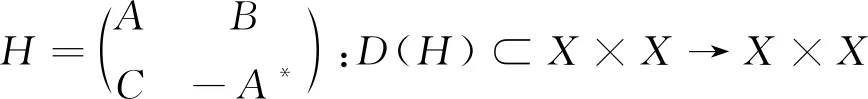
此外,还考虑了一类薄板问题对应的常系数偏微分方程

其边界条件为

将此微分方程导向Hamilton体系后,其对应的无穷维Hamilton算子为

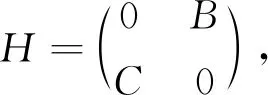
其中

得到如下结论:

上述结果解决了一些抽象无穷维Hamilton算子和具体问题对应的无穷维Hamilton算子特征函数系和广义特征向量组的完备性问题,为在Hamilton体系下的分离变量法提供了理论依据,具有深远意义。

4 无穷维Hamilton算子数值域及数值半径

Hilbert空间中有界线性算子的数值域是二次型和Rayleigh商从有限维到无穷维的逻辑上的推广,具有深厚的理论基础。正如线性算子的谱集一样,Hilbert空间中线性算子的数值域也是复平面的子集,它也蕴含有关线性算子的相关信息,甚至能够提供一些谱集不能提供的信息。例如,一个线性算子的数值域是实数集蕴含该线性算子是对称算子,而谱集是实数不一定是对称算子。从学术研究角度来讲,线性算子数值域的研究涉及纯理论和应用科学的诸多分支,诸如算子理论、泛函分析、C*-代数、Banach代数、数值分析、扰动理论、控制论以及量子物理等等。此外,关于线性算子数值域的研究方法也十分丰富,代数、分析、几何、组合理论、计算机编程都是非常有用的研究工具。因此,线性算子数值域以及相关问题的研究受到了诸多学者的广泛关注。鉴于此,团队围绕无穷维Hamilton算子的数值域以及有界无穷维Hamilton算子数值半径不等式问题展开研究,取得了一些成果。

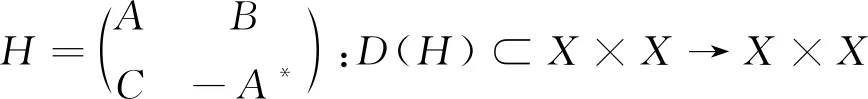
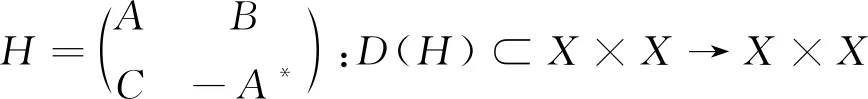
上述结论解决了无穷维Hamilton算子数值域对称问题和谱包含性质,这对于解决无穷维Hamilton算子点谱对称问题具有重要意义。