(1+1)维Mukherjee-Kundu方程的加速怪波解和呼吸子解
2021-02-01扎其劳
陈 鑫, 扎其劳
(内蒙古师范大学 数学科学学院,内蒙古 呼和浩特 010022)
0 引言
众所周知,非线性方程是数学和理论物理领域的一个重要研究内容[1],如非线性薛定谔(NLS)方程[2]、导数NLS方程[3]、Davey-Stewartson方程[4]、Kundu-Eckhaus方程等。非线性方程解是其关键内容,它可以描述许多非线性现象。近年来,非线性方程解的研究重点已经转移到寻找具有多种物理适用性的新复杂解上,如加速孤子解[5]、怪波解[6-7]、呼吸子解[8]等。
怪波和呼吸波作为两种特殊类型的非线性波,具有重要作用。1965年,Draper首次提出了怪波概念[9]。1983年,Peregrine首先得到NLS方程的一阶解析解,并用它来描述怪波现象[10]。随后,怪波相继在非线性光学[11]、海洋学[12]、Bose-Einstein凝聚[13]和金融领域[14]中被发现,怪波特别存在于一些非线性方程中。目前,怪波产生的确切机制还不完全清楚,研究怪波理论不仅对怪波理论研究具有重要意义,而且可以推动与怪波有关的其他学科的发展。
呼吸波是一种非线性波包,其能量以局域振荡的方式集中。时间呼吸子和空间呼吸子是两种主要类型的呼吸子。时间呼吸子对应于非线性方程的局部化解,其振幅随时间而变化,例如Ma呼吸子[15]。同时也存在相反的情况:呼吸波在空间上振荡并且沿着传播距离局部化,例如Akhmediev呼吸子[16]。呼吸子的研究对船舶和海洋结构物的耐波性试验和标准制定具有重要意义。
2019年,Mukherjee和Kundu提出了一个新的复非线性波方程((1+1)维Mukherjee-Kundu方程)[5]
(1)

(2)
其中,*表示复共轭,下标表示偏导数。
文献 [5]得到了方程(1)的一阶怪波解
(3)
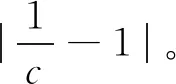
(4)
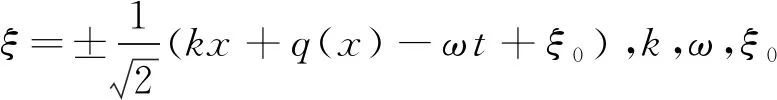
文献 [7]利用符号计算方法,导出了方程(2)的具有多个参数的高阶怪波解
(5)
其中
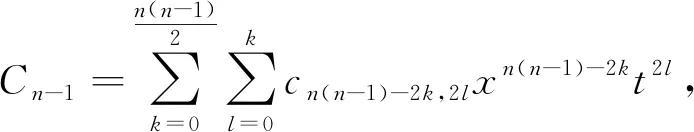
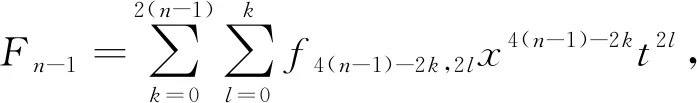
B0=C0=D-1=0。
通过对自由参数的分析,详细研究了一阶和二阶怪波解在时空中的非线性动力学特征。此外,方程(2)的一些周期波和加速周期波解还可以用Jacobi椭圆函数表示[7]
(6)
其中,k,ω,ξ0和C是常数,q(x)是一个关于x任意函数,r(0≤r≤1)是模数。
值得一提的是,加速暗孤子和加速周期波解分别在方程(4)和方程(5)中给出,那么方程(2)是否存在一个加速的怪波解?本文的目的就是利用符号计算方法构造出方程(2)的加速怪波解和呼吸子解,并且给出这些解的图像。重要的是方程(2)的加速怪波解包含一个自由函数q(x),它可以产生有趣的拓扑性质。
1 符号计算方法
根据文献 [7],利用符号计算法将高阶怪波解推广到高阶加速怪波解,具体步骤如下:
步骤1考虑方程(2)的平面波解,其形式为
ψ=eiA t,
(7)
其中A是一个实数。
步骤2假设方程(2)的一般加速怪波解为
(8)
其中
B0=C0=D-1=0,
q(x)是一个关于x的任意函数。
步骤3将(8)式代入方程(2),收集xstm和q(x)的同次幂的系数,并设其为零,得到一个多项式方程组。通过数学软件Mathematica求解这些多项式方程,可以确定ai,j,bi,j,ci,j,di,j,fi,j,gi,j(i,j∈{0,2,4,…}),以及某些参数值之间的关系。
步骤4将ai,j,bi,j,ci,j,di,j,fi,j,gi,j(i,j∈{0,2,4,…})的值代入(8)式,可得方程(2)的加速怪波解。
2 加速怪波解
根据上述符号计算法,考虑方程(2)的一阶和二阶加速怪波解。
2.1 一阶加速怪波解
当n=1,一阶加速怪波解的形式为
(9)
将(9)式代入方程(2),收集xstm(s∈{0,1,2,3,4};m∈{0,1,2,3,4})和q(x)的同次幂的系数,并设其为零,得到一个多项式方程组
(10)
求解方程组(10),得
(11)
将(11)式代入(9)式,就得到一阶加速怪波解
(12)
通过对任意函数q(x)的自由选择,(12)式可以产生方程(2)的一些作用解。
(1) 令q(x)=eα11x+β11,得到扭结波和一阶怪波相互作用解
(13)
解(13)的三维图如图1所示。
(2) 令q(x)=cosh (α12x+β12),得到孤子和一阶怪波相互作用解
(14)
解(14)的三维图如图2所示。
(3) 令q(x)=3cos (α13x+β13),得到周期波和一阶怪波相互作用解
(15)
解(15)的三维图如图3所示。
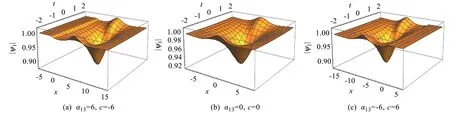
图1 扭结波和一阶怪波解的演化(13) (a0,2=2, a0,0=4, a2,0=1, β13=1/2, a2,0=1, β12=1/2)

图2 孤子和一阶怪波解的演化(14) (a0,2=2, a0,0=4, a2,0=1, β13=1/2)
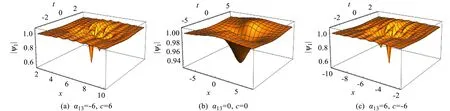
图3 周期波和一阶怪波解的演化(15) (a0,2=2, a0,0=4, a2,0=1, β13=1/2)
2.2 二阶加速怪波解
当n=2,可导出二阶加速怪波解
(16)
其中

2a(b0,0+b2,0(x-c)2)(x-c)+q(x),
a,a0,0,a2,0,a4,0,b0,0,b2,0,c是7个自由参数,q(x)是一个关于x的任意函数。
通过对任意函数q(x)的适当选择,(16)式可以产生方程(2)的弹性碰撞解。
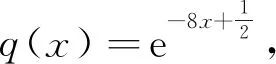

(3) 令q(x)=cos (8x),代入(16)式,得到方程(2)的周期波和二阶怪波的相互作用解。波的相互作用情况如图6所示。

图4 扭结波和二阶怪波解的演化(16)
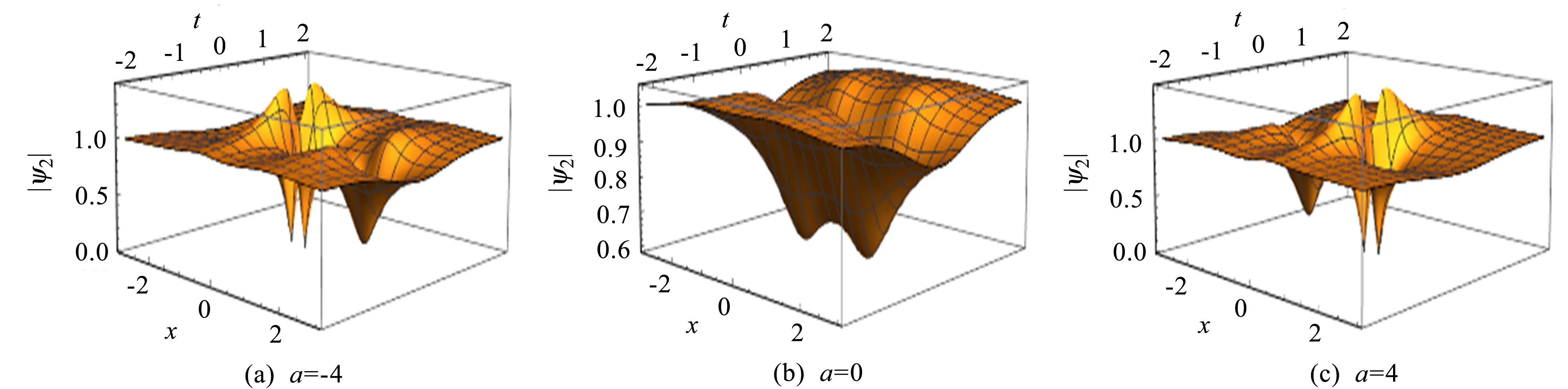
图5 孤子和二阶怪波解的演化(16)

图6 周期波和二阶怪波解的演化(16) (q(x)=cos (8x), a0,0=2, a2,0=1, a4,0=1, b0,0=-1, b2,0=1, c=0)
图4描述了扭结波和二阶怪波相互作用解的弹性碰撞。通过改变a的值,扭结波和二阶怪波的相互作用呈现迎头碰撞的形状。在图4(a)中,扭结波和两个反怪波分开,扭结波和较浅的反怪波在左侧,较深的反怪波在右侧; 在图4(b)中,扭结波和两个反怪波有正面碰撞; 在图4(c)中,碰撞后的扭结波和两个反怪波保持形状和速度不变,只是位置发生了改变: 扭结波和较深的反怪波在左侧,较浅的反怪波在右侧。类似地,孤波和二阶怪波相互作用解以及周期波和二阶怪波相互作用解的弹性碰撞分别表示在图5和图6中。
3 呼吸子解
假设方程(2)的呼吸子解为
(17)
其中ξ=ax+bt+ξ0,θ=cx+dt+θ0,实参数a,b,c,d,A,B,C,D,p,q,ξ0和θ0之后将被确定下来。
将(17)代入方程(2),利用sinh2ξ=cosh2ξ-1和sin2θ=1-cos2θ,得到了一组关于a,b,c,d,A,B,C,D,p,q的非线性代数方程组
(18)
借助Mathematica,可求得该非线性代数方程组的两类解。
情况1
(19)
情况2
(20)
将(19)式代入(17)式,得到方程(2)的Ma呼吸子解
(21)

Ma呼吸子解(21)是以时间t为周期的呼吸子,该波的形状如图7中的三维图(a)和等高线图(b)所示。
将(20)式代入(17)式,得到方程(2)的Akhmediev呼吸子解
(22)
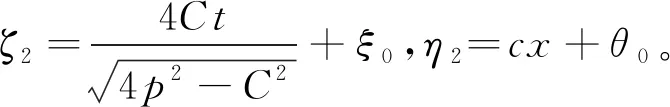
Akhmediev呼吸子解(22)是以空间x为周期的呼吸子,该波的形状如图8中的三维图(a)和等高线图(b)所示。
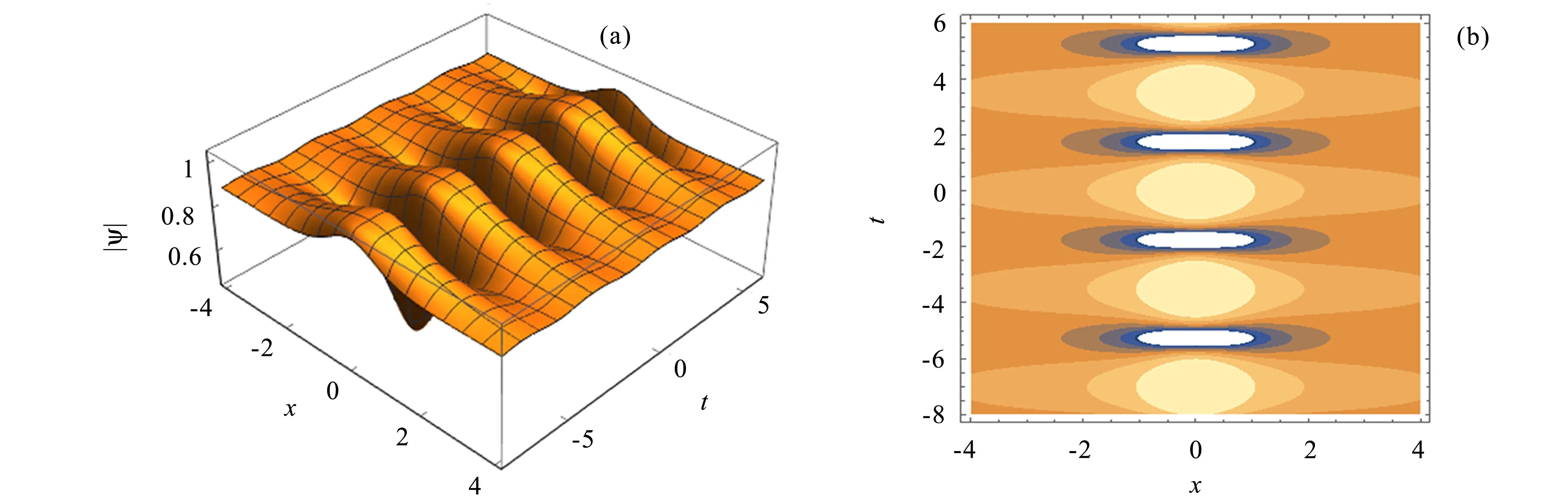
图7 Ma呼吸子解(21) (p=2, q=1, D=1, a=1, ξ 0=0, θ 0=0)

图8 Akhmediev呼吸子解(22) (p=2, q=1, C=1, c=1,ξ 0=0, θ 0=0)
4 结论
(1+1)维Mukherjee-Kundu方程(2)是孤子理论中一个有趣的新方程。通过符号计算法,给出方程(2)的包含任意函数q(x)的一阶和二阶加速怪波解,当函数q(x)选择某些特殊函数时,将得到扭结-怪波、孤子-怪波、周期波-怪波解。借助于符号计算法,本文也给出了方程(2)的Ma呼吸子解和Akhmediev呼吸子解。通过图形展示了所得解的性质,如图1至图8所示。
