区间值数据的代价敏感特征选择

刘 琼 ,代建华* ,陈姣龙

（1.智能计算与语言信息处理湖南省重点实验室，湖南师范大学，长沙，410081；2.湖南师范大学信息科学与工程学院，长沙，410081）

随着社会的快速发展，存在的数据也越来越多，数据中往往包含有不确定性，而区间数据是一个重要的类型.一方面，客观上由于测量、计算所带来的数据误差往往不是一个确定的数，而是一个区间范围；另一方面，主观上人们在描述和理解某些数据时，也更倾向一个区间范围，而不是一个确定的值，比如身高、体重、收入等.高维的区间值数据在现实生活中广泛存在，因此研究区间值数据的特征选择具有重要的意义.针对区间值数据的特征选择问题，学者已进行了相关研究.例如，Du and Hu［1］提出区间值有序决策表的近似分布约简.Yang et al［2］提出基于α 序关系区间值信息系统属性约简.Dai et al［3］在区间值决策系统中利用概率方法建立优势度的模糊粗糙集模型，并利用该模型进行近似分布约简.Li［4］提出基于区间值信息系统的模糊概念格的特征选择方法.Dai et al［5］提出基于不完备区间值决策系统的特征选择.尹继亮等［6］提出区间值决策系统的局部属性约简.Shu et al［7］提出基于不确定度量的区间值缺失属性约简.闫岳君和代建华［8］提出区间序信息系统的无监督特征选择.

值得注意的是，上述针对区间数据的特征选择方法没有考虑数据自身的测试代价和误分类代价.代价敏感在数据挖掘和机器学习中得到了广泛的关注［9-14］.在代价敏感的应用中，代价可以用许多不同的单位来度量，例如在医学领域里，代价可以是非癌症患者被误判为癌症患者的可能.在图像识别中，代价可以是被错误分类的损失.本文考虑到测试代价和误分类代价，研究代价敏感区间数据特征选择.首先，利用邻域粗糙集给出区间值邻域的概念，并通过区间值邻域进行分类，进而重定义基于区间值邻域的熵结构；其次，构造了区间值系统下的代价敏感函数，引入测试代价和误分类代价，并提出基于代价敏感的区间值特征选择方法；最后，通过实验验证了本文方法的有效性.本文的主要贡献有：

（1）利用KL 散度度量两个区间值之间的关联，并构造了区间值邻域，进而重新定义了区间值邻域的熵结构；

（2）构造区间值系统下的代价敏感函数，代价敏感函数有效地考虑了区间值数据自身的测试代价和误分类代价；

（3）提出基于代价敏感的区间值特征选择方法，该方法可以选择代价较小但拥有较多有效信息量的特征.

1 预备知识

本节重点回顾一些相关概念.

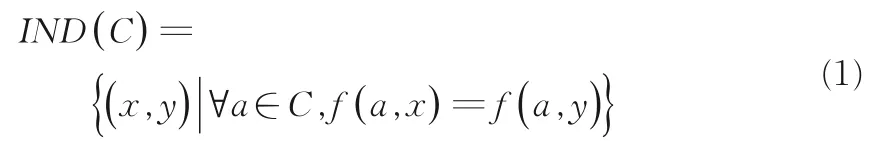
显然，IND(C)具有自反性、对称性和传递性.U/IND(C)表示所有等价类IND(C)的族，可以简写为U/C.

定义1是一个决策信息系统，其中U是非空有限对象集合，称为论域；C为条件特征集合，D为决策特征集合；V是所有特征域的并集，B⊆C，关于特征集B的信息熵定义如下：

定义2是一个决策信息系统，其中U是非空有限对象集合，C为条件特征集合，D为决策特征集合；V是所有特征域的并集，B，Y2，…，Ym} .特征集B和K的联合熵定义为：

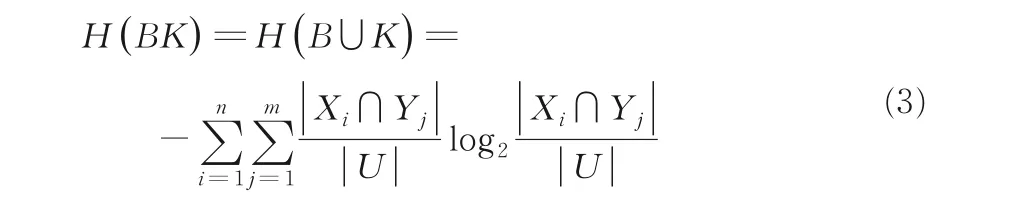
定义3是一个决策信息系统，其中U是非空有限对象集合，C为条件特征集合，D表示决策特征，V是所有特征域的并集，…，Ym} .条件特征集P关于决策特征D的条件熵定义为：

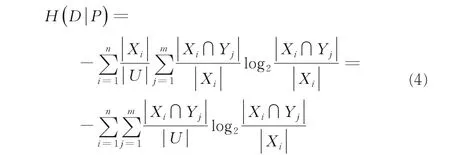
定义4是一个决策信息系统，其中U是非空有限对象集合，C为条件特征集合，D表示决策特征，V是所有特征域的并集，…，Ym} .特征集合P和决策特征D的互信息定义为：

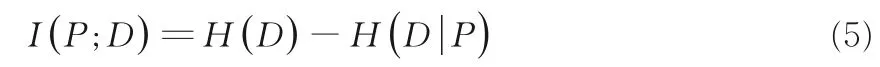
对于一个正态分布，μ是数学期望，σ是标准差，x位于区间(μ-3σ，μ+3σ)外的概率小于0.3%.在实际问题中，往往认为当置信水平达到95%时，已具备统计学意义.考虑到区间值数据为一段有限区间，而分布是无限的，因此本文通过使用合适的参数，使得区间尽可能落在95%的置信区间内.任意给定一个区间[a，b]，本文取区间中值作为期望值作为标准差，这样就构成一个正态分布S～N(μ，σ2)，以满足该区间[a，b]具备统计学意义［15］.

定义5设P～N是两个正态分布，则关于P，Q两个分布之间的距离可利用KL 散度定义：

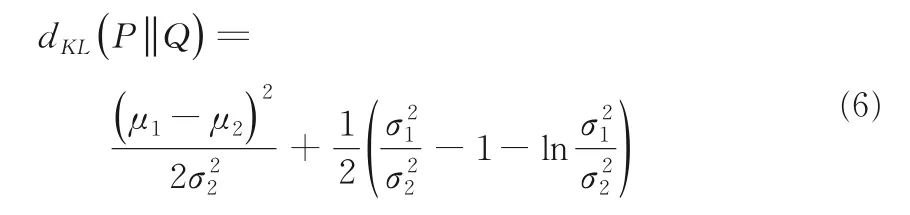
考虑到KL 散度不满足对称性，因此对于两个分布之间的距离度量可重定义为如下形式：

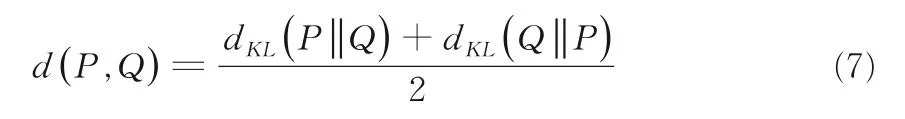
2 基于区间分类误差的邻域粗糙集

本节提出基于区间分类误差的邻域粗糙集模型（Interval-Classification-Error-Based Neighborhood Rough Set Model）并证明一些相关性质.是一个邻域决策信息系统，其中U={x1，x2，…，xn}是n维对象集合，称为论域；C为所有条件特征集合；D表示决策特征，N为样本关于特征的邻域映射函数，其中∀x∈U，a∈C，Na(x)={y∈U|da(x，y)≤δ} .

定义6是一个邻域决策信息系统，其中U={x1，x2，…，xn}为n维对象集合，C为所有条件特征集合；D表示决策特征，N为样本关于特征的邻域映射函数.设a∈C，x∈U.对于任意对象区间值[n，m]，首先取区间中值作为期望值作为标准差，这样就构成一个满足统计学意义的正态分布，然后基于式（6）和式（7）定义对象x在特征a下的邻域：

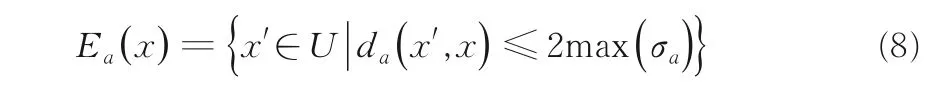
da(x'，x)表示对象x'和x在特征a下的两个分布之间的距离，max(σa)表示特征a下所有对象的最大标准差，也称为上边界域.

设特征a的测量误差值都在区间[-b，b]之间，对特征a来说，对象x的真实值是a'(x).但是由于测量误差的原因，其测量值a(x)会在一个区间范围内，即a'(x)-b≤a(x) ≤a'(x)+b.特别地，在极端情况下，同一对象的观测值可能是从端点取得的，即a-b或a+b.则有(a'(x)+b)-(a'(x)-b)=2b，所以观测值不应超过2b，故本文的邻域差设计为2max(σa).

定义7是一个邻域决策信息系统，其中U={x1，x2，…，xn}为n维对象集合，C为所有条件特征集合，D表示决策特征，N为样本关于特征的邻域映射函数.设B⊆C，∀x∈U，对象x关于特征集合B的邻域定义为：

根据定义7 得出以下性质：

性质1是一个邻域决策信息系统，P⊆C，∀x∈U，EP(x) 满足以下性质：

（1）自反性：∀x∈U,x∈EP(x)；

（2）对称性：∀xi，xj∈U，如果xj∈EP(xi)则xi∈EP(xj).

证 明

（1）根据式（8）和式（9），∀a∈P，x∈U，有da(x'，x) ≤2 max (σa)，而da(x，x)=0 且max (σa)≥0，则∀x∈U,x∈Ea(x)，然后根据式（9）可得∀x∈U,x∈EP(x).

（2）因为∀xi，xj∈U，xj∈EP(xi)，根据式（9）可知，∀a∈P，xi，xj∈U有xj∈Ea(xi)，从式（8）可以明显看出Ea(x)具有对称性，故∀a∈P，xi，xj∈U有xi∈Ea(xj)，从而有xi∈EP(xj).

给定一个非空特征集合P，RP是定义在特征P上的邻域等价关系，用关系矩阵?M(RP)表示：

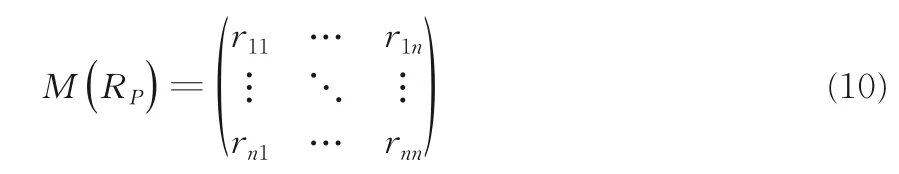
其中，rij是xi和xj的关系值，也可以写作RP(xi，xj)，n=|U|，∀xi，xj∈U，若xj∈EP(xi)或xi∈EP(xj)则rij=1，否则rij=0.

根据性质1 可以得到RP满足自反性rii=1 和对称性rij=rji.

任意给定一个非空特征集合P1，P2，RP1，RP2是分别定义在特征集合P1，P2上的邻域等价关系.∀x，y∈U，几种关系矩阵的运算方式定义如下：

定义8[xi]R基数定义如下：

定义9给定一个邻域决策信息系统NS=，其中U={x1，x2，…，xn}为n维对象集合，C为所有条件特征集合，D表示决策特征，N为样本关于特征的邻域映射函数.设A⊆C，R为特征集A上的邻域等价关系.关于特征集A的信息熵可以定义为如下形式：

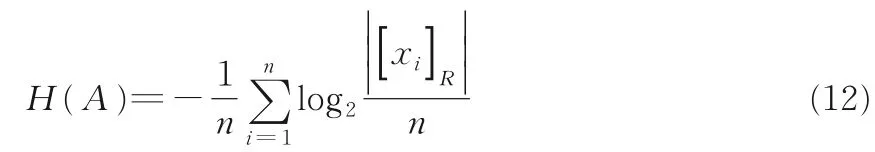
定义10给定一个邻域决策信息系统NS=其中U={x1，x2，…，xn}为n维对象集合，C为所有条件属性集合；D表示决策属性，N为样本关于属性的邻域映射函数.设B，K⊆C，[xi]B和[xi]K分别是属性集B，K上的等价类.关于属性集B和K的联合熵的定义如下所示：

RB，RK分别表示定义在属性集B，K上的邻域等价关系.

定义11给定一个邻域信息系统NS=，其中U={x1，x2，…，xn}为n维对象集合，C为所有条件属性集合；D表示决策属性，N为样本关于属性的邻域映射函数.设P⊆C，[xi]P和[xi]D分别是属性集P，D上的等价类.条件属性集P关于决策属性D的条件熵定义如下：

为了便于理解式（8）的邻域Ea(x)和最大标准差max (σa)，下面用例子来说明.

例1一个区间决策信息系统由表1 构成.U={x1，x2，…，x6}，C={a1，a2，a3} 且决策属性d在论域U上的划分为U/d={{x1，x2，x3}，{x4，x5，x6} }.设X1={x1，x2，x3}，X2={x4，x5，x6} .首先基于表1 给出属性下的最大标准差max(σa1)=9.375，ma x(σa2)=3.675，max(σa3)=0.0575.根据式（8）可以计算出所有属性的邻域，结果如表2所示.设B1={a1，a2}，B2={a1，a3}，B3={a2，a3} .根据表2 和式（9）可以计算出B1，B2，B3邻域EB1(x)，EB2(x)，EB3(x)分别为：

表1 区间决策系统一个实例Table 1 An example of interval decision system

表2 邻 域Table 2 The neighborhoods

3 基于代价敏感的特征选择问题

通常数据本身有测试代价，即获得数据精度所付出的代价，并且现实生活中的数据因为一系列原因可能导致一定的误分类代价.因此，本节提出基于区间值数据的测试代价和误分类结构.

3.1 代价函数对于一个邻域决策信息系统其中U={x1，x2，…，xn}为n维对象集合，C为所有条件属性集合；D表示决策属性，N为样本关于属性的邻域映射函数.设a∈C，tc为测试代价函数，tc(a)max是属性a下所有对象的最高测试代价，即属性a获得最高数据精度所付出的测试代价，则每个对象的最高总测试代价为tc本文给定属性a，测试代价函数根据应用背景以不同的形式表示，本文的线性函数的测试代价函数设计为：

其中，λa∈[0，1 ]是测试代价的一个调节因子，调节所有对象的测试代价，使每个对象的总测试代价趋于平衡.

对任意B⊆C，每个对象总测试代价（Total Test Cost，TTC）定义为：

设mc为误分类代价函数，(n，m)为从类n到类m的误分类.误分类代价函数定义如下：

其中，β(n，m)＞0 是一个惩罚因子，用于惩罚从类n到类m?误分类的对象x.另一种误分类代价常数函数定义如下：

MC(n，m)为从类n分类到类m的误分类代价，是一个常数.

3.2 平均总代价的计算考虑到一个对象往往属于多个邻域粒，可能导致误分类代价被重复计算.本文使用文献［16］中新的误分类代价计算方法，可以避免过多的重复计算.

（1）如果∀y∈EB(x)且d(y)=d(x)，则把对象x分类到本身所在类，所以mc(x，B)=0.

（2）如果∃y∈EB(x)且d(y)≠d(x)，考虑到同一邻域粒的对象是不可区分的，假设它们在分类时具有相同的决策值，那么可以对x进行分类，使EB(x)中所有对象的误分类总代价最小化，从而得到相应的mc(x，B).

则平均误分类代价（Average Mis-classification Cost，AMC）定义如下：

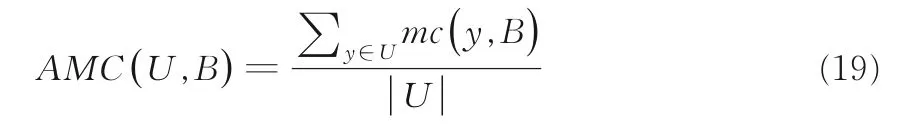
因为对象的总测试代价是相同的且等于TTC(B)，所以平均总代价（Average Total Cost，ATC）定义如下：

例2（续例1）给定：tc(a1)max=20，tc(a2)max=63，tc(a3)max=15，λa1=0.3，λa2=0.4，λa3=0.2，则tc(C)max==98.设B={a1，a3}，因为tc(a1)=20×0.3=6和tc(a3)=15×0.2=3，则有TTC(B)=6+3=9.那么设β(1，2)=40 和β(2，1)=10，有mc(B)(1，2)=40×9=360，mc(B)(2，1)=10×9=90.

根据例1 所计算的邻域，有：

EB(x1)={x1，x6}，EB(x2)={x2，x6}

EB(x3)={x3}，EB(x4)={x4，x6}

EB(x5)={x5，x6}，EB(x6)={x1，x2，x4，x5，x6}

结合表1，将每个对象按照其邻域进行分类，得到误分类代价.具体来说，对于对象x1，假设邻域EB(x1)中所有对象都被分类到类“1”，则邻域EB(x1)中所有对象的误分类总代价为90.相反，如果将邻域EB(x1)中所有对象分类到类“2”，则相应的误分类总代价为360.因此将邻域EB(x1)中所有对象分类到类“1”以获得较少的误分类总代价.根据表1，对象x1本身决策属性为类“1”，所以对象x1被正确分类，mc(x1，B)=0.对于对象x6，如果把邻域EB(x6)中所有对象分类到类“1”，则邻域EB(x6)中所有对象的误分类总代价为90×3=270.相反，如果将邻域EB(x6)中所有对象分类到类“2”，则相应的误分类总代价为360×2=720.因此，选择将邻域EB(x6)中所有对象分类到类“1”，在这种情况下，x6本身决策属性为类“2”，但被误分类到类“1”，所以mc(x6，B)=90.同理可得mc(x2，B)=mc(x3，B)=mc(x4，B)=mc(x5，B)=0.

根据式（19），AMC(U，B)=90 ∕6=15，然后根据式（20）得到ATC(U，B)=9+15=24.

代价敏感属性约简的目的是找到一个属性子集，并使得总代价最小化［17-21］，尽可能多地保留原始数据中的信息.基于代价敏感区间值属性约简的问题形式定义如下：

4 基于代价敏感区间值特征选择算法

本节提出基于代价敏感的区间值属性约简算法，算法具体步骤展示在算法1 中.

算法1 遵循Liao et al［16］讨论的添加-删除策略，主要包含三个步骤：第一步，初始化全局变量；第二步，选择出相应的属性子集B；第三步是删除阶段，根据属性B中的平均总代价来删除冗余的属性.

分析时间复杂度.对于选择属性阶段，最坏的情况下，while 循环m次，即所有条件属性都被选择；while 循环体内部最坏的情况下for 循环将执行次，for 循环体内部计算条件熵的时间复杂度为O(nm)，其中n为对象个数.故在选择属性阶段时间复杂度为O(nm3).对于删除阶段，最坏的情况下属性全部被删除，这种情况while 循环执行|B|次，相应的for 循环将执行次，for 循环体内部平均总代价的时间复杂度，根据式（20）可知为O(max(n，m))，故删除阶段时间的复杂度为故在最坏的情况下算法1的时间复杂度为O(nm3).

5 实验与结果

为了验证提出算法的有效性，在11 个真实数据集上进行了实验.数据集都是从UCI 数据库中获得，其中Face，Fish，Water 条件属性值都是原始区间值数据，其他数据集的原始属性值为实值.表3 展示了实验数据的详细信息.

5.1 实验准备在进行实验之前，首先将实值数据进行区间化预处理，根据3.1 节对实验数据进行代价函数预处理，先对实验数据的属性集设置测试代价.对于属性数目小于15 的数据集，设最高测试代价tc(a)max为分布在[20，100 ]内的均匀分布的随机整数，而其他数据集则设置在[20，200 ]内，测试代价调节因子λa∈[0，1 ]，设置误分类代价惩罚因子β(n，m)为[10，100 ]内的整数，误分类代价常数函数MC(n，m)设为[5000，50000]内的整数.例如Water 数据集中有两个类，分别为类1 和类2，设置惩罚因子β(1，2)=20 和β(2，1)=50；Face 数据集中有九个类，设置误分类代价常数函数MC(n，m)=10000.

表3 数据集介绍Table 3 The introduction of datasets

本文所有实验都在相同的软硬件环境下进行.CPU：Intel（R）Core（TM）i5-9300H CPU @2.40 GHz；RAM：16.0 GB；操作系统：Windows 10；Matlab 版本：Matlab 2019b.

5.2 实验结果实验的结果展示于表4 中.如表4 所示，TTC，AMC，ATC每列下面划分为三列，第一列为未经属性约简的结果（NFSR），第二列为Dai et al［22］的方法（ARCE）经过属性约简后的结果，第三列为本文方法经过属性约简后的结果（CSIVARA）.每一行中最小平均总代价（ATC）用黑体字突出显示.

表4 中Sonar 数据集上CSIVARA 的平均总代价高于ARCE；Libras 和Waveform 数据集上CSIVARA 的最小平均总代价接近最低平均总代价；其他八个数据中CSIVARA 的最小平均总代价都远低于未约简前的和对比方法ARCE 的最小平均总代价.总体来说，CSIVARA 表现最好.

5.3 比较与分析为了进一步分析实验结果，将CSIVARA 和ARCE 的分类精度进行对比.

为了比较区间值决策信息系统上属性约简的分类性能，利用扩展的KNN 分类器进行分类性能的实验.

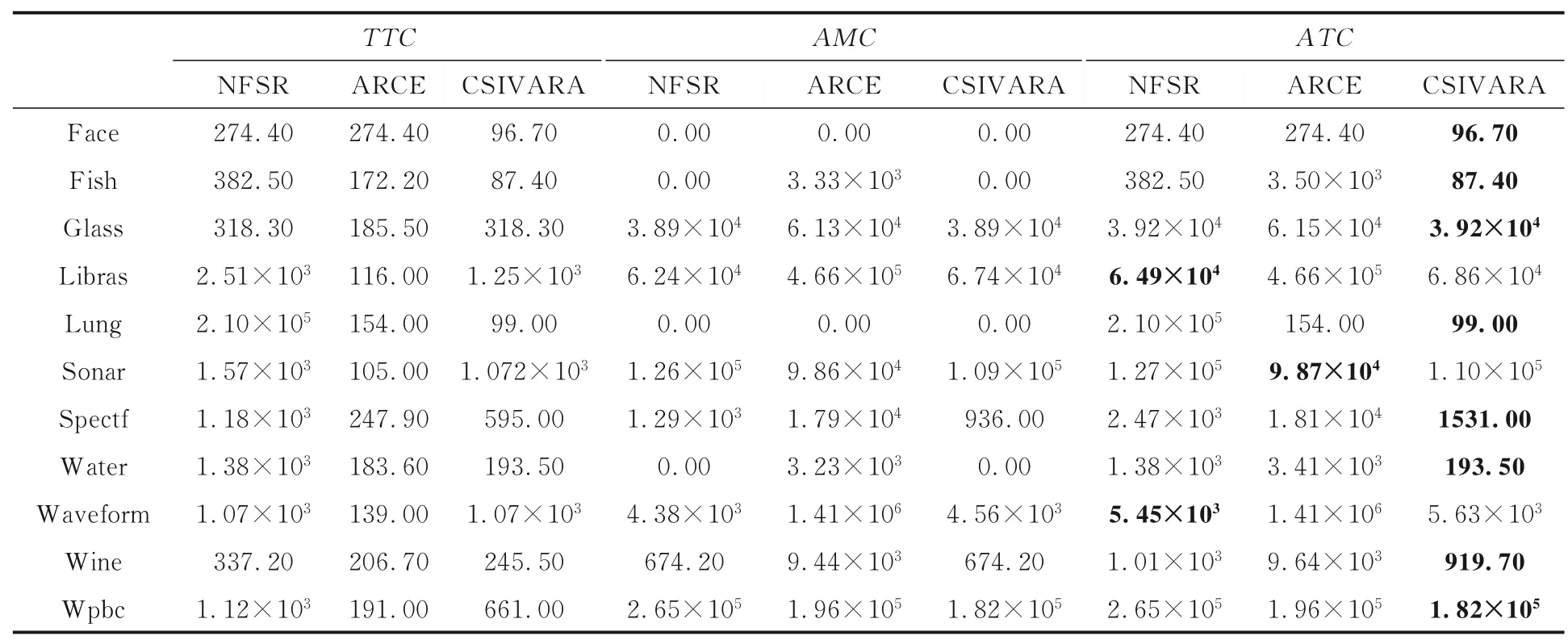
表4 三种方法的平均总代价的比较Table 4 The average total cost of the three methods

设X和Y是两个在区间值信息系统下的对象，是两个在第k个属性下的区间值.X和Y之间距离定义如下［23］：

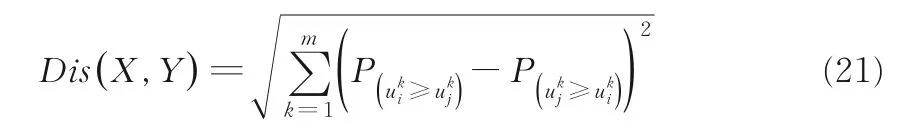
其中m为条件属性数量，是两个区间值之间的相似度.

考虑Fish 和Face 数据集的样本数太少，采用留一交叉验证的方式验证分类精度，而对于其他数据则采用十折交叉验证的方式.另外，由于随机性的问题，所有的实验结果都运行20 次，并取20 次平均值作为最终的分类精度，本文使用KNN（k=3）分类器进行实验.分类精度结果如图1 所示，可见两种方法在Face 数据集中的分类精度持平；在Lung 数据集中，CSIVARA 分类精度略低于ARCE；在Spectf 和Water 数据集中，两种方法分类精度结果非常接近；在其他七个数据集中，CSIVARA 的分类精度都优于ARCE，特别是在Libras 数据集中，CSIVARA 分类精度显著高于ARCE.

图1 在KNN (k=3)分类器上的平均分类精度结果Fig.1 Results of average classification accuracy on KNN (k=3)classifier

实验分析结果表明，CSIVARA 分类精度高于ARCE，同时还保证了平均总代价最小化.

6 结论

本文提出基于代价敏感的区间值属性约简方法，该方法根据原始数据的分布构建了基于区间值数据的代价敏感函数，充分考虑了测试代价和误分类代价对于数据的影响.最终实验表明，本文提出的方法可以在平均总代价较小的情况下有效地选择重要的候选属性.未来的工作将继续探讨区间邻域决策系统存在缺失值的情况.