基于熵的多尺度决策系统的最优尺度选择

郑嘉文 ,吴伟志,2* ,包 菡 ,谭安辉,2

（1.浙江海洋大学数理与信息学院，舟山，316022；2.浙江省海洋大数据挖掘与应用重点实验室，浙江海洋大学，舟山，316022）

粒计算模拟人类思考问题的自然模式，是知识表示和问题求解的重要工具之一，已成为大数据与智能信息处理领域的一个重要研究方向［1-5］.

在众多的粒计算模型中，粗糙集数据分析在推动与发展粒计算研究中发挥了重要作用.粗糙集数据分析中处理的数据集称为信息系统［6］，又称为信息表或对象-属性值表.原始的Pawlak 粗糙集理论利用信息系统给出数据集的训练样本上的等价类描述“粒度”，用等价关系诱导的划分来粒化数据的样本空间，用“粒”代替样本对数据进行处理，并通过计算所定义的约简（使得矛盾样本集不改变的极小特征（属性）集合）对数据集进行特征提取，最终获取聚类或分类规则或排序决策.

传统的粗糙集数据分析呈现的信息系统中每个对象与对应的属性只取惟一的一个值，这样的信息系统反映的是固定尺度下的对象信息，称为单尺度信息系统.在实际生活中人们可能要在不同粒度或尺度下对同一对象在同一属性或变量下对系统中的数据进行分析.为此，Wu and Leung［7］提出多尺度数据的粒计算分析模型，数据表的表示形式称为多尺度信息系统，又称多尺度信息表，这个数据处理模型称为Wu-Leung 模型［8］.这种数据处理的主要思想是：根据决策目标对所有属性选择同一层面的尺度或者粒度构成一个新的单尺度信息系统，然后在保持相同目标约束的前提下进行属性约简（特征选择）、决策规则提取及相应的不确定性分析.在这个模型中在保持某种性质（可以是定性的，也可以是定量的）一致的意义下选择最粗的尺度标记（称为最优尺度选择或最优粒度选择）成为在多尺度决策数据中提取决策规则前的一个关键问题，因此，近年来多尺度决策信息系统的最优尺度选择研究成为多尺度数据分析的热点问题并取得了很多成果［8-24］.

众所周知，由Shannon［25］定义的熵给出了系统结构的不确定性度量，可以用于描述各种不确定性环境下的信息内容.这种信息熵也已经成为刻画粗糙集数据分析中信息系统的知识不确定性的一种重要工具［25-31］.迄今为止，将信息熵引入多尺度信息系统的知识表示与知识获取问题中的不确定性研究几乎还是空白，本文首次将Shannon 定义的熵用于多尺度信息系统中的最优尺度选择问题，主要讨论基于熵的最优尺度选择与传统的最优尺度选择之间的关系.

1 相关的基础知识

设U是非空集合，U的子集全体记为P(U)，对于X∈P(U)用～X表示X在U中的补集，即：

1.1 信息表与近似集信息系统（有时称为信息表、数据表、对象属性值系统、知识表示系统等）的概念为对象属性值的表示提供了方便的工具.

定义1一个信息系统为一个二元组(U，A)，其中U={x1，x2，…，xn}为一个非空有限对象集，称为论域，A={a1，a2，…，am}为一个非空有限属性集，使得∀a∈A，满足a：U→Va，即a(x) ∈Va，x∈U，其中Va={a(x)|x∈U}称为a的值域.

对于任意非空子集B⊆A，记RB={(x，y)∈U×U|a(x)=a(y)，∀a∈B}.RB称为由属性B导出的不可分辨关系，它将U粒化为不可区分集合其中[x]B是对象x∈U关于属性B的等价类，即[x]B={y∈U|(x，y) ∈RB}.

从粒计算的角度来看，等价类[x]B是由属性集B确定的不可分辨元素组成的粒，属性集B将U粒化为不相交的粒族U/RB，它们是近似U的任意子集的基本元素（信息粒）.

决策系统，也称为决策信息系统，是一个二元组S=(U，C∪{d})，其中(U，C)是一个信息系统，C称为条件属性集，d∉C是一个特殊的属性，称为决策属性，可以看作映射d：U→Vd.不失一般性，假设Vd={1，2，…，r}，由决策属性d确定U上的等价关系：

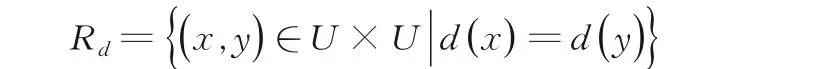
它可以把U划分成不相交的决策类：

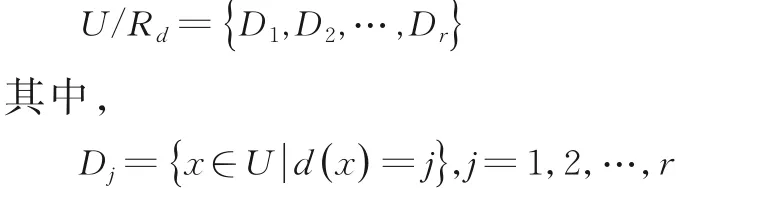
如果RC⊆Rd，那么称决策系统S=(U，C∪{d})是协调的，否则称S是不协调的.

1.2 划分与信息熵

定义2设U为一个非空有限集合，X={X1，X2，…，Xt}是U上的一个划分.X 的信息熵记为H(X)，定义如下：

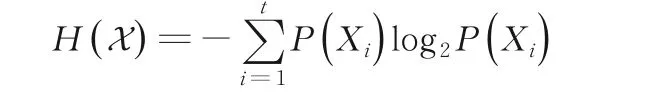
注1对于信息系统(U，A)，若B⊆A且X 是由等价关系RB产生的划分，则用H(B)来代替H(X).

命题1［27］设(U，A)为一个信息系统，且B，C⊆A.若RB=RC，则H(B)=H(C).

命题2［27］设(U，A) 为一个信息系统且B，C⊆A.若RB⊆RC且H(B)=H(C)，则RB=RC.

定义3设U为一个非空有限集合，X 和Y 是U上的两个划分.若∀X∈X，∃Y∈Y，使得X⊆Y，则称X 细于Y，或称Y 粗于X，记为另外，若进一步∃X∈X，∃Y∈Y，使得X⊂Y，则称X 严格细于Y，记为X ≺Y.

命题3［28］设U为一个非空有限集合，X={X1，X2，…，Xt}，Y={Y1，Y2，…，Yl}是U上的两个划分，若则H(X) ≥H(Y).

定义4设U为一个非空有限集合，X={X1，X2，…，Xt}，Y={Y1，Y2，…，Yl}是U上的两个划分.划分Y 相对于划分X 的条件熵记为H(Y |X)，定义如下：

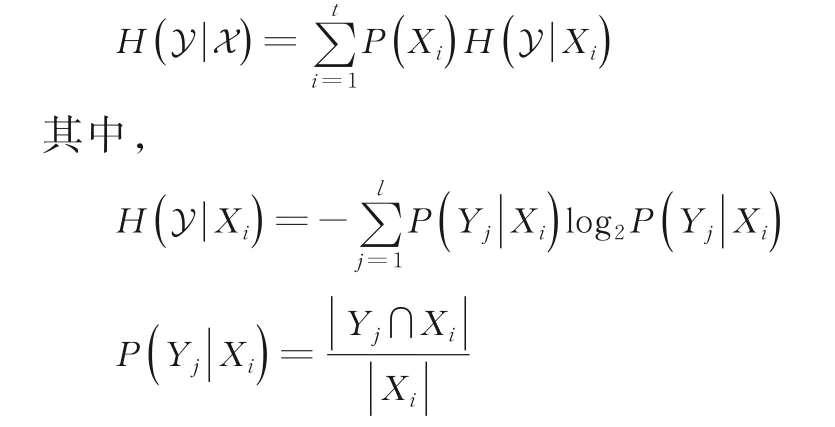
注2对于信息系统(U，A)，若B，C⊆A且Y和X 是分别由等价关系RB和RC产生的划分，则用H(B|C)来代替H(Y |X).

命题4设U为一个非空有限集合，X，Y，Z是U上的三个划分，则：

2 多尺度信息系统和多尺度决策系统

本节回顾多尺度信息系统和多尺度决策系统的概念.

在Pawlak 信息系统中，对象的特征是每个属性都有一个惟一的值.而在许多实际应用中，一个对象在同一属性下根据不同的尺度标记层面可能具有不同的值.

定义5［7］称二元组S=(U，A)为一个多尺度信息系统，其中U={x1，x2，…，xn}为一个非空有限对象集，称为论域，A={a1，a2，…，am}为一个非空有限属性集，每个aj∈A都是多尺度属性，即对于U中的每个对象xi，属性值aj(xi)可以在不同尺度上呈现不同的值.

若多尺度决策系统S在第一个（最细）尺度下的决策系统

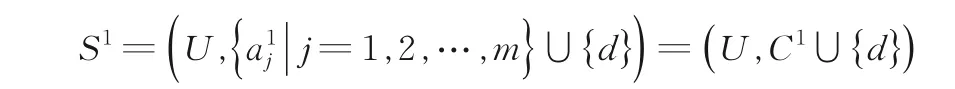
是协调的，则称S是协调的，否则称S是不协调的.

3 基于信息熵的多尺度信息系统的最优尺度选择

本节给出多尺度信息系统和协调多尺度决策系统中最优尺度与熵最优尺度的概念，并论证两者是等价关系.而在不协调多尺度决策系统中，运用广义决策和熵广义决策建立信息熵与最优尺度之间的关系，并证明广义决策最优尺度和熵广义决策最优尺度之间是等价关系.

3.1 多尺度信息系统中的最优尺度选择

定义7设：为一个具有I个尺度的多尺度信息系统，k∈{1，2，…，I}，则：

（1）若RAk=RA1，则称Sk=(U，Ak)关于S是协调的.若Sk关于S是协调的，且Sk+1（若k+1≤I）关于S是不协调的，则k称为S的最优尺度.

（2）若H(Ak)=H(A1)，则称Sk=(U，Ak)关于S是熵协调的.若Sk关于S是熵协调的，且Sk+1（若k+1≤I）关于S不是熵协调的，则k称为S的熵最优尺度.

定理1设：为一个具有I个尺度的多尺度信息系统，k∈{1，2，…，I}，则：

（1）Sk关于S是协调的当且仅当Sk关于S是熵协调的；

（2）k是S的最优尺度当且仅当k是S的熵最优尺度.

例1表1 为一个具有三个尺度和两个属性的多尺度信息系统.

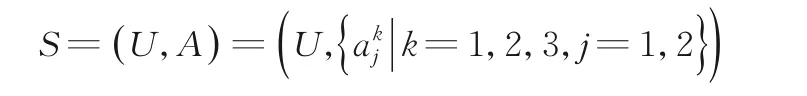
其中U={x1，x2，…，x6}，A={a1，a2}，E 表示非常好，G 表示好，F 表示一般，B 表示差，S 表示小，M 表示中，L 表示大.

表1 一个多尺度信息系统Table 1 A multi-scale information system

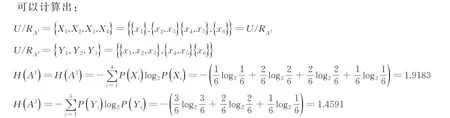
因为H(A2)=H(A1)，所以S2关于S是协调的，而H(A3) ＜H(A2)，所以k=2 是S的熵最优尺度.又因为RA1=RA2≠RA3，显然k=2 又是S的最优尺度.

3.2 协调多尺度决策系统中的最优尺度选择

对于一个协调多尺度决策系统：

为一个具有I个尺度的协调多尺度决策系统，k∈{1，2，…，I}.若Sk是协调的且Sk+1（若k+1≤I）是不协调的，则称k为S的最优尺度.

根据定义8 可以看到，协调多尺度决策系统的最优尺度是多尺度系统中进行决策或分类的最优尺度.k为最优尺度当且仅当k是使得Sk是协调决策系统的最大值.

定义9设：

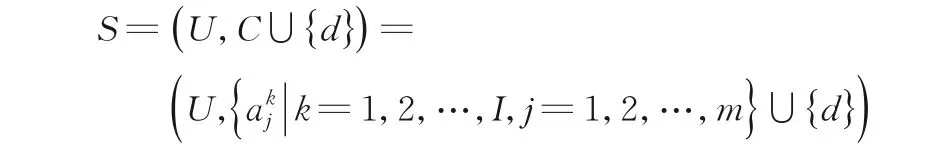
为一个具有I个尺度的协调多尺度决策系统，k∈{1，2，…，I}.若H(d|Ck)=H(d|C1)，则称Sk=(U，Ck∪{d})关于S是熵协调的.若Sk关于S是熵协调的，且Sk+（1若k+1≤I）关于S不是熵协调的，则称k是S的熵最优尺度.

定理3设：

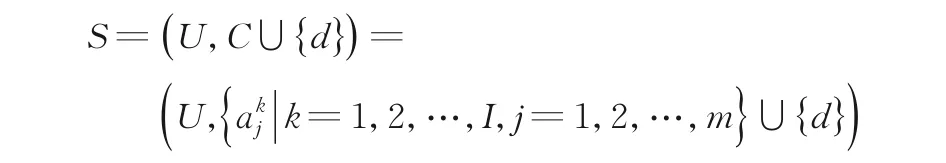
为一个具有I个尺度的协调多尺度决策系统，k∈{1，2，…，I}，则：

（1）Sk是协调的当且仅当Sk关于S是熵协调的；

（2）k是S的最优尺度当且仅当k是S的熵最优尺度.

证 明

（1）设Ck，C1和d在U上的划分分别为：

U/RCk={X1,X2,…,Xt}

U/RC1={Y1,Y2,…,Yl}

U/Rd={Z1,Z2,…,Zr}

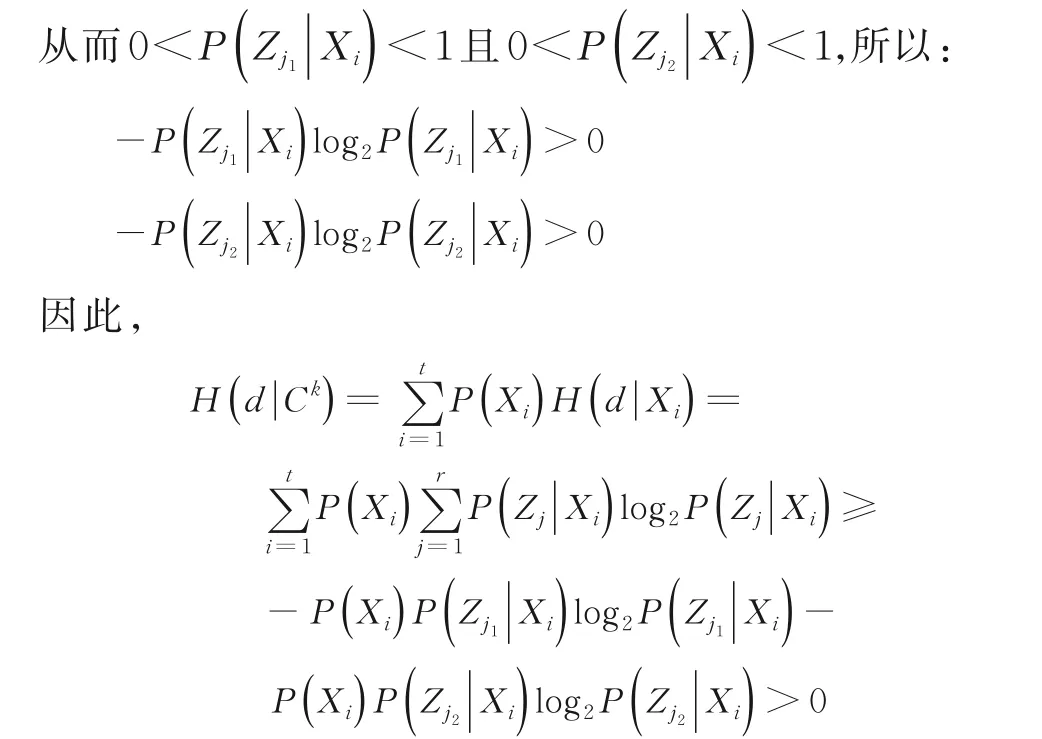
这与H(d|Ck)=H(d|C1)矛盾，所以Sk是协调的.

（2）由（1）即得.

定理4设：

为一个具有I个尺度的协调多尺度决策系统，k∈{1，2，…，I}.则k是S的最优尺度当且仅当以下条件成立：

（1）H(d|Ck)=0.

（2）H(d|Ck+1) ＞0（若k+1≤I）.

证 明由定理3 即得.

例2表2 为一个具有三个尺度和两个属性的多尺度决策系统：

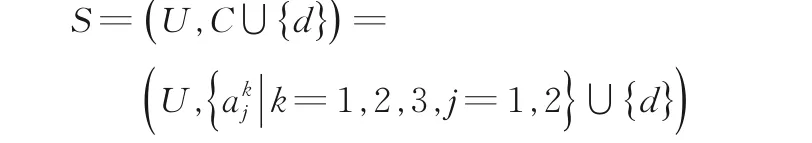
其中，U={x1，x2，…，x8}，C={a1，a2}，G 表示好，F 表示一般，B 表示差，S 表示小，L 表示大.

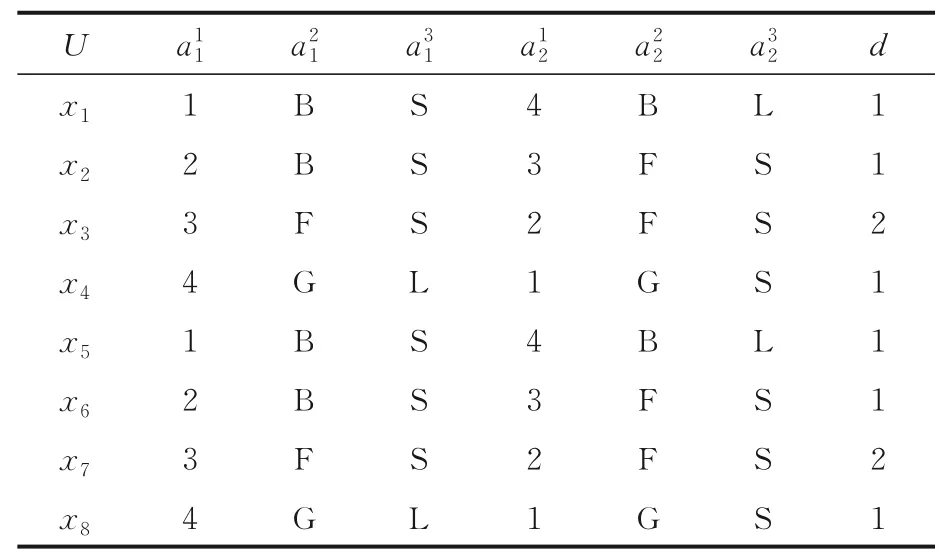
表2 一个多尺度决策系统Table 2 A multi-scale decision system

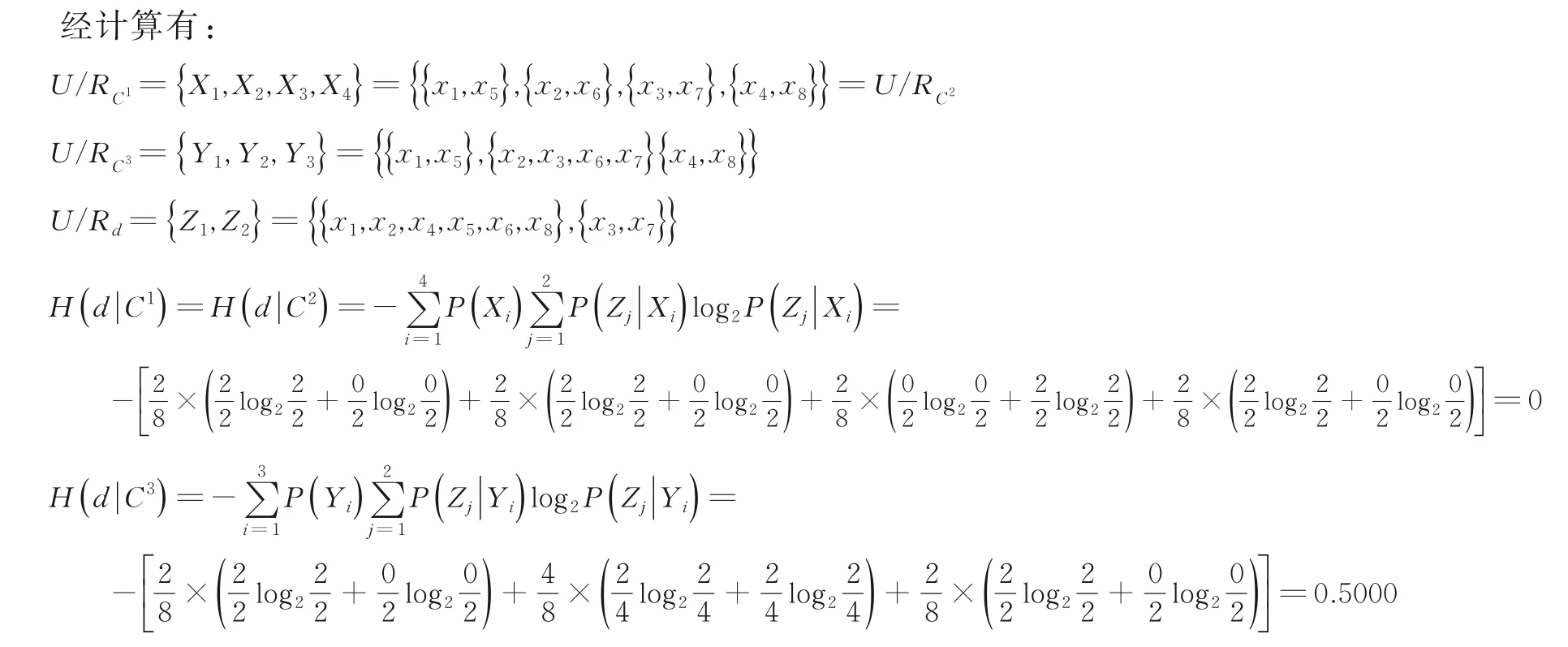
因为H(d|C2)=H(d|C1)=0，所以S2关于S是熵协调的，而H(d|C3) ＞0，因此k=2 是S的熵最优尺度.又因为RC2⊆Rd，RC3⊈Rd，因此k=2 也是S的最优尺度.

3.3 不协调多尺度决策系统的最优尺度选择

则：

（2）若H(d|Ck)=H(d|C1)，则称Sk关于S是熵协调的.若Sk关于S是熵协调的，而Sk+1（如果k+1≤I）关于S不是熵协调的，则k称为S的熵最优尺度.

在具有I个尺度的不协调多尺度决策系统中，对于k∈{1，2，…，I}，

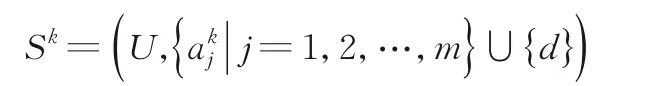
是不协调决策系统.显然，Sk关于S是广义决策协调的当且仅当Sk保持与第一个尺度（最细尺度）下决策系统S1具有相同的广义决策值.k是S的广义决策最优尺度当且仅当k是使得Sk保持与S1有相同的广义决策值的最大数.

例3表3 为一个具有两个尺度和两个属性的多尺度决策系统：

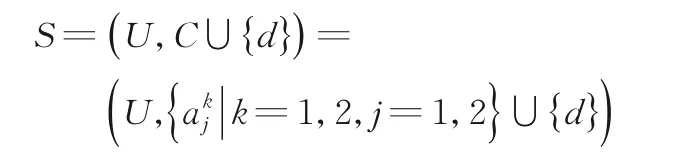
其中U={x1，x2，…，x8}，C={a1，a2}，B 表示差，F 表示一般，G 表示好，Y 表示是，N 表示否.

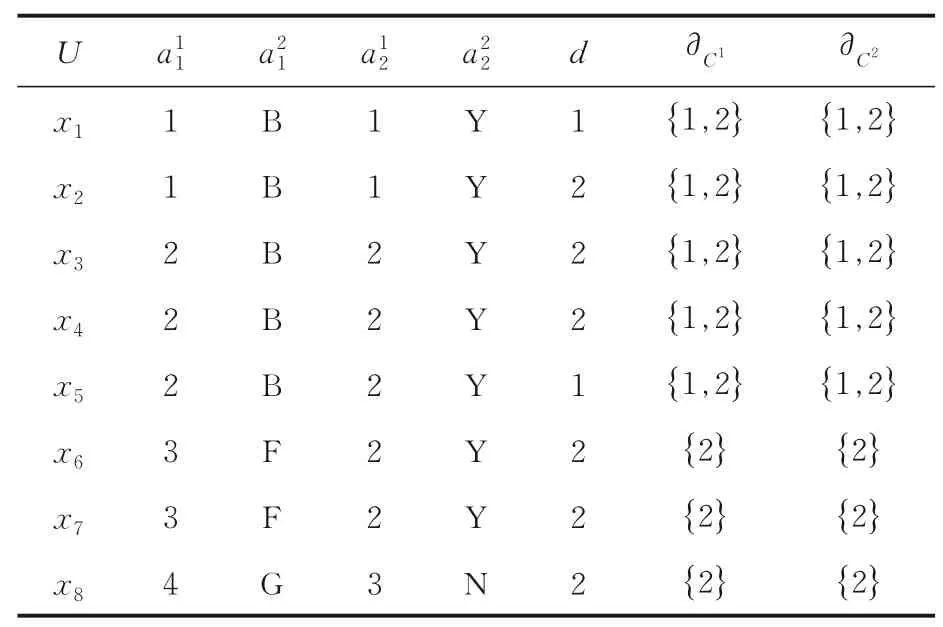
表3 一个多尺度决策系统Table 3 A multi-scale decision table

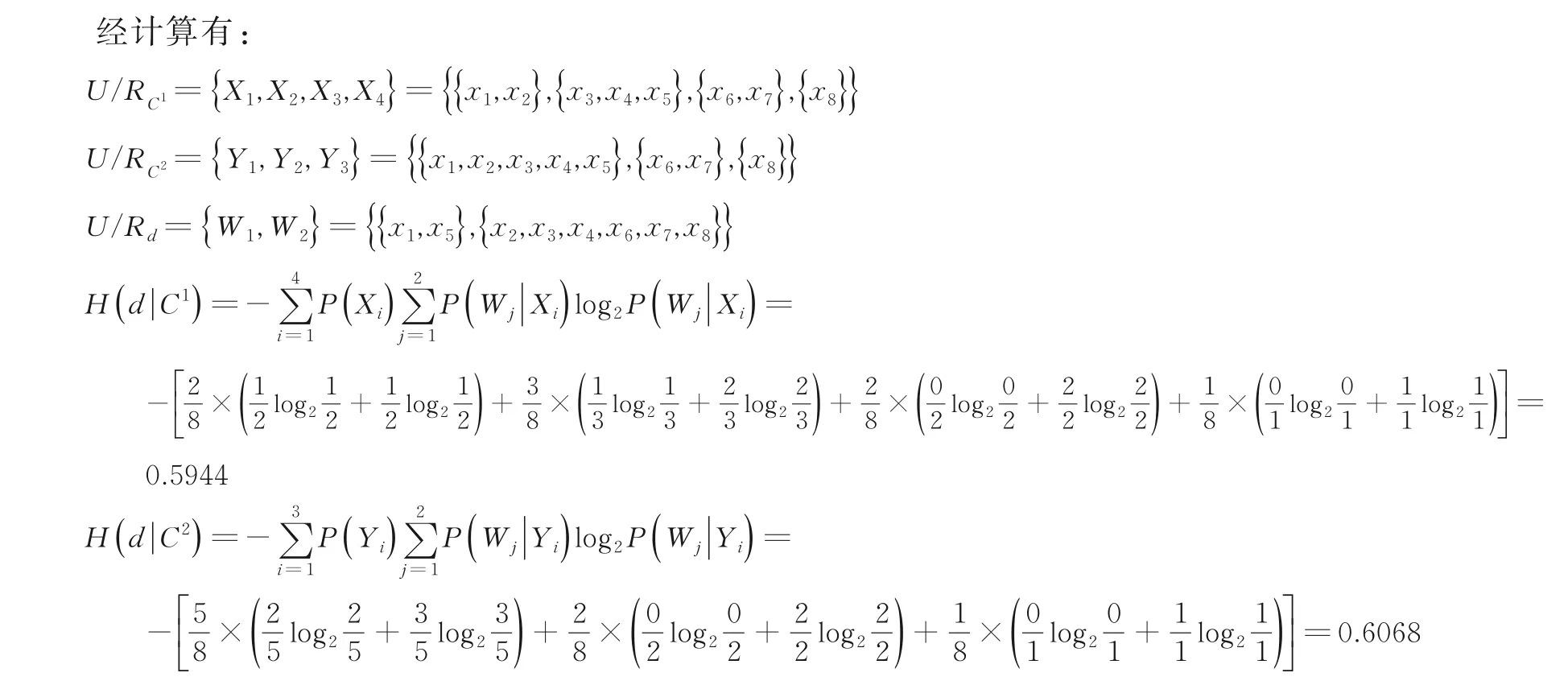
因为H(d|C2) ≠H(d|C1)，所以k=1 是S的熵最优尺度.由表可知1，…，8，所以k=2 是S的广义决策最优尺度.由此，在不协调多尺度决策系统中，广义决策最优尺度与熵最优尺度是不等价的.

定理5设：

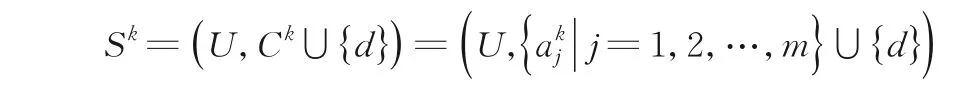
为具有I个尺度的不协调多尺度决策系统，k∈{1，2，…，I}，则：

(1)Sk关于S是广义决策协调的当且仅当Sk关于S是广义决策熵协调的；

（2）k是S的广义决策最优尺度当且仅当k是S的广义决策熵最优尺度.

证 明（1）记：

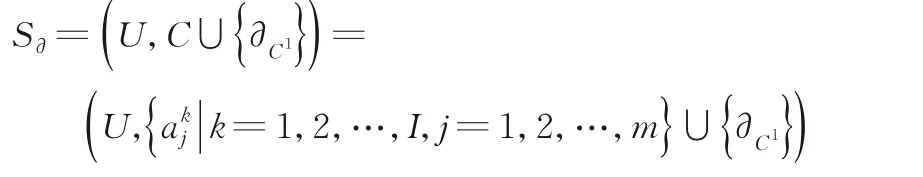
则S∂是一个协调的多尺度决策系统.又记=是协调的决策系统，因此Sk关于不协调多尺度决策系统S是广义决策协调的当且仅当关于协调多尺度决策系统S∂是协调的，由定理3 知，结论（1）成立.

（2）由（1）可得.

定理6设：

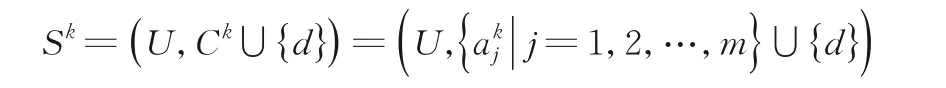
为一个具有I个尺度的不协调多尺度决策系统，对于k∈{1，2，…，I}，则k是S的广义决策最优尺度当且仅当以下条件成立：

4 总结

多尺度信息系统与多尺度决策系统的最优尺度选择问题是多尺度数据分析的一个关键问题.本文用信息熵讨论多尺度信息系统的最优尺度选择问题，定义多尺度信息系统、协调多尺度决策系统、不协调多尺度决策系统基于信息熵的最优尺度概念，证明在多尺度信息系统和协调多尺度决策系统中熵最优尺度与传统最优尺度是等价的，但在不协调多尺度决策系统中两者是不等价的.在不协调多尺度决策系统中，广义决策最优尺度与广义决策熵最优尺度是等价的.这为进一步基于信息熵的多尺度数据的知识获取奠定了理论基础，下一步将进一步研究各种复杂多尺度信息系统基于信息熵的最优尺度选择与知识获取问题.