车身用5182 铝合金板成形极限研究①

杨 刚， 王孟君， 罗嗣林

(1.台州科技职业学院,浙江 台州318020； 2.中南大学 材料科学与工程学院,湖南 长沙410083)

随着汽车产业的发展,国家对节能减排的要求不断提高,轻量化已成为汽车产业发展的主方向［1］。 铝合金密度小、比强度大、抗冲击性好,是汽车轻量化的优选材料,广泛用于车身构件中［2-4］。 在复杂冲压件生产中,成形极限曲线可作为冲压模具设计的依据,但通过实验获取成形极限曲线受设备、人员等因素影响较大且费时、费力,学者们试图建立计算模型来快速、准确地预测板料成形极限曲线［5-6］。 本文以5182 铝合金板为研究对象,构建成形极限预测模型,研究了板材初始厚度不均匀度、指数参数对成形极限曲线的影响,并与Marciniak胀形实验结果进行对比,获取了较理想的预测模型。

1 实 验

1.1 实验材料

实验用铝合金板采用1.0 mm 厚的5182-O 态铝合金冷轧板,其化学成分见表1。 该铝板生产工艺流程为:熔铸→锯切→铣面→均匀化→热轧、冷轧→退火(380 ℃,24 h)。

1.2 拉伸实验

根据GB 228—87《金属拉伸试验方法》［7］沿板材轧制方向切取0°、45°、90°的拉伸试样,实验设备为SHK-A104 万能试验机,设置应变速率为0.1 s-1。

1.3 Marciniak 胀形实验

参照Marciniak 胀形实验［8］试样尺寸切取试样,如图1 所示,其有效宽度分别为20、40、80、100、120、140、180 mm,对试样表面喷强黏着力的黑白漆。 实验设备为EC600 板材成形机,采用凡士林润滑,设置凸模下行速度为1 mm/s,压边力为30 kN。 结合GOM 应变测量系统采集胀形实验在不同成形阶段的散斑图像,基于图形算法匹配被测试样表面点的三维变形,重构匹配点的空间坐标。

图1 Marciniak 胀形实验试样示意图（单位：mm）

1.4 成形极限预测模型构建

M-K 理论基于材料损伤的角度,假设板材均匀区A 区中存在一线性凹槽B 区,B 区厚度比A 区厚度薄,板料发生变形时,其受力为平面应力状态,由于B 区厚度薄,B 区内材料最先达到材料最大承载能力。 图2 是其模型示意图。

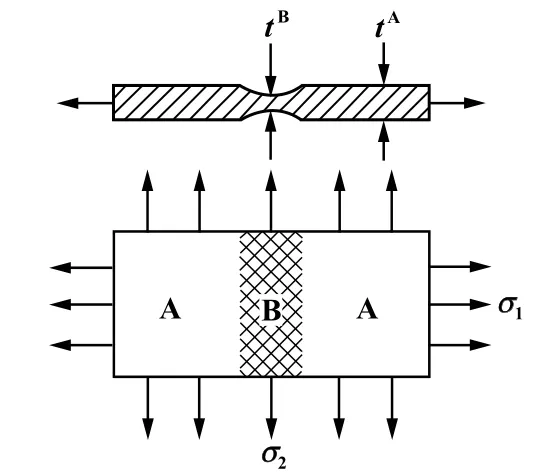
图2 M-K 理论模型示意图

M-K 理论模型主要基于如下假设:

1) 凹槽B 区内外力平衡:

式中σ1A和σ1B分别为A 区和B 区的第一主应力。

2) 变形区几何协调关系:凹槽B 区内、外基于第二主应力方向的应变增量相同,即:

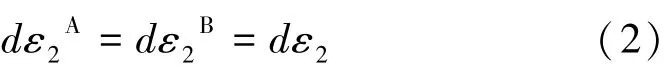
式中dε2A和dε2B分别为A、B 区基于第二主应力方向的应变增量。

3) 体积不变原则:金属板料塑性变形前后,体积保持不变。

假设第一主应力方向与凹槽相垂直,引入板料初始厚度不均匀度f0:

式中t0A和t0B分别为板料A、B 的初始厚度。

结合Hill79 屈服准则［9］和Logan-Hosford 屈服准则［10］,通过一定的迭代方法［11］,运用Matlab 对迭代过程进行编程计算,便可得出在一定板料初始厚度不均匀度f0下的极限应变值。

2 实验结果及讨论

2.1 厚向异性系数的确定

图3 为应变速率0.1 s-1时,不同轧制方向下板料的真应力-应变曲线。 测量试样应变量为15%时的宽向应变与厚向应变,得到轧制方向分别为0°、45°、90°时,对应的厚向异性系数分别为0.77、0.73、0.81,取厚向异性系数算术平均值=0.76。

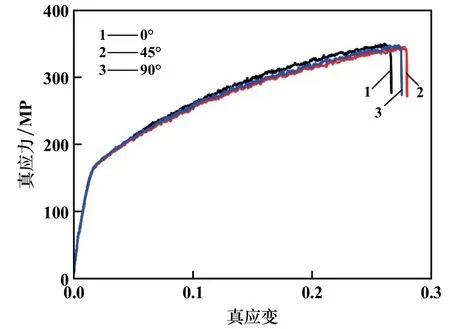
图3 板材真应力-应变曲线

2.2 应变硬化指数的确定

根据Field-Backofen 本构模型［12］,对铝合金板料σ-ε 方程式求导,得到如图4 所示的板料lnσ-lnε 关系曲线。 由图4 所得一元函数的斜率即是板料应变硬化指数n 值,经拟合,轧制方向分别为0°、45°、90°时,对应的应变硬化指数n 值分别为0.30、0.29、0.30,取平均值得=0.30。

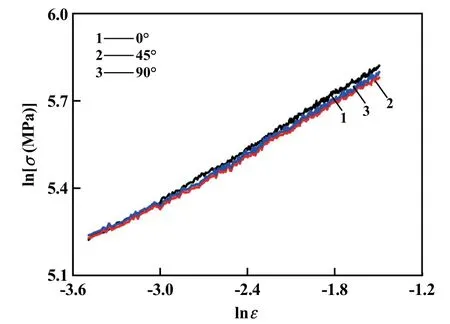
图4 板材lnσ-lnε 关系曲线

2.3 板料初始厚度不均匀度对成形极限的影响

根据Bressan 和Williams 提出的材料敏感性指数M 和厚向异性系数r 之间的线性关系式［13］为:

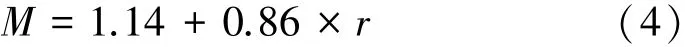
图5 板料初始厚度不均匀度对成形极限的影响

2.4 指数参数对成形极限的影响

Logan-Hosford 屈服准则中的指数参数α,取1 ～10中的偶数较为合适［14］,将厚向异性系数r、应变硬化指数n 以及f0=0.97 代入Matlab 程序,令指数参数α 分别为4、6、8,得到如图6 所示的基于Logan-Hosford 屈服准则的成形极限曲线。 由图6 可以看出,随着指数参数α 增大,成形极限应变有所下降,但第二主应变ε2=0 所对应的第一主应变ε1基本保持不变,双拉区和拉-压区曲线越平缓,且双拉区比拉-压区曲线斜率的绝对值下降更快,表明指数参数α 的变化对双拉区成形极限应变的影响大于对拉-压区成形极限应变的影响。

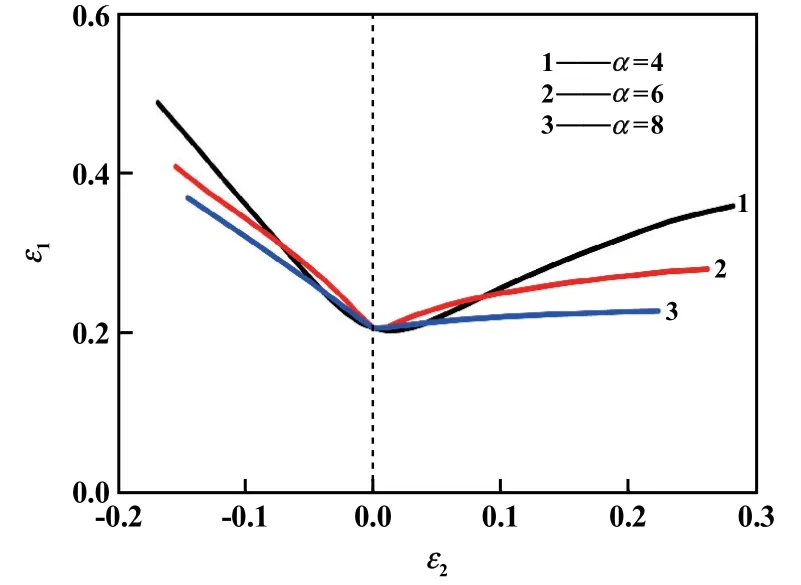
图6 指数参数对成形极限曲线的影响

2.5 基于不同屈服准则的成形极限预测结果与实验结果对比

图7为不同应变路径下Marciniak 胀形实验结果图。 基于应变测量系统采集胀形实验在不同成形阶段的散斑图像,沿试样裂纹的垂直方向做3 条平行截线,获得如图8 所示的沿试样裂纹垂直方向的应变变化曲线。 由图8 可知,在同一个试样中,3 条平行截线的应变变化曲线基本重合,在板材破裂处,第一主应变ε1最大,将不同应变路径下板料破裂处的第一主应变ε1和第二主应变ε2在图中标出,即可得出成形极限图。

图7 Marciniak 胀形实验结果

图9 为基于Hill79 和Logan-Hosford 屈服准则的成形极限预测结果与实验结果的对比图。 由图9 可知,基于Hill79 屈服准则,板料初始厚度不均匀度f0=0.97 时,实验结果与模型预测结果最吻合,其符合度为94.09%；Logan-Hosford 屈服准则作为Hill79 屈服准则的一个特例,当f0=0.97、α=6 时,实验结果与模型预测结果符合度为92.34%。

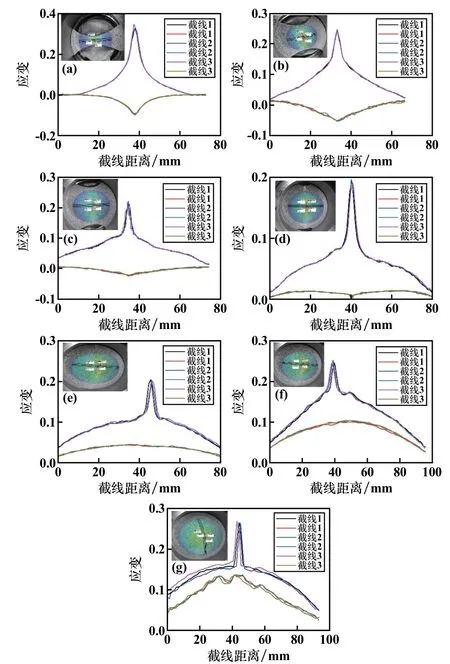
图8 沿试样裂纹垂直方向的应变变化曲线

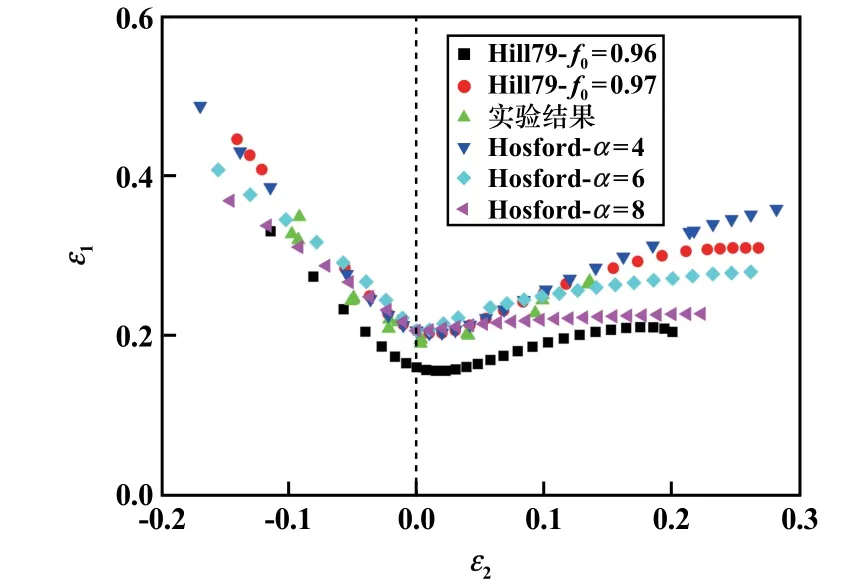
图9 预测结果与实验结果的对比

3 结 论

基于M-K 理论,并结合Hill79 和Logan-Hosford 屈服准则,构建了5182 铝合金板成形极限预测模型,将板材参数导入模型,通过Matlab 编程迭代求解,预测板料成形极限,并结合Marciniak 胀形实验进行验证。结果表明,基于Hill79 屈服准则,当板料初始厚度不均匀度为0.97 时,实验结果与模型预测结果符合度为94.09%,吻合较好,该理论模型可作为5182 铝合金板料成形极限图获取的一种方法。