问题同根 解法同源———同角三角关系的应用

◇ 山东 谢于民

同角三角关系是指同一个角的正弦值、余弦值、正切值之间的关系,例如,sin2α＋cos2α＝1,tanα＝．同角关系建立了3个三角函数之间的桥梁,在三角恒等变换、化简求解以及三角恒等式的证明中有着广泛的应用．本文通过同角关系的正向应用、逆向应用以及变形应用3个视角破解三角函数化简、求值问题．

1 正向应用

例1已知sinα·tanα＝1,则cosα＝________．

解析

由sin2α＋cos2α＝1,得sin2α＝1－cos2α,所以cos2α＋cosα－1＝0,解得．因为－1≤cosα≤1,所以(也可利用·sinαtanα＝1＞0,则α在第一象限,故cosα＞0进行取舍)．

变式已知,则tanα·sinα＝( )．

解析

点评

解题中利用同角关系进行转化时,可以从条件向结论转化,也可从结论向条件转化．例1由条件向结论转化,变式是由结论向条件转化,两种转化方式均利用了同角关系,将函数名统一,从而建立了已知与未知之间的联系．

2 逆向应用

例2已知tanα＝2,则sinαcosα＝( )．

解析

由1＝sin2α＋cos2α,得

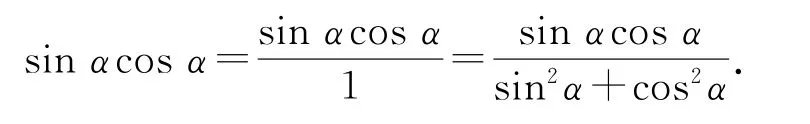
将等式右边分子、分母同时除以cos2α,可得

将tanα＝2代入,可得．故选D．

变式若,则tanα＝( )．

解析

将等式左边分子、分母同时除以cos2α得

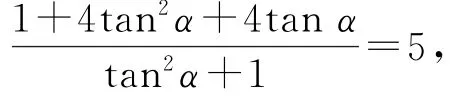
即tan2α－4 tanα＋4＝0,解得tanα＝2．故选B．

解析

用“1”代换是处理三角恒等变换问题的常用方式,上述两道题目的求解中,将已知式或所求式的分母视为1,逆用1＝sin2α＋cos2α进行等价代换,实现了已知与未知之间的转化,从而使问题简捷获解．另外需要注意的是在解含tanα的一元二次方程后,若得到两个解,该如何取舍?本题由cosα＋可知α在第三象限,从而tanα只能取正数．

3 变形应用

例3已知,则角α所在的象限为( )．

A．第一象限 B．第二象限

C．第三象限D．第四象限

解析

将sin2α＋cos2α＝1两边同时除以cos2α,得；将sin2α＋cos2α＝1两边同时除以sin2α,得．所以

进而可判断出当α在第四象限时,有

故选D．

变式证明如下两个等式：

(2)由1＝sin2α＋cos2α,得1－sin2α＝cos2α,即(1＋sinα)(1－sinα)＝cos2α．

由已知可得1－sinα≠0,cosα≠0,所以

点评

上述两道题目的解答均借助了同角关系的变形应用．类似地,由1＝sin2α＋cos2α变形还可得到0)．在同角关系变形应用中,可变的形式还有很多,同学们可自行探究．

“学以致用”是学生学习的主要目标,公式的应用包括3个方面,即正用、逆用和变形用．在具体问题的求解中,如何灵活应用同角关系,关键在于对所给条件与所求结论的准确识别,将其与同角关系建立关联．对于明显的关联,可直接利用同角关系进行求解；对于较为隐含的关联,可通过转化后,再建立关联,转化的方向基于平时学习的积累与总结．本文中所列举的几类问题,形异但质同,万变不离其宗,求解过程中均体现了同角关系的正用、逆用或变形用．