向心球轴承载荷分布分析及寿命计算

李其宸，赵礼辉，付道琪

（200093 上海市 上海理工大学 机械工程学院）

0 引言

向心球轴承广泛用于各类机械设备中，能够承受径向载荷和一定的轴向载荷，具有结构简单、制造精度高和摩擦系数小等优点[1]。在大多数应用场合中，可以仅考虑部分主要载荷，如径向载荷、轴向载荷或轴向载荷与径向载荷共同作用下联合的负荷，而当有很重的载荷作用时，安装在轴承上的轴就会发生弯曲，从而在轴承上产生一个不可忽视的弯矩载荷。在联合载荷作用下，轴承中滚动体的载荷分布将发生显著变化，它们将引起轴承位移、接触应力和疲劳寿命的显著改变。

作用在轴承上的负荷由滚动体通过一个套圈传递到另一个套圈，大多数情况下，轴承内部各滚动体所受到的负荷是不同的，负荷的大小、滚动体与套圈之间的接触应力和循环次数都会直接影响轴承的性能和寿命[2-3]。

针对轴承接触载荷的计算求解主要有3 类方法，包括有限元、数值仿真以及试验3 类方法。本文考虑轴承接触角的变化，基于拟静力法建立向心球轴承在承受径向、轴向以及较小弯矩联合载荷作用下的力学平衡方程，研究了不同载荷对载荷分布的影响，并以此为基础结合轴承额定寿命理论研究了不同载荷疲劳寿命的影响。

1 建立数学模型

1.1 变形与负荷关系

球轴承的滚动体与套圈接触处的变形量与负荷关系为

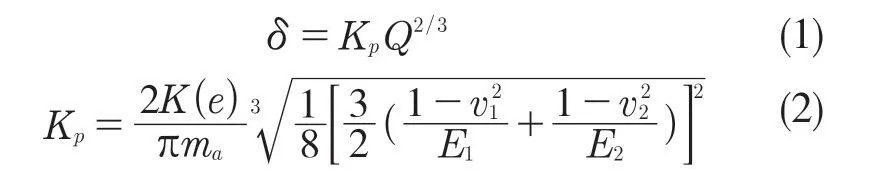
式中：v1，v2——轴承滚珠和套圈材料的泊松比；E1，E2——轴承滚珠和套圈材料的弹性模型；——系数，可通过计算主曲率函数Fρ查表得到。

轴承的主曲率函数定义为

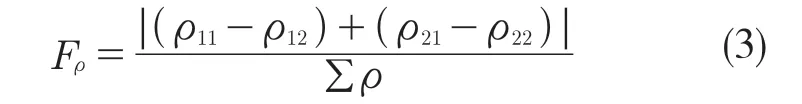
钢球在接触点处的主曲率为

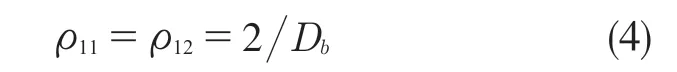
套圈在接触点处的主曲率分别为

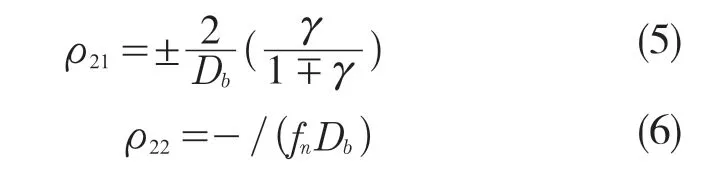
每一个主曲率有2 个数字下角标，第1 个下角标表示所指的物体，第2 个下角标表示物体所在的主平面。式（5）中的正号代表内圈，负号代表外圈。

其中，γ为轴承结构参数

fn为滚道沟曲率半径系数

式中：rn——滚道沟曲率半径，其中n=i、e，分别代表轴承的内圈、外圈；Db——轴承滚珠的直径；Dm——轴承平均直径。

1.2 接触角变化的考虑

轴承实际工作时，滚珠与套圈之间的接触角不是一个固定值，而是不断变化的，且每个滚珠与套圈之间的接触角是不同的。初始状态时，轴承滚珠与内外圈的接触角相等。如图1 所示，α0为初始接触角，受轴向负荷后，内外套圈沿轴向有相对趋近量δa，此时实际接触角为α。

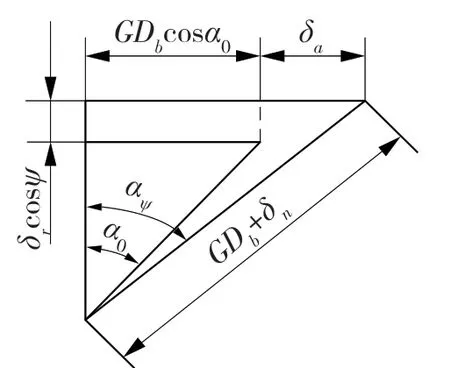
图1 向心球轴承的接触角Fig.1 Contact angle of centripetal ball bearing

由图1 可得内外沟曲率中心之间的距离为

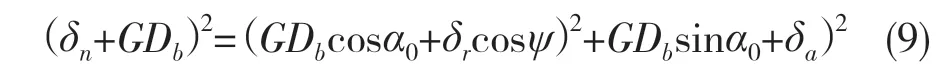
式中：G=fe+fi-1。

由图1 可得任意角位置ψ处

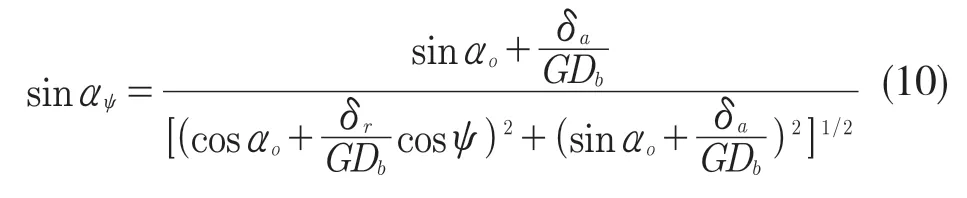
式中：δψ——轴承不同角位置处的实际接触角。

1.3 受径向、轴向和弯矩联合负荷的轴承

轴承同时承受径向负荷、轴向负荷和弯矩时，内外圈会产生相对位移，包括轴向位移δa、径向位移δr和相对倾角θ。如图2 所示，假设外圈固定，轴承受负荷后，内圈相对于外圈产生相对位移。

轴承受负荷后，内圈滚道沟曲率中心所在的圆周半径为

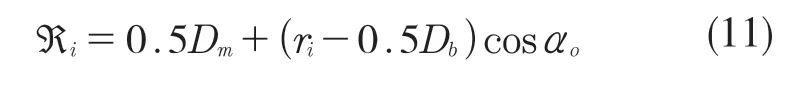
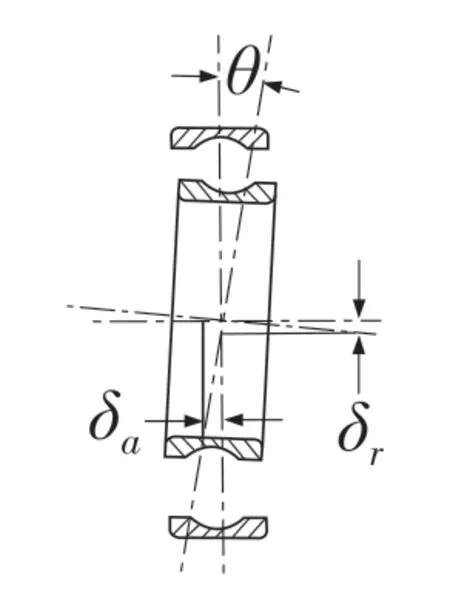
图2 联合负荷下的内圈位移Fig.2 Inner ring displacement under combined load

外圈滚道沟曲率中心所在的圆周半径为

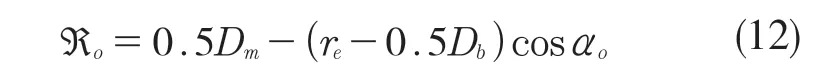
在任意角位置ψ处，内外套圈沟曲率中心间的距离为：

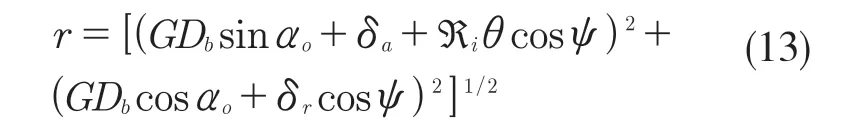
引入无量纲量

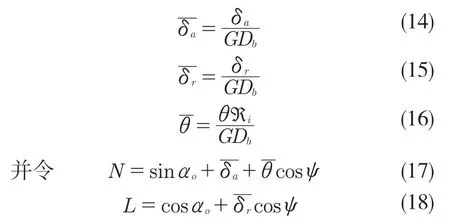
将式（17）、式（18）带入式（13）得

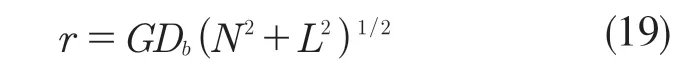
角位置ψ处钢球与内外套圈接触得到总的变形量为

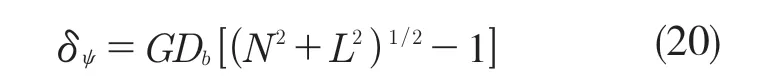
根据式（1），轴承的接触负荷为

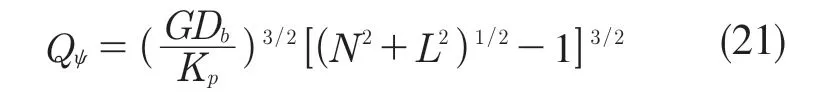
此时，任意角位置处钢球与套圈的接触角为

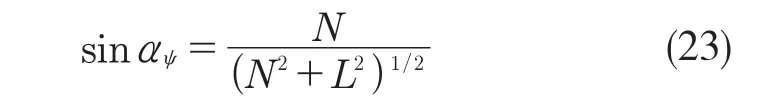
根据平衡条件，若作用于轴承得径向负荷、轴向负荷和弯矩分别Fr，Fa和M，则有

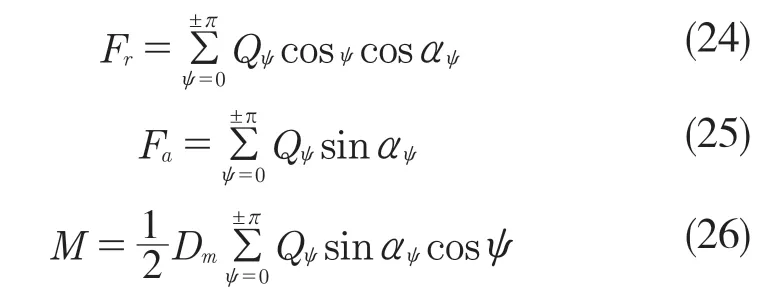
2 轴承寿命计算模型

目前的工程应用中，轴承制造商普遍接受的是基于Lundberg-Palmgren 轴承寿命理论改进的ISO 标准，ISO 标准需要计算轴承的当量等效动载荷与额定静载荷。根据轴承额定寿命理论，球轴承的额定寿命为

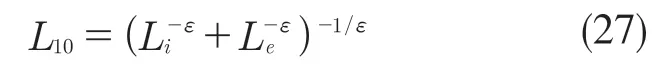
内滚道的额定寿命为

外滚道的额定寿命为

式中：Qcμj，Qcvj——套圈的额定静载荷。

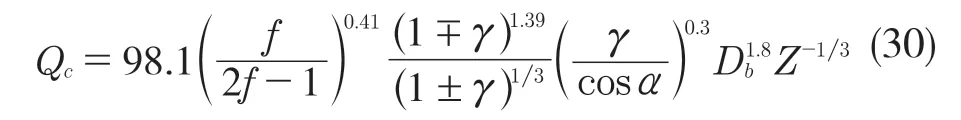
式中：∓——内、外圈的额定动载荷。

旋转内滚道的当量动载荷Qμi为

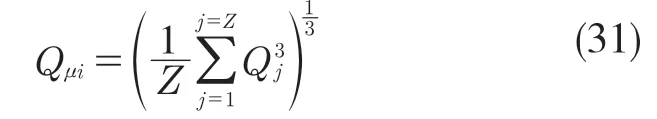
非旋转外滚道的当量动载荷Qvj为

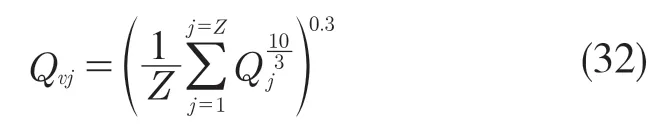
式中：j——轴承滚珠的编号；Z——滚珠的总数量。

3 计算结果研究与分析

接触载荷是轴承静力分析的重要内容，与轴承的疲劳寿命、功率损耗以及接触应力有关，因此有必要对轴承的接触载荷进行评估。本文以6007 型号向心球轴承为例进行分析验证，轴承几何参数见表1。

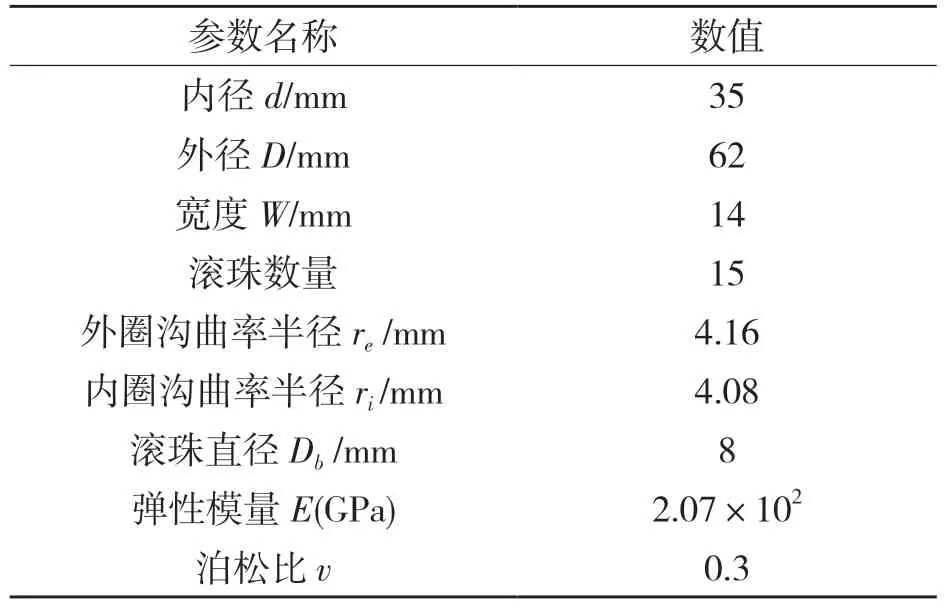
表1 轴承参数Tab.1 Bearing parameters

3.1 载荷分布分析

如图3 所示，计算了滚动体的最大接触载荷，轴承工作条件为：径向载荷Fr=2 000 N，轴向载荷Fa=3 000 N，弯矩M=20 N·m。横坐标为轴承滚子的编号，纵坐标为滚子最大接触载荷，在联合负荷作用下，滚子最大接触载荷达到了818 N。

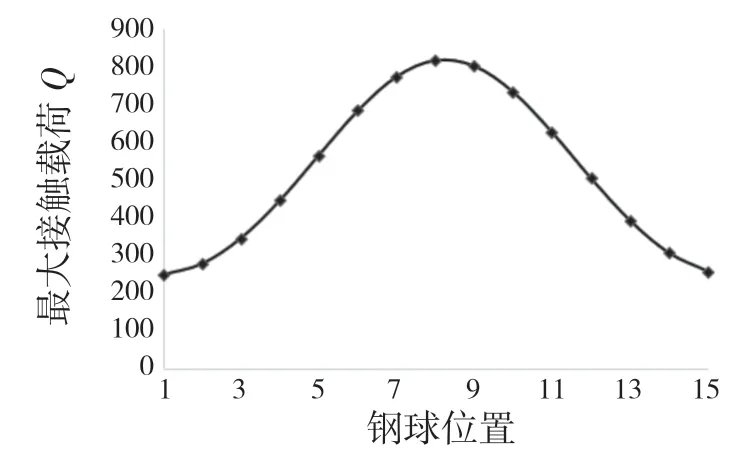
图3 联合负荷作用下滚动体的最大接触载荷Fig.3 Maximum contact load of rolling body under combined load

实际工作接触角如图4 所示，接触载荷的增加导致接触角变大，实际工作接触角的变化趋势与滚动体接触载荷的变化趋势保持一致，且与文献[5-6]中的数值结果分布一致，表明了数值迭代结果的合理性。

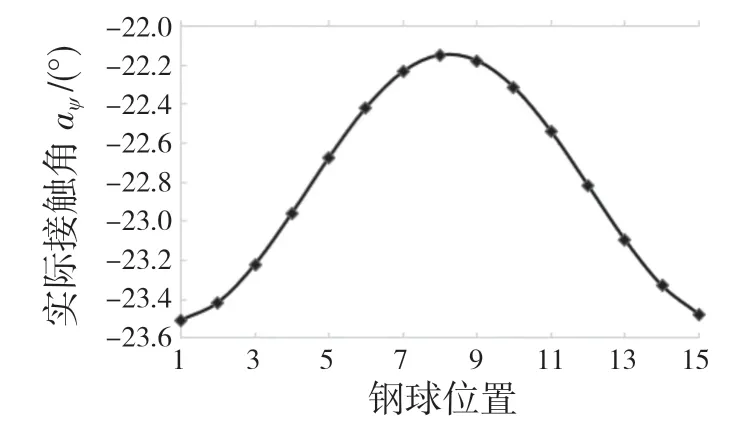
图4 实际工作接触角Fig.4 Actual working contact angle

3.1.1 径向载荷对载荷分布的影响

由图5 可以看出：（1）随着径向载荷的增加，钢球最大接触载荷增大，若径向载荷持续增加，则会出现仅有几个滚动体承受负荷，导致轴承的载荷分布不均匀现象；（2）径向载荷减小，钢球的最大接触载荷减小，载荷分布区域增加，但轴承内部钢球接触载荷分布更加均匀。

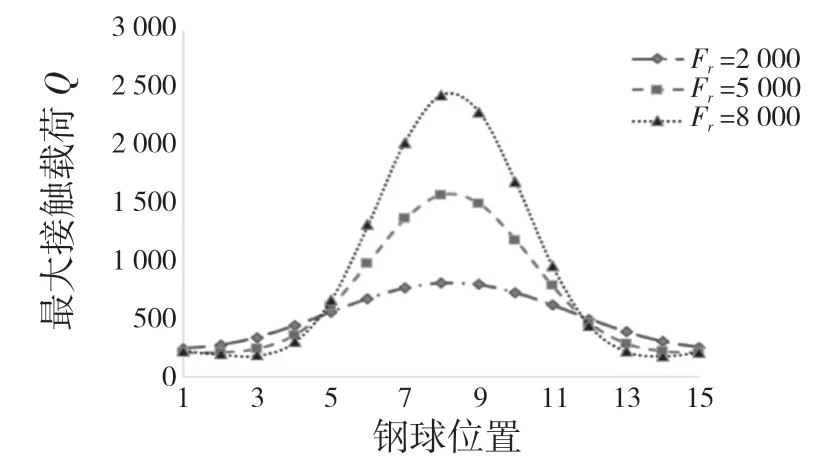
图5 径向载荷对载荷分布的影响Fig.5 Effect of radial load on load distribution

3.1.2 轴向载荷对载荷分布的影响

由图6 和图7 可以看出：（1）轴向载荷增加，钢球的最大接触载荷显著增大，载荷分布区域也变大，这是因为轴向载荷的增加导致接触角的变大，轴承接触角越大，使得载荷分布更加均匀，轴承的承载能力越高；（2）轴向载荷减小，钢球最大接触载荷减小，受载较小的钢球位置接触角显著减小，部分滚子脱离滚道接触，载荷分布区域也变小，容易导致应力集中现象。

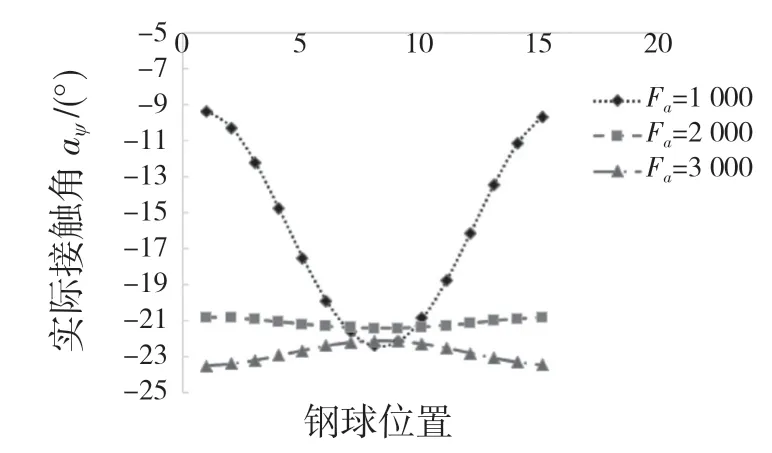
图7 轴向载荷对接触角的影响Fig.7 Effect of axial load on contact angle

3.1.3 弯矩对载荷分布的影响

由图8 和图9 可以看出：

（1）弯矩增加，钢球最大接触载荷增大，接触区域显著，且逐步呈对称分布。弯矩使得轴承的内、外圈之间发生倾斜，产生相对倾斜角θ，导致轴承内部载荷的分布的变化。

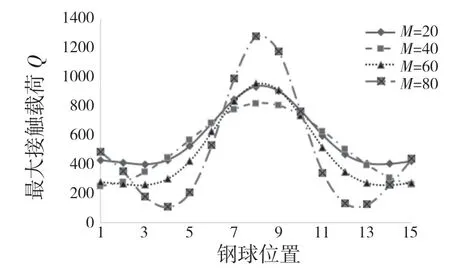
图8 弯矩对载荷分布的影响Fig.8 Effect of bending moment on load distribution

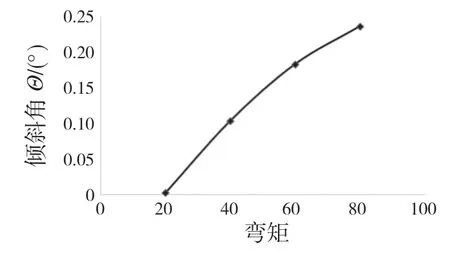
图9 弯矩对倾斜角的影响Fig.9 Effect of bending moment on tilt angle

（2）尽管弯矩的增加直接导致接触载荷变大，但较小的弯矩载荷可以消除滚子歪斜导致的应力集中现象，使轴承内部钢球接触载荷分布更加均匀。

3.2 载荷分布对轴承寿命的影响

3.2.1 径向载荷对轴承疲劳寿命的影响

由图10 可知，径向载荷增加，钢球的最大接触载荷变大，载荷分布区域减小，轴承的疲劳寿命急剧减小。

图10 径向载荷对轴承疲劳寿命的影响Fig.10 Effect of radial load on bearing fatigue life

3.2.2 轴向载荷分布对轴承疲劳寿命的影响

根据图11 可知，在较小的载荷范围内，轴向载荷增加，轴承的疲劳寿命减小；但随着轴向载荷继续变大，轴承的疲劳寿命变化幅度降低。

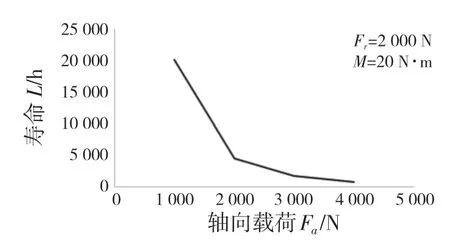
图11 轴向载荷对轴承疲劳寿命的影响Fig.11 Effect of axial load on bearing fatigue life

3.2.3 弯矩对轴承疲劳寿命的影响

根据图12 可以看出，轴承在弯矩载荷作用下，内外圈之间产生相对倾斜，显著降低轴承的疲劳寿命，这是滚动体的接触载荷增加导致的；但较小的弯矩可以消除载荷不稳定产生的其他附加弯矩，改善轴承的疲劳寿命。

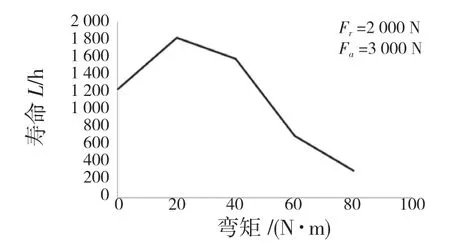
图12 弯矩对轴承疲劳寿命的影响Fig.12 Influence of bending moment on bearing fatigue life

4 结论

本文建立了向心球轴承的力学行为模型，同时考虑轴承实际工作接触角的变化，根据轴承滚动体的变形与接触载荷之间的变形协调关系模拟计算过程，得到轴承在联合负荷下的轴承滚动体接触载荷分布状态，研究了不同的载荷参数对接触载荷分布以及轴承疲劳寿命影响的规律。结果表明，径向载荷、轴向载荷以及弯矩均能显著影响轴承的疲劳寿命；轴向载荷增加时，接触角变大，能够提高轴承的承载能力，较小的弯矩载荷可以改善轴承的疲劳寿命。